平头锥型回转体高速入水结构强度数值分析*

黄志刚，孙铁志，杨碧野，张桂勇,2,3，宗 智,2,3

（1.大连理工大学船舶工程学院辽宁省深海浮动结构工程实验室，辽宁 大连 116024；2.大连理工大学工业装备结构分析国家重点实验室，辽宁 大连 116024；3.高新船舶与深海开发装备协同创新中心，上海 200240）

回转体从空中高速跨越空气和水交界面时，受到水介质对其作用的巨大冲击载荷，从而引起回转体发生形变和破坏，这就需要设计的回转体强度满足结构安全要求。同时由于回转体入水过程涉及气-液-固三相耦合作用[1]，在高速条件下这种流固耦合作用变得更复杂，从而大大增加了研究高速回转体入水问题的难度。因此，开展回转体高速入水过程结构强度研究对回转体结构设计具有重要意义。

入水问题研究长期以来一直受到广泛关注。最早Worthington等[2]利用闪光摄影技术，观测到了小球落水时的液体飞溅和空泡现象。在理论研究上，1929年，Von Karman[3]最早提出使用附加质量法计算了入水冲击载荷，并采用动量守恒定律推导了相关的计算公式。随后Wagner[4]在此基础上运用伯努利方程，提出了平板理论，此理论在研究结构入水过程受力和流体动能方面得到了广泛应用。Mayo[5]考虑了波浪对附加质量、压力分布、入水冲击载荷的影响。May[6]研究了导弹在垂直和倾斜入水过程中的入水空泡形成、发展和溃灭的过程，同时研究了入水过程的流场变化情况。近些年来，随着数值计算能力的提高，有限元将流体和结构耦合解决了大型三维几何入水问题。Anghileri等[7]利用有限元分析了刚性球在垂直入水过程中所受的载荷。Faltinsen等[8]建立了入水问题的数值和理论模型，并通过相关的入水实验验证其模型的准确性。Korobkin等[9]运用边界元和有限差分法计算悬浮体入水冲击过程中引起的液流非定常问题。Donguy等[10]对二维、三维、刚性和弹性体的入水耦合过程进行了详细分析，其采用的是一种变化的有限元耦合方法，通过耦合矩阵处理流体和结构之间的作用。

郑金伟等[11]利用LS-DYNA程序计算了三维刚体结构倾斜入水过程的流体压力和冲击载荷。施红辉等[12]、Shi等[13]通过钝体入水实验测量了水下声场的变化，获得了激波的空间能量分布以及传播速度变化，同时其还研究了钝体入水自由液面变形问题和超空泡现象。王云等[14]开展了模型实验，利用高速摄像机拍摄了回转体入水过程的空泡形态演变，分析了头型、入水角度、入水速度和水下弹道的影响。潘光等[15]利用MSC.DYTRAN软件计算了入水过程中鱼雷所受到的冲击压力以及压力分布情况。黄凯等[16]通过实验研究了回转体头型对反弹水花的影响，发现回转体顶角越大，空泡越大。李佳川等[17]基于入水弹道学和超空泡理论，研究了不同扰动角速度下的回转体入水轨迹、速度、俯仰角的变化。张伟等[18]、郭子涛等[19]开展了水平回转体入水实验，研究了回转体入水过程的弹道稳定性和空泡拓展特性，计算了入水阻力系数，并将实验中回转体的速度衰减曲线与理论解进行对比，两者吻合良好。马庆鹏等[20]通过球体入水实验，分析了球体入水过程中的入水空泡演变过程，得到了不同的入水速度以及表面黏湿状态对入水空泡流场的影响。

目前针对入水问题已开展了大量的研究，并取得了丰硕的成果，然而在研究回转体速度达到100 m/s及以上的高速入水问题时，多以入水空泡演化以及回转体入水稳定性作为研究重点。由于高速入水问题是冲击作用时间极短的非线性问题，对高速回转体入水过程结构强度方面的研究仍显不足。本文中采用数值计算的方法，分析入水过程中的冲击载荷特点，并开展回转体在不同壳体厚度情况下高速入水过程结构强度研究，以期获得的研究成果可为高速回转体模型结构设计提供参考，同时丰富入水过程机理内涵。

1 数值计算模型设置

1.1 流固耦合ALE算法及状态方程

基于LS-DYNA通用非线性有限元程序，使用ALE(arbitrary Lagrangian-Eulerian)方法模拟回转体入水，计算入水冲击载荷、平均压力以及速度等的变化，着重考虑此过程中回转体的形变情况。

在计算中，首先进行Lagrange时步计算，单元网格随材料流动开始变形，然后进行ALE时步计算：

(1) 保持变形后物体边界条件不变，内部单元进行重分网格，称为光滑步。

(2) 变形后的网格中的单元变量（密度、能量、应力张量等）和节点速度矢量输运到重新划分的新网格中，称为对流步。

在LS-DYNA中，流体介质的压力由状态方程进行描述，本文中研究三维回转体-水-空气相互耦合求解过程。对于空气和水，采用LS-DYNA中的NULL材料，对空气介质压力，使用多项式状态方程描述，在LS-DYNA中通过*EOS_LINEAR_POLYNOMIAL关键字施加，状态方程压力公式用下式表示：

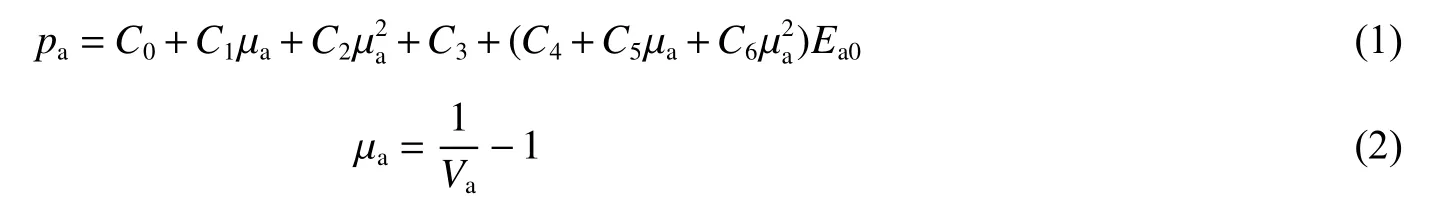
式中：pa为气体压力，C0～C6为自定义常数，Va为相对体积， µa为体积变化率。对理想气体，C0～C3、C6均为0，C4=C5=γa-1， 其中 γa为单位热值率,初始气体内能Ea0=253.3 kJ

对于水介质，其压力使用Grüneisen状态方程描述，在LS-DYNA中所使用的关键字为*EOS_Grüneisen，水压力方程表示为：

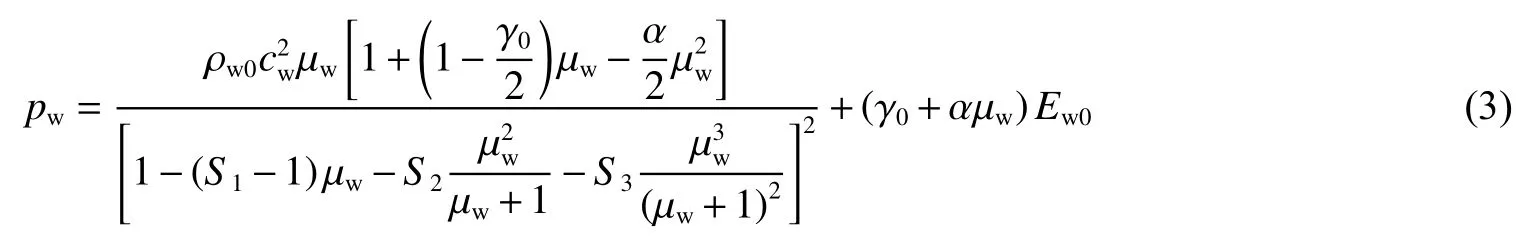
式中：pw为水压力，cw为声音在水中的传播速度， µw为体积变化率，α为对Grüneisen系数 γ0的一阶体积修正，S1、S2、S3分别为us-up曲线斜率无量纲系数，us为冲击波速度，up为流体质点的速度，Ew0为材料初始内能。模拟中水状态方程参数：cw=1 647 m/s，S1=1.921，S2=-0.096,S3=0， γ0=0.35，Ew0=289.5 kJ，相对初始体积Vw0=1.0。

1.2 计算模型及网格划分

建立计算域模型如图1所示，计算域包括空气域和水域。空气域尺寸为1.2 m×1.2 m×1.0 m，水域尺寸为1.2 m×1.2 m×1.5 m。水域和空气域宽度为回转体最大直径的10倍。在模拟中采用了2种回转体,其结构形式分别为：(1)全回转体等厚度；(b)回转体头部部分厚度为8 mm，后体区域赋予一种厚度。回转体模型整体为平头锥形结构，最大直径为120 mm，头部直径为100 mm，回转体长度为0.508 m，其首端倾斜斜面与回转体头部平面所呈角度为104.7°，回转体外形如图2所示。

图1 计算域Fig.1 Computational domain

图2 回转体几何模型Fig.2 The geometrical model for a revolution body

在模型单元类型的选择上，弹壳体采用4节点SHELL单元，水和空气采用单元类型为LS-DYNA中模拟ALE物质的SOLID_ALE六面体单元。在入水的初始时刻保证回转体在空气中垂直水面向下，头部贴近水面位置。模拟中应用了ALE多物质算法，空气和水为2种ALE物质。结构和流体通过*CONSTRAINED_LAGRANGE_IN_SOLID进行耦合，同时使用*INITIAL_FRACTION_GEOMETRY关键字将回转体的内部物质设置为空气，这样符合实际情况，模拟更准确。

由于高速入水过程时间极短，重力对整个入水过程的影响很小，所以在模拟中忽略重力的作用。

在数值计算过程中，回转体为弹塑性材料，外壳采用45钢材，四边形网格大小为0.005 m。水和空气六面体网格大小为0.02 m，计算模拟中总网格量为520 000。45钢材的密度为7 850 kg/m3，杨氏模量为210 GPa，泊松比为0.3，屈服应力为355 MPa，塑性失效应变为0.35。

2 计算结果与分析

2.1 数值方法验证

为了验证数值方法的准确性，选取第1种工况下板厚为5 mm的回转体进行入水计算。在入水的瞬间回转体头部会受到巨大的冲击载荷，其中心区域有最大的压强峰值。通过数值模拟得到的回转体中心区域在入水抨击过程中的压强曲线，如图3所示，其抨击压强的最大值为189 MPa。参考王珂等[21]对弹性回转体入水抨击载荷峰值的预报，弹性回转体入水抨击压强峰值与回转体的厚度、入水速度以及材料的弹性模量有关，抨击过程峰值压强p可以表示为：

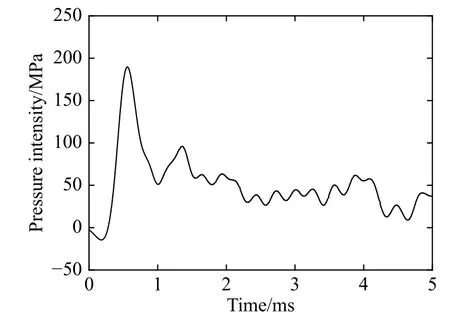
图3 回转体头部中心区域压强曲线Fig.3 Pressure intensity curve in the central head region of the revolution body

式中：kd=0.00423d2+0.003758d+0.42，kE=ln(E/Pa)+15，kv=+5； ρw为水的密度；kd为厚度相关系数，d为回转体厚度(m)；kE为弹性模量相关系数，E为材料弹性模量；kv为速度相关系数，v0为回转体入水的初速度(m/s)。由式(4)可以求得在5 mm板厚下的回转体入水冲击载荷压强峰值为173 MPa，和本文求得的数值解比较接近，但数值模拟结果略大于公式求得的抨击压强峰值。其原因是在数值模拟中未考虑空气垫的作用，即高速时的空气压缩效应，这也在一定程度上解释了数值模拟所得压强数值偏大的现象，空气垫效应是数值模拟过程中较难考虑的一个因素，在数值模拟方面还有很大的研究空间，亟待将来的研究。

除将入水时回转体头部抨击压力的峰值与拟合公式相对比外，还进行了回转体入水过程中速度衰减的对比验证，为了更好地对比速度衰减过程，在此数值模拟中延长了入水过程的求解时间，增大水域深度至3.5 m，计算时间为0.11 s。参考文献[18]，根据牛顿第二定律，忽略重力效应。

假定回转体在入水过程中空泡内外压差保持不变，同时空化数为非定值，有：

式中：Δp为回转体入水空泡内外压差， ρa和 ρw分别为空气和水的密度，v0为回转体入水初速度，vp为回转体在水中的速度；Ca为气流压力降因数，Ca=5～15； σ0为初始空化数，σ0=0.006～0.018。

柱形平头回转体阻力因数和空化数关系式：

忽略入水过程中重力的影响，回转体有以下运动方程：

式中：mp为回转体的质量，A0为回转体头部面积。

根据式(5)～(6)得到速度衰减和时间的关系式：

式中：衰减系数k=ρwA0Cp/2mp。依据式(8)计算回转体入水速度衰减曲线并与数值模拟结果进行对比，如图4所示。从图4可以看出，数值模拟结果与理论速度衰减曲线吻合较好，从而进一步验证了所建立的数值方法的有效性。

图4 回转体速度衰减曲线Fig.4 Velocity attenuation of the revolution body over time

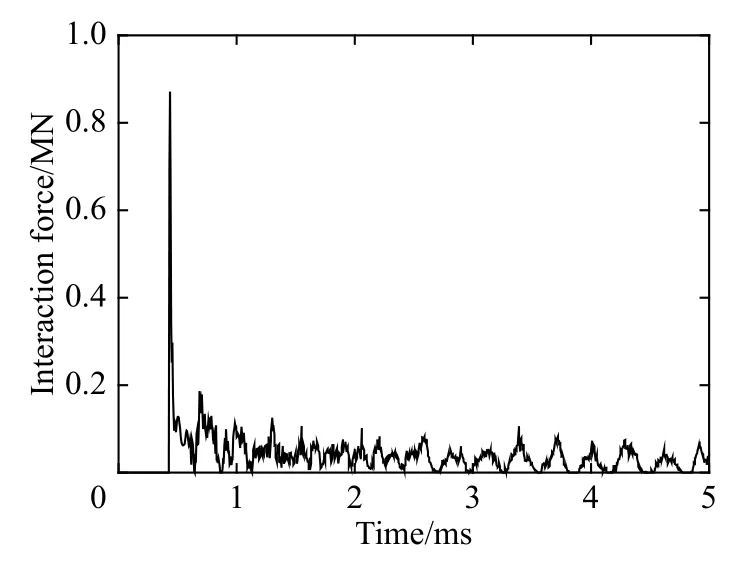
图5 流-构耦合力曲线Fig.5 Fluid-structure interaction force varying with time

在入水数值验证工作的同时，图5给出了当前回转体结构形式下入水过程中回转体头部表面作用力曲线图，可以进一步分析回转体入水过程受力特征。从图5可以看出，回转体头部受到的作用力在入水瞬间急剧上升，达到峰值后迅速下降，最后以小幅度震荡趋势变化。可见在入水瞬间产生了巨大冲击力，所以在设计回转体模型时要重点考虑入水瞬间的结构强度。下面将对2种结构形式的回转体进行强度的分析计算。

2.2 全回转体等厚度工况模拟

在模拟中，首先进行回转体等厚度工况分析，分别计算回转体厚度为2、3、4和5 mm的情况。计算中发现：只有回转体厚度为5 mm时，该种结构的回转体是安全的；此种结构的回转体发生破坏时，破坏部位均发生在回转体头部和锥形斜面连接处。对回转体厚度为2 mm的计算结果进行分析，其中1.1 ms和3.0 ms时刻的应力云图分别如图6和图7所示。由图6～7可以清晰地看出，破坏部位为头部和锥形斜面连接处，回转体头部中心处未发生破坏现象。提取回转体头部和锥形斜面连接处的塑性应变和单元应力曲线，分别如图8和图9所示。由这2条曲线可以得到：在回转体入水过程中，等效应力达到了材料的屈服应力355 MPa，塑性应变也达到了材料的塑性失效应变0.35，因此回转体出现破坏现象。可见，回转体头部和锥形斜面连接处应予以加强，来承受入水瞬间高数量级的冲击载荷。同时因为入水过程中回转体头部为主要的冲击载荷作用面，所以对回转体头部进行加强是十分必要的。

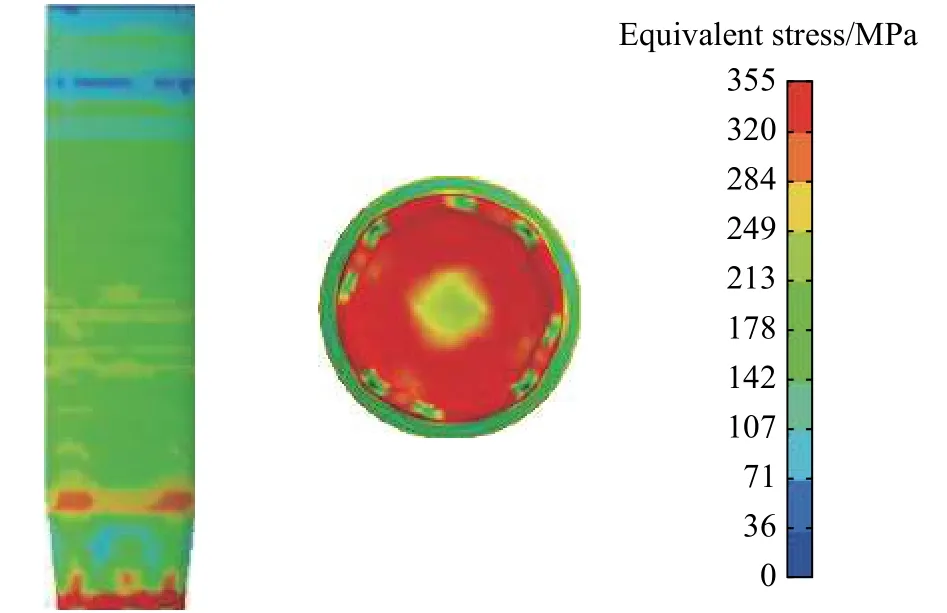
图6 在t=1.1 ms时回转体的应力分布Fig.6 Stress distribution in the revolution body at t=1.1 ms

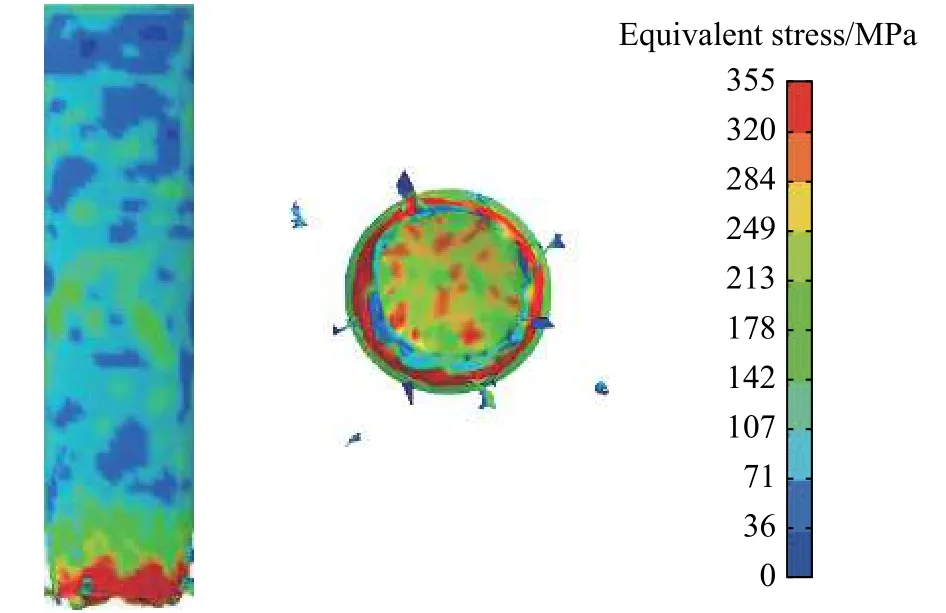
图7 在t=3.0 ms时回转体的应力分布Fig.7 Stress distribution in the revolution body at t=3.0 ms

图8 回转体头部边缘单元应变曲线Fig.8 Strain-time curve of the edge element for the head of the revolution body

图9 回转体头部边缘单元等效应力曲线Fig.9 Equivalent stress-time curve of the edge element for the head of the revolution body

2.3 回转体头部壁厚的影响

由2.2节中计算结果可知，回转体头部和锥形斜面连接处强度脆弱，因此对回转体头部进行加强，考虑到工程安全系数要求，将头部赋予8 mm的厚度，回转体其余板厚度分别赋予2.0、2.5、3.0、3.5和4.0 mm。在初速度相同的条件下分别进行计算，由计算结果可知：在头部厚度为8 mm、后体区域厚度为2.0 mm时，回转体无法满足强度要求；在后体区域厚度为2.5 mm及以上时，结构强度满足要求。选取后体区域厚度为2.5 mm的情况加以分析。回转体入水过程中0.89 ms和2.00 ms时刻的应力云图分别如图10和图11所示，同时图12给出了回转体头部边缘和头部中心单元塑性应变曲线，图13和图14分别给出了回转体头部和头部中心单元的等效应力变化曲线。由应力、应变变化曲线可知，在回转体入水过程中，无论其边缘还是中心单元的等效应力很快达到屈服应力355 MPa，随后等效应力下降并表现为波动变化。回转体头部边缘的塑性应变由0迅速到达0.14，并最终趋近0.16，回转体头部中心的塑性应变有同样的变化规律并最终达到0.25。这个塑性应变小于材料的塑性失效应变0.35，因此，材料虽然进入塑性阶段，但还未达到破坏，此时回转体结构满足强度要求。

图10 t=0.89 ms时刻回转体的应力分布Fig.10 Stress distribution in the revolution body at t=0.89 ms

图11 t=2.00 ms回转体应力图Fig.11 Stress distribution in the revolution body at t=2.00 ms

图12 回转体头部边缘及中心单元应变随时间的变化Fig.12 Strain-time curves of the edge and central elements for the head of the revolution body

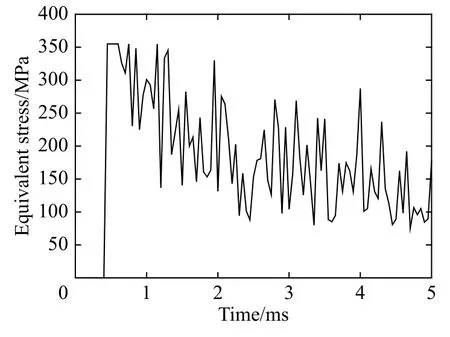
图13 回转体头部边缘单元等效应力曲线Fig.13 Equivalent stress-time curve of the edge element for the head of the revolution body

图14 回转体头部中心单元等效应力曲线Fig.14 Equivalent stress-time curve of the central element for the head of the revolution body

3 结 论

采用有限元方法对平头锥头回转体在高速入水过程中的结构强度进行了数值分析，得到的主要结论如下：

(1) 在回转体入水的瞬间，其头部受到高速冲击载荷，且作用时间极短，在研究回转体高速入水时要重点考虑入水瞬间的作用力。

(2) 在回转体等厚度结构形式下，等效应力和塑性应变均较大，在入水初速度为100 m/s、回转体厚度小于5.0 mm时，回转体应力达到了材料的屈服应力355 MPa，其塑性应变也达到失效应变0.35，此种形式下回转体厚度低于5.0 mm时无法保证回转体的强度要求。

(3) 当回转体入水初速度为100 m/s、其头部厚度为8 mm、其后体壁厚为2.5 mm及以上时，结构未发生破坏，此时回转体可以满足强度要求，但材料同样进入了塑性阶段，建议对实际结构还应该考虑一定的安全系数。