基于改进MP-WVD算法的核电厂建设爆破振动信号处理方法*

梅 比，汪旭光，杨仁树

（1.中国矿业大学（北京）力学与建筑工程学院，北京 100083；2.北京矿冶研究总院，北京 100160）

我国核电建设进入加速期，由于核电站规模较大，无法多机组同时建设，因此在后期机组施工时就要考虑到已建机组的安全稳定，尤其是爆破施工产生的振动影响[1]。研究表明，建（构）筑物在地震波作用下产生的动力响应特征与波的时频能量特性密切相关。目前时-频分析算法有各自优缺点：STFT算法(short-time Fourier transform)最初为傅里叶变换应用于时频分析提供了可能，但是郭涛等[2]通过对传统的STFT算法与小波算法进行对比分析得到了传统的STFT以三角函数作为基函数，无法准确与爆破振动这种非稳态随机过程相匹配的结论。马华原等[3]将小波变化方法运用于核电施工爆破振动分析取得了良好的效果，但也发现小波变换虽然引入了更加适配的小波基，但时频分辨率受测不准原理限制。李夕兵等[4]、魏新江等[5]改进了HHT算法(Hilbert-Huang transform)并将其运用于爆炸振动分析中，获得了具有比小波变换分辨率更高的时频分布图谱。但随着研究的深入，HHT变换提出的自适应基底导致算法边界效应较大，这一点目前仍是个难题。另一方面，周辉等[6]对传统的匹配追踪算法进行了改进，提供了消除经典WVD算法(Wigner-Ville distribution)交叉干扰项的思路，在此基础上，本文将改进型MP算法(matching pursuit algorithm)与传统WVD算法相结合，成功解决了交叉项干扰的问题，同时很好地控制了算法的计算复杂度。结合核电爆破信号实例，取得了较好的分析效果。

1 算法基本原理概述

1.1 WVD分布

WVD算法最初是由Ville将其应用到信号的时-频分析领域的[7]，针对一个时间序列W(t,ω)根据特征函数方法推导出WVD表达式：

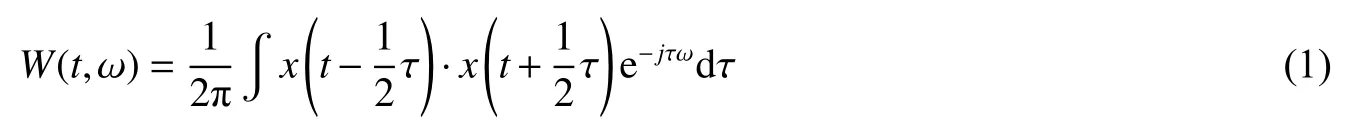
式中，t为时间，ω为角频率。由式(1)可知，在信号WVD表达中，不存在任何形式的窗函数。因此，WVD分相对STFT、小波变换而言有着更高的时间和频率分辨率灵活性。

1.2 MP算法

MP算法是由Mallat于1993年提出的一种信号分解算法[8]。其核心原理是将信号以字典原子为基，进行分解。过程如图1所示：选取与信号Xn匹配程度最高的原子Ψn，并求出投影值an和差值信号Xn+1。此时得到残差信号Xn+1，重复进行原子匹配过程，将其投影到与其最相近的原子Ψn+1上，得到差值信号Xn+2。以此类推，直到残余信号的能量小于设定的阈值为止。

MP算法是一种贪婪算法，该方法与统计学中使用的投影追踪算法和波形增益矢量量化有密切关系。信号的分解需要在超完备子波库中进行，其中，超完备意为信号的分解目标在信号所组成的空间中足够密集，这也就是最终无法以一组正交基进行描述。对于任意一个有限维 Hilbert 空间H，D为此空间内的一个超完备词典，设信号为f∈H，长度为N，D中的元素满足：

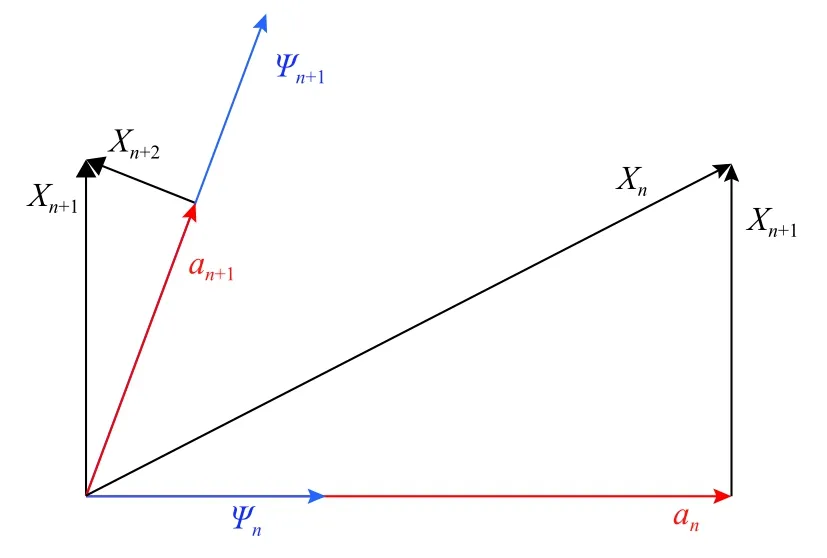
图1 分解过程示意图Fig.1 Schematic diagram of decomposition process

式中：gγ为子波分解算子，Γ为伽马函数。

MP算法就是将信号f垂直投影到子波库D的子波上。设则f可以表示为：

式中：Rf的意义为原始信号f通过子波匹配进行一次分解的残余[9]。为了达到最好的分解效果，就必须使残余信号尽可能小，因此就必然要使内积项取最大。很显然与Rf是正交的，因此：

设，经过了n次迭代(n>>0)得到残余信号=f此时再选择一个匹配子波使其匹配即：

就是进行了n+1次迭代得到的差值。因此MP算法即是利用式（5）描述的一个重复迭代过程，若迭代m次，则f可以表示为：

2 MP-WVD算法的缺陷及改进

WVD分布为非线性时频分布，也就是说其不具备线性分布的可加性，即两信号和的 WVD并不等于每一个信号的 WVD之和[10]。

令x(t)=x1(t)+x2(t)，则：

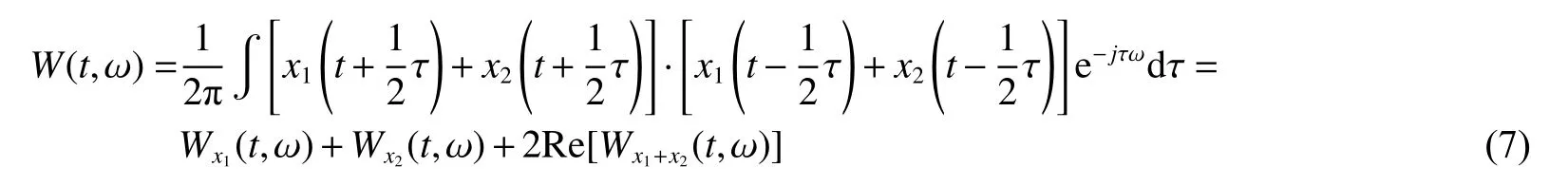
式中：2Re[Wx1+x2(t,ω)]是x1(t)和x2(t)的交叉项。t为时间，ω为角频率。

由式（7）可以看出，交叉项的存在对信号的时-频分布产生了很大的干扰。因此，将MP算法与WVD结合起来，将原始信号细分成基本原子，然后再对每个信号做WVD，将得到的结果叠加，在消除干扰项的基础上得到更清晰的时频分布图谱。具体示例如下。

示例信号x(t)，如图2所示。对示例信号x直接进行WVD运算，得到的时频分布情况如图3所示。可以看出图中不仅有4个真实分量的时频能量分布，还在任意2个分量的时频中心连线的中点处出现了交叉项，严重干扰了对信号真实时频分布的判读。

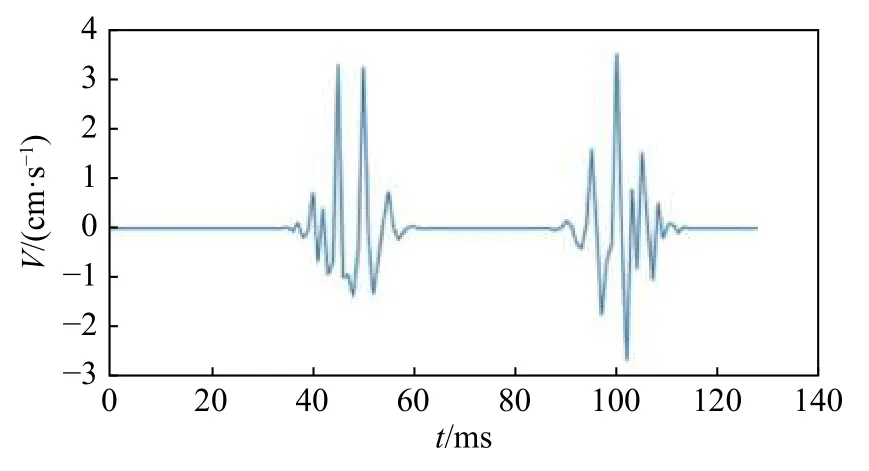
图2 示例信号x(t)Fig.2 Example signal x(t)

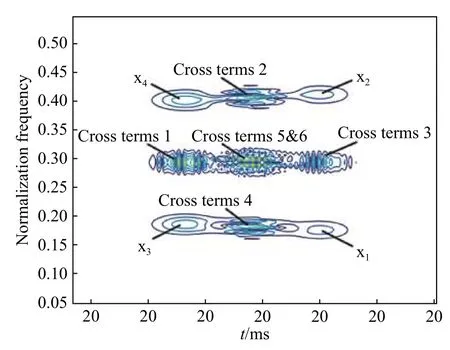
图3 WVD时频分布图Fig.3 WVD time-frequency distribution

现将示例信号x(t)代入MP算法，分解为x1、x2、x3、x4共 4个子项，如图4所示。

图4 MP算法分解结果Fig.4 Decomposition results of MP algorithm

再分别对4个子波进行WVD运算，得到其各自的WVD时频分布结果，如图5所示；将各子波的时频分布合并，即得到了原示例信号的时频分布情况，如图6所示。

可见，WVD变换在任意两个有效信号之间产生一个交叉项。图3中信号有4个分量共产生6个交叉项（其中交叉项5和6重叠），对N个分量则会产生N×(N-1)/2个交叉项 。而图4、5、6中采用MP子波分解方法，成功剔除了交叉项干扰。

另一方面，MP算法也存在着缺陷。其计算量过大，需耗费很长机时来完成一次信号分解[11]。而通常时频分析数据量都较大，因此研究者希望通过改进得到一种更高效的算法。

算法选用Gabor子项的控制参量有：振幅、频率、中心时间和相位[12]。对过完备子波库的扫描过程利用穷举法对这上述参量进行优化选择。引入HHT算法，通过EMD(empirical mode decomposition)分解得到信号的固有模态IMF(intrinsic mode function)分量。对IMF分量进行Hilbert变换，得到信号的瞬时优势频率以及相位，并将其代入MP算法中，即可将4参数扫描运算降维至2参数扫描，大大减少了程序循环步数。程序流程如图7所示。

与传统算法进行效率对比，分别用常规MP算法与改进后得MP算法对合成信号进行处理：

由表1中对比分析可以看出，经过改进后的算法效率有了明显提升，对同一信号分解所用机时有着50倍左右的差距。

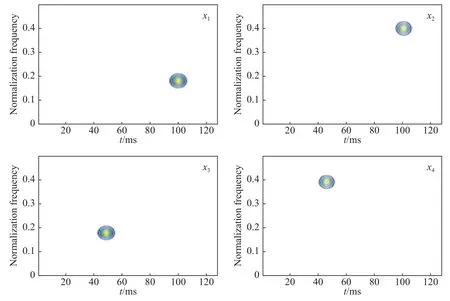
图5 各个子波的WVD分布Fig.5 WVD distribution of each wavelet

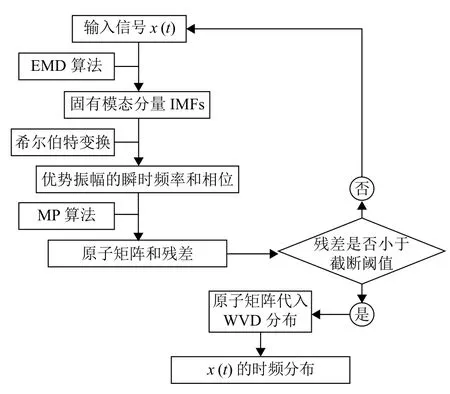
图7 程序框图Fig.7 Program diagram

表1 两种方法所用机时对比Table 1 Comparison of machine time between two methods

3 基于改进MP-WVD算法的核电爆破振动信号分析

3.1 工程概况

结合福建漳州核电厂一期工程场地平整土石方工程施工实例中监测到的爆破振动信号进行分析。本工程施工区域以5#、6#机组及其厂区西侧为界，功能设施为5#机组与6#机组主生产区和厂前区[13-14]。开挖后场平标高，13.5 m；土方量，603 200m3；石方量，5 878 300m3；回填方量，3 573 300 m3；挖沟槽土方，648 m3；石方，1 513 m3；边坡预裂面积，39 600 m2。

爆破振动监测点设置3个测点：人家村村委会东侧民房设置测点1，距离爆破施工位置859 m；南山村地标设置测点2，距离爆破施工位置678 m；水坝闸门设置测点3，距离爆破施工位置291 m。本文中选取三标段爆破实例，深孔爆破，采用乳化90炸药，其爆破技术参数如表2所示。

表2 爆破参数表Table 2 Blasting parameters

3.2 数据处理

以水坝闸门测点的振动信号的铅垂分量（Z轴）数据为例，利用改进MP-WVD算法进行分析。本次爆破振动测试采用了TC-4850型爆破测振仪，采样频率为10 000 Hz，采集到的典型爆破振动信号如图8所示。第一步做MP分解，所得到的子波集合如图9所示。分解得到的子波均具有良好紧支性[15]，可良好地呈现出信号的细节。

图8 原始信号Fig.8 Original signal

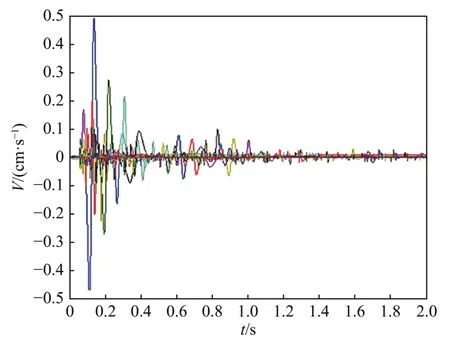
图9 子波集合Fig.9 Collection of wavelets

数据处理过程中发现，MP算法用于爆破振动信号高频去燥取得了十分理想的效果，与其他滤波算法进行对比研究，结果如图10所示。

从图10可看出，MP算法得到的重构信号保留了几乎所有的原始信号振动细节，同时剔除了高频噪声。小波变换得到的重构信号也能保持与原始信号的高度吻合，但有较大噪声残留，信噪比不如MP算法。EMD算法由于采用了自适应基底[16]，其算法速度非常快，但自适应基底导致滤波效果不稳定，容易将有用信息一同剔除；其边界效应也会引入多余信号，重构信号和原始信号差值较大。

将所得原子矩阵代入WVD算法，分别计算每个原子的时频分布，再逐一叠加，得到信号的总体时频分布如图11所示，基于小波变换的时频分析结果如图12所示。

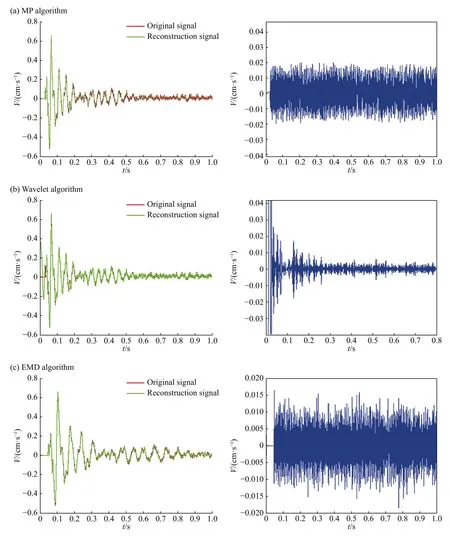
图10 滤波效果对比Fig.10 Comparison of filtering effects

由图12可知，小波变换结果不仅频率分辨率较低，且时间分辨率也不如MP-WVD算法得到结果，且存在一定的边界溢出问题。MP-WVD算法不仅有着较高的频率分辨率，同时较好地反映了地震波的频率分布随时间的变化而发生改变。从图11中可以清晰地分辨出此振动信号的特征：振动峰值在0.13 s左右到达，频率中心为13 Hz。此时刻地震波频率分布最宽，在10～40 Hz的范围内都有分布。最后高频成分迅速衰减，只剩余13 Hz分量持续了较长时间。

将该测点的水平径向分量（X轴）以及水平切向分量（Y轴）信号分别代入MP-WVD算法，得到其时频分布情况，分别如图13、14所示。

从图13、14中可以看出，水平切向振动信号的频率中心为21 Hz，水平径向振动信号在21 Hz和13 Hz处都有能量聚集。3个方向的振动信号均具有初始频带宽、高频衰减快的特点。不同点在于：水平切向的信号没有出现持续时间较长的13 Hz分量，且水平切向的能量分布明显比其他2个方向的更集中。

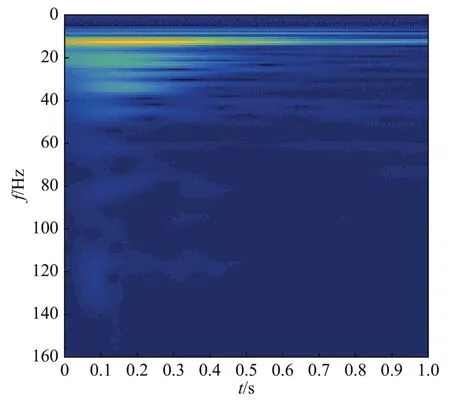
图12 小波变换结果Fig.12 Result of wavelet transform

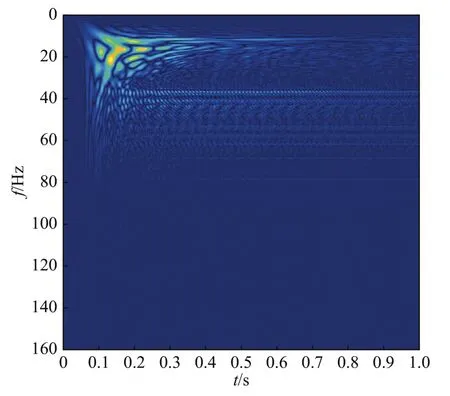
图13 水平径向分量（X轴）Fig.13 Horizontal radial component

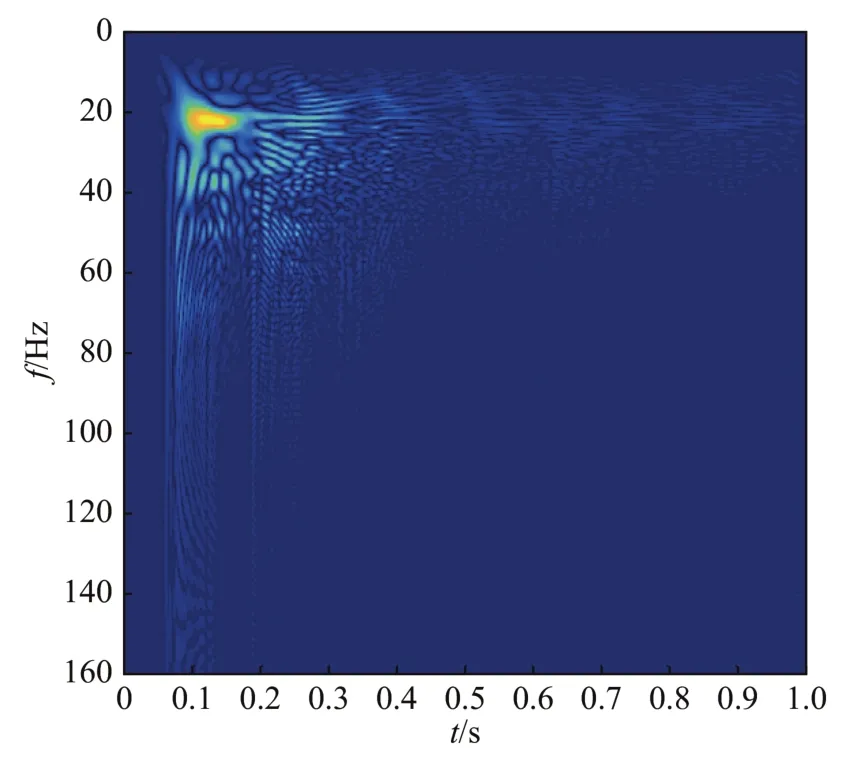
图14 水平切向分量（Y轴）Fig.14 Horizontal tangential component

对信号的时频分布函数分别进行时间积分和频率积分，得到信号的瞬时能量谱如图15所示，频率边际谱如图16所示。

图15 瞬时能量谱Fig.15 Instantaneous energy spectrum

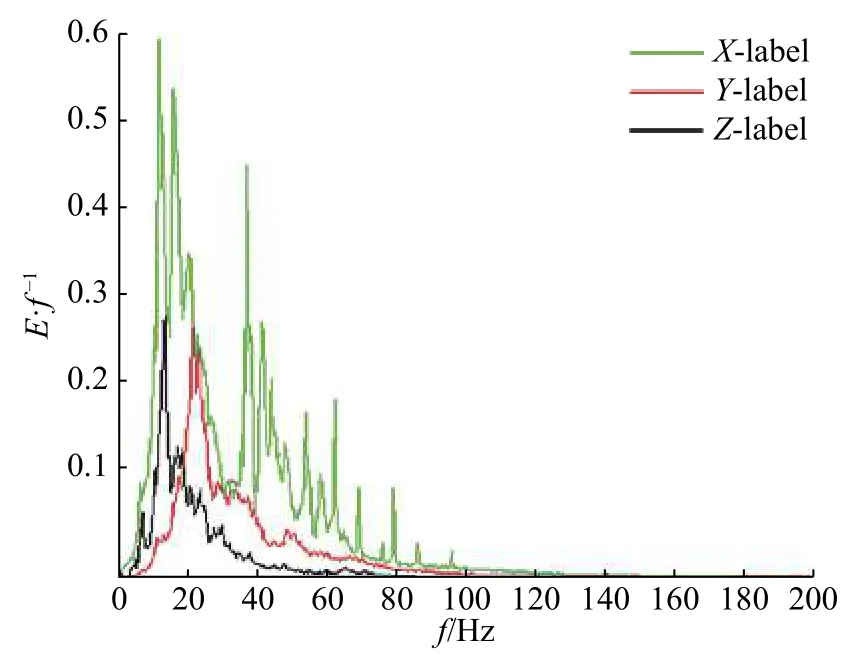
图16 频率边际谱Fig.16 Marginal spectrum

频率边际谱中纵轴E·f1表示能量在频率轴的分布密度, 量纲为J/Hz。

不同方向的传感器收集的地震波类型不同，其中瑞利波的质点运动方向对应X轴和Z轴，勒夫波的质点运动方向对应Y轴和X轴。边际谱纵坐标E·f-1表示能量在频率轴上的分布密度。由瞬时能量谱可以看出，水平切向（Y轴）的振动峰值率先到达，铅垂方向（Z轴）的振动峰值有较大的时延，而水平径向（X轴）的振动有多个峰值。4个方向的瞬时能量曲线反映出了在此次爆破引起的振动中，勒夫波率先到达测点，瑞利波相较勒夫波有约0.05 s的时延。

频率边际谱反映出信号的各个频率成分在时间全局上的累加，与傅氏幅频谱意义不同的是，傅氏谱只能反映信号的频率成分存在的概率而不能描述每个分量在整个振动过程中的能量份额。由图16可以看出，水平切向和铅垂方向振动频率较为集中，其频率中心分别为13 Hz和21 Hz。水平径向的振动由于混杂了勒夫波和瑞利波两个成分，所以具有多个频率中心。尤其需注意的是在36 Hz左右，X轴信号的边际谱有较强峰值出现，但在时频谱上并未见较强的时频能量集中，表明能量在此频率处集中但在时间上并不集中，边际谱的峰值是由于全局时间累积产生的，这种峰值小但加载时间长的特殊能量加载形式也需高度重视，防止产生损伤累积效应。

将南山村测点以及人家村测点所采集到的数据代入算法进行处理，得到的结果如图17、18所示。

图17 南山村测点数据分析结果Fig.17 Data analysis result of Nanshan village

图18 人家村测点数据分析结果Fig.18 Data analysis result of Renjia village

从图17、18中可以看出，由于测试点距离起爆点较远，瑞利波在传递过程中的色散效应产生了到达时间差，导致振动能量在时域上的分布更分散。

在频域上，能量分布更加向低频集中，绝大部分能量分布在10～20 Hz频带，20 Hz以上频带几乎没有分布。可以看出在爆破地震波中，高频成分衰减较快，而低频成分传播较远，爆破远区的抗震设计当以应对10～20 Hz频段的低频振动为主。

4 结 论

（1）将MP算法与WVD分布结合，有效地消除了交叉项的干扰，进而发挥出WVD分布对瞬态信号敏感以及高分辨率的特点。引入HHT算法对信号的瞬时频率以及瞬时相位先行确定，可有效降低计算复杂度，机时平均可缩短至之前的约2%。（2）改进型MP算法用于处理地震波数据有着很好的去燥效果，能在尽量保留信号局部特征的基础上剔除噪声信号，相比小波滤波以及EMD滤波性能较为突出。（3）MP-WVD算法对于核电爆破施工振动信号的分析结果较之小波变换方法具有更高的分辨率以及细节刻画能力。（4）由WVD时频谱衍生出的瞬时能量谱能够清晰地反映出信号的能量峰值到达时间以及加载次数。频率边际谱能够描述任意频率成分在时间全局上的累积，这些特性在研究结构动态响应过程中均可纳入参考。