空间站对日定向装置半物理试验台关键技术

刘明洋，贺 云,3，徐志刚,3，白鑫林

(1.中国科学院沈阳自动化研究所，沈阳 110016；2.中国科学院机器人与智能制造创新研究院，沈阳 110016；3.中国科学院大学，北京 100039)

0 引 言

我国航天技术快速稳固发展，运载火箭[1]、交会对接[2]、临近空间飞行技术[3]、空间在轨服务技术[4]、空间操控机械臂[5-6]、太空环境地面模拟[7]等方面取得巨大进步。在2020年前后，中国将建成和运营近地载人空间站，成为独立掌握近地空间长期载人飞行技术，长期开展近地空间有人参与科学技术试验，综合开发利用太空资源的国家[8]；同时结合我国科学发展需求，借鉴国外空间站空间科学应用开展情况，我国空间站将开展空间科学应用[9]。空间站电源由柔性太阳电池帆板提供，太阳电池帆板技术将朝着高效率、低成本、轻质量、长寿命、高可靠性的方向发展[10]，空间站通过驱动机构实现帆板对日定向控制，其中柔性太阳电池翼和驱动机构等关键技术需要进行验证[11]。建立对日定向装置半物理试验台的目的是实现对日定向装置承载性能、驱动控制性能测试，考核对日定向装置驱动柔性负载动态控制性能。大型太阳电池帆板具有大尺度、大质量、大惯量、刚柔混合等特点[12]，这些特点导致验证方式具有高难度，采用半物理仿真方式能够节约成本，且具有可行性。

对日定向装置半物理试验台原理如图1所示，利用动力学仿真单元实时解算柔性帆板对对日定向装置的反作用力矩，通过指令方式利用高精度加载单元实现对对日定向装置的加载。其中帆板模型动力学模型输入为对日定向装置驱动角加速度，根据圆光栅测量角位置计算角加速度。

图1 空间站对日定向装置半物理仿真试验台原理Fig.1 Principle of space station Sun-tracking unit semi-physical system

文献[13]利用Adams和Matlab仿真建立了扭振系统半物理模型和全物理模型，验证了半物理方案的可行性；文献[14]通过建立实物扭振系统验证了半物理试验台能够实现力矩加载的正确性；文献[15]通过设计控制器提高系统带宽提高了半物理试验台加载精度、带宽和响应速度。用商用软件对帆板模型进行动力学计算，无法进行实时计算与数据交换[16]，因此需要建立柔性帆板数值计算模型，利用动力学仿真计算机对加载力矩进行实时解算。文献[17-18]通过数学方法利用设计跟踪微分器间接估计输入信号的微分信号和二阶微分信号，有效避免差分放大噪声，能够利用二阶跟踪微分器求取加速度信号，有效抑制噪声信号。本文针对半物理试验台的高刚度机械支撑系统设计、运动误差高刚性无附加力适应、大型柔性帆板动力学模型建模、跟踪微分估计角加速度等关键技术进行阐述，并利用仿真试验和实物试验对半物理试验台和对日定向装置进行试验和考核。

1 机械系统设计

加载单元模拟力矩为非线性动态变化力矩，机械支撑系统的受迫振动会吸收加载系统能量，机械支撑系统刚度越高，吸收加载系统能力越少，加载模拟精度就越高；同样传动系统间隙会使加载力矩发生抖动而使加载力矩失准；为保证加载频率高加载精度准，同时避免加载单元与支撑连接系统共振，为避免激发其谐振，一般控制系统设计理论要求机械结构基频应大于控制系统带宽5倍[19]，因此要求机械支撑系统具有超高刚度。

1.1 支撑连接机构

机械系统支撑主体主要包括龙门柱体、底部支撑、水平滑台和纵向滑台；与对日定向装置连接的部分为扰动力矩传感器、连接机构法兰、气浮联轴节等。

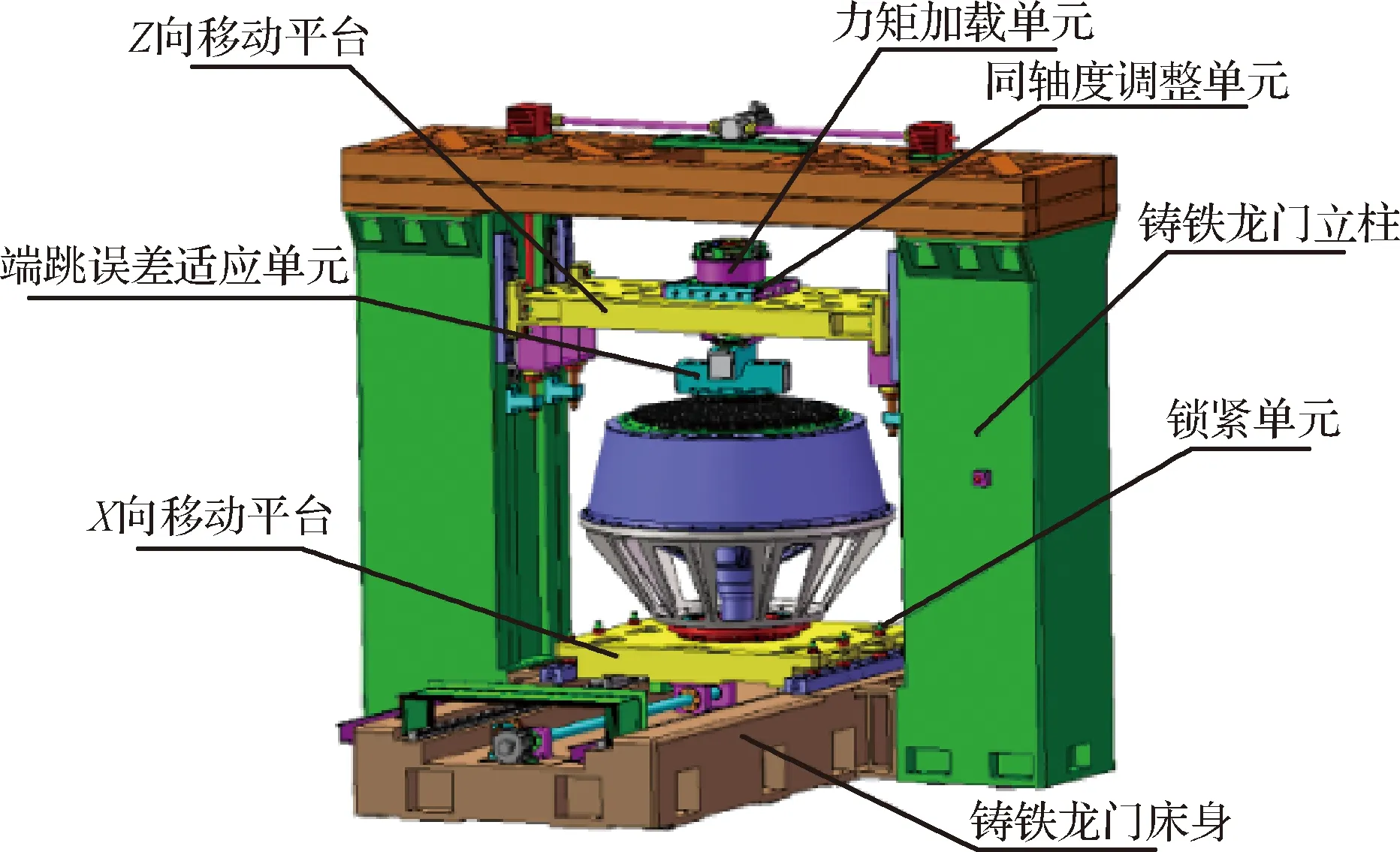
图2 机械系统设计及组成结构图Fig.2 Mechanical system design and structure

支撑连接单元设计时，在满足功能要求的基础上，通过加强各个连接部分提高其刚度，并利用Ansys软件对其进行分析，连接机构各部分一阶频率如下表所示。

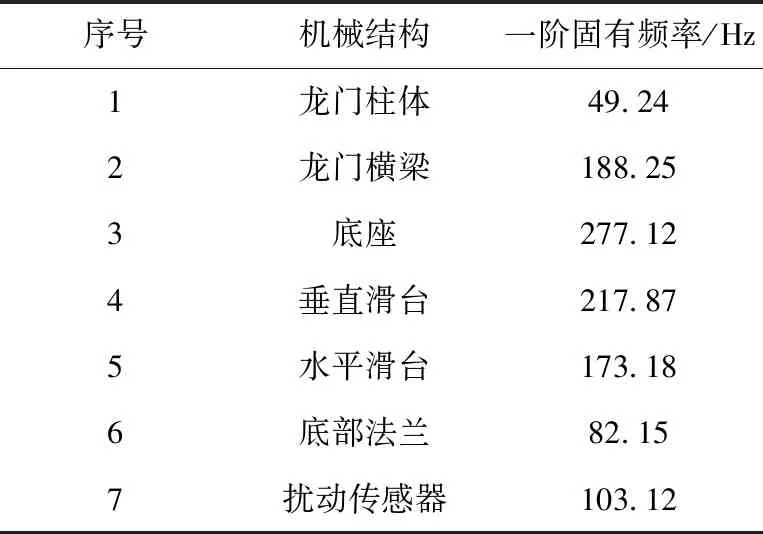
表1 连接机构各部分一阶固有频率Table 1 The first order natural frequency of each part of the connection mechanism

各部分结构有足够高的固有频率，因此保证系统整体有较高刚度，不安装被测机构对试验台一阶固有频率为44.63 Hz，安装产品后系统整体一阶固有频率为25.38 Hz，仿真分析结果如图3所示。

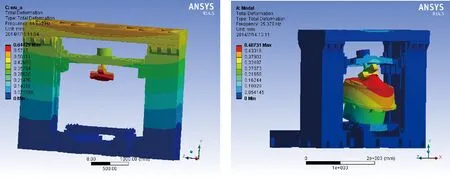
图3 试验台整体一阶振型图Fig.3 The first order natural frequency of the semi-physical system

1.2 加载单元

如图4所示，加载单元由加载电机、力矩传感器、圆光栅、气浮联轴节等组成。加载单元设计首先要保证角度测量精度，加载力矩测量精度；其次要消除对日定向装置端跳误差影响，减小作用于被测对象的额外重力；最后要保证加载传动的整体刚度，提高系统响应速度。

图4 气浮联轴节刚度测试图Fig.4 Test of the air floating coupling stiffness

对日定向装置在特殊工况试验时其输出端运动具有较大的端跳及径向跳动误差，为保证加载试验中不影响对日定向装置受力状态，需要在加载单元加载过程中无附加力柔性适应对日定向装置运动误差，同时保证整个系统的传动刚度，“一柔一刚”的矛盾要求对系统连接环节的设计与实施增加了难度。

加载单元与对日定向装置连接结构采用十字交叉气浮联轴节，它具有平面内两个方向气浮运动，气膜初始厚度为0.008 mm，气膜平均压强0.4 MPa时保证加载方向具有高刚度；气浮联轴节在垂向留有间隙垂向运动通过气浮导柱实现，可近似无阻力适应径向跳动误差。如图4所示，分别在O，A，B处放置角度测量装置，通过加载力矩和测量角度，拟合加载单元和气浮联轴节刚度，计算结果气浮联轴节刚度为10195.7 Nm/(°)、加载单元刚度为8984.7 Nm/(°)。加载单元和气浮联轴节的高刚度保证半物理试验台能够快速响应加载指令力矩。

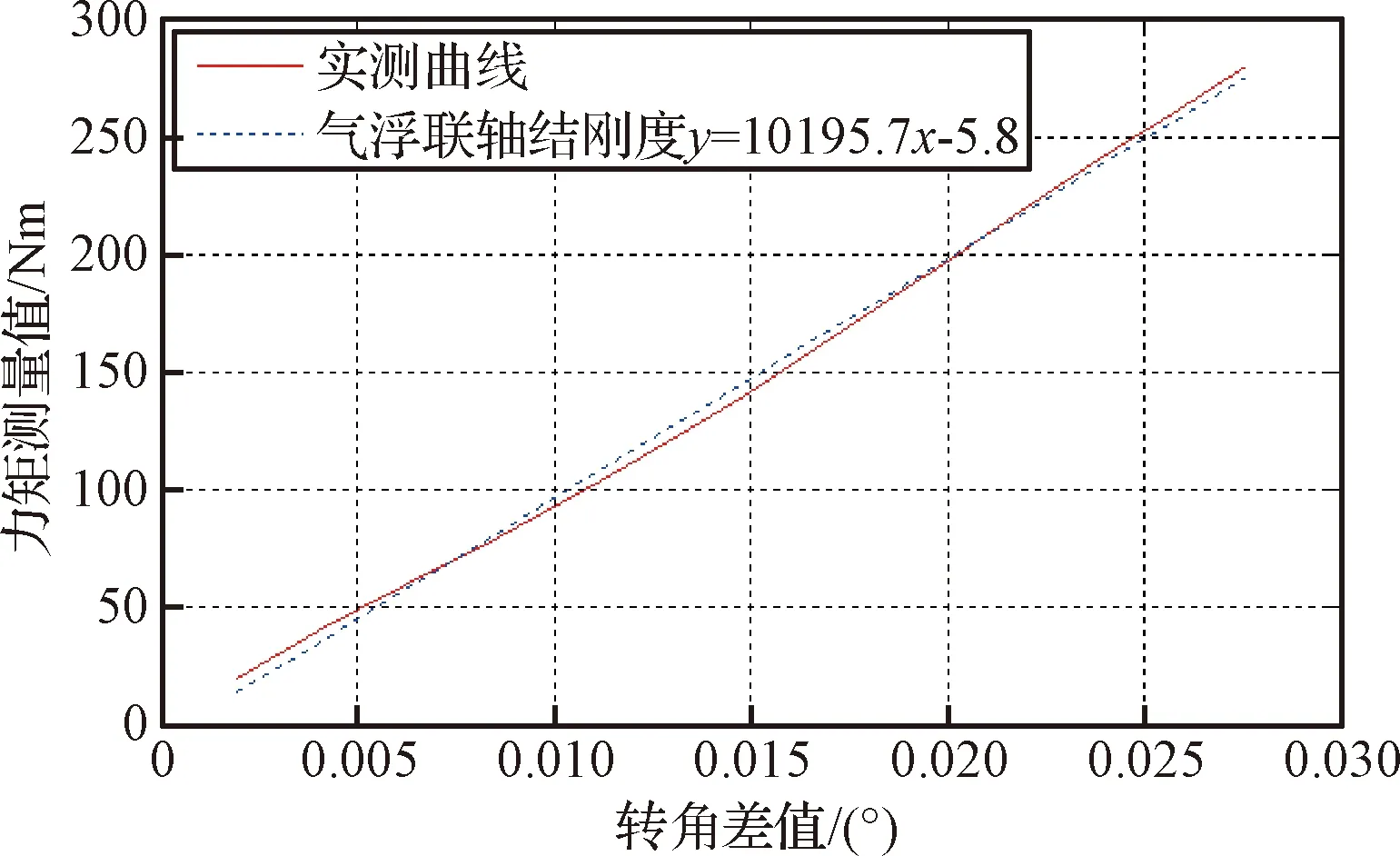
图5 气浮联轴节刚度测试结果Fig.5 Test stiffness results of the air floating connecting flange

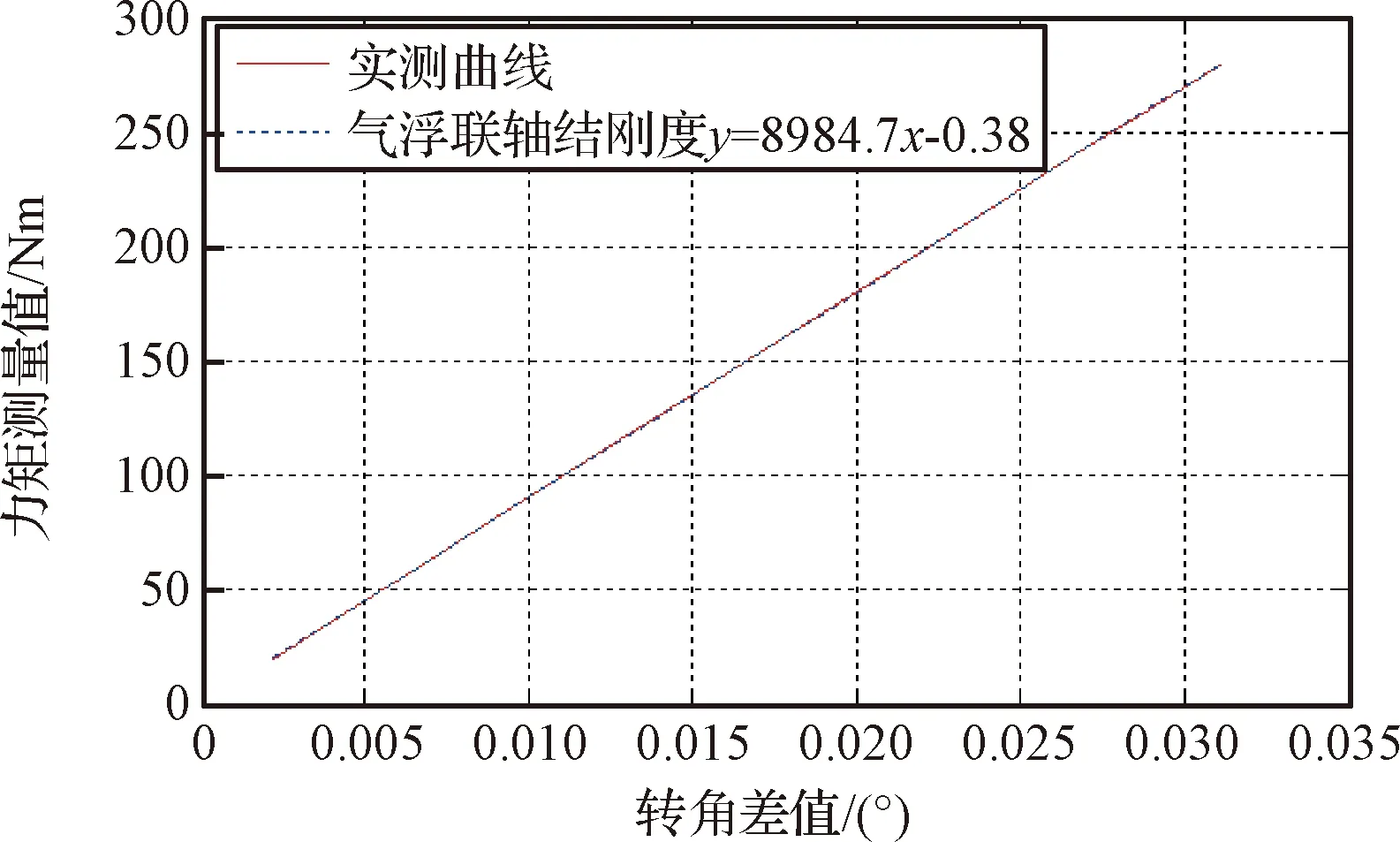
图6 加载单元刚度测试结果Fig.6 Test stiffness results of the loading unit

2 柔性帆板动力学建模

动力学模型计算的准确性是实现高精度半物理试验的基础，但是大尺度太阳能帆板有大惯量、大柔性、模态密集等特点，给对日定向装置柔性负载建模带来较大困难。针对中心刚体加柔性体结构附件进行动力学建模，采用混合坐标法和有限元方法对系统离散，并用Lagrange方程建立柔性动力学方程，最后利用威尔逊法进行离散化处理，利用动力学仿真单元进行实时解算。

2.1 坐标系定义

如图7所示，空间站由多套柔性帆板组成，以一套柔性帆板为例建立动力学模型，其中OiXiYiZi为惯性坐标系，原点Oi在空间站质心位置；ObXbYbZb为中心体的连体坐标系，原点Ob建立在中心体质心位置；OaXaYaZa为太阳电池阵的浮动坐标系，原点Oa建立在太阳电池阵未变形质心位置。

图7 空间站组合体几何坐标系定义Fig.7 Definition of the space station geometric coordinate system

2.2 拉格朗日函数

带柔性的系统动能T包括中心刚体和柔性体的动能，设具有N个柔性体，Tb和Tai分别表示中心刚体和柔性体i的动能，则系统动能为：

(1)

用模态坐标对柔性体i的结构变形进行模态展开，相对系统质心的静矩为零，则可得到系统的动能为：

(2)

式中:Ms为总质量，Is为相对本体坐标系的惯量矩阵，Ftai为柔性体振动对平动的柔性耦合系数矩阵，Fai为柔性体振动对柔性体转动的耦合系数矩阵，Fsai为柔性体振动对转动的耦合系数矩阵。

柔性建模中的势能V主要为柔性体的变形能。以Vi表示第i个柔性体的变形能，则有：

(3)

式中:Λai为柔性体i的刚度矩阵，建立系统的Lagrange函数为：

(4)

2.3 帆板动力学方程

带柔性附件的动力学方程：

(5)

将Lagrange方程及其准坐标形式(5)应用于式(2)～(4)，并根据基本假设忽略二阶小量，进行简化整理，就可获得柔性系统的动力学方程，带单套转动的柔性太阳电池阵动力学方程：

(6)

式中:Ps为作用在组合体上的作用力，Ms为作用在组合体上的作用力矩，Ma为作用在柔性体上的作用力矩，Ω为模态频率对角阵，且Ω2=Λ。基于传统混合坐标法原理建立了完整的太阳电池阵与驱动机构的刚柔耦合动力学方程。

2.4 Wilson θ法数值计算

考虑半物理试验台要求根据输入角加速度实时计算帆板作用在对日定向装置的力矩作为加载单元的指令输入，需要将挠性帆板模型进行数值计算。以线性加速度法为基础，引入参数θ>1，在时间域t～t+θΔt范围内，设加速度线性变化，且在任意时刻满足t+θΔt时刻运动方程：

(7)

则在时间段t～t+θΔt内任意时刻t+τ(0≤τ≤θΔt，并取τ=θΔt)的加速度、速度和位移：

(8)

由于已经假设在时间域t～t+θΔt范围内加速度为线性变化，因此外激励Qt也为线性变化，即

Qt+θΔt=Qt+θ(Qt+Δt-Qt)

(9)

代入可得：

(10)

并令τ=Δt，求得t+Δt时刻的位移、速度和加速度：

(11)

2.5 帆板动力学模型校核

为校核帆板数值模型正确性，利用商用软件Adams建模进行对比，正弦加速度激励输入力矩仿真输出曲线如图8所示。数值方法计算设定动力学仿真计算步长2 ms时，其仿真计算结果误差优于0.05%。

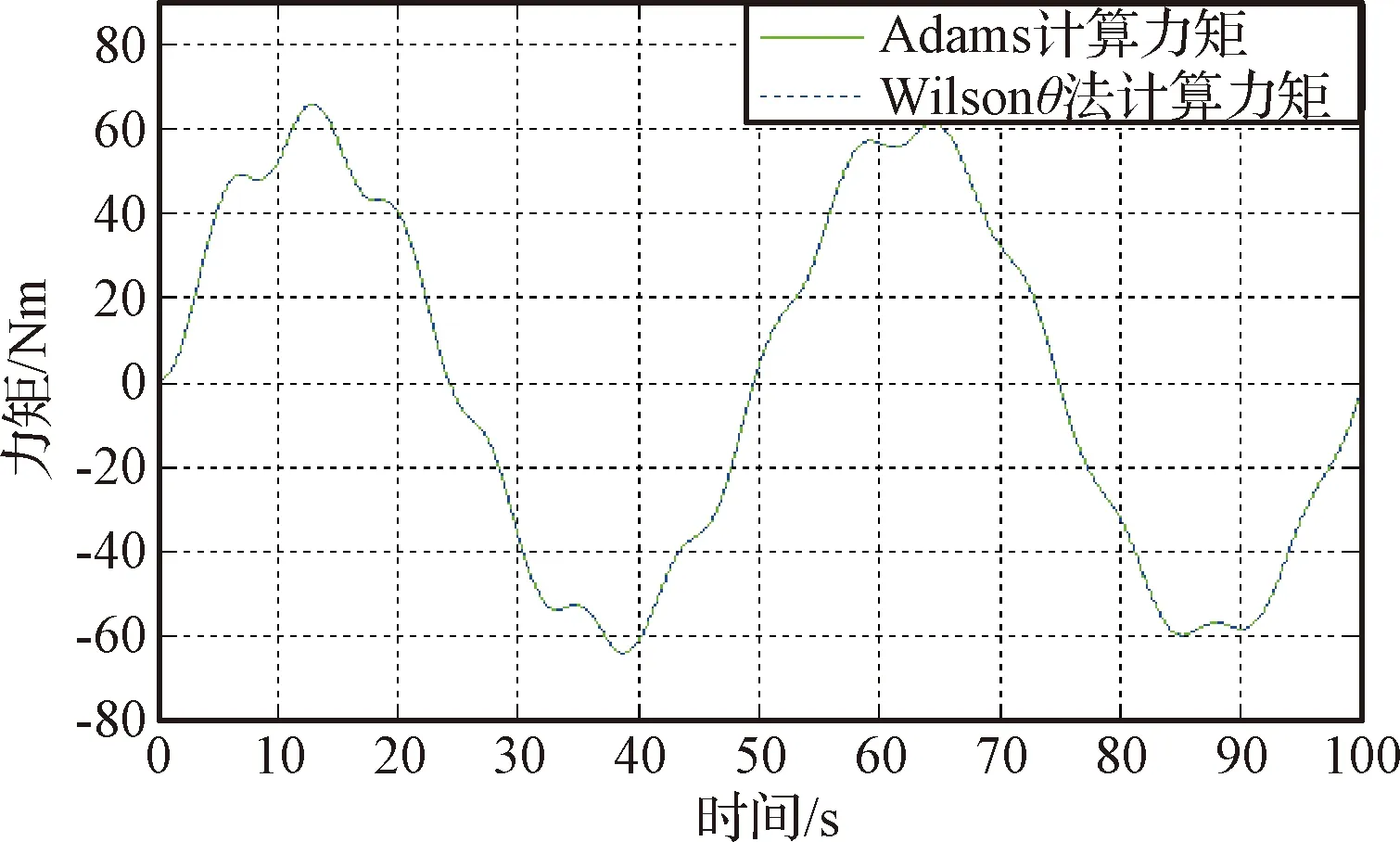
图8 Adams计算与数值计算输出力矩对比曲线Fig.8 The torque comparison curves of Adams calculation and numerical calculation

3 角加速度估计

半物理试验台的仿真模型输入为驱动机构的角加速度，输出为作用在对日定向装置的力矩，通过加载单元对驱动机构进行考核。试验台利用高精度光栅测量对日定向装置测量角度，常规角加速度估计，容易噪声过大导致帆板模型发散，最终导致整个试验无法进行。非线性跟踪微分器用于解决在不连续或带随机噪声的测量信号中，合理地提取连续信号及微分信号，它克服了经典差分算法的弊端，对噪声有较强的抑制能力。

3.1 跟踪微分法

非线性跟踪微分器：对它输入一个信号r(t)，它将给出两个输出变量x1(t)和x2(t)，其中x1(t)始终跟踪r(t)的变化，而x2(t)则是x1(t)的微分信号，当x1(t)快速跟踪r(t)的变化，x2(t)便可作为r(t)的近似微分。由于x1(t),x2(t)均可由r(t)的积分运算得到，避免了常规差分算法带来的噪声放大问题。在数值计算时，为了避免平衡点附近产生的振颤现象，实际使用时常采用基于欧拉方法离散化的微分跟踪器。

(12)

式中:T为采样时间；ε(k)为输入变量的估计误差；M为速度因子，主要影响跟踪速度；h为滤波因子，主要影响滤波效果。

(13)

(14)

(15)

利用两个跟踪微分器串联可得到二阶跟踪微分器，根据角度值可以计算角加速度。

3.2 角加速度估计结果

利用圆光栅测量低速转动时对日定向机构输出角度，利用二阶跟踪微分器和常规差分方法对角加速度进行估计，结果如图9所示。

图9 跟踪微分角速度估计Fig.9 The curve of the angle velocity estimation by tracking differential method

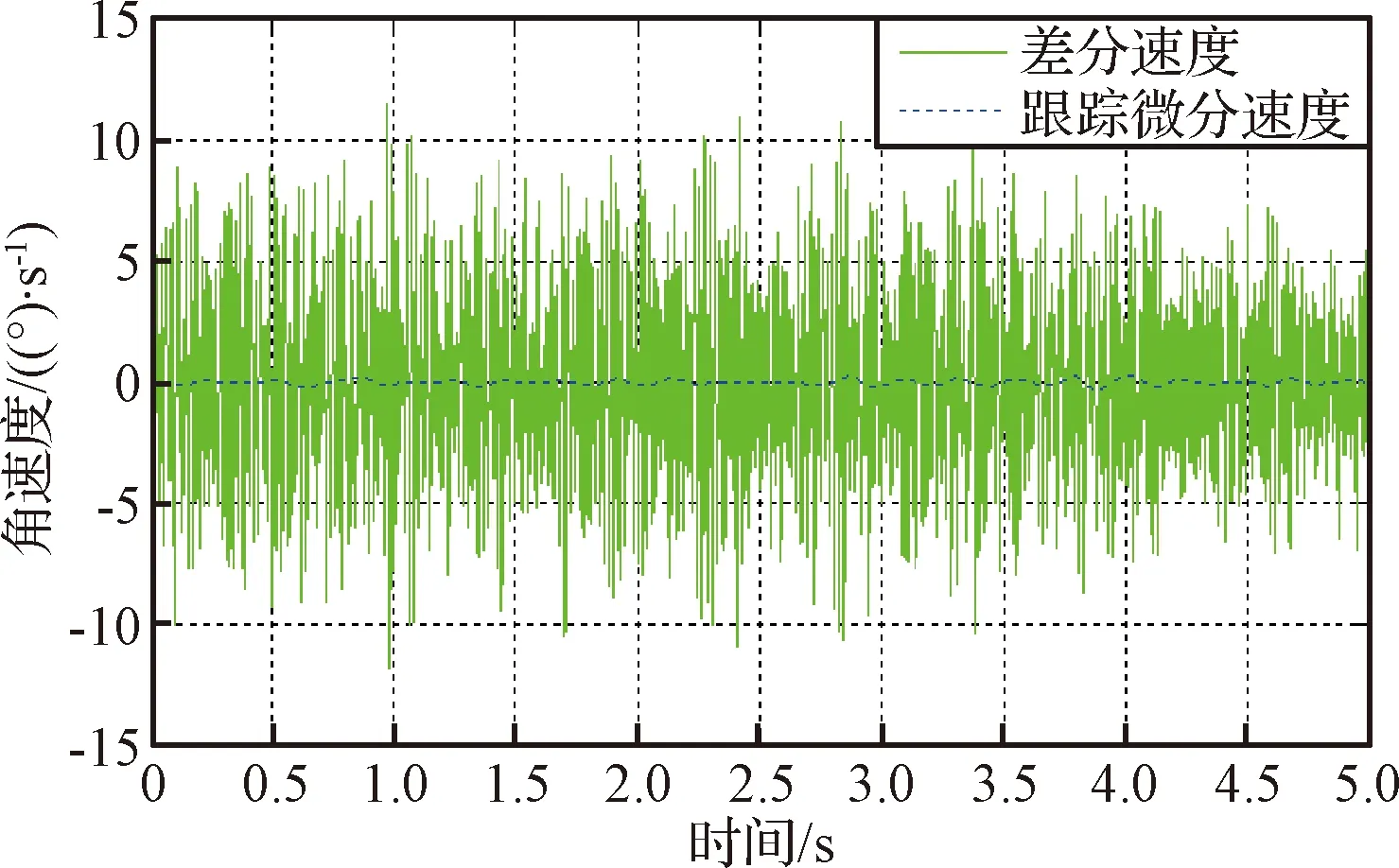
图10 跟踪微分角加速度估计Fig.10 The curve of the angle acceleration estimation by tracking differential method

从试验结果可以看出，跟踪微分有效抑制了角度测量噪声，大幅提高了角加速度估计的信噪比，能够更真实地估计对日定向装置的输出角加速度。

4 仿真与试验分析

加载单元响应速度、精度、系统带宽通过控制器设计得到保证，利用多正弦耦合曲线完成对加载单元进行校核试验；动力学仿真单元实时解算柔性帆板动力学模型，考核对日定向装置驱动柔负载动态控制性能，对整个试验系统加载有效性进行校验。

图11 半物理试验台实物图Fig.11 Physical structure of the semi-physical system

4.1 多正弦耦合试验

通过低频正弦与高频正弦叠加的方式，利用多个正弦信号耦合输出验证加载单元加载带宽与加载精度。如图12所示，半物理试验台稳定输出加载力矩，最大加载力矩偏差为0.42 Nm，稳态精度优于0.53%。

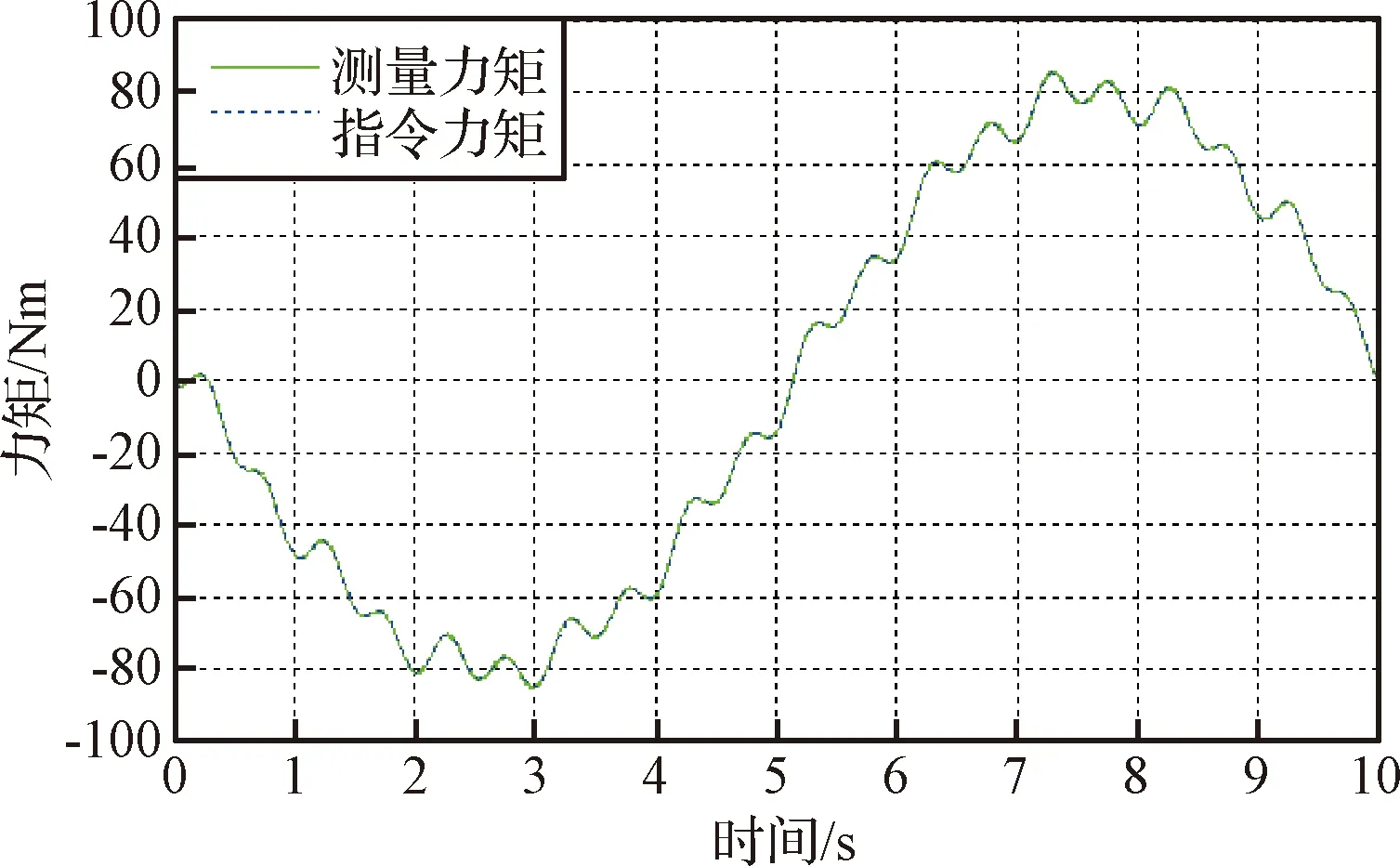
图12 多正弦耦合力矩加载曲线Fig.12 The load curves of the multisinusoidal coupled singals

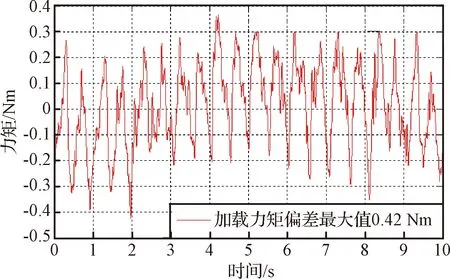
图13 多正弦耦合力矩加载偏差曲线Fig.13 The load curve of the multisinusoidal coupled singals deviation

4.2 帆板模型半物理仿真试验

驱动机构以0.06 (°)/s的速度启动运行，利用圆光栅测量角度，并利用跟踪微分估计角加速度，结果如图14所示。

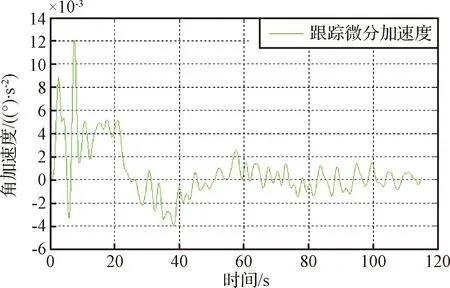
图14 角加速度估计Fig.14 The curve of the angle acceleration estimation by tracking differential method

估计角加速度作为柔性帆板动力学模型的输入，模型输出为加载单元的力矩指令。通过此工况对对日定向装置驱动柔性负载能力及半物理试验台若干关键技术进行验证，试验结果加载力矩曲线和加载力矩偏差如图15所示。

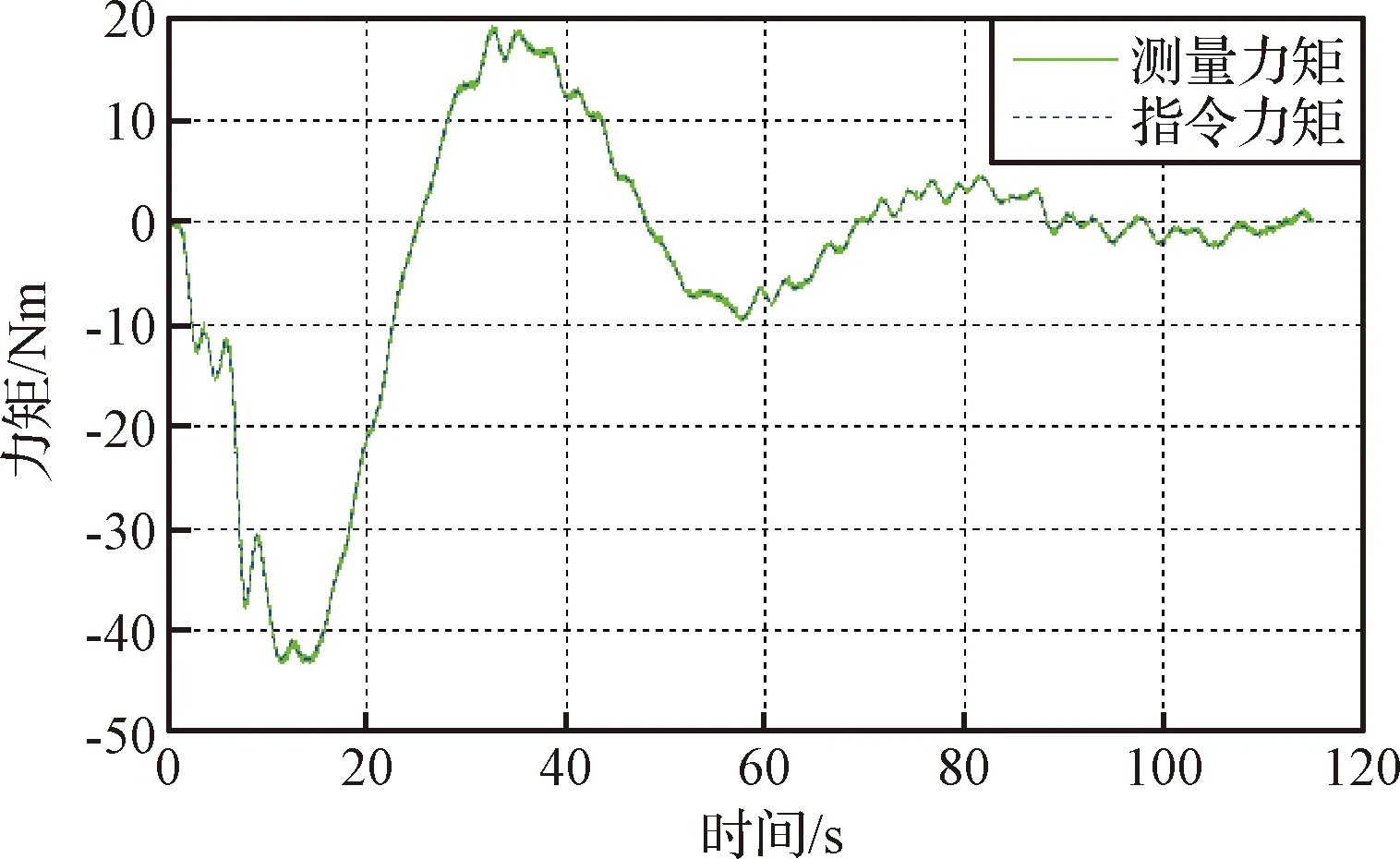
图15 帆板模型考核力矩曲线Fig.15 The load curves of the large flexible battery panel dynamics model

图16 帆板模型考核力矩偏差曲线Fig.16 The load deviation curves of the large flexible battery panel dynamics model

为测试对日定向装置的承载性能，驱动装置不仅能驱动柔性太阳帆板，空间站载荷环境中地球引力摄动、微重力、太阳光压、甚至可能遇到空间碎片等均可能对驱动引入干扰，为模拟这些干扰采用脉冲、斜坡、附加常值、高频振动等不同形式干扰作为附加输入信号实现对驱动装置的承载性能进行测试。如图17所示，在启动阶段对日定向装置施加若干单个脉冲干扰，特别地对日定向装置稳定运动时利用连续脉冲干扰进行扰动测试，试验结果表明存在干扰时对日定向装置仍能稳定工作。

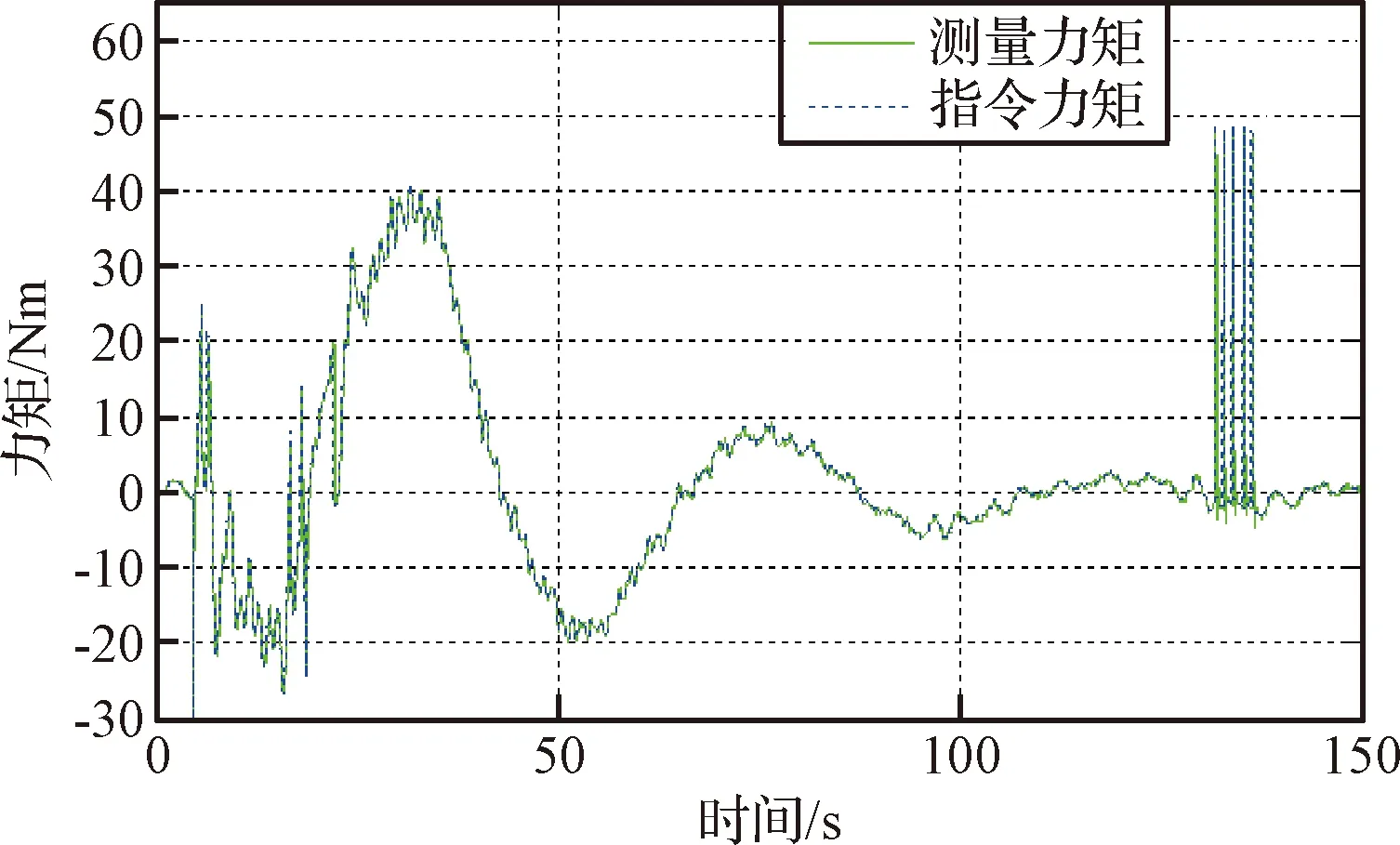
图17 帆板模型附加脉冲干扰力矩曲线Fig.17 The load curves of the large flexible battery panel dynamics model continuous pulse interference

5 结 论

通过设计和搭建半物理试验台实现对对日定向装置的地面考核。解决了高刚度传动、大型帆板动力学建模、角加速度估计等技术难题，最后利用多正弦耦合信号、帆板模型信号对试验台的响应精度、加载正确性进行考核，整个系统稳定运行，关键技术得到验证；综合多正弦信号与帆板信号考核结果，试验台加载力矩幅值0～85 Nm、频率0.01～3 Hz信号时，绝对精度优于0.85 Nm，相对精度优于1%。