数形结合在小学数学课堂教学中的运用

蒋丽美

（湄洲湾北岸经济开发区东埔中心小学，福建 莆田 351153）

数学教育是一种文化，数学教育与人的素养发展相结合，是数学学习的真正目的。数学具有高度的抽象性、系统性。如何与核心素养相联系，笔者认为，数形结合思想可以架起桥梁，化抽象为具体，化复杂为简约，真正助学生一臂之力，让学生借助数形结合自主探究、合作交流、深刻理解，逐渐提升数学素养。

一、运用数形结合进行计算教学，发展数学核心素养

运算能力是数学的“十大核心词”之一，是学生必备的数学素养。如何让学生拥有强大的计算能力？笔者认为要让学生掌握抽象的算法，应该先让学生经历算法的探究过程，在探究过程中明白算理。而要让抽象的算法易于理解，直观图是第一帮手。借助直观图数形结合，可以让数的抽象和图的直观对应起来，让学生真正理解算理，掌握计算方法，为形成一定的运算能力打好基础。例如：三年级学生学习《两位数乘两位数（不进位）》中，竖式计算从“两位数乘一位数”跨越到“两位数乘两位数”是学生认知上的一次大飞跃，探索算法是本课时的重点，理解算理自然而然是难点。“每套书有14本，王老师买了12套，一共买了多少本?”在探究14×12=（）环节，可以引导学生把每本书看成一个点，给学生提供14×12的点子图，让学生借助点子图把怎样算的想法表示出来。时间在一分一分中流逝，学生的思维火花在点子图中绽放。学生依托点子图，想法百花齐放。

图1

小小的点子图，充分展现了不同学生的思维轨迹，加上算式搭配，完美组合，学生不用解释，道理已在数形结合中。“仔细观察，这些方法有什么共同的特点？”学生通过交流发现，这些方法都体现了“先分后合”的解题思路，是把新知转化成已学过的旧知解决问题，是学生所积累的探究经验的流露，体现了解决问题方法的多样化。接着，教师可以让学生尝试用竖式计算。“你知道先算什么，再算什么吗？”教师把说理的机会抛给学生。“仔细观察，哪幅图能恰当地体现竖式的计算过程？”学生带着问题在观察、交流中发现竖式与图1-（4）有着密切的联系。他们惊奇地发现竖式其实就是先计算2套书有多少本，再计算10套书有多少本，最后合起来是12套书的总本数。直观的点子图有效地缓冲了学生在理解竖式算理中的难度，使竖式计算有图可依，有理可循，真正做到化抽象为形象。

图2

图3

“竖式计算中用到的4句口诀（二四得八、一二得二、一四得四、一一得一）计算的是哪一部分（图2）为什么第二层的积要错位写？能在点子图上找到竖式计算的过程并说明道理吗（图3）”

这样，借助点子图寻觅竖式计算的足迹，真正理解错位写的道理，突破教学难点，让学生真正明白竖式计算的道理，知其然而知其所以然。3次数形结合充分说明了数学知识是抽象的，但可以借助图形来说明道理，“以形助数更直观，数形结合明道理”。这样的课堂，学生不仅收获了知识，而且培养了几何直观意识，积累了以形助数的探究经验，发展了推理能力，数学核心素养的培养正在悄悄地进行。

二、运用数形结合进行概念教学，发展数学核心素养

数学概念是对现实世界的数量关系和空间形式的概括反映，它是用数学语言和符号揭示事物本质属性的思维形式，是对数学知识点的高度浓缩，它以文字的形式呈现，具有很强的抽象性。而小学生的思维以具体形象思维为主，对抽象的数学概念往往感到茫然，无法理解。因此，教师要善于运用数形结合，借助“形”来呈现概念中所描述的知识点，化解概念中纯文字的抽象，让学生在丰富的感性材料中建立清晰的表象，掌握概念的本质属性，从而建构清晰的数学概念。

例如，三年级学生在学习《认识几分之一》中，学生以前接触的事物都可以用整数表示，分数的认识是学生认识中的一次飞跃。当一个月饼要平均分给2个人的时候，该用什么数表示？学生的认知里遇到了障碍。很多学生会说出“一半”，至于“一半”该用什么数表示？他们就无从知道了。当教师介绍“把一个月饼平均分成2份，每份是这个月饼的二分之一，写作1/2”时，学生对1/2并不理解。这时就必须借助图形的帮忙了。教师可以设计两个活动帮助学生建立表象。

活动一：每组学生各准备一个圆形、一个长方形、一个正方形，让学生表示出图形的1/2（见图4）。当学生展示时，教师引导思考：图形不同，为什么它们都可以用1/2表示？学生借助图形发现不管什么图形，只要把它平均分成2份，其中的一份都可以用1/2表示。活动二：让每个学生用一张正方形纸表示1/4，由于学生的折法不同，涂色部分的形状也就不同。（见图5）

图4

教师再次引发思考：阴影部分的形状不同，为什么它们都可以表示成1/4？通过两个活动中图形的介入，学生对分数1/2、1/4有了感性的认识，他们清楚地认识到：只要把一个图形平均分，其中的一份都可以用分数表示。这样，有了图形的支撑，“以形补数”，有效地填补了学生学习分数时形象思维的空白，促进了学生对分数概念本质属性的理解，以形象促抽象，发展了观察、分析、实践能力，促进了几分之一模型的建构，有效地发展了数学核心素养。

图5

三、运用数形结合进行规律探寻，发展数学核心素养

数学是一门严谨、思维含量高的学科，探索规律在数学学习中占有很大的比例。由于小学生的思维以具体形象思维为主，对抽象的规律，往往无从入手，这时，如果能数形结合，定能一路高歌，顺利攻破。如：学生在探索连续奇数和的计算方法中，教师给学生出示“1+3+5+7+9+11+13+15+17+…+99=（ ）”，如果单纯凭借数据探索，学生探究起来有一定的难度。机智的学生想到“化繁为简”先探索“1+3+5+7+9=（ ）”，这是学生探究经验发挥的作用。教师给每组学生提供了必要的学具，“怎样摆出这些图形，可以很快计算算式的得数？”学生带着问题，借助图形先独立思考，并尝试摆一摆，方格图在学生的手中玩起了魔术。展示学生智慧的时间到了。如下图：

图6

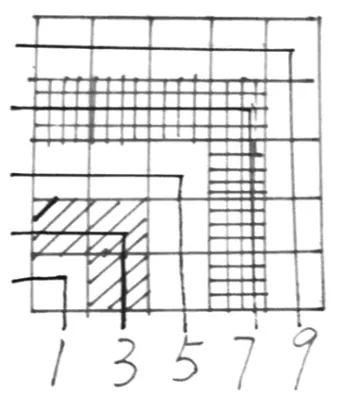
图7

很显然，摆成图7的学生引起了大家的关注。

“你这样摆的目的是什么？”在交流中发现原来学

生把它摆成正方形，1+3+5+7+9=（ ）转化成正方形的个数： 5×5=25。”至于“5”是哪来的？学生借助直观图不难看出，表示的是这组数的个数。显然，学生们初步学会用数学的眼光观察图形，借助图形用数学的思维分析问题，把连续奇数的和转化为正方形的总个数，这样的探究活动是否有价值？教师继续追问。1+3+5+7+9+11=（ ），照这样摆下去，可以摆成边长是几的正方形？1+3+5+7+9+11+13+15+17+…+99=（ ）呢？

就这样借助图形数形结合，学生经历操作、想象、交流、分析，初步发现“连续的奇数和，有几个就是几的平方”的结论。这时，教师抛出“3+5+7+9+11+13”，有5个数，就是5的平方等于25，对吗？”机智的学生再次结合图形说理，如果少了1，这些数就不能拼成正方形了，从而更加严谨地补充规律：“从1开始的连续奇数和，等于个数的平方”。这样，学生在学习中做到了“见数思形、以形助数”，真正认识到“数形结合百般好”。此过程拓展了学生的思维，发展了探究能力，质疑、归纳能力，同时模型思想也在落地生根，数学核心素养在悄然生长。

实践证明，数形结合在学生的数学学习中发挥着重要的作用，数在左，形在右，数形结合如影随形。数形结合搭建了学生从具体形象思维向抽象逻辑思维发展的桥梁，积累了活动经验，提升了学生的推理能力、探究经验，有效促进了数学核心素养的发展。