改进A星算法移动机器人路径规划

宋 宇， 王志明

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

路径规划问题在很多领域都具有广泛的应用，如机器人的自主无碰撞运行、无人机的避障突防飞行等。现有的路径规划方法包括蚁群算法、A星算法、D星算法、人工势场算法、模糊逻辑算法、神经网络算法、强化学习算法等。其中，A星算法作为一种经典路径规划算法，被广泛应用于路径规划问题中，但由于在栅格环境下A星算法只选择周围栅格的中心点加入open表中，导致路径点的选择局限于栅格中心点，路径转折角度固定为一些特定的离散值，从而产生了无效冗余转折或找到的最终路径不是最优。文献[1]提出了扩展Moore型邻居结构A星算法；文献[2]提出了结合跳点算法的A星算法；文献[3]采用了二叉堆优化查找open表中F值的方法，加快了A星算法的执行速度；文献[4]提出了去除冗余点的A星算法；文献[5]采用A星算法初始化信息素，用蚁群算法进行了机器人路径规划；文献[6]用蚁群算法对Hopfield神经网络的参数进行了优化；文献[7-8]采用了优化算法进行路径规划。

文中通过建立映射矩阵的方式提出了一种任意角度的A星算法，仿真实验表明，在栅格划分粗糙的情况下，改进算法效果显著。

1 相关算法

1.1 A星算法

A星算法是在Dijstar算法的基础上引入了启发函数，加快了算法收敛速度。A星算法的估价函数为

f(x,y)=g(x,y)+h(x,y)

(1)

其中,g(x,y)为起始点到当前考察点X(x,y)的实际距离值，h(x,y)为X(x,y)点到目标点的估计距离值，距离值函数h(x,y)一般取欧几里德距离(如式(2))或绝对值距离(如式(3))，gx、gy为目标点的x坐标与y坐标。

(2)

h(x,y)=|x-gx|+|y-gy|

(3)

A星算法不断将当前位置周围8个栅格的中心点加入open表，并不断取open列表中F值最小的点作为当前位置，直到当前位置的临近点出现目标点或open表为空为止，A星算法的流程如下：

1)初始化open表、opencost表、close表为空，将起点坐标加入open表，将起点的cost值0加入opencost表。

2)将open表中具有最小F值的点的坐标作为当前点，同时从open表与opencost表中删除这个点的信息，并把当前点的坐标加入close表。

3)依次计算当前点的邻居栅格中心的8个点的g值与f值，若这个点在close表中，则跳过这个点；若这个点既不在open表中，也不在close表中，则将这个点的坐标加入open表，同时将这个点的g值加入opencost表，并将这个点的箭头指向当前点。若这个点已经在open表中，则比较这个点之前的g值与通过当前点计算得到的g值的大小，若前者大，则修改这个点的g值为当前计算得到的g值，并将这个点的箭头方向指向当前点。

4)跳到2)，直到open表为空，或者open表中出现目标点为止。

1.2 粒子群算法

粒子群算法是一种模拟大自然群体寻优的优化算法，通过共享群体的适应度值大小来加速极值寻优过程。设D维粒子位置为xi=(xi1,xi2,…,xiD),粒子速度为vi=(vi1,vi2,…,viD)，种群中所有个体粒子目前为止适应度最优时的位置为p=(p1,p2,…,pD),到第k代为止种群中所有粒子的全局最优适应度值对应的粒子位置为pbk。则在每次迭代中粒子的速度更新公式为

(4)

位置更新公式为

(5)

通过不断迭代，最终算法保存了最优位置，即最优解。

2 改进A星算法

2.1 粒子群搜索

使用粒子群算法搜索当前栅格的邻居栅格内的最优粒子位置，如图1所示。

图1 搜索坐标边界

最中间的格子代表当前点所在的格子，首先在当前点所在格子的8个邻居格子内的线段上搜索到8个最优点，目标函数为F值(当前栅格的g值与当前栅格内的实际点到搜索栅格内搜索点的距离与搜索点到目标点的距离的和)，即搜索每个格子内直线上的F值最小的点，使用粒子群算法搜索时，粒子位置搜索范围限制在每个格子内的线段上。例如，粒子群算法在每个栅格内的给定范围搜索后得到的点如图2所示(黑色实心点)。

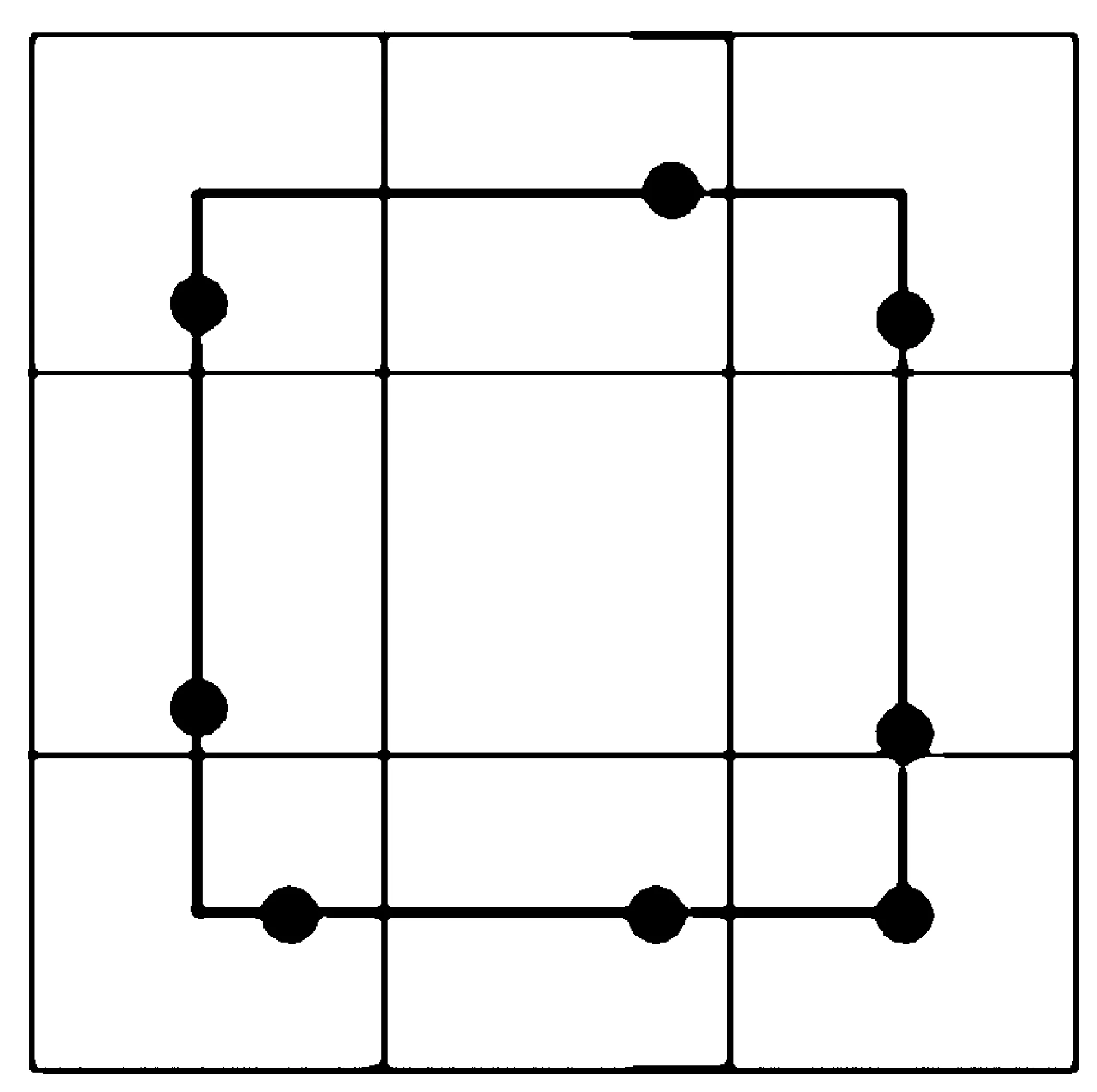
图2 搜索得到的点

将搜索到的8个最优位置存入M矩阵中。同时将搜索到的点的g值与f值存入cost与F数组中。

2.2 邻居格子属于open表

如果邻居栅格序号已经在open表中，目标函数为从当前栅格的M矩阵(目前所有栅格内的点的最优位置组成的矩阵)存储的当前栅格内的最优点到搜索栅格内点的距离与当前点的g值的和，上下左右栅格的搜索范围为栅格内黑色线段，如图3所示。

图3 搜索坐标边界

4个对角栅格的搜索范围为整个栅格之内(即若邻居栅格序号不在open表中，粒子群算法的搜索范围见图1，若栅格序号在open表中，粒子群算法的搜索范围见图3)。

比较被搜索栅格之前保存的g值与此次搜索到的点的目标函数值，若前者大，则将此邻居栅格的箭头指向当前栅格，并更新邻居栅格的g值与邻居栅格内M矩阵里存储的坐标值。

2.3 设置安全距离

为了避免规划出来的路径穿过障碍物，设置粒子的坐标距离最近障碍物中心坐标的阈值为d，若粒子(搜索过程中点的坐标)的坐标与所有障碍物中距离最近障碍物的中心点的坐标距离小于d，则将粒子群算法的适应度函数值额外增加100/distance，distance为机器人到障碍物中心的实际距离。若粒子的坐标距离最近的障碍物距离大于阈值d，则不增加。

2.4 改进算法流程

1)以起点为当前点，以2.1所述方法搜索起点的邻居栅格内的8个最优位置，以及这8个位置的g值(即从起点到这8个位置的距离)与f值。将起点序号加入close表，将8个邻居栅格的序号加入open表。将搜索到的8个栅格内对应的8个最优位置存入矩阵M中。将搜索得到的8个g值与f值存入cost数组与F数组中。

2)从F数组中选择f值最小的栅格为当前栅格，同时将此栅格序号从open表移入close表。

3)以当前栅格为中心，依次考察当前栅格的8个邻居栅格。若邻居栅格序号在close表中，则跳过此栅格；若邻居栅格在open表中，则以2.2所述方法更新邻居栅格的g值和f值，以及最优点位置；若邻居栅格既不在open表中，也不在close表中，则以2.1所述方法更新g、f值与最优位置,同时将该栅格序号加入open表。

4)若终点不在open表中，跳到2)，若终点在open表中，则算法结束。

3 仿 真

文中将粒子群算法迭代次数设置为10次，种群个数设置为10个。粒子群算法的速度最大、最小值不设限，粒子群搜索算法中的最大速度设置值为0.03，最小速度值为-0.03，阈值距离d设置为1.6。粒子群算法全局最优项前面的系数为2，局部最优项前面的系数为1.5。在Matlab2014a环境下进行了仿真。文中将平均转折角度定义为总的转折角度(每次转折时角度改变量的和)除以转折点的个数。由传统A星算法得到的路径和改进A星算法得到的路径分别如图4和图5所示。

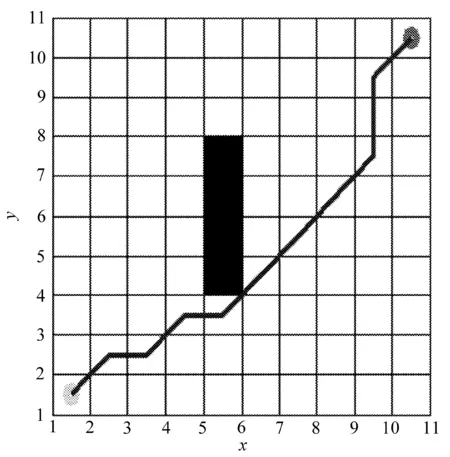
图4 A星算法路径

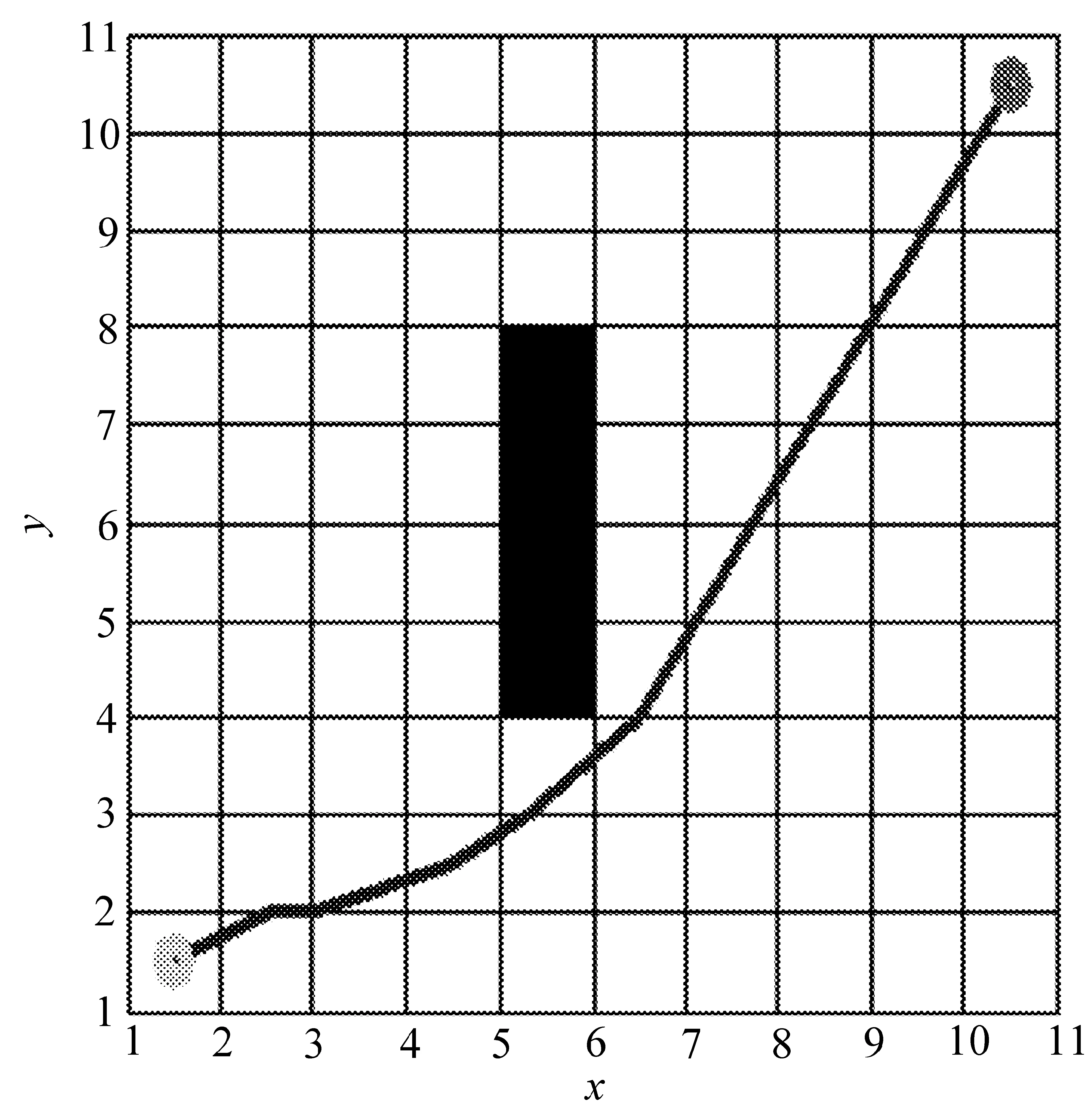
图5 改进算法路径

由图4和图5可知，改进算法找到的最优路径点较传统A星算法找到的路径点准确。

算法长度与转折角对比见表1。

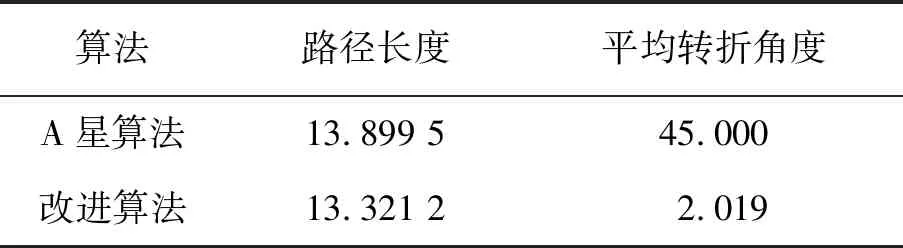
表1 算法长度与转折角对比

障碍物较多情况下传统A星算法规划得到的路径和障碍物较多情况下改进算法规划得到的路径分别如图6和图7所示。

图6 障碍物较多情况下A星算法路径

图7 障碍物较多情况下改进算法路径

障碍物较多情况下算法长度与转折角对比见表2。

表2 障碍物较多情况下算法长度与转折角对比

由表1和表2可以看出，由文中算法得出的路径长度较短且路径较平滑，更符合实际机器人的运动规律。另一方面，从图6和图7也可以看出，由于文中算法加入了对安全距离的考虑，得出的路径尽量远离障碍物，而不是紧贴障碍物的尖点，故文中算法得出的路径较安全。

4 结 语

通过设置栅格内搜索到的点与栅格中心点的对应关系以及搜索方式得到了栅格内的最优点，而不是直接选择中心点作为备选点，通过设置安全距离使得生成的路径不经过障碍物。仿真结果表明，改进算法得出的路径长度较短且路径较平滑。