卧式容器中液体体积的计算

丁 浩，刘 辉，刘勇营，陈先进

（浙江化工院科技有限公司，浙江 绍兴 312369）

卧式容器由于安装和使用方便等诸多因素，被广泛应用于化工、石油、冶金等行业中。在生产和贮运过程中，经常需要根据液位来计算出容器中的液体体积，以方便计量和操作。卧式圆筒容器内液体体积的计算是与其封头形式有关系的，因封头形式不同计算公式有所不同，封头形式主要有平封头、椭圆封头蝶形封头、球形封头等几种类型，但应用最广泛的主要为椭圆型封头卧式容器。本文以数学分析的方法详细推导出椭圆型封头卧式容器内液体体积的计算公式，以便准确地计算出容器的介质质量。

1 椭圆型封头卧式容器液体体积计算

椭圆型封头卧式容器[1]由直筒和椭圆型封头两部分组成，如图1所示。

图1 卧式容器结构示意图

图1 中卧式容器直筒部分的长度为L，半径为R，椭圆型封头曲面高度为b。

整个容器内物料的体积为直筒部分物料体积和两个椭圆型封头物料体积之和，即，式中V为卧式容器总体积，V1为直筒部分体积，V2为单个椭圆型封头体积。

1.1 直筒部分液体体积

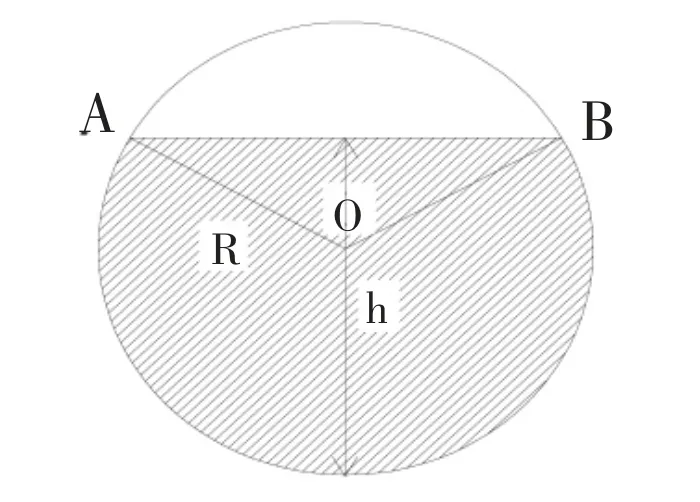
直筒内装有高度为h的液体体积等于液体淹没直筒横截面的弓形面积乘以直筒部分长度。直筒部分横截面结构（h＜R）如图2所示。

图2 直筒横截面结构示意图（h

横截面中弓形面积为：

则直筒部分液体体积

当液位高度h＞R时，横截面结构如图3所示。

图3 直筒横截面结构示意图（h＞R）

1.2 椭圆型封头部分液体体积

对椭圆型封头[2-3]建立如图4所示的空间直角坐标系。其中封头部分的长轴半径为R，短轴半径为b。

图4 直筒横截面结构示意图（h＞R）

在XOY面上的投影方程为x2+y2=R2，封头方程为

1.3 椭圆型封头卧式容器液体体积

1.3.1 液位高度h＜R时

1.3.2 液位高度h＞R时

2 常见几种液位体积计算公式

对于椭圆型封头卧式容器内液体体积[4-5]的计算，还可通过先计算K=h/D值，然后查表得出容积系数，用筒体及封头部分的总容积乘以容积系数得出，其中D=2R。下面介绍几个常用的快速计算公式。

（其中V为储槽总容积，单位m3）

3 实验验证及误差分析

现结合中试试验装置平台，通过向椭圆型封头卧式液碱储槽中补加液碱（30%氢氧化钠溶液，密度为1330 kg/m3）的方式对本文推导出的液体体积计算公式及常见的计算公式进行验证，并进行误差对比分析。液碱储槽结构示意图如图5所示。

由于液位计下端口至储槽底部有100 mm的液位显示盲区，故实验中液碱液位始终高于100 mm。液碱储槽配备称重远传及液位远传模块，实验开展前已完成校正和调试工作。

图5 液碱储槽结构示意图

打开液碱储槽进料阀门，并保持阀门开度不变，向储槽中匀速进料。当储槽内液位高度达到1.35 m时，立即关闭进料阀门，停止补加。为减少实验误差，进行多次实验并取平均值。液位及重量数据在每次实验结束后，从DCS后台系统中调取实验数据。实验数据及误差分析对比情况详见表6。

表6 实验数据及误差分析对比

图7 误差对比图

从图7中可以明显看出相对误差Er②和Er③数值均随着液位高度h的增大而逐渐减小，说明在低液位时，两个经验公式V①和V②的计算结果相对误差较大，与实际工况偏离严重。但是随着液位高度的逐渐增大，其相对误差逐渐减小。当液位高度达到80%后，Er②和Er③平均值分别为28.56%和4.57%。

图7中相对误差Er和Er①较小且数值随着液位高度h的逐渐增大而保持平稳，说明本文中推导出的体积计算公式V和经验公式V①在全液位高度范围内与实际工况更加吻合。但从表6中可以计算出，Er的平均值为0.16%，Er①的平均值为-0.87%，所以本文中推导出的体积计算公式V在实际工况下计算相对误差更小。

4 结语

本文以数学分析的方法推导出卧式容器内不同液位高度下对应的液体体积计算公式，并通过实验对其进行验证和误差分析，实验结果表明在全液位量程范围内相对误差仅为0.16%，与实际工况更为接近，同时可根据比重确定容器内的工况质量。此次公式推导为中试试验及生产装置提供了更加准确的计算方式，具有良好的实践意义。