并联驱动双向偏转平台设计与动力学分析

陈 纯 徐永帅 王佳伟 房 舟 魏碧辉

(陕西理工大学机械工程学院， 汉中 723001)

0 引言

与传统的串联机构相比，并联机构具有精度高、响应快、易于控制等优点，引起了国内外专家、学者的极大兴趣[1-2]。而结构简单、作业空间大、动力学求解简单、运动耦合度小、对机械零部件加工制造精度要求不高，以及对机构运动控制精度要求较低的少自由度并联机构更受到青睐[3-7]，许多学者对不同类型的并联机构进行了动力学分析[8-19]。目前学者们提出的并联机构多以Stewart、Tricept为原形的杆结构类型为主，本文提出一种并联驱动双向偏转平台，运用Lagrange法建立平台动力学模型并进行仿真分析。

1 并联驱动双向偏转平台机构

1.1 机构描述

并联驱动双向偏转平台如图1所示，平台主要由底座、滑块、电机、驱动拱、圆弧导轨、销轴、动平台、主动齿轮以及支撑板等构件组成，圆形动平台由在空间呈正十字交错且同心的两个半圆形外齿轮环(半径大小不同，称之为驱动拱)支撑，其中大驱动拱通过销轴8由转动副与动平台连接，小驱动拱通过销轴11由一种特殊的运动副(称为滑伸副)与动平台相连；大小驱动拱分别与半径不同的圆弧导轨(称为大、小圆弧导轨)相固联并由圆弧导轨副(分别由大圆弧导轨与滑块2、14，小圆弧导轨与滑块6、13组成)导向，滑块固联于置于底座1上的呈正十字布置的支撑板上，大、小驱动拱的偏转分别由主动齿轮16、15驱动，主动齿轮16、15分别安装在电机17、3的主轴上，电机17、3固定于底座上，从而实现动平台绕X、Y轴两个方向上的大角度偏转。

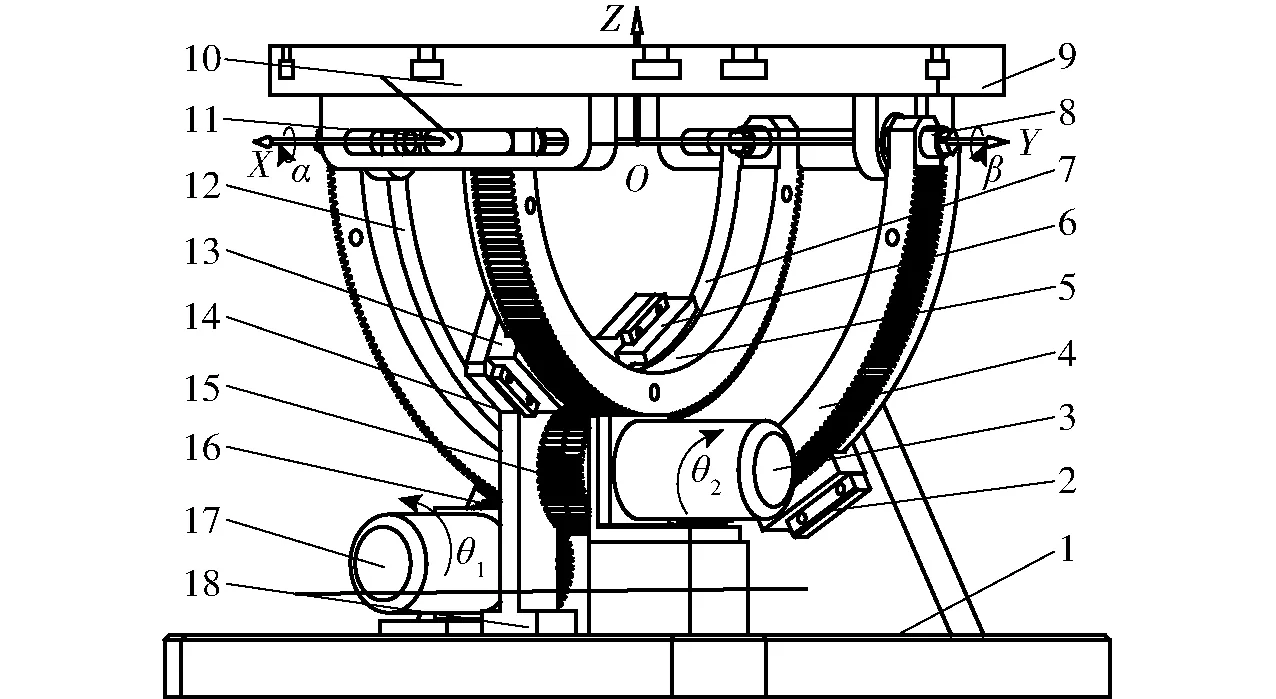
图1 并联驱动双向偏转平台模型Fig.1 Parallel bidirectional deflection platform model1.底座 2、6、13、14.滑块 3、17.电机 4.大驱动拱 5.小驱动拱 7.小圆弧导轨 8、11.销轴 9.动平台 10.滑伸副 12.大圆弧导轨 15、16.主动齿轮 18.支撑板

在该平台中存在一种特殊的运动副(滑伸副10)，如图2所示，该运动副在动平台同时作绕X轴和Y轴运动的过程中，与小驱动拱连接的销轴11会在与平台固联的U型孔中滑移并伸缩。

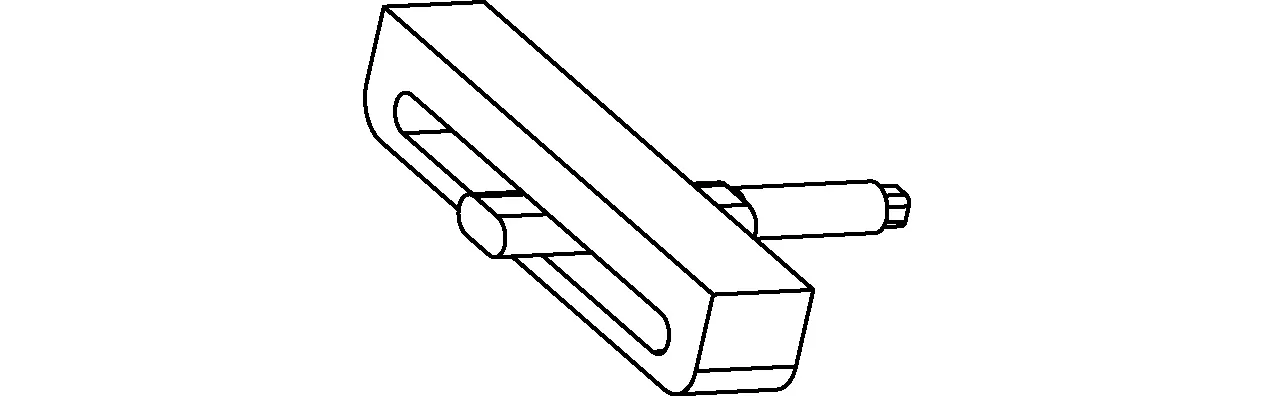
图2 滑伸副Fig.2 Sliding telescopic pair

1.2 自由度分析

在此平台中，由于大驱动拱的中心与销轴11的轴线共线、小驱动拱的中心与销轴8的轴线共线，且平台分别相对于XOZ、YOZ面对称，可看作该平台是沿对称面切分为含有4条支链的并联机构。由于4条支链中对称面两边的两条支链结构完全相同，故该并联机构可认为是2-GRR(FR)/GRR运动链形式的并联机构，其中G为齿轮副、F为平面副、R为转动副，滑伸副(FR)可看作是由平面副F和转动副R组合而成。采用修正的Kutzbach-Grnbler公式[20]计算其自由度

(1)

式中K——机构的自由度

n——包括机架的构件数目

g——运动副的数目

fi——第i个运动副的自由度

v——多环并联机构在去除公共约束因素后的冗余约束数目

ξ——机构中存在的局部自由度

为了增加并联机构的刚性和导向精度，此并联机构中大、小圆弧导轨副中分别含有两个滑块，因此该机构中含有两个冗余约束，即v=2；该机构中不含局部自由度，即ξ=0，其余未知量均较易得出，此处不再详细分析。

2 运动学逆解

如图1所示，假定动平台绕X轴与Y轴偏转角分别为α和β；主动齿轮15、16转动角分别为θ1和θ2；主动齿轮15与小驱动拱的齿数分别为z1和z2，模数为m1；主动齿轮16与大驱动拱的齿数分别为z3和z4，模数为m2。

动平台在绕X轴方向上位置解为

(2)

动平台绕Y轴偏转可简化为图3所示的几何关系，假设当动平台绕X、Y轴偏转角为α、β，由于滑伸副的存在使得小驱动拱转角并不等于β，而是β1，其空间关系如图3所示。

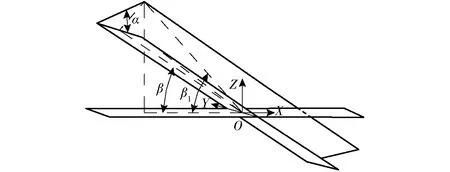
图3 动平台绕Y轴偏转示意图Fig.3 Schematic of deflection of moving platform around Y axis

由图3空间几何关系可得

(3)

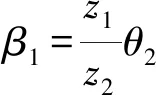
(4)

将式(2)、(4)写成矩阵的形式

(5)

对式(5)求其对时间的一阶导数即可得平台速度逆解，即

(6)

则并联驱动双向偏转平台的速度Jacobian矩阵为

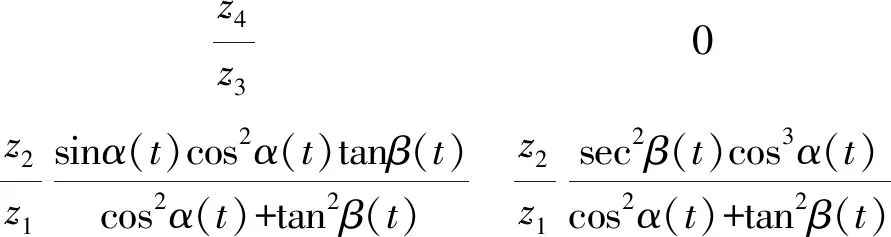
(7)

从平台的运动学方程可以得出，平台在绕X轴方向的偏转运动不受其绕Y轴方向偏转运动的影响；平台在绕Y轴方向的偏转运动受其绕X轴方向偏转运动的影响，存在耦合关系。

3 平台动力学建模

平台总动能T可表示为

T=∑Ti(i=4,5,7,8,9,11,12,15,16)

(8)

式中i——构件编号(图1)

其中构件4、5、7、12的动能可表示为

(9)

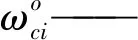
构件8的动能可表示为

(10)

构件11的动能可表示为

(11)

式中I11——构件11在自传回转轴下转动惯量

ωc11——构件11在自传回转轴下角速度

构件9的动能可表示为

(12)

构件15、16的动能可表示为

(13)

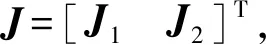
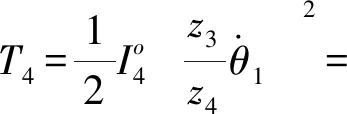
则可得平台总动能T为

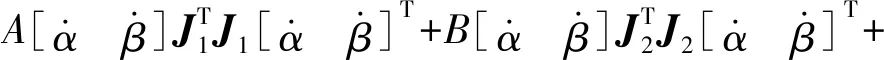
(14)

其中

根据虚功原理可得

QkΔqk=∑δW′=MΔφ+MkΔqk(k=1,2)

(15)

其中

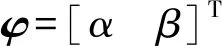
式中M——动平台所受的外力矩

Δφ——动平台的偏转角

Mk——电机输出的驱动力矩

qk——输入广义坐标

Qk——广义坐标下的广义力

对式(15)两边同时除以Δqk得

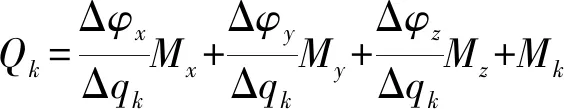
(16)

整理式(16)可得

(17)

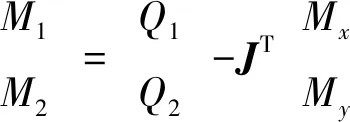
(18)

Lagrange方程为

(19)

将式(14)代入式(18)得

(20)

(21)

(22)

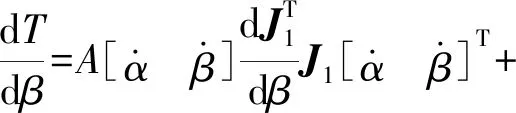
(23)

将式(20)～(23)代入式(19)得

(24)

(25)

将式(24)、(25)代入式(18)得平台的动力学模型为

(26)

4 动力学计算与仿真

依据所建立的并联驱动双向偏转平台的动力学模型，给出平台的参数以及施加在其上的外载，即可计算、仿真电机输出的驱动力矩。

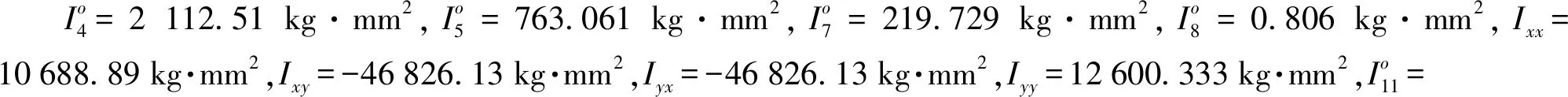
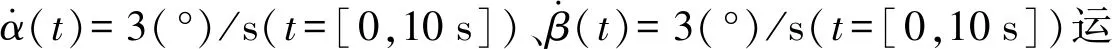
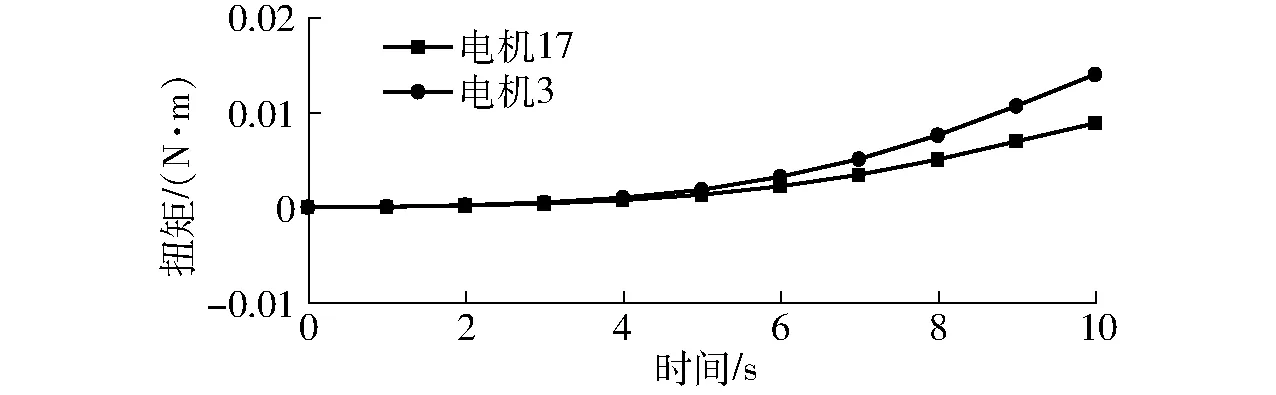
图4 空载时M1、M2曲线Fig.4 Curves of M1 and M2 under no load

由图4可知，驱动电机17输出力矩M1最大为0.009 1 N·m、最小为0.000 6 N·m；驱动电机3输出力矩M2最大为0.014 2 N·m、最小为0.001 1 N·m。

(2)动平台9受外力矩Mx=4 N·m、My=0，得出驱动电机3、17输出的驱动力矩M2、M1变化曲线，如图5所示。

图5中驱动电机17输出力矩M1最大为25.443 2 N·m、最小为25.431 2 N·m；驱动电机3输出的力矩M2最大为3.426 9 N·m、最小为0.006 7 N·m。

(3)动平台9受外力矩Mx=0、My=4 N·m，得出驱动电机3、17输出的驱动力矩M2、M1变化曲线，如图6所示。

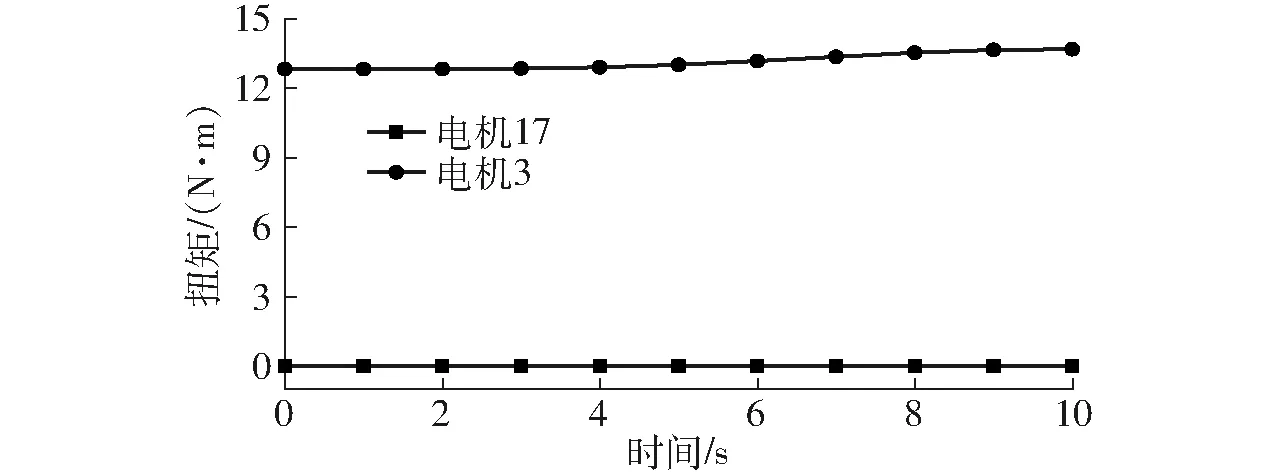
图6 绕Y轴带载时M1、M2曲线Fig.6 Curves of M1 and M2 when loading around Y axis

由图6可知，驱动电机17输出力矩M1最大为0.009 1 N·m、最小为0.000 6 N·m；驱动电机3输出力矩M2最大为13.658 2 N·m、最小为12.802 3 N·m。

(4)动平台9受外力矩Mx=My=4 N·m，得出驱动电机3、17输出的驱动力矩M2、M1变化曲线，如图7所示。

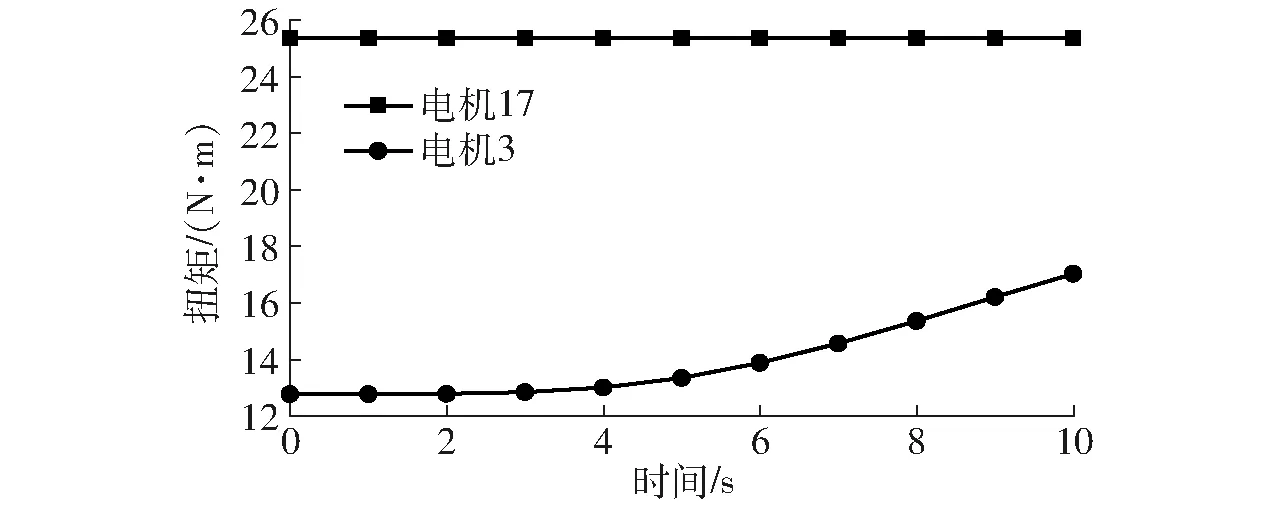
图7 绕X、Y轴均带载时M1、M2曲线Fig.7 Curves of M1 and M2 when loading around X and Y axes

图7中驱动电机17输出力矩M1最大为25.443 2 N·m、最小为25.441 2 N·m；驱动电机3输出力矩M2最大为17.071 1 N·m、最小为12.803 4 N·m。

从图4可以看出，当动平台上负载为0时，驱动电机17、3的输出力矩虽小但呈递增的趋势，说明随着动平台偏转角增加其重力产生的力矩也越大，电机17、3的输出力矩主要用来克服动平台及其相关组件重力产生的力矩。

当动平台上负载为0时，驱动电机17、3的输出力矩M1、M2虽呈递增趋势，但均很小(几乎为0)；由图7可知，当动平台在绕X、Y轴方向上同时施加大小相同的负载时，驱动电机17、3均输出较大的力矩，且M1>M2，故可知平台自身重力对驱动电机17、3的输出力矩影响很小，驱动电机输出的力矩主要用来克服外载。

对比图5、6可知，当动平台在绕X轴方向上施加负载、绕Y轴方向上为空载时输入力矩M1、M2均产生较大的变化；反之当动平台在绕X轴方向上为空载而绕Y轴方向上施加负载时输入力矩M2产生较大的变化，M1变化很小，故可知平台在绕X轴方向上的偏转不受其绕Y轴负载的影响，而在绕Y轴方向上的偏转存在耦合关系(受平台绕X轴负载的影响)，与平台运动学的结论一致，验证了平台动力学结论的正确性。

为了验证所设计平台的可行性与所建动力学模型的正确性，分别取t=1、3、5、7、9 s时各外载状态下理论计算值与仿真值进行比较，结果如表1、2所示。

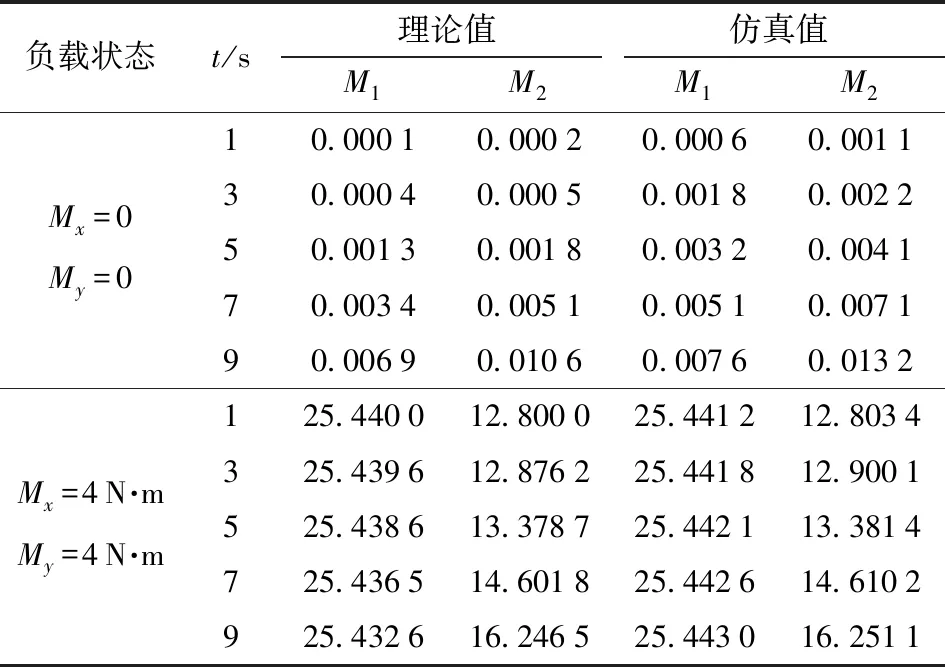
表1 绕X、Y轴空载与均带载时电机输出力矩Tab.1 Output torque of motor around X and Y axes under no load and even load N·m

由表1、2可以看出，动平台9在各种负载状态下驱动电机17、3输出力矩M1、M2的理论值与仿真值偏差很小(Δmax=0.010 4 N·m)，几乎相等，验证了模型的正确性。

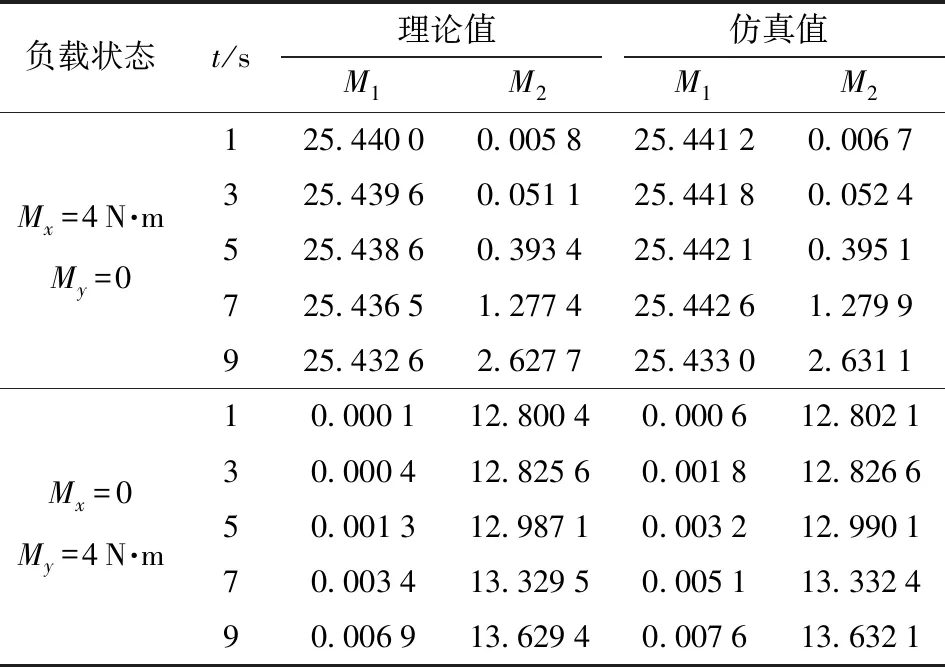
表2 绕X、Y轴分别单独带载时电机输出力矩Tab.2 Motor output torque when X and Y axes were loaded separately N·m

5 结论

(1)所设计的并联驱动双向偏转平台原理可行，动力学模型正确。

(2)从运动学和动力学分析可知，平台绕X轴方向上的偏转不受其绕Y轴方向上偏转的影响，而绕Y轴方向上的偏转受其绕X轴方向上偏转的影响，两者存在耦合关系。

(3)驱动电机输出的力矩除了克服由于平台偏转零部件重力所产生的转矩外，主要用来克服外载，这与实际工况相符。