4-PRR冗余并联机构驱动力与能耗优化

胡小亮 谢志江 吴小勇 刘 飞 卢 超 唐小斌

(1.重庆大学机械传动国家重点实验室， 重庆 400044; 2.重庆理工大学机械工程学院， 重庆 400054)

0 引言

在某大型连续式跨声速风洞半柔壁喷管段中，需要设计一种重载3自由度调整机构，调整其中的喉块段，从而实现对刚柔耦合变形协调、精度控制[1-3]。冗余驱动并联机构可以提高机构的承载能力与控制精度，获得较好的刚度特性及动态性能[4-5]。但冗余驱动中驱动数大于自由度数，驱动力与功率分配理论上有无穷多解，需要根据优化目标对其进行优化。

并联机构的动力学分析可以通过拉格朗日法、牛顿-欧拉法、凯恩法、虚功原理等方法[6-12]得到机构的动力学模型。DONG等[13]采用加权伪逆法优化了驱动力分配，并减小了最大驱动力。NOKLEBY等[14]采用无约束方法对冗余并联机器人的力旋量能力进行求解，结果表明冗余驱动能够明显提升机构的承载能力。王立平等[15-16]采用最小化驱动力的二范数对驱动力进行了优化。卿建喜等[17]提出了最小化驱动器最大瞬时驱动功率和最大瞬时驱动力的优化方法，与非冗余驱动方式相比，冗余驱动能够显著降低驱动器的瞬时负载和瞬时输出功率。LEE等[18-20]利用驱动力二范数及能量矩对2自由度冗余驱动并联机构进行了能耗优化，结果表明其明显降低了系统的功耗；文献[21-22]分析了优化动平台运动轨迹，表明能减少冗余驱动机构功耗。

本文对平面3自由度4-PRR冗余并联机构进行运动学与动力学求解，提出驱动力二范数与最小驱动总功率优化方法并对此机构功率进行优化，由驱动功率得到机构运动周期内功耗，与非冗余驱动并联机构进行对比，得到冗余驱动优化方法的优化特征。

1 机构模型描述与运动学逆解

1.1 机构模型描述

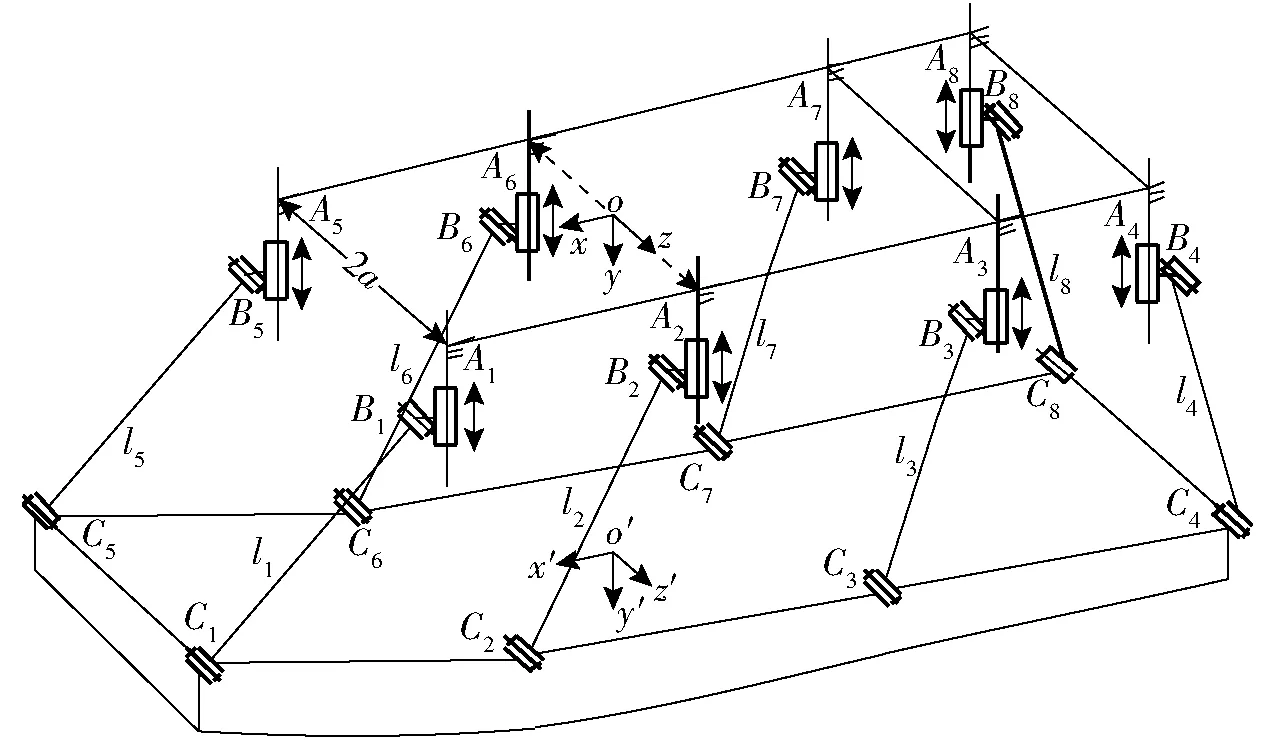
图1 8-PRR/6-PRR并联机构结构简图Fig.1 Schematic of 8-PRR/6-PRR parallel mechanism

喉块段驱动实际结构如图1所示，主要由喉块、固定基座及连接两个平台的拉杆构成。机构共有4组8条运动支链，每条分支包含相同的运动部件和运动副，每条支链由1个滑块导轨移动副P和2个转动副R组成，移动副P为驱动副。将8-PRR冗余驱动并联机构的第3条和第7条支链移除即得到非冗余驱动的6-PRR并联机构。

由于此机构为1R2T三自由度机构，且关于xoy平面对称，为便于分析，机构简化为平面4-PRR冗余驱动并联机构，如图2所示。将4-PRR冗余驱动并联机构的第3条支链移除即得到非冗余驱动的3-PRR并联机构。

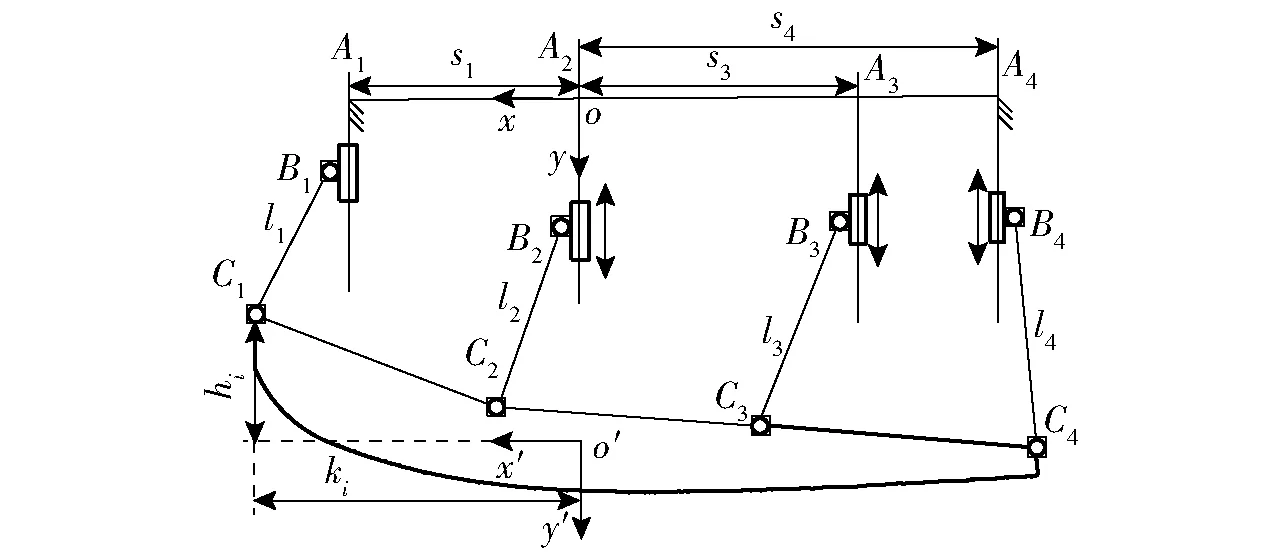
图2 4-PRR并联机构结构简图Fig.2 Schematic of 4-PRR parallel mechanism

在基座A2建立定坐标系oxyz，在喉块质心处建立动坐标系o′x′y′z′。各移动副之间的轴线距离为si，拉杆长度为li，下铰链点Ci到平面x′z′的距离为hi, 下铰链点Ci到平面y′z′的距离为ki。其中C1、C2、C3在y′轴的负方向，C4在y′轴的正方向。第i条支链的封闭矢量图如图3所示。其中，si为移动副轴线在定坐标系中沿x轴的位置矢量，ei为移动副驱动方向单位矢量，ni为上铰链点到移动副轴线的距离矢量，ui为拉杆的单位方向矢量，ci为下铰链点到动坐标系原点的矢量。

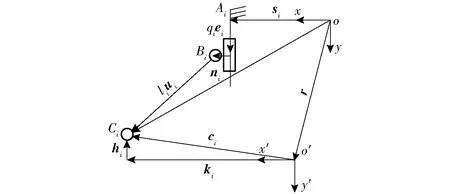
图3 第i条支链封闭矢量图Fig.3 Vector diagram of the ith PRR kinematic chain

如图2、3所示，动平台的位姿可由一个位置矢量r和一个旋转矩阵oRo′描述。动平台绕定坐标系z轴旋转角为θ，则位置矢量r和动坐标系相对于参考坐标系的旋转矩阵oRo′分别为

(1)

(2)

1.2 运动学求解

平面4-PRR冗余驱动并联机构和3-PRR并联机构的运动学求解方法相同，本节以4-PRR关联机构为模型进行求解。

1.2.1位置逆解

如图3所示，建立位置封闭矢量方程

(3)

则该机构的位置逆解模型为

(4)

将已知结构参数条件代入式(4)，得到4条驱动支链的位置逆解表达式为

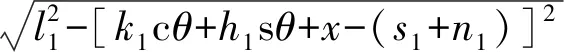
(5)

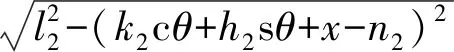
(6)

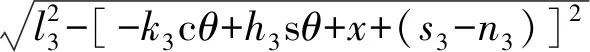
(7)

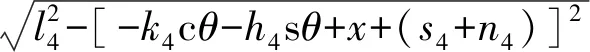
(8)

其中sθ表示sinθ，cθ表示cosθ。

1.2.2雅可比矩阵及速度求解

求解并联机构的雅可比矩阵一般使用微分变换法或者矢量积法。针对该冗余并联机构采用基于符号运算的微分变换法，求出一阶影响系数矩阵，并采用一阶运动影响系数对该机构速度雅可比矩阵快速求解。

滑块位置可以表示为

(9)

将式(9)对时间求导,得到滑块速度为

(10)

即得到该机构末端速度与驱动速度的映射关系为

(11)

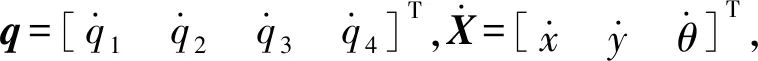
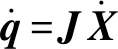
(12)

其中

J——雅可比矩阵，机构的一阶影响系数矩阵

对于3-PRR并联机构，雅可比矩阵为3×3的方阵。

1.2.3加速度求解

机构运动影响系数反映了机构的运动学和动力学本质。本文利用机构的二阶运动影响系数求解滑块加速度。

将式(10)对时间求导表示为

(13)

式中Hi——二阶影响系数矩阵

由式(13)求解得驱动加速度

(14)

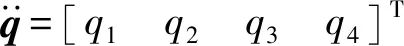
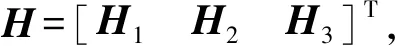
2 动力学建模

动力学建模方法主要包括牛顿-欧拉法、凯恩法、拉格朗日功能平衡法以及虚功原理法。虚功原理建模方法在执行效率和算法上更为出色。本文采用虚功原理进行冗余并联机构及其非冗余并联机构的动力学模型建模。由于拉杆的质量相对于动平台、滑块及推杆的质量较小，转动惯量也较小，把拉杆质量转换到动平台和滑块质量上。

动平台在风洞流场中做平面运动，为便于分析，将其扩展到空间运动。对于动平台，外力、惯性力和重力合力为

(15)

式中mp——动平台、下铰链及每根拉杆一半质量的质量和

fe——作用于动平台的外力

ne——作用于动平台的外力矩

wp——动平台角速度

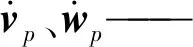
oIp——动平台在定坐标系下的惯性张量

对支链i的滑块及推杆，只有平动，则作用在滑块上的驱动力、惯性力和重力合力为

(16)

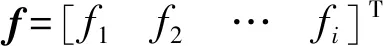
式中mqi——第i条支链上滑块、推杆、上铰链及一半拉杆的质量和

N——滑块惯性力

Ni——第i条支链上的惯性力

f——滑块驱动力

fi——第i条支链上的驱动力

由式(15)、(16)可得，虚功原理可描述为

(17)

其中

δxp=[δxpδypδθp]T

式中 δxp——动平台虚位移

δq——驱动虚位移

式(17)中，虚位移δxp与δq满足机构关节的约束，其关系为

δq=Jδxp

(18)

将式(18)代入式(17)得

(19)

式(19)对任意的δxp均成立，因此有

Fp+JTf+JTN=0

(20)

其中

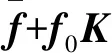
(21)

(JT)+=J(JTJ)-1

f0=(E-(JT)+JT)

式中 (JT)+——JT的广义逆矩阵

f0——JT的零空间基向量

K——JT的零空间基向量系数

E——单位矩阵

对于3-PRR非冗余并联机构，(JT)+为JT的逆矩阵，f0不存在。对于4-PRR冗余并联机构，式(21)有4个未知数、3个线性方程，故解不是唯一的；对于3-PRR非冗余并联机构，解是唯一的。

3 驱动输入功率分析

对3-PRR非冗余并联机构的输入功率进行分析；并利用驱动力的二范数解、周期内功耗最小两种方法分别对4-PRR冗余并联机构的输入力、功率进行优化分析。

3.1 3-PRR非冗余并联机构驱动功率

对于3-PRR非冗余并联机构，其输入驱动力和驱动功率为

f=-(JT)-(Fp+JTN)

(22)

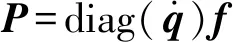
(23)

其中

3.2 4-PRR冗余并联机构驱动功率

对于4-PRR冗余并联机构，分别利用驱动力的二范数解和最小驱动总功率两种方法求解。

3.2.1驱动力二范数解

对该冗余并联机构，驱动力配置方式有无穷多种，利用驱动力二范数解，式(21)可写为

f=-(JT)+(Fp+JTN)

(24)

驱动功率

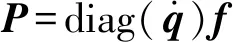
(25)

其中

即为4-PRR冗余驱动并联机构驱动力二范数解得的驱动器输出功率。

3.2.2最小驱动总功率解

由式(21)可得，驱动功率为

(26)

其中

对于第i个驱动器，虽然输出功率在一个周期内有正负，其输出功总是正的，故在由功率对时间在一个周期内积分时，应该对功率取绝对值，即

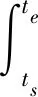
(27)

式中ts——开始时间te——结束时间

则，一个周期驱动器总的输出功

由式(26)可知,瞬时输出功率解不唯一，为使一个周期内输出功最少，则瞬时输出总功率应该最小，瞬时输出总功率为

Ps=|P1|+|P2|+|P3|+|P4|

(28)

其中，Ps为关于零空间系数K的非线性函数。当Ps取得最小值时，将K代入式(21)、(26)即得到驱动器瞬时输出总功率最小时的驱动力与输出功率。

对每个驱动器，其输出功率最大不能超过其额定功率，利用Matlab中的工具箱文件fmincon求解有约束的非线性最小值Psmin。通过得到有限个时间点的最小功率来逼近理论上的最小功率变化。其将t时刻的基向量系数返回值kj作为t+Δt时刻的初值循环求解Psmin，流程如图4所示。

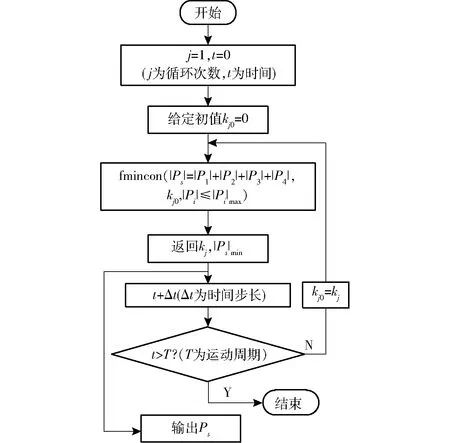
图4 最小功率变化仿真流程Fig.4 Flow chart of minimum power’s simulation

3.3 周期内驱动器输出功

对冗余和非冗余并联机构，驱动器总的输出功率为

Ps=|P1|+|P2|+…+|Pi| (i=3或4)

(29)

则一个周期内总的输出功为

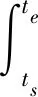
(30)

一个周期内驱动器输出功率W近似求解计算方法为

(31)

其中

式中n——时间间隔数

tk——一个时间间隔的起始时刻

tk+1——一个时间间隔的结束时刻

4 数值模拟分析

综合分析风洞试验条件及并联机构的实际要求，该并联机构参数如表1所示。

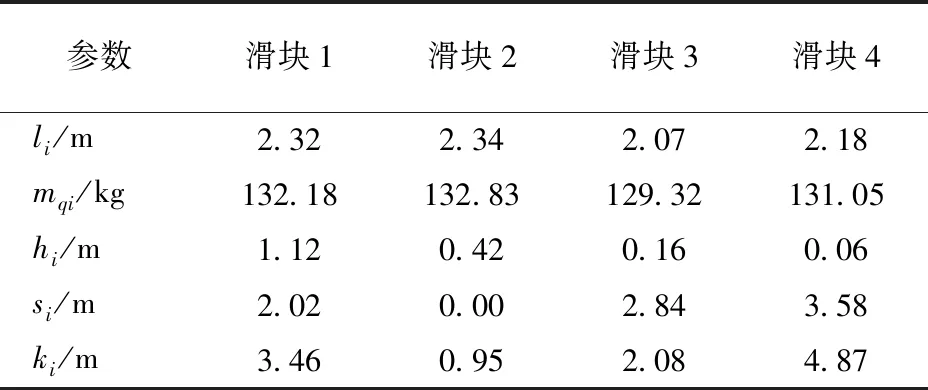
表1 并联机构结构参数Tab.1 Geometrical parameters of parallel manipulator

动平台的质量为12 547.33 kg，其在动坐标系中的惯性张量矩阵为

其在定坐标系中的惯性张量为

oIp=oRo′o′Ipo′Ro

在动坐标系中，作用于动平台的外力为

则在定坐标系中外力为

根据该并联机构在风洞中的状况，选择一种典型工况进行刚体动力学与能耗分析，其运动轨迹为

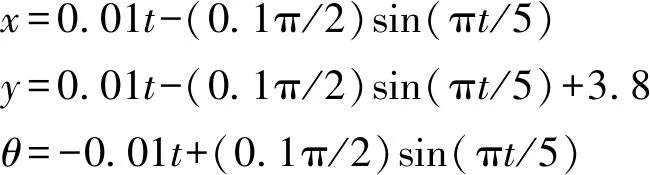
由式(11)和式(13)得到滑块速度与加速度曲线如图5、6所示。

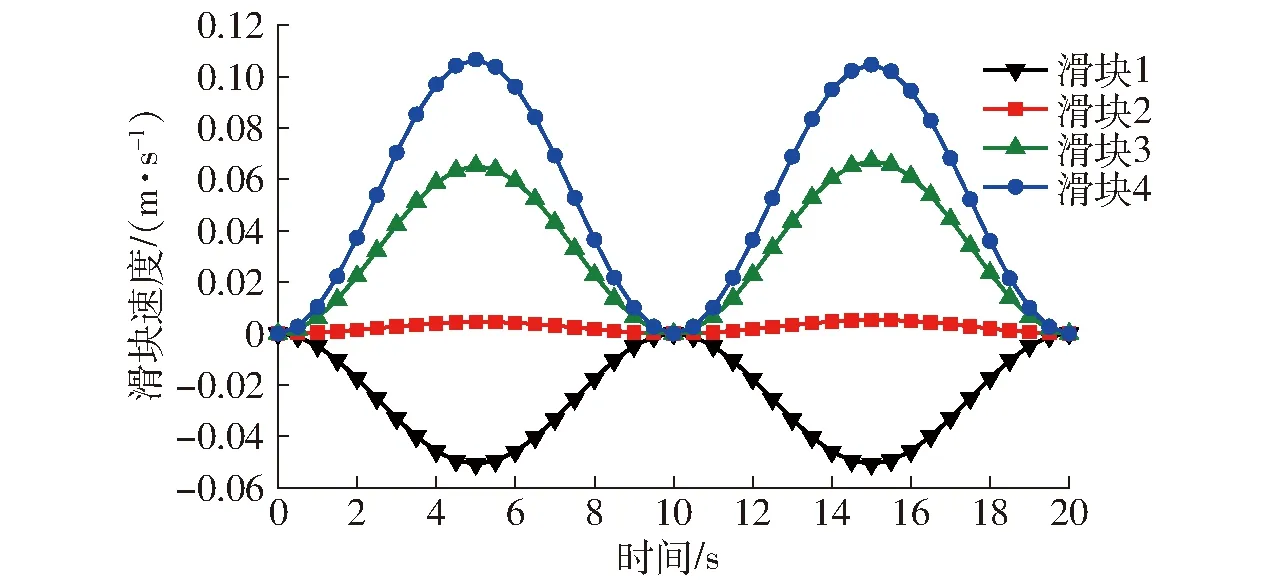
图5 滑块速度曲线Fig.5 Velocity curves of sliders

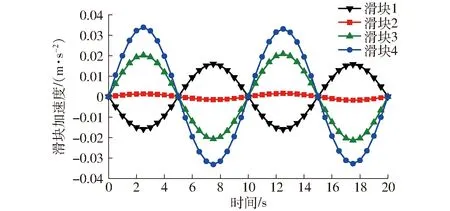
图6 滑块加速度曲线Fig.6 Acceleration curves of sliders

由图5和图6可得，机构最大速度和加速度都出现在滑块4，分别为0.107 m/s和0.033 9 m/s2,即最大位移也出现在滑块4。

图7 驱动力仿真结果Fig.7 Simulation results of driving forces

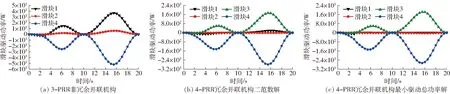
图8 驱动功率仿真结果Fig.8 Simulation results of driving power

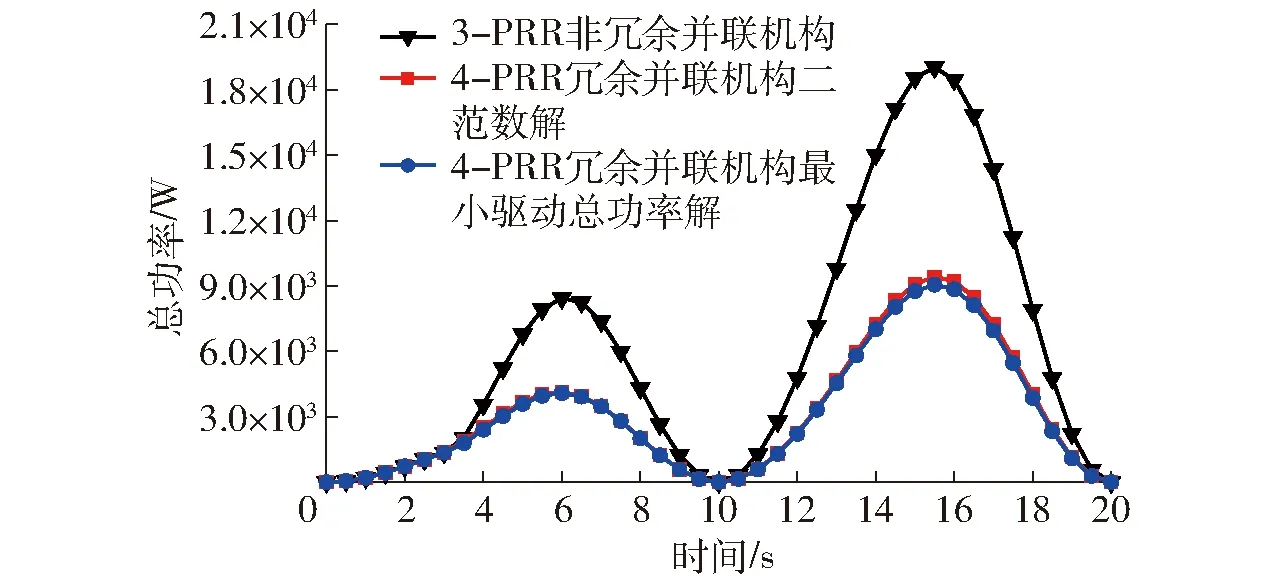
图9 总功率仿真结果Fig.9 Simulation results of sum of driving power

由式(22)、(24)、(21)得到驱动力仿真结果如图7所示。由式(23)、(25)、(26)得到驱动功率仿真结果如图8所示。由式(31)可得，非冗余并联机构、冗余并联机构驱动力二范数解和冗余并联机构最小驱动总功率解在一个周期内的驱动器输出总功率及总功分别如图9和表2所示。

对于3-PRR并联机构对应的6-PRR并联机构，总功为6个驱动器做功之和；对于4-PRR并联机构对应的8-PRR并联机构，总功为8个驱动器做功之和。

表2 驱动器输出总功Tab.2 Total output power of driver J

从图7可看出，在运动周期内，3-PRR并联机构最大驱动力出现在滑块2，最大驱动力为145.1 kN。由驱动力二范数解和最小驱动总功率解得到的4-PRR冗余驱动并联机构最大驱动力相比于3-PRR并联机构最大驱动力都明显减小，4-PRR冗余驱动并联机构驱动力二范数解最大驱动力出现在滑块3，为33.4 kN；4-PRR冗余驱动并联机构最小驱动总功率解最大驱动力出现在滑块3，为35.6 kN。4-PRR冗余驱动并联机构滑块3和滑块4起主导作用，两者的驱动力明显大于滑块1和滑块2；4-PRR冗余驱动并联机构最小驱动总功率解存在异常驱动，在3.5～20 s内，仅电机2、3、4起到驱动作用，其产生的原因是4-PRR冗余驱动并联机构的功耗被作为优化模型，并且该优化模型仅与功率的绝对值有关，即为驱动力的绝对值函数。

从图8可以看出，在运动周期内，3-PRR并联机构最大驱动功率出现在滑块4的15.5 s处，为-5 200.9 W(负功)；冗余驱动并联机构最大驱动功率明显减小，4-PRR冗余驱动并联机构驱动力二范数解最大驱动功率出现在滑块4，为-2 788.5 W(负功)；4-PRR冗余驱动并联机构最小驱动总功率解最大驱动功率出现在滑块4，为-2 665.4 W(负功)。冗余驱动滑块3和滑块4的驱动功率远大于滑块1和滑块2的驱动功率。

由图9和表2可知，冗余驱动并联机构电机输出总功明显减少，分别减少到64 232 J和62 321 J，分别减少49.2%和50.7%；4-PRR冗余驱动并联机构最小驱动总功率解做功略小于驱动力二范数解做功。

5 结论

(1)建立了4-PRR冗余并联机构及其非冗余3-PRR并联机构的运动学逆解模型，根据坐标变换和结构特点得到运动学逆解和机构雅可比矩阵，利用二阶影响系数法求解了加速度模型，为动力学分析提供了基础。

(2)利用虚功原理构建了机构动力学模型，提出以并联机构运动周期内驱动器做功为优化目标，求解了3-PRR非冗余并联机构及其4-PRR冗余并联机构驱动力二范数解、最小驱动总功率解的滑块驱动力和和驱动功率。

(3)冗余驱动并联机构能够有效减少运动周期内驱动器做功，其中驱动力二范数解与最小驱动总功率解的驱动器做功差异较小，且驱动力二范数解不存在驱动奇异，故能够在均衡驱动力上有效减少驱动器做功。

(4)冗余并联机构与非冗余并联机构的驱动力与功率仿真结果表明，驱动力二范数解与最小驱动总功率解所做总功分别减少49.2%和50.7%。