冗余驱动并联机构动力学模型TVC优化H∞鲁棒控制
王启明 苏 建 高大威 吕志超 宗高强
(1.上海理工大学机械工程学院, 上海 200093; 2.吉林大学交通学院, 长春 130022; 3.同济大学汽车学院, 上海 201804)
0 引言
由列车提速、货运重载及轨道不平顺等引起的车辆振动现象愈加明显,直接影响了车辆运行平稳性及乘客乘坐舒适性。开展多源激励下冗余驱动并联机构机电耦合动力学建模及协同控制机理研究对于研发高精度、高性能的检测试验装备[1],实现对车体及车端各部件性能参数检测具有重要意义。
冗余驱动并联机构由于具有高精度、无累积误差、动态响应快、高负载、高刚度等优点,已被广泛应用于航空航天[2]、轨道车辆[3]、地震模拟器[4]及并联机床[5]等领域。并联机构处于低速运动时,其动力学性能表现不明显,伺服系统无论跟踪铰点关节空间激振器的位移驱动信号,还是任务空间的自由度驱动信号,均能满足精确跟踪控制要求。而具有高负载、高刚度、抗倾覆性能的冗余液压驱动并联机构被用于高频振动试验台时,其非线性动力学特性凸显,且各关节的耦合关系不能忽略。并联机构的控制精度决定了试验台对车辆及各部件结构力学和动力学参数的检测精度。
经典动力学控制主要包括增广PD控制[6]和计算力矩控制[7]。文献[6-13]研究了并联机构的动力学控制器。文献[6]等以6-DOF并联机构为例,提出了考虑重力补偿的PD控制器,在一定程度上消除了稳态误差。KIM等[8]以Stewart机构为例,提出了鲁棒非线性控制器。文献[9-10]提出了基于频域的模态解耦控制,其难点在于质量矩阵和刚度矩阵的确定。魏巍等[11]以超冗余度振动台为例,采用零位自由度线性化控制时的系统传递函数,通过模态矩阵变换后,将三状态反馈引入模态空间进行控制。吕文斌[12]对冗余驱动并联机构内力成因和内力解耦控制[13]进行研究,利用内力空间矩阵的任意一组基底和各激振器处理,推导内力反馈控制向量。
本文以转向架参数测定试验台(Test bench for bogie parameters,TBBP)为例,针对冗余驱动并联机构控制系统设计未考虑动力学建模及伺服阀动、静态特性等问题,基于第二类Lagrange方程和流体力学动力学,对动平台及液压系统中机械、液压系统建模,建立电液伺服系统五阶传递函数模型,通过主导能量最优模型将其降为三阶模型。以此为控制对象提出基于三矢量控制(Three vector control,TVC)反馈优化的H∞鲁棒控制策略(TVC-ROB),并与TVC前馈反馈控制、TVC反馈优化的模糊自适应PID控制(TVC-FAPID)两种控制策略在阶跃信号、线性扫频、实际武广谱路谱复现等进行对比分析。
1 冗余驱动并联机构描述
转向架参数测定试验台是一种双冗余驱动并联机构,主要用于测定整车、转向架、车端及各部件的结构力学和动力学参数。如图1所示,每个冗余驱动并联机构均由4个垂向激振器、2个纵向激振器和1个横向激振器支撑运动平台构成。每套电液伺服激振器的两端均通过消隙球铰连接。建立机构坐标系如图1所示。
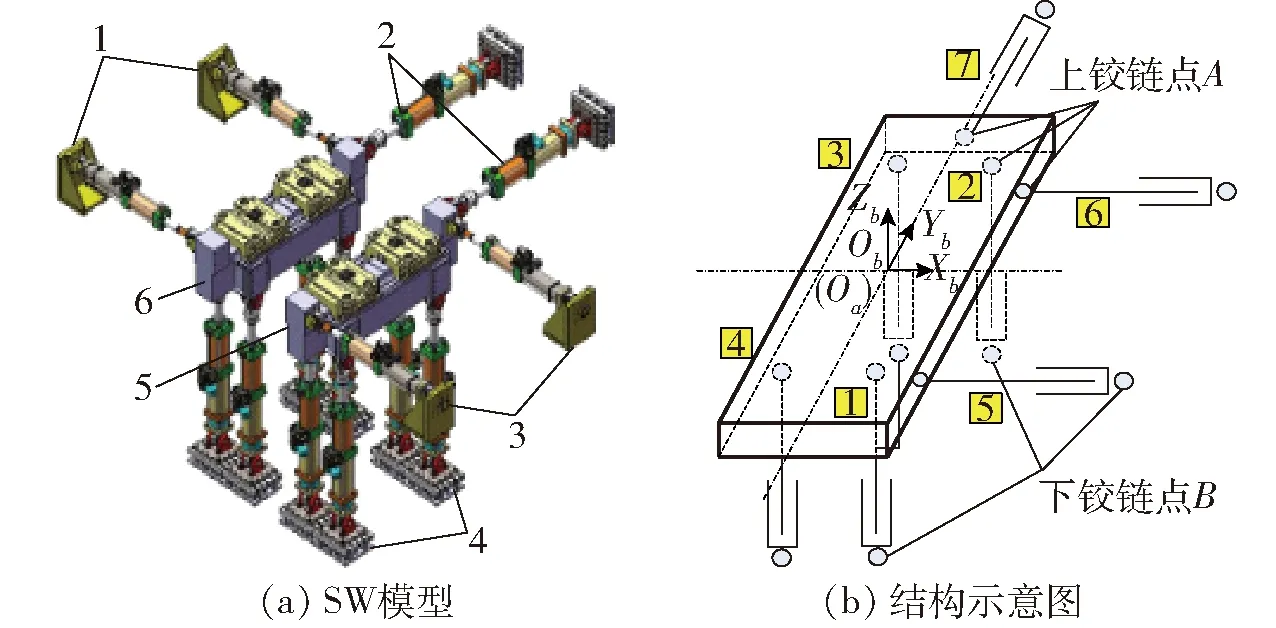
图1 转向架参数测定试验台Fig.1 Test bench for bogie parameters (TBBP)1、3.纵向激振器 2.横向激振器 4.垂向激振器 5.前六自由度运动平台 6.后六自由度运动平台
2 冗余驱动并联机构动力学模型
建立系统输入、参数与状态三者之间的系统动力学方程。本文考虑模型正交对称、低高频运动等特点,采用第二类Lagrange方程对并联机构运动平台、液压伺服动力机构及整体系统进行动力学建模。
2.1 基于Lagrange方法的动平台动力学模型
为了简化建模过程和方便计算,先作如下假设:平台质心与坐标系原点重合,忽略各连接机构的摩擦力,整个平台质量分布均匀,机构内部各个关节的约束力均为理想约束力,利用拉格朗日方程建模只需用广义坐标将系统的动能和势能表示,并求出非保守的主动力系的广义力,即可建立系统动力学模型。将平台看作一个整体,可得平台Lagrange方程为
(1)
式中τ——系统所受合力
动平台系统动能为
(2)
式中mp——平台质量
v——平台线速度矩阵
ωJ——平台旋转速度矩阵
Jp——平台旋转惯量矩阵
动平台在运动过程中相对于惯性坐标系可实现沿X、Y、Z轴向的平移运动以及绕三轴的旋转运动,因此平台运动可描述为
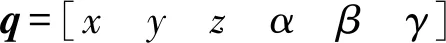
(3)
选取ADAMS中常用的绕X-Y-Z的顺序进行旋转,绕X轴旋转α,再绕新的Y轴旋转β,最后绕新的Z轴旋转γ,则广义坐标变换矩阵为
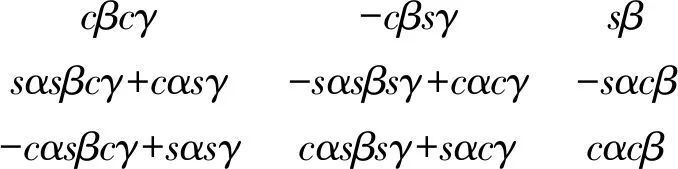
(4)
式中,c代表cos,s代表sin。
根据角速度合成定理可知平台旋转速度矩阵为
(5)
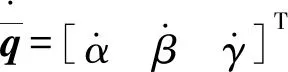
式中W——欧拉转角到角速度矢量的变换矩阵
分析平台旋转顺序、旋转轴以及各个旋转角度可得
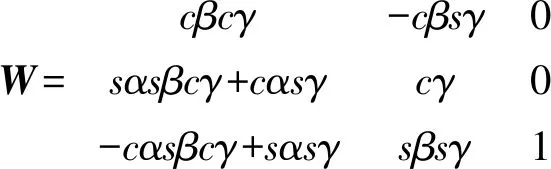
(6)
将式(3)~(6)代入式(2),进一步化简为
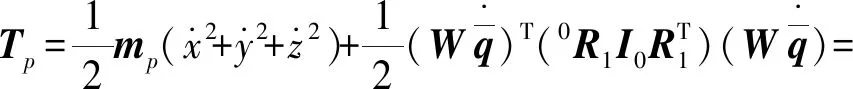
(7)
式中I0——动平台相对于原始坐标系的转动惯量
考虑平台为均匀分布长方体,则可知
(8)
式中a、b、c——运动平台沿X、Y、Z轴向长度
则平台的动能最终为
(9)
(10)
式中Mp——平台的整体惯性矩阵
2.2 液压驱动系统动力学模型
2.2.1液压动力机构
并联机构由4个垂向激振器和3个水平激振器支撑运动平台构成,考虑平台运动特性,采用第二类Lagrange方程对垂向、水平液压激振动力机构建模,系统动力学方程满足
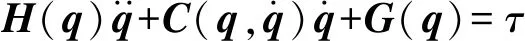
(11)
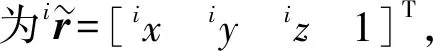
(12)
式中0Ai——系O坐标向系i坐标的变换矩阵
若将该点的齐次速度定义为
(13)
此时第i级的动能为
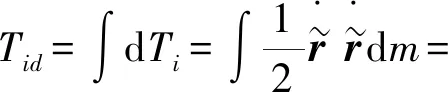
(14)
其中
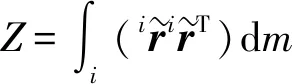
则此时多级系统总动能为
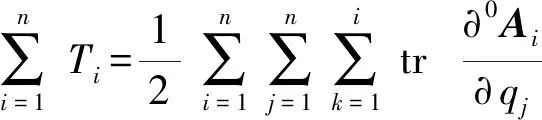
(15)
该系统转换矩阵为
继续化简得
(16)
由式(12)~(16)可确定系统动力学方程系数矩阵分别为
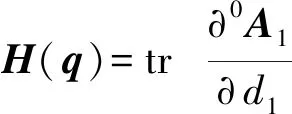
(17)
(18)
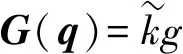
(19)
则系统动力学模型为
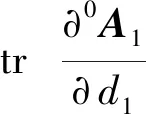
(20)

对液压缸进行受力分析可得
(21)
式中F——液压缸输出驱动力
fζ——液压杆粘性摩擦力

kζ——电磁块的滑动摩擦因数
将式(21)代入式(20)可得液压动力机构动力学方程为
(22)
2.2.2液压缸动力学方程
液压缸伺服系统主要采用对称阀控制对称液压缸形式的动力机构,根据四通滑阀流量方程可得液压缸的流量连续性方程如下
(23)
由于滑阀对称匹配,则通过滑阀节流口流量亦相等,因此在动、静态情形下ps=p1+p2,由于pL=p1-p2,得
(24)
(25)
式中Ctp——液压缸泄漏系数,m5/(N·s)
由2.2.1节和2.2.2节可知液压系统动力学方程
(26)
其中
2.3 电液伺服系统传递函数确定
为了保证建模的准确性,在2.2节液压系统动力学建模的基础上,考虑伺服阀的动态特性,得到各自动力学方程进行S域变换求取传递函数作为控制对象。由于伺服阀与液压动力机构是时域上的串联机构,因此在S域上即为传递函数的乘积关系,最终确定电液伺服系统传递函数。
如图2所示,对电磁线圈中的滑动活塞进行受力分析可得
(27)
式中mmass——电磁线圈中铁块的质量
Fspool——滑阀所受合力
kspring——电磁铁中回位弹簧的弹性系数
xv——伺服阀阀芯位移
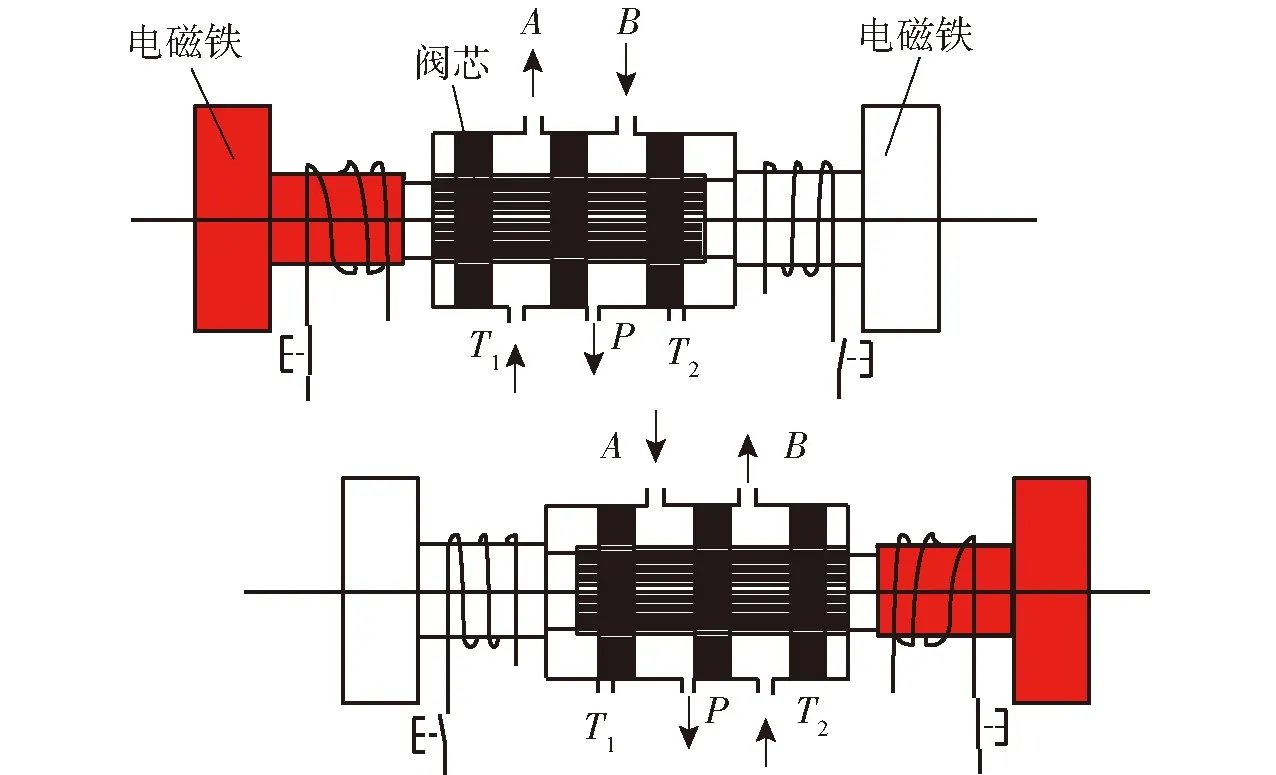
图2 电磁阀工作原理图Fig.2 Operational principle diagram of solenoid valve
将伺服阀动力学方程S域变换后可得考虑其动态特性的传递函数为
(28)
式中S——滑动活塞面积
将式(28)转换为标准二阶系统为
(29)
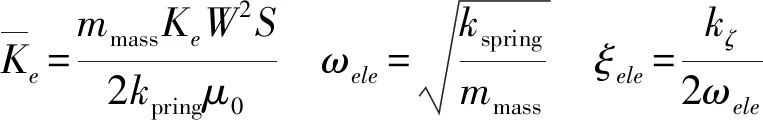
式中Ke——位移反馈信号控制输入电流的增益
而液压系统传递函数如下
(30)
由于时域上的串联机构,在S域为乘积关系,因此可得电液伺服系统传递函数为
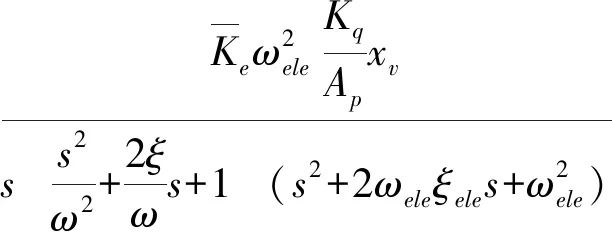
(31)
2.4 基于主导能量最优模型的主导极点降阶
一般根据实际系统建立的数学模型,尤其是大系统的数学模型,其状态方程的维数或者传递函数[14]阶数往往很高,使得系统分析和控制器设计较为困难。因此本文提出一种基于主导能量最优模型[15]的方法对系统进行降阶,尽可能逼近原系统本征结构、马尔科夫参数、时间矩及脉冲响应能量等主要特征。降阶法主要为理论降阶法和实际降阶法,本文属于理论降阶法的一种。
2.4.1主导极点确定
线性定常系统传递函数为
(32)
将其变形为留数累加形式
(33)
式中μi——系统特征值
hi——特征值对应的留数
则系统对单位脉冲的响应为
(34)
通过对系统输入满足式(35)统计特性的白噪声方式为系统的每个模态进行加权处理。
E[z(t)z(t-τ)]=σ2δ(τ)
(35)
式中σ2——信号方差
δ(τ)——狄拉克δ函数
则系统对输入白噪声信号的响应为

(36)
将输出信号的自相关函数v(τ)=E[y(t)y(t-τ)]代入系统的单位脉冲响应中化简可得
(37)
其中
式中dj——自相关函数的系数
其可表征μj代表的模态对系统输出y(t)贡献的能量。dj的相对大小可由相对函数表示为
(38)
2.4.2模型最优降阶方法
利用相对函数Δj确定主导极点之后,省略掉非主导极点,则降阶后传递函数有如下形式
(39)
根据式(37)可得降阶后模型的自相关函数的系数为
(40)
式中μdi——降阶后的主导极点
hdi——降阶后主导极点对应的留数
降阶后传递函数的分母系数由主导极点获得,而其分子系数和乘子λ则由下述方法求得。
根据降阶前后系统特性和响应尽量接近的原则,及降阶后的极点对输出的贡献应与原系统主导极点对输出贡献尽量接近的原则,可定义目标函数
(41)
原系统能量函数为
(42)
降阶后能量函数为
(43)
两能量间的关系可表示为
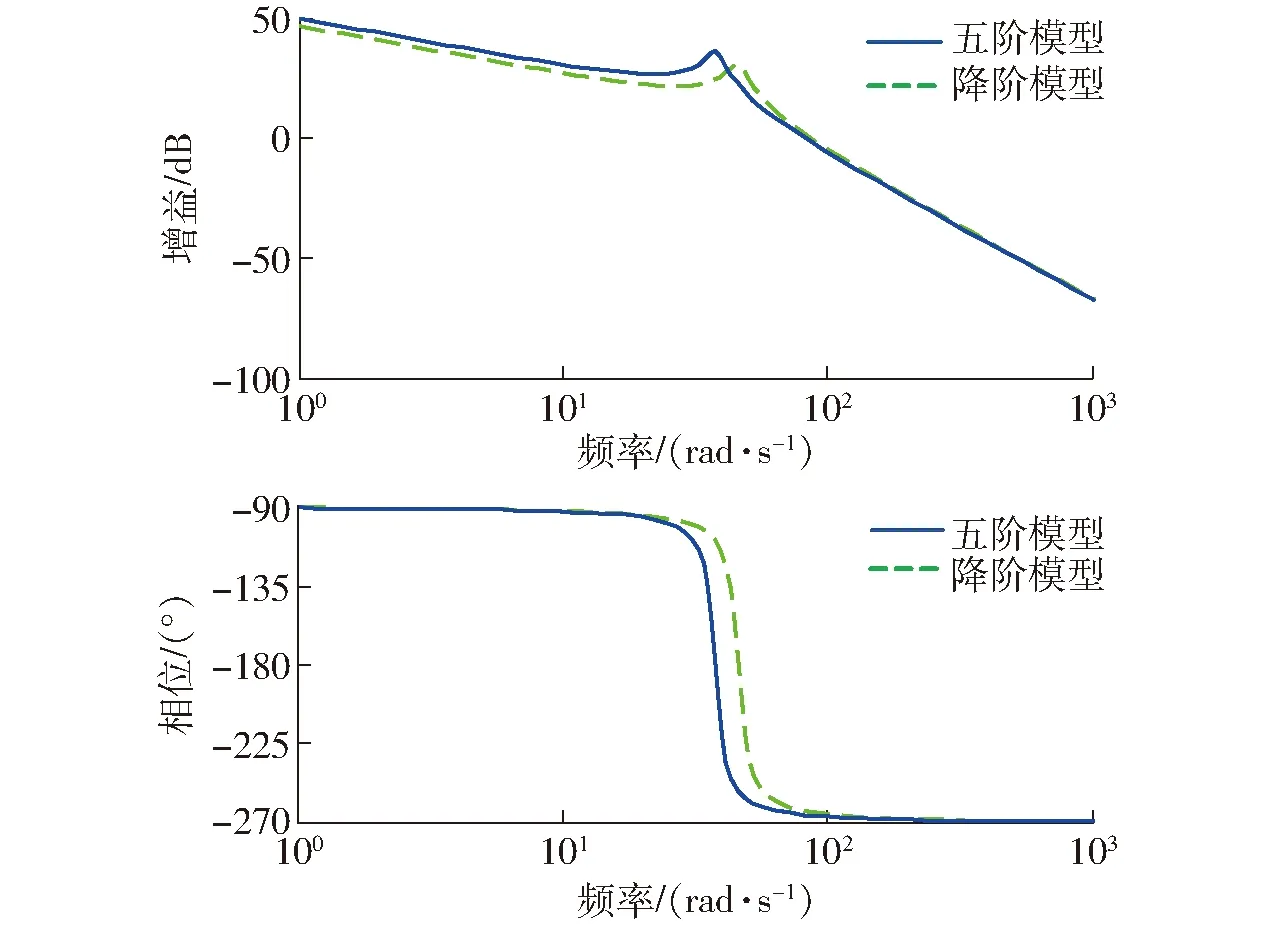
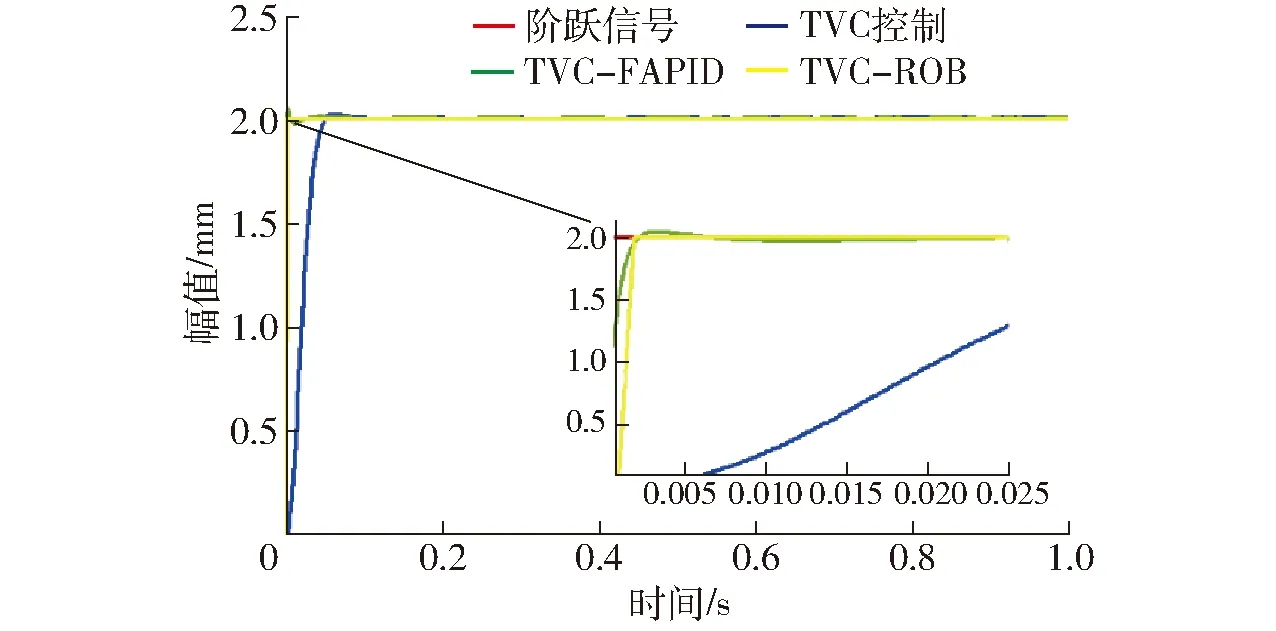
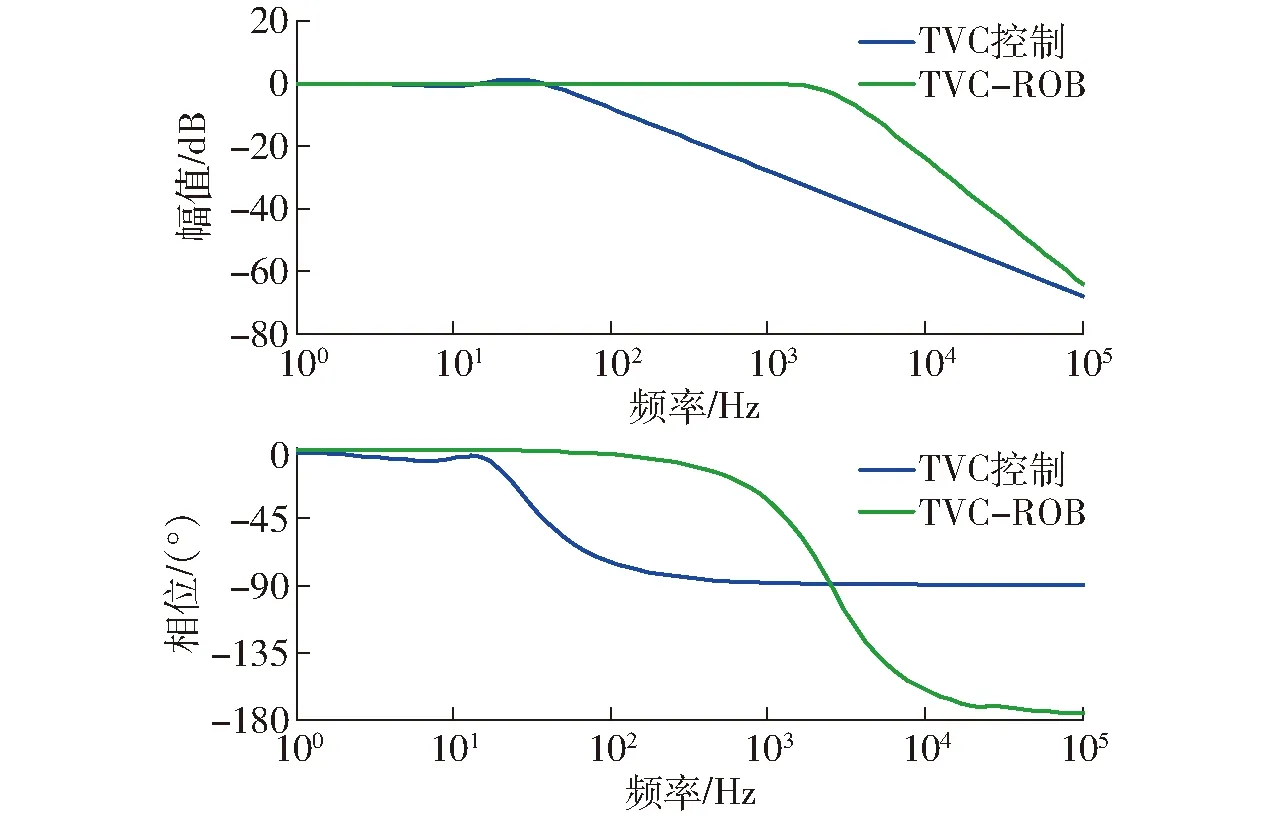
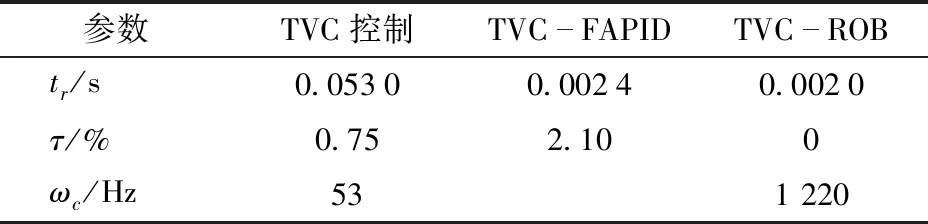
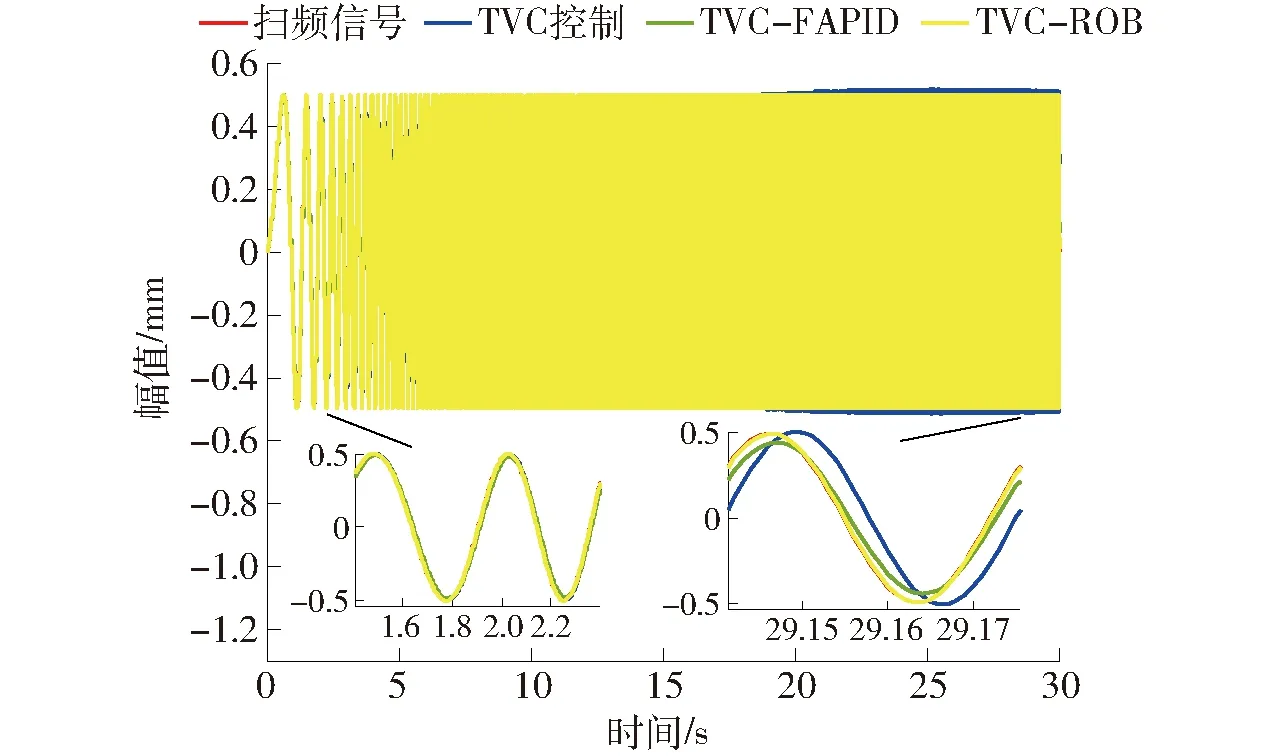
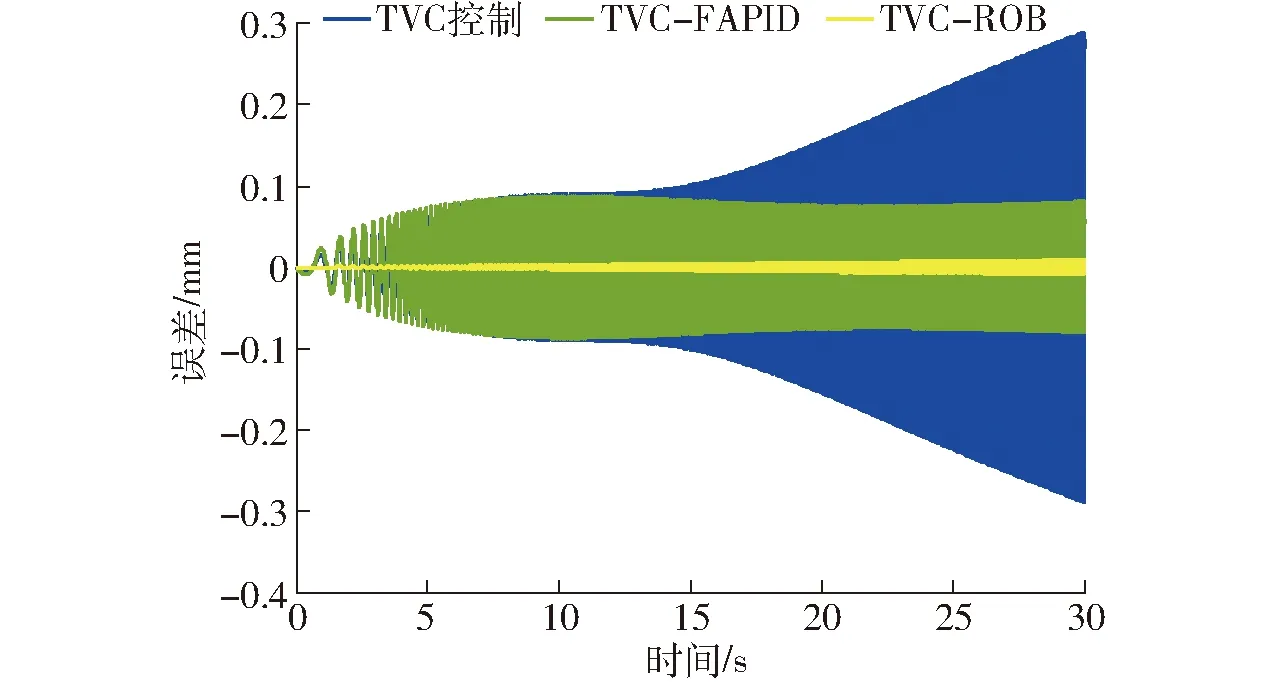
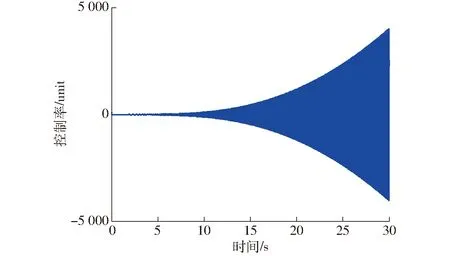
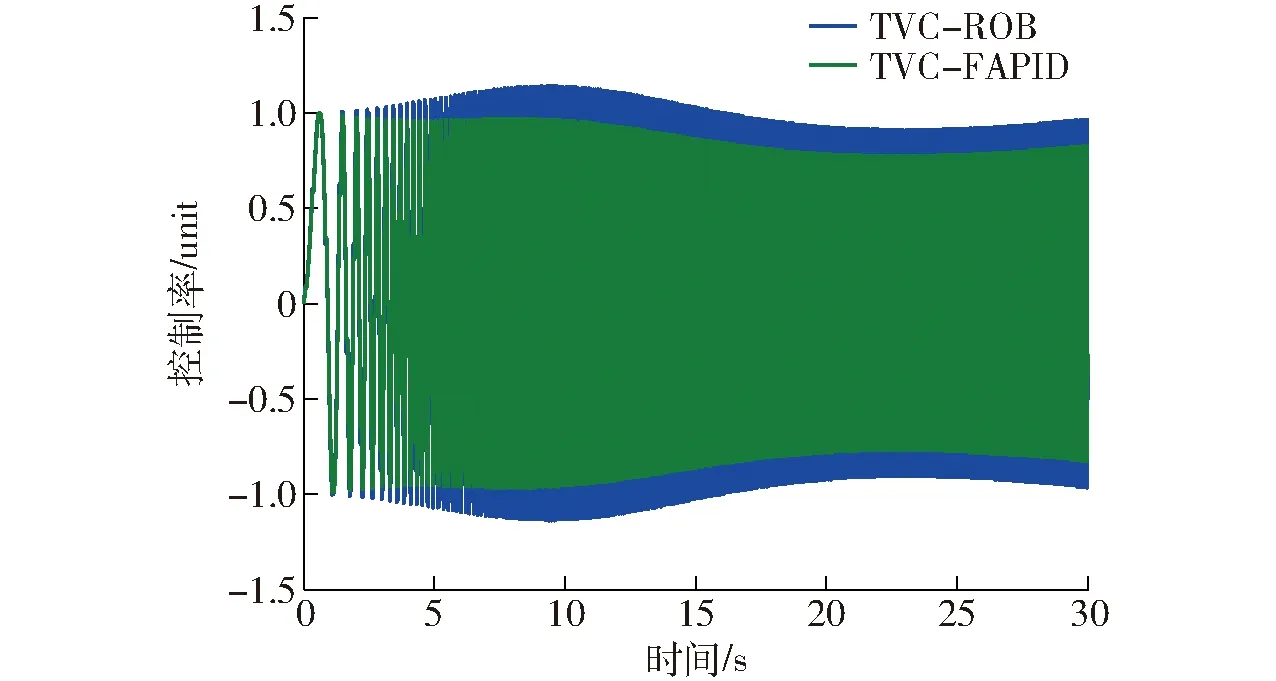
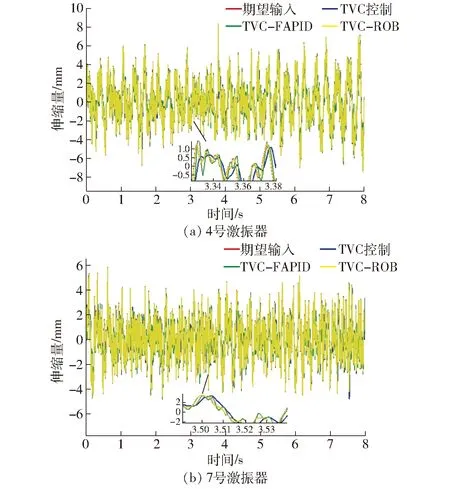
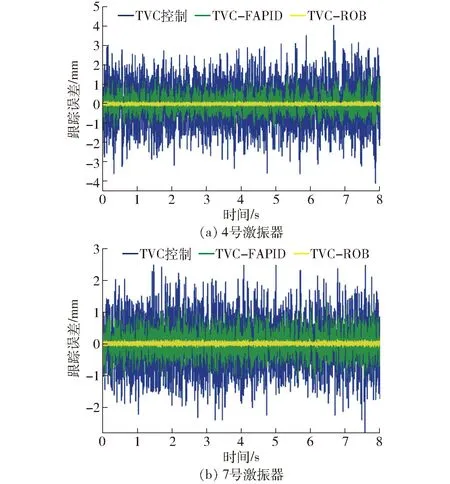
Ed=kE(0 (44) (45) 将式(41)~(44)代入式(45)可得 (46) 式中λ——拉格朗日算子 (47) (48) 系统模态特征值和极点能量贡献百分比值如表2所示,降阶后系统模型参数如表3所示。 表2 降阶后的系统模态分析Tab.2 Model analysis of reduced-order system 表3 降阶后模型参数Tab.3 Model parameter of reduced-order system 对降阶后系统采用劳斯判据可知,系统稳定,且需注意虚轴上的极点可导致系统临界稳定状态。 2.4.3降阶前后模型对比分析 如图3所示,利用主导极点进行系统降阶后,系统的幅频、相频响应在变化趋势上基本与未降阶一致,而谐振峰幅值和频率略有不同、相位稍有滞后。通过对比五阶系统的谐振峰和谐振频率修正三阶模型参数,验证了本节提出的基于主导能量最优模型降阶法的有效性。降阶到较易处理的阶数,便于后续动力学控制。 图3 降阶系统与原系统开环动态特性对比Fig.3 Comparison of open-loop dynamic characteristics between reduced-order system and original system 图4 加入TVC反馈控制系统方框图Fig.4 System block diagram adding TVC feedback control 加入TVC反馈控制系统如图4所示,主要是对试验台或液压动力机构位移、速度、加速度3个状态的综合反馈控制。通过在位置闭环传递函数中引入加速度和速度反馈提高系统液压动力机构的阻尼比和固有频率,从而优化系统的动态性能,保证系统在稳定条件下拓展频宽。 结合电液伺服试验台的特性,认为满足实际工况需求的试验台可由典型传函[16]描述为 (49) 式中k——系统相对增益 ω1——系统阶跃响应时间对应的响应频率 ω2一般取1.07倍的自然频率,ζ2一般取0.7。 通过对比降阶传函与典型传函形式,可将其近似成三阶模型,即 (50) 式中kRO——优化后的系统相对增益 ωRO——优化后的系统固有频率 ζRO——优化后的系统阻尼比 在控制对象基础上,引入TVC反馈后系统传函为 (51) 通过比对满足实际工况的电液伺服试验台的典型传函式(50)与引入TVC反馈后的系统传函式(51),可知TVC反馈系数分别为 (52) 经计算可知,krd=60,kra=0.008 4,krv=1.26。 TVC反馈控制策略提高了系统性能,但当激励信号为随机信号、高频信号时,系统输出出现较大的跟踪误差,且相位也存在滞后。因此在TVC反馈控制优化系统基础上提出具有高跟踪性能、良好抑制扰动和抗噪能力的H∞鲁棒控制器[17]。H∞控制理论核心思想是针对存在不确定性因素的闭环系统控制器使其稳定,也就是说针对外部有限能量的干扰信号和噪声信号,引入控制器增强闭环系统稳定性且使得干扰和噪声信号对系统期望输出影响最小。有限输入输出能量增益可用传递函数的H∞范数描述。H∞鲁棒控制器设计需将图5a所示标准反馈控制系统框图转换成图5b所示反馈控制增广结构系统。 图5 反馈系统控制框图Fig.5 Control block diagram of feedback system 如图5所示,G为已知的广义被控对象与系统权函数的增广矩阵,K为待设计控制器,w为外部输入信号,包括参考信号、干扰和传感器噪声;z为被控输出信号,包括跟踪误差、调节误差和执行机构输出;u为控制信号,y为测量输出信号,如传感器输出信号等。以系统状态空间方程形式描述任意系统可得 (53) 将式(53)转换为标准增广形式后状态空间方程为 (54) 化简为 (55) 可得响应传递函数矩阵为 (56) 可得 (57) 由图5可得 u=K(s)y (58) 整理式(57)、(58)可得系统输入输出传递函数Twz为 (59) 针对式(59)设计H∞控制器K,使得‖Twz‖∞<γ≤1。需注意基于TVC反馈优化的鲁棒控制器设计主要考虑控制器灵敏度特性,不对权函数进行指定。由式(53)可确定引入TVC反馈后的系统状态空间方程为 (60) 其中 (61) 在不指定权函数基础上将系统进行标准增广转换得到 (62) H∞控制器[18]作为鲁棒控制器的一种,首先需证明其稳定性。当以下条件全部满足时,控制器稳定且存在:①D11足够小,且满足D11<λ。②Riccati方程的解为正定矩阵X。③ Riccati方程的解为正定矩阵Y。④特征值λmax(XY)<γ2。 当上述4个先决条件全部满足时,H∞鲁棒控制器状态方程可表示为 (63) X和Y由Riccati方程式(63)求得 (64) 利用上述4个条件判定控制器存在与否即证明其稳定性,由式(60)~(64)结合系统性能指标设计H∞鲁棒控制器得其状态空间方程为 (65) 其中 (66) 将本文提出的TVC-ROB控制策略与TVC控制、TVC-FAPID控制策略在阶跃响应、开环特性、线性扫频等动态性能方面对比分析。 (1)阶跃响应仿真 结合被控对象以及图6阶跃信号响应及图7频率特性等,得3种控制器动态性能指标结果如表4所示,可知TVC-ROB控制从响应时间、超调量和截止频率都明显优于其他两种控制策略。 (2)线性扫频仿真 对比本文提出的TVC-ROB控制策略与TVC控制、TVC-FAPID控制在0~30 Hz线性扫频时域性能如图8、9所示。随着线性扫频频率的持续增大,3种控制策略的跟踪误差越来越大,尤其是TVC控制在高频30 Hz处误差百分比已达到48.3%,控制器已失效。而控制误差最小的TVC-ROB,在30 Hz处不到1.2%;3种控制策略的控制率如图10、11所示,TVC控制在高频处的控制率较大,达到4 000 unit,而其他两种控制率都在1 unit左右,且上升不明显较稳定。控制率明显增大会引起物理元器件短路、老化加速等问题,应尽量避免。 图6 3种控制策略对阶跃信号响应Fig.6 Three control strategies responded to step signals 图7 两种控制策略的频率特性Fig.7 Frequency characteristics of two control strategies 参数TVC控制TVCFAPIDTVCROBtr/s0.05300.00240.0020τ/%0.752.100ωc/Hz531 220 图8 扫频信号激励下的位移时域跟踪曲线Fig.8 Result of 0~30 Hz linear sweep motion tracking 图9 3种控制策略误差分析Fig.9 Error analysis of three control strategies 图10 TVC控制策略的控制率分析Fig.10 Control rate analysis of TVC control strategy 图11 TVC-FAPID和TVC-ROB控制率对比Fig.11 Contrast of control rate between TVC-FAPID and TVC-ROB 将在实际武广线路谱中采集的水平不平顺、方向不平顺及高低不平顺等信号可转换为动平台绕X轴旋转量、沿Y轴平移量、沿Z轴平移量,再进一步利用位姿反解成7个激振器谱,从而模拟列车在实际武广线路运行状态。 图12 激振器对实际位移信号的时域跟踪曲线Fig.12 Result of actual trajectory tracking 图13 激振器位移跟踪误差分析Fig.13 Error analysis of actual trajectory tracking 选取伸缩运动较为明显的4号和7号激振器,引入3种控制策略后,对比系统对实际位移信号影响。由于实际位移信号中存在高频分量,由图12、13可知,TVC控制对高频信号的跟踪性能较差,其位移跟踪误差百分比最大为43.7%;TVC-FAPID虽通过模糊规则自适应调整系统PID参数使得其高频信号跟踪性能有所改善,但其位移跟踪误差百分比最大为12.5%;本文提出的TVC-ROB控制,在TVC优化系统的基础上引入H∞鲁棒控制,其位移误差百分比仅为1.26%。不仅在高频跟踪性能上改善较为明显,且引入的H∞鲁棒控制,提高了系统抗扰、抗噪性能。 基于第二类Lagrange方程和流体力学,对动平台及液压系统中机械、液压系统进行了动力学建模,同时考虑了伺服阀的动、静态特性,由此建立电液伺服系统五阶传递函数模型,通过主导能量最优模型将其降为三阶模型。以此为控制对象提出了基于TVC反馈优化的H∞鲁棒控制策略(TVC-ROB),并与TVC控制、TVC反馈优化的模糊自适应PID控制(TVC-FAPID)两种控制策略在阶跃信号、线性扫频、实际武广谱路谱等进行跟踪对比分析。结果表明,TVC反馈有效拓展了系统频宽,且提高液压系统阻尼比和固有频率,使得H∞鲁棒控制器对高频信号相位滞后得到补偿,因此TVC-ROB较另外两种控制策略不仅在高频跟踪性能上改善较为明显,其位移误差百分比仅为1.26%,且引入的H∞鲁棒控制,提高了系统抗扰、抗噪性能。高频段TVC-ROB和TVC-FAPID两种策略与TVC控制相比,其控制能量响度大大降低且趋于稳定。TVC控制策略由于其控制器参数整定简单,其有效频段为低频段。

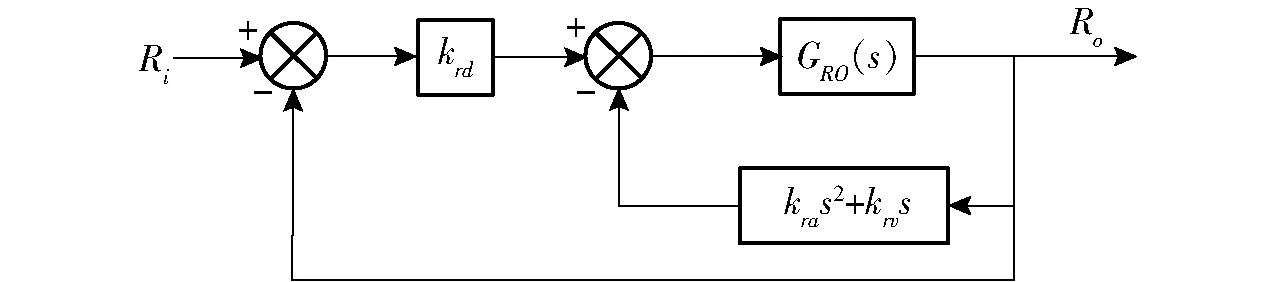
3 控制器设计
3.1 引入TVC反馈控制器
3.2 基于TVC优化的H∞鲁棒控制器设计
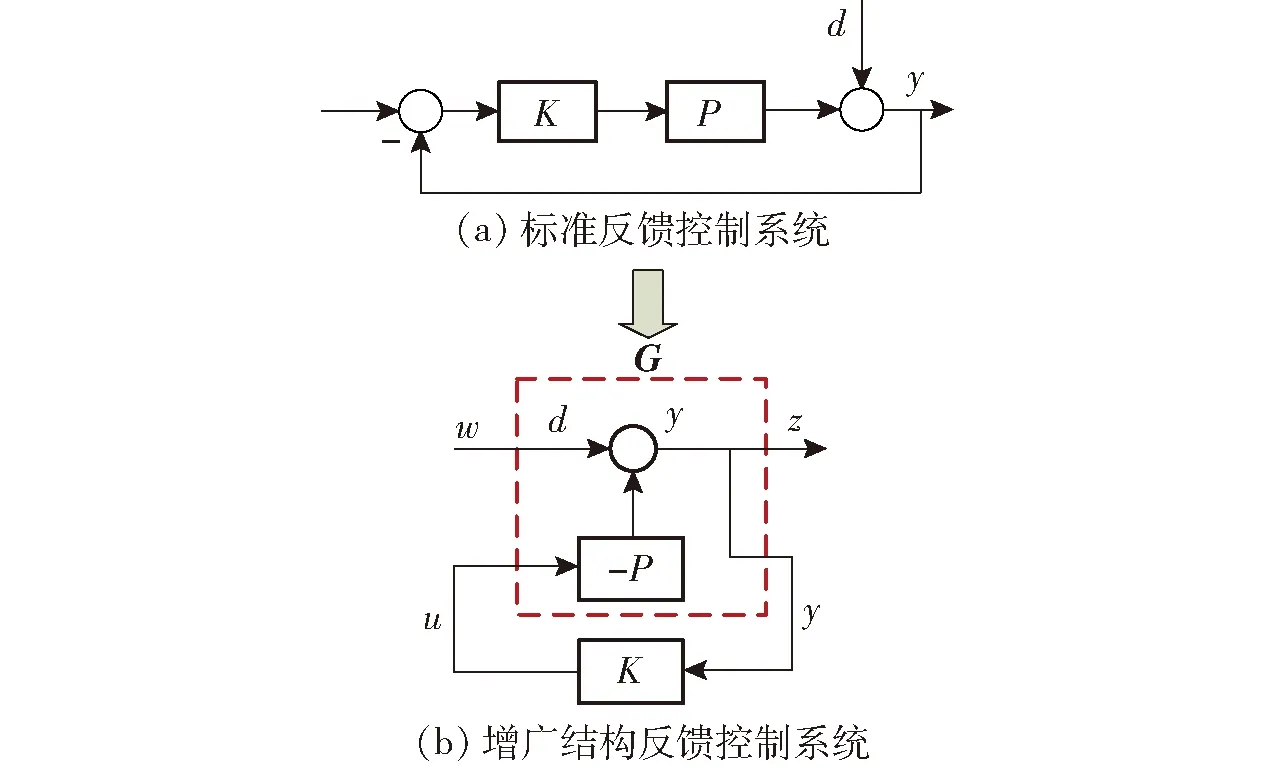
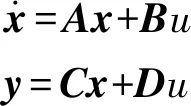
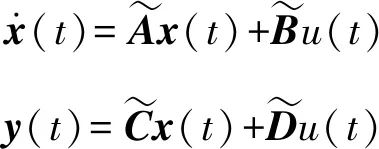
4 控制策略
4.1 仿真验证
4.2 试验分析
5 结束语

