射流离心泵动静叶栅匹配的水力与声学性能优化设计

郭 荣 李仁年,2 张人会,2

(1.兰州理工大学能源与动力工程学院， 兰州 730050； 2.甘肃省流体机械及系统重点实验室， 兰州 730050)

0 引言

叶轮与导叶均是影响射流离心泵水力性能和声学性能的重要过流部件[1-2]，同时，叶轮与导叶的动静干涉作用也是泵在运行过程中产生振动和噪声、影响泵运行稳定性的重要原因[3-5]。通过优化设计叶轮或导叶的几何参数来改善泵内部的流场分布特性进而提升泵的扬程和效率，一直是学者们研究的热点[6-11]。

近年来，统筹考虑叶轮与导叶的匹配关系、探索动静叶栅的最优结构组合、提升流体机械性能的研究，也越来越普遍[12-14]。张德胜等[15]分析了叶轮叶片数、导叶叶片数及其厚度对斜流泵内部压力脉动特性的影响，为斜流泵的设计和稳定运行提供了参考；汪家琼等[16]以提高多级离心泵的水力效率为目标，对叶轮和径向导叶不同组合、不同工况下的内外水力性能进行分析，发现叶轮和导叶内部的涡流是降低泵水力效率的主要因素；王文杰等[17]为分析叶轮与导叶匹配对余热排出泵水力性能的影响，设计了4种不同组合方案，发现叶轮与导叶的匹配对余热排出泵在小流量工况和大流量工况的性能影响较大，而对额定工况下的性能影响较小；杨从新等[18]基于核主泵几何参数，建立叶轮叶片数和导叶叶片数的多种匹配方案，通过数值方法预测了多种匹配方案下核主泵额定工况下的水力性能，为核主泵叶轮和导叶叶片数的选取提供了理论依据；王洪亮等[19]采用数值计算与试验相结合的方法，在叶轮与导叶叶片数组合变化下，对井用潜水泵的性能变化规律和内部流场分布进行了研究。

学者们对动、静叶栅的匹配与泵的水力性能之间的关系做了大量工作，但考虑的主要因素为叶轮叶片数与导叶叶片数，未涉及动静叶栅型线、动静叶栅间隙及其对声学响应特性的影响。本文围绕叶轮和正导叶相关结构参数，采用正交试验方法，结合CFD/CFA技术对射流离心泵的动静叶栅匹配进行多目标优化设计，以期为提升叶轮与导叶的水力设计水平、优化动静叶栅干涉对泵的水力性能及声学响应特性影响提供参考。

1 优化模型及试验设计方案

1.1 优化对象

以JET750G1型射流离心泵为优化对象，该泵结构如图1所示。其主要设计参数如下：设计流量Q=2.5 m3/h，设计扬程H=23 m，设计效率η=20%，转速n=2 850 r/min，轴频为47.5 Hz，叶频为285 Hz。叶轮叶片数Z1=6,叶轮进口直径Dj=40 mm，叶轮出口直径D2=120 mm，叶轮出口宽度b2=5.3 mm，叶片包角φ=76°；导叶基圆直径D3=125 mm，正导叶叶片数Z2=5，反导叶叶片数Z3=5；喷嘴进口直径d1=24 mm，喷嘴出口直径d2=9 mm。

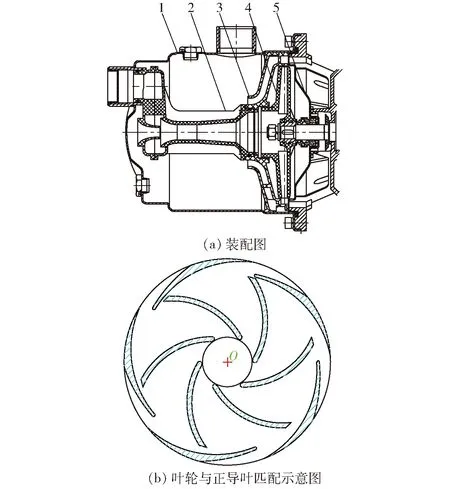
图1 模型泵结构图Fig.1 Structural diagrams of model pump1.泵体 2.喷射器 3.导叶 4.叶轮 5.泵盖

1.2 叶片型线的参数化

模型泵叶轮和导叶均为圆柱形叶片，该类型叶片采用Taylor多项展开式进行参数化控制，可通过改变多项式中的变量系数实现对叶片的快速高效变形。Taylor多项展开式控制叶片型线的原理如图2所示，图中R1为叶片进口直径，R2为叶片出口直径。

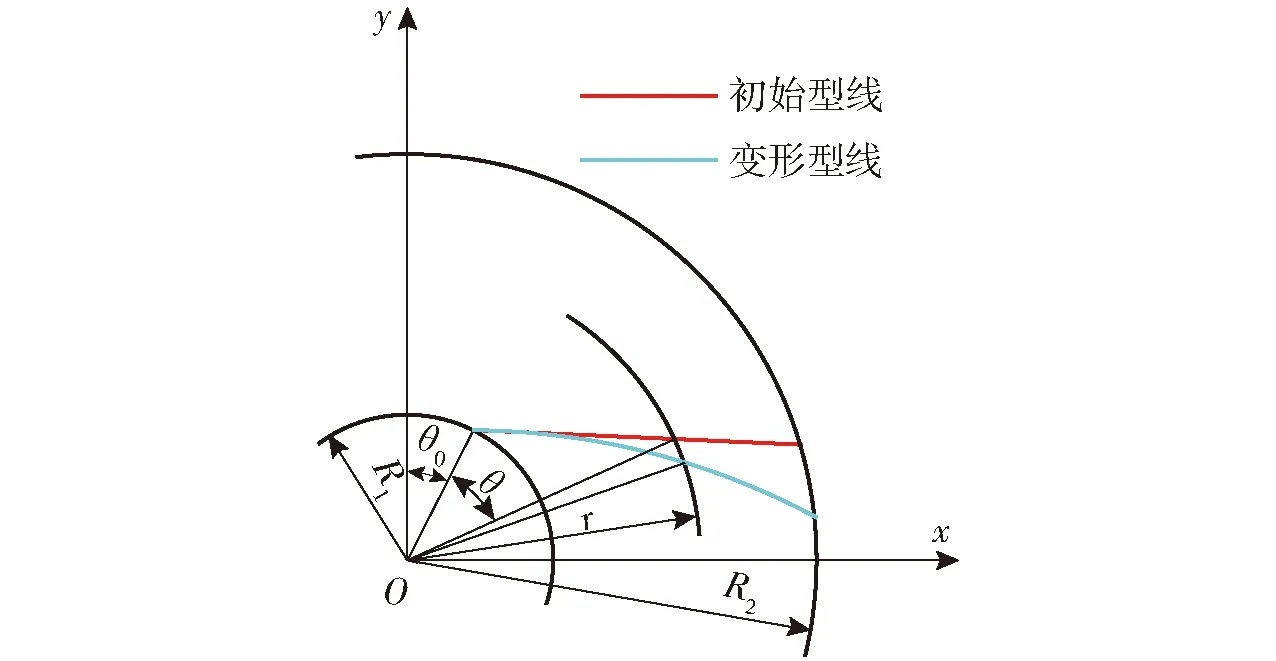
图2 Taylor多项展开式控制叶片型线原理图Fig.2 Schematic while blade profile controlled by Taylor polynomial

圆柱形叶片型线上的点可以表示为

f(r,θ)=0

(1)

由式(1)，任意叶型可以表示为最初叶片型线基础上的Taylor展开式，即

(2)

其中

r0=(R-R1)/(R2-R1)

式中θ0——初始圆柱角

θ——圆柱角

ai——控制变量

R——实际半径

r0——无因次半径

式(1)可以视为是未知函数θ(r)在θ0点的Taylor展开，这样，任意叶片型线都可以用式(2)表示。

模型泵叶轮为等厚度叶片，只需对叶片工作面进行参数化表示即可，导叶叶片厚度沿半径方向逐渐增加，需对工作面和背面分别进行参数化描述，分别为

θ1(r)=2.951 77r-5.098 06r2+7.140 66r3-
5.391 80r4+1.642 81r5

(3)

θ2(r)=6.283 19-1.914 79r+2.280 03r2-
3.422 35r3+2.723 91r4-0.858 29r5

(4)

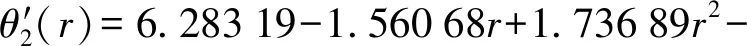
(5)

式中θ1(r)——叶轮工作面型线Taylor展开式

θ2(r)——正导叶工作面型线Taylor展开式

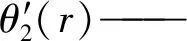
1.3 试验设计方案

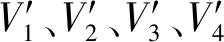
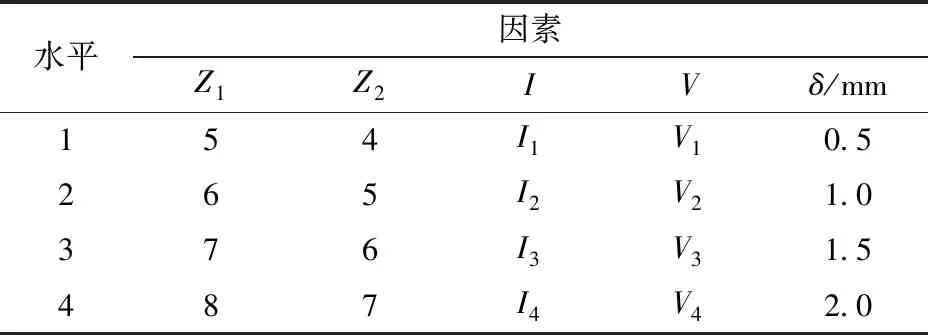
表1 因素水平Tab.1 Levels of orthogonal experimental factors

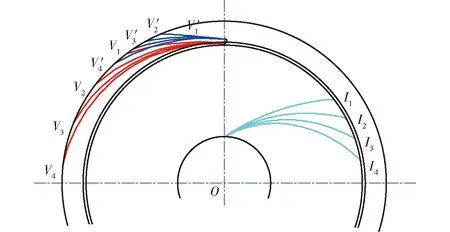
图3 不同因素水平的叶轮叶型和导叶叶型示意图Fig.3 Schematic of impeller profile and guide vane profile at different factor levels

选用L16(45) 标准正交表，结合因素水平表可得出16 种配置方案，如表2所示。通过数值计算可以得到不同动静叶栅匹配方案下泵的水力效率、扬程及叶轮诱导噪声、导叶诱导噪声。

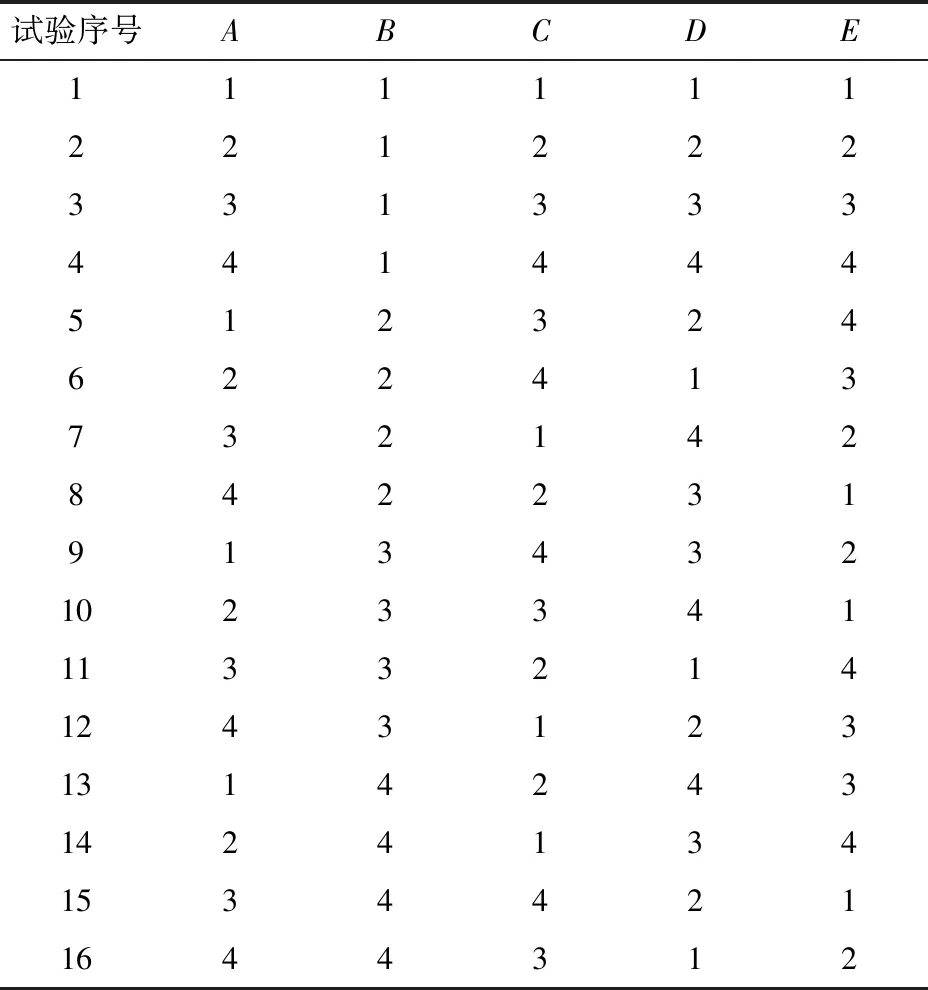
表2 正交试验方案Tab.2 Orthogonal experimental schemes

1.4 多目标优化方案的确定

本研究采用一种矩阵分析法确定多目标正交试验设计的优化方案，该方法克服了通过综合平衡法、综合评分法等方法确定多目标优化方案时运算量大、忽略指标间的差异和联系等缺点，通过计算得到各因素不同水平对试验结果考察指标影响的权重，判断因素对指标影响程度的主次顺序并快速得出全局优化方案[20]。

矩阵分析法需要根据数据结构建立一个包含n个因素，每个因素m个水平的3层数据结构模型，如表3所示。

表3中第1层为试验考察指标层，建立矩阵M，

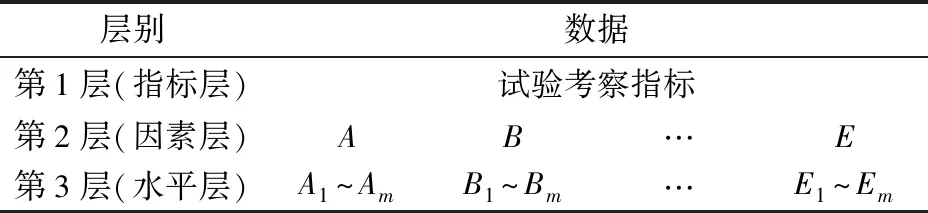
表3 多目标矩阵分析法数据结构Tab.3 Data structure of multi-objective matrix analysis

若因素i在j水平指标试验结果平均值为kij，如果考察的指标值越大越好，则令Kij=kij，如果考察指标值越小越好，则令Kij=1/kij；第2层为因素层，建立矩阵T；第3层为水平层，建立矩阵S，式中si为因素i的极差, 极差反映了因素对试验指标的影响程度，是将因素i求得的kij值中的最大值减去最小值。

(6)

(7)

其中

(8)

其中

最终得到试验指标值的权矩阵ω。由于Ki1Ti是因素i第1个水平的指标值占因素i所有水平的指标值总和的比，其与Si的乘积结果ωi反映了因素i的第1个水平对指标值的影响程度及其极差大小。

ω=[ω1ω2…ωn]T

(9)

2 数值计算方法

2.1 流场计算

整个计算域包括叶轮、导叶、喷射器、前泵腔、后泵腔、进水管、出水管及泵体，将重点研究部件叶轮与导叶计算域划分为六面体结构化网格，其他过流部件划分为四面体非结构化网格，网格划分通过ICEM CFD 16.0完成，经过无关性检查，确定网格总数约为3×106。模型泵叶轮与正导叶网格如图4所示。

图4 模型泵叶轮与正导叶网格效果图Fig.4 Grid diagram of impeller and positive guide vane of model pump

基于CFX 16.0软件进行流场计算。采用多重坐标系，叶轮流场在旋转坐标系中计算，其余部件流场在静止坐标系中。采用k-ω湍流模型，动静部件间使用GGI(General grid interface)交界面技术进行数据交换。设置压力进口、速度出口边界条件，进口压力依据试验测试得到的进口压力给定；所有固壁表面采用无滑移壁面条件，并按实际加工设置粗糙度为25 μm；湍流黏度项采用二阶迎风格式，时间项采用二阶全隐格式进行离散，计算精度为10-4。时间步长设置为0.000 117 s，即每个时间步长内叶轮转过约2°。先进行定常计算，将定常计算的结果作为初始场进行非定常计算，待流场呈现出稳定的周期性变化后，输出叶轮表面8个旋转周期压力脉动信息文件用于后续声场计算。

2.2 声场计算

采用声学有限元(FEM)方法求解导叶固定壁面偶极子声源及叶轮旋转壁面偶极子声源诱发的流体动力噪声，声场计算借助LMS Virtual.Lab软件完成。声学有限元网格单元长度计算公式为

(10)

式中L——网格单元长度，m

c——声音传播速度，m/s

fmax——最大计算频率,Hz

考虑模型的结构特点，给定单位网格步长为8 mm。分别求解导叶和叶轮诱发的噪声时，将其他过流部件表面设置为全反射壁面，即声音沿途传播没有透射，只沿着水传播至上下游；将泵的进、出口边界条件定义为全吸声属性。在泵的出口3倍管径处设置监测点。

在噪声测量中，采用1/3倍频程频谱分析能更准确地反映噪声源的频谱特性，便于较全面了解声源产生机理和提出降噪对策[21]，本研究使用最接近人耳主观感觉的A计权法对动静叶栅内流体动力噪声各频率的声压进行评价，并将评价后的1/3倍频程各中心频率声压级通过能量求和法进行叠加，获得总声压级。能量求和法公式为

(11)

式中LP——叠加后的总声压级

M——1/3倍频程的中心频率叠加数

Lpi——评价后的1/3倍频程各中心频率声压级

2.3 数值方法准确性验证

流场计算和声场计算的准确性验证，在甘肃省流体机械及系统重点实验室射流离心泵水力性能及流体动力噪声试验台完成，试验系统结构如图5a所示，叶轮和导叶的实物图如图5b所示。

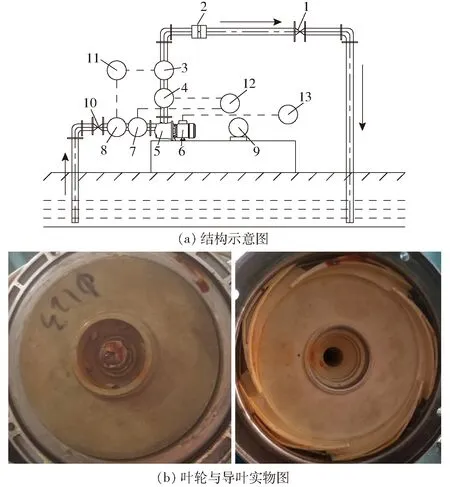
图5 试验系统Fig.5 Testing system1、10.阀门 2.流量计 3、8.压力传感器 4、7.水听器 5.模型泵 6.电机 9.转速仪 11.计算机 12.示波器 13.电测仪

表4为主要工况点模型泵水力性能试验及数值计算结果对比，其中水力效率在各主要工况点的计算值大于试验值，最大误差为4.6%；扬程的计算值在小流量点小于试验值，在额定流量及大流量点大于试验值，误差绝对值最大为3.2%；轴功率计算值整体小于试验值，随着流量增大，误差绝对值逐渐缩小，误差绝对值最大为7.9%，上述分析反映计算结果有较好的精度，计算方法可靠。

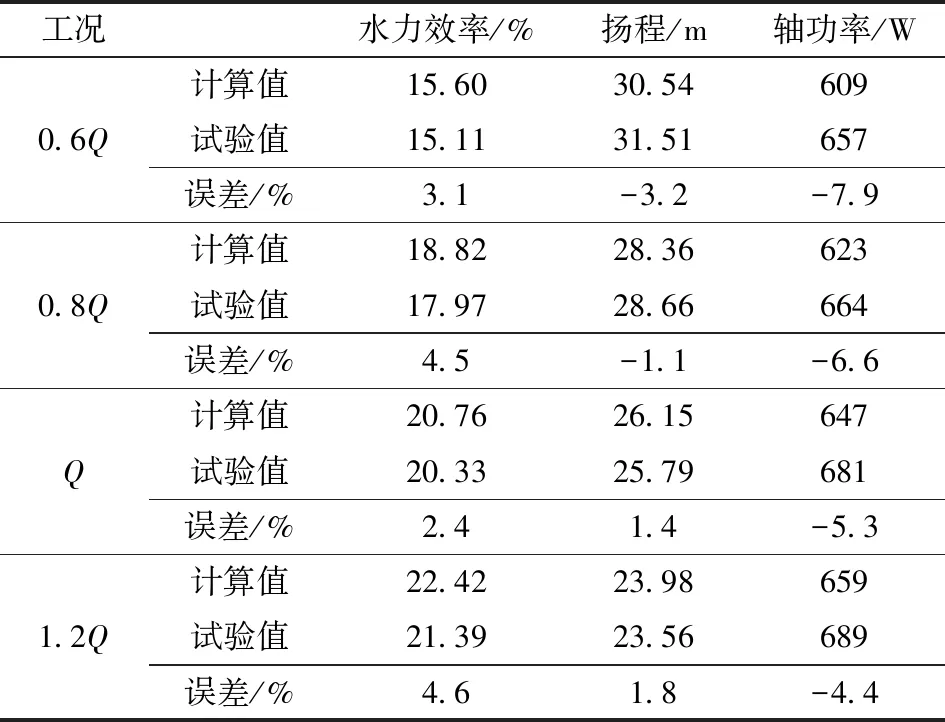
表4 主要工况点模型泵计算值与试验值对比Tab.4 Comparison between calculation and test of model pump at main operating points

图6为额定工况下监测点位置，模型泵流体动力噪声数值计算和试验测量频率响应曲线对比。其中导叶诱导噪声频响曲线以叶频(叶片通过频率，Blade passing frequency, BPF)为周期呈脉动现象，声压级幅值表现在叶频及其倍频处，因此导叶诱导噪声主要表现为BPF噪声。而叶轮诱导噪声频响曲线以轴频(47.5 Hz)为周期进行脉动；叶轮诱导噪声在各频段明显大于导叶，且其幅值与试验得到的噪声曲线较为吻合，是射流离心泵内场流体动力噪声的主要来源[2]。

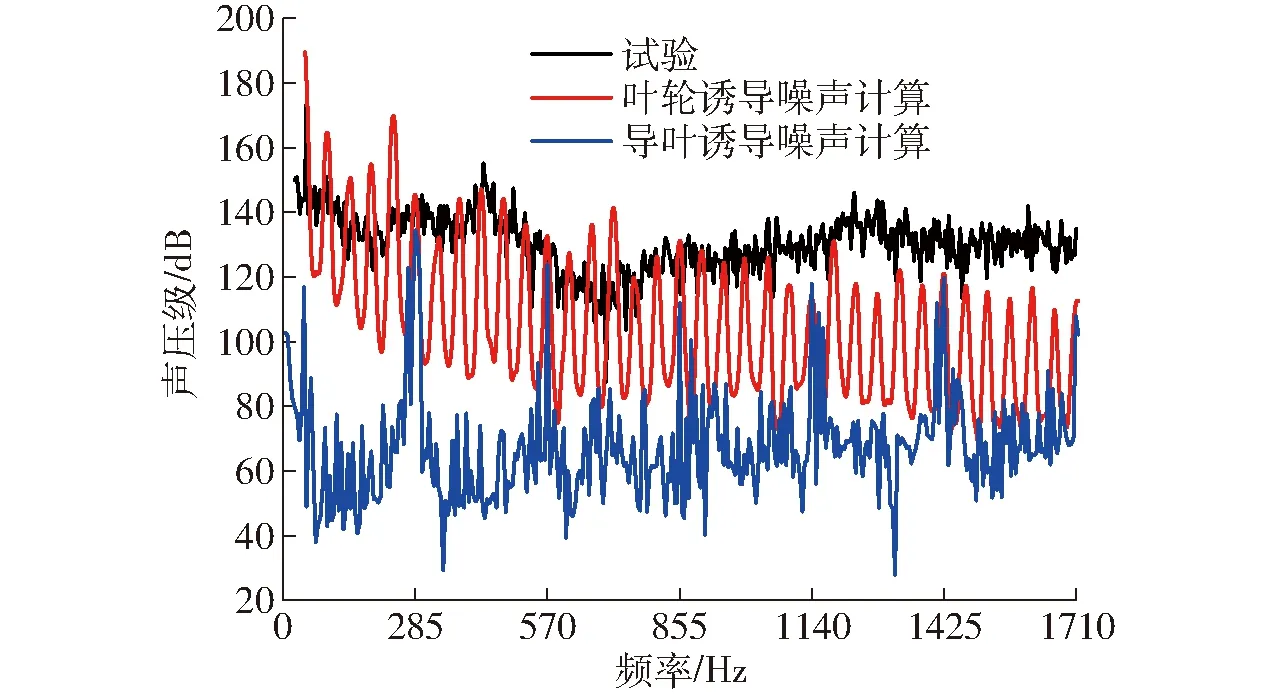
图6 声压级频响曲线计算与试验对比Fig.6 Comparison of sound pressure level frequency response curves between calculation and test

3 结果与分析

3.1 计算结果

保证模型泵其他过流部件结构不变，对表2的16种叶轮和正导叶结构配置方案在额定工况点处进行流场和声场数值计算，计算结果如表5所示。

3.2 直观分析

本研究优化目标包含水力性能和声学性能，其中水力性能包括扬程和水力效率2个指标，声学性能包括导叶诱导噪声和叶轮诱导噪声2个指标，因此属于多指标正交优化试验，为找出主要因素及优化方案，首先对试验结果进行直观分析。

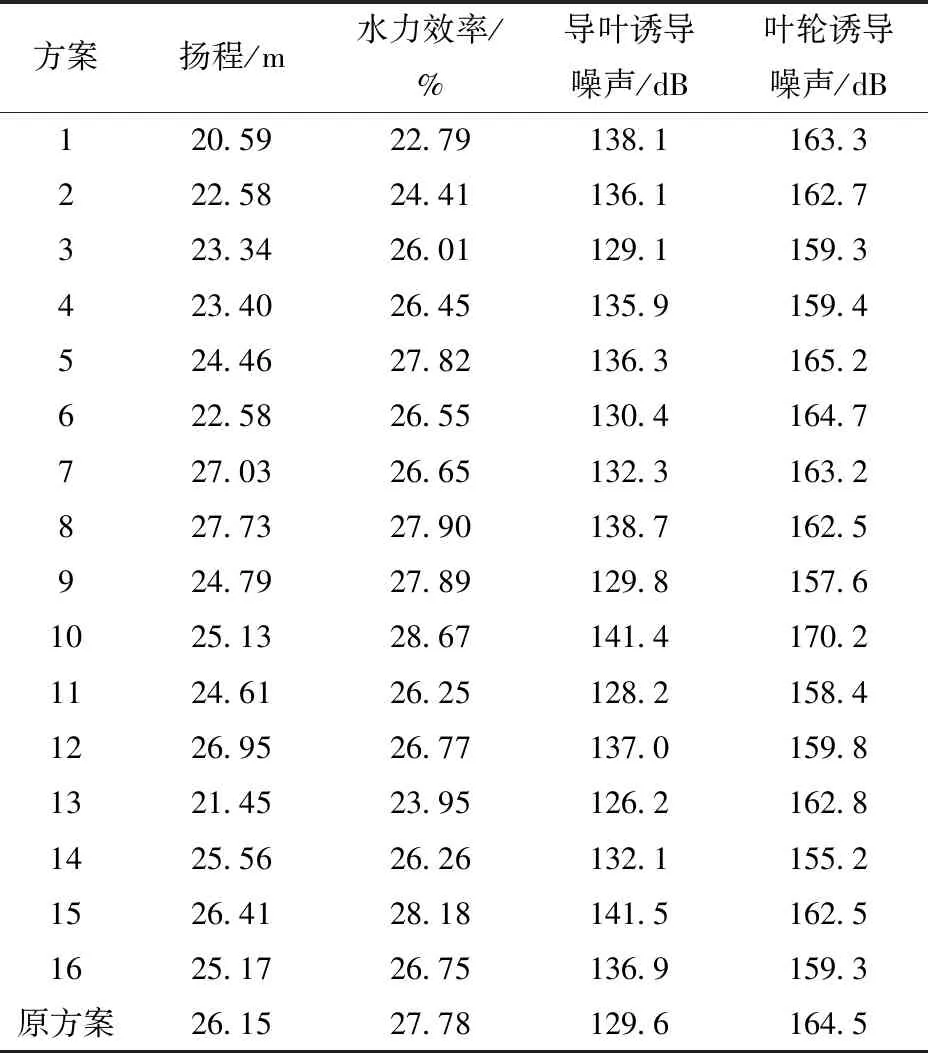
表5 试验方案数值计算结果Tab.5 Numerical results of test schemes

从表5可以看出，对于水力性能，方案8扬程最高，即A4B2C2D3E1；方案10、15水力效率高，但这两种方案导叶叶片数与叶轮叶片数相同，容易发生共振，影响泵运行的稳定性，属于不可取方案，因此选择方案8为水力效率相对最优选择，即A4B2C2D3E1。对于声学性能，方案13导叶诱导噪声声压级最低，即A1B4C2D4E3；方案14叶轮诱导噪声声压级最低，即A2B4C1D3E4。

3.3 极差分析

极差反映因素水平变化对指标影响程度，极差越大，说明该因素所选的水平对指标的影响越明显，因此，极差最大的那一列的因素，就是对指标影响最显著的因素，也就是最主要因素。对表5正交试验数值计算结果进行极差分析，结果如表6所示。

从表6可以看出各影响因子对单指标性能的影响。其中对扬程影响的主次顺序为A、B、D、E、C，水力效率影响的主次顺序为B、C、D、A、E，对导叶诱导噪声影响的主次顺序为E、A、D、B、C，对叶轮诱导噪声影响的主次顺序为E、B、D、C、A。可以发现动静叶栅间隙是影响叶轮和导叶诱导噪声的最关键因素，同时影响导叶诱导噪声的次要因素为叶轮叶片数，影响叶轮诱导噪声的次要因素为导叶叶片数，反映了叶轮和导叶的相互干涉对动静叶栅内部的流体动力噪声影响至关重要。

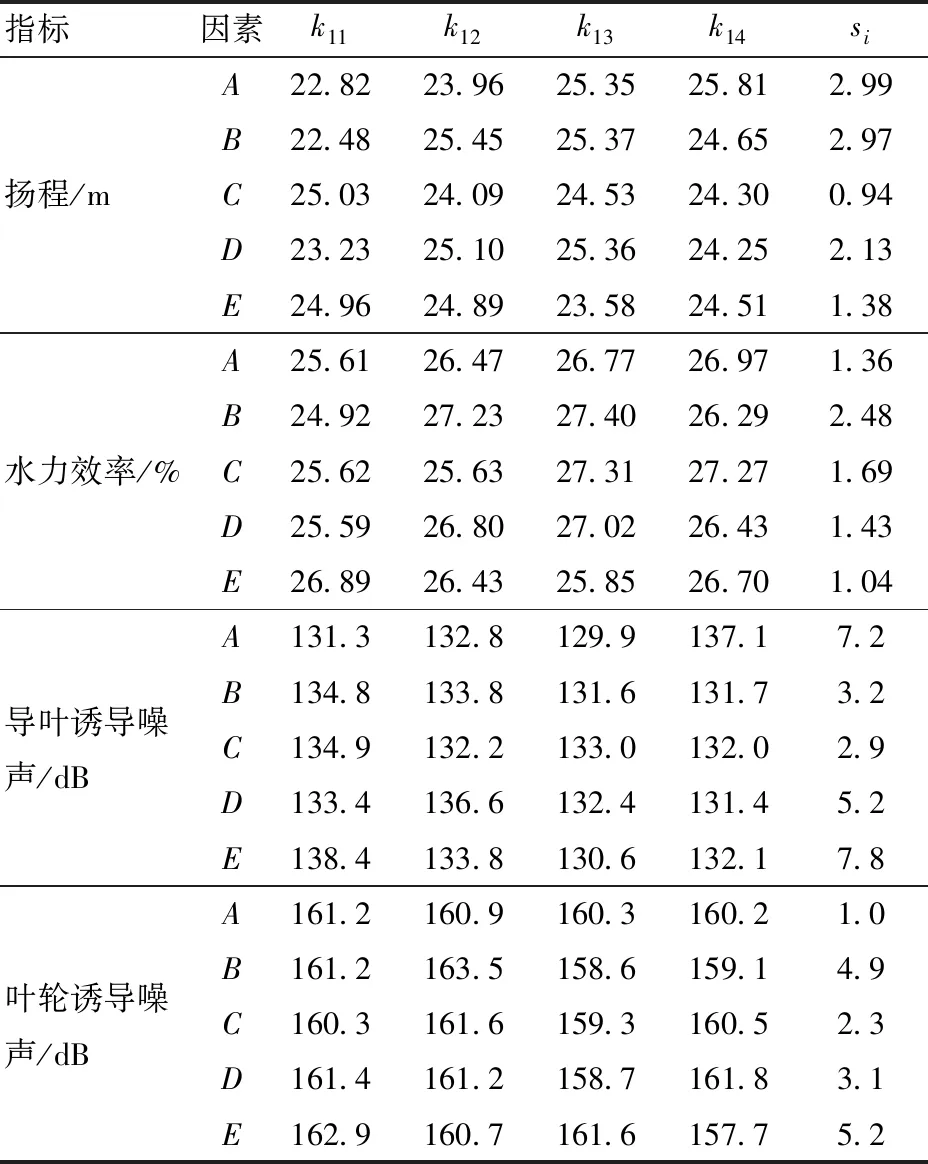
表6 极差分析结果Tab.6 Results of range analysis

对比影响各指标最显著的3个因素的极差值可以发现，动静叶栅的不同匹配方案对射流离心泵扬程的影响比对其水力效率的影响更加敏感，对导叶诱导噪声的影响比对叶轮诱导噪声的影响更加敏感。为直观显示不同因素水平对评判指标的影响程度，以因素水平为横坐标，各评判指标为纵坐标，得到如图7所示的因素效应曲线。

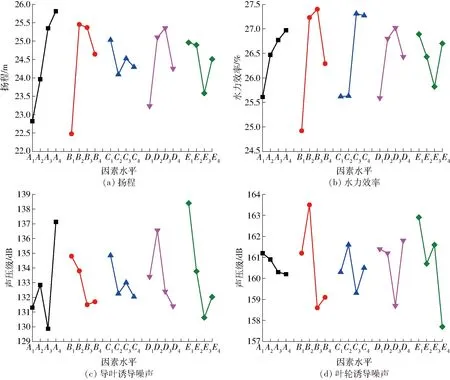
图7 优化指标效应曲线Fig.7 Effective curves of optimization indexes

对于水力性能，各优化指标越高则性能越优，由图7a、7b可以看出，叶轮叶片数A、导叶叶片数B、导叶型线D、动静叶栅间隙E4个控制因素对扬程和水力效率的影响规律一致，均随着叶轮叶片数的增多而单调递增，随导叶叶片数的增多、导叶叶片型线从V1过渡到V4而先增后减，随动静叶栅间隙的增大而先减后增。其中扬程的相对最优因素组合方案为A4B2C1D3E1,水力效率的相对最优因素组合方案为A4B3C3D3E1。

对于声学性能，各优化指标越小则性能越优，由图7c、7d可以看出，各控制因素对导叶诱导噪声和叶轮诱导噪声的影响规律并不一致，各因素的最优水平也不同。其中导叶诱导噪声的相对最优因素组合方案为A3B3C4D4E3，叶轮诱导噪声相对最优因素组合方案为A4B3C3D3E4。

3.4 综合性能优化方案

采用1.4节所述矩阵分析方法确定兼顾水力性能评价指标和声学性能评价指标的综合性能优化方案，分别计算出扬程、水力效率、导叶诱导噪声、叶轮诱导噪声4个考察指标的权矩阵。对于扬程和水力效率考察指标结果越大越好，此时对应的Kij=kij。而对于叶轮和导叶诱导噪声考察指标，则是越小越好，此时Kij=1/kij。代入式(6)～(9)计算可得每个考察指标对应的权矩阵，计算结果如表7所示,对表中4组考察指标权矩阵进行平均，得到综合性能最优的权重矩阵ωavg。

可以看出各因素对综合性能影响的主次顺序为B、E、A、D、C。其中因素B、C、D为3水平权重最大，因素A、E为4水平权重最大，因此可以快速确定综合性能最优方案为A4B3C3D3E4,即叶轮叶片数Z1=8,导叶叶片数为Z2=6，叶轮叶片型线为I3,导叶叶片型线为V3,动静叶栅间隙δ=2 mm。

4 优化结果验证和分析

4.1 外特性对比

将优化方案进行三维造型、网格划分及流场、声场的数值计算，并与原方案进行对比，验证采用矩阵分析法确定多指标优化方案的可行性和准确性。

优化后的水力性能和声学性能对比如图8所示。可以看出优化方案扬程相对于原方案在各主要工况点基本一致，水力效率在额定工况点附近略有改善；叶轮诱导噪声总声压级较原方案在各主要工况点均有明显下降，且流量越大降幅越明显，导叶诱导噪声总声压级在各工况点有小幅上升。

表7 权矩阵计算结果Tab.7 Calculation results of weight matrix

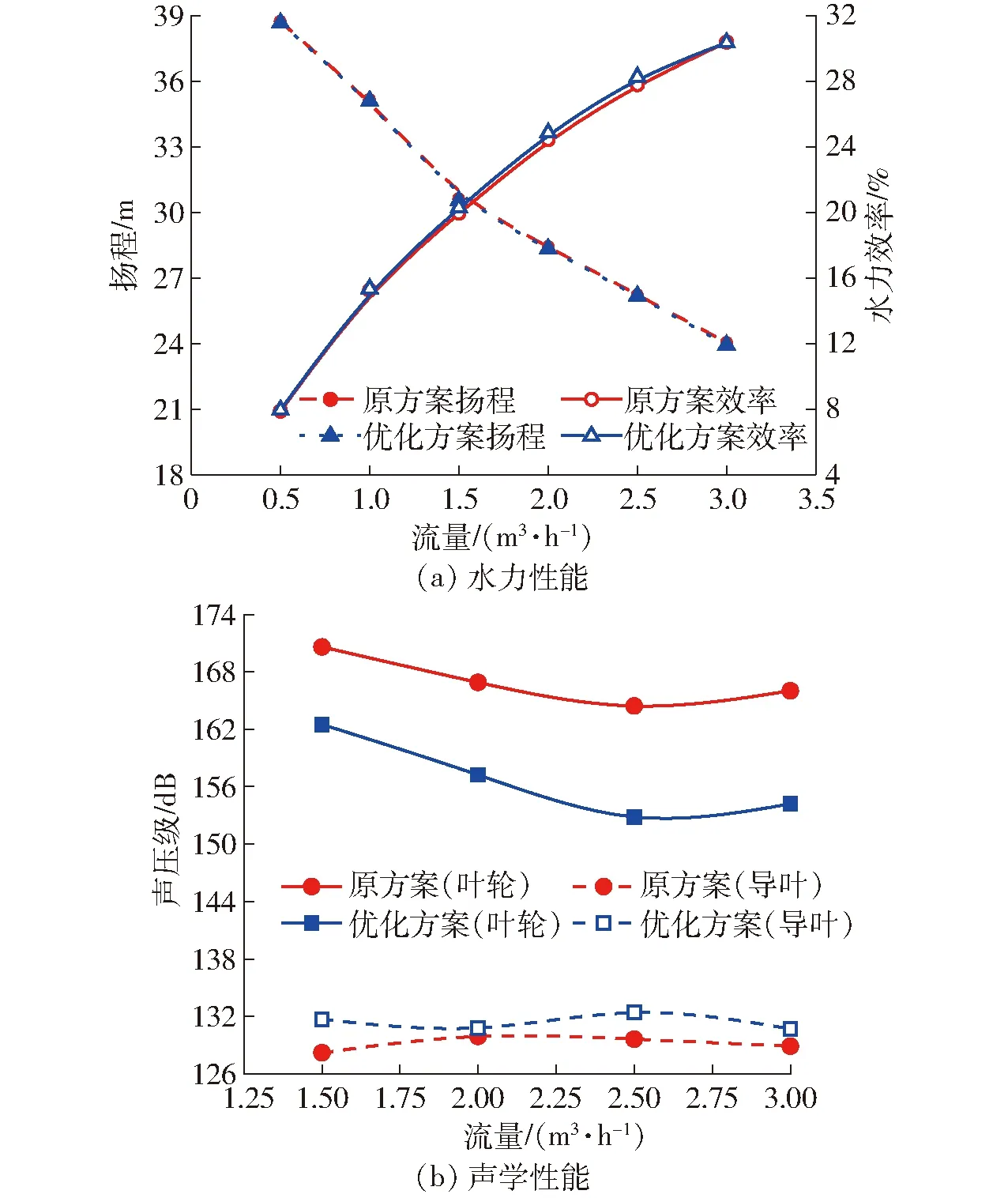
图8 优化方案与原方案性能对比曲线Fig.8 Comparison of performance curves between optimization and original models

对比额定工况点优化方案与原方案的数值计算结果，如表8所示。对于水力性能，优化方案较原方案扬程基本不变，水力效率提高0.5个百分点；对于声学性能，叶轮诱导噪声由164.5 dB降低为152.9 dB，降低7.1%，导叶诱导噪声由129.6 dB升至132.4 dB，提高2.2%。由于导叶诱导噪声水平低于叶轮诱导噪声超过15 dB，结合噪声叠加计算方法，可忽略导叶诱导噪声的影响，因此动静叶栅内的整体噪声得到明显改善。这表明采用矩阵分析法确定正交试验多指标优化方案是可行的。

表8 额定工况优化方案与原方案对比Tab.8 Comparison of optimization and original schemes results at rating

4.2 流场与声场分析

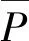
(12)

(13)

式中n′——网格节点序号

N′——一个叶轮旋转周期内压力采样数

t0——旋转周期的起始时刻

(14)

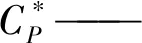
U2——叶轮出口处的圆周速度

ρ——密度

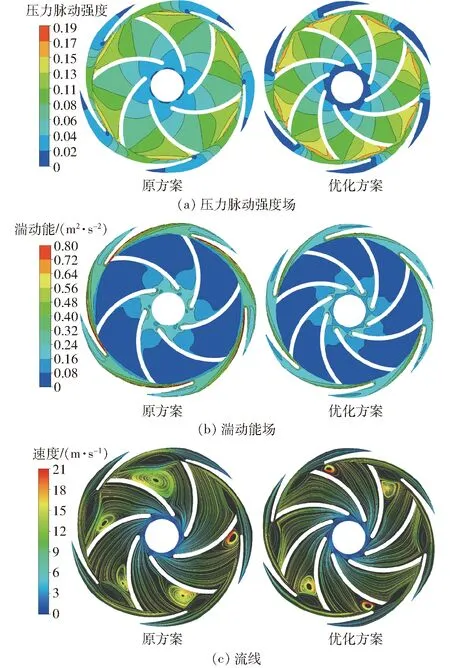
图9 优化前后动静叶栅内流场对比Fig.9 Comparisons of flow field in rotor and stator before and after optimization

图9为动静叶栅内中间平面处优化方案和原方案的压力脉动强度场、湍动能场及流线对比。由图9a可以看出，压力脉动强度在叶轮进口及导叶出口处最小，在叶轮内随着半径增大逐渐增大，在正导叶内随着半径增大逐渐减小，无论叶轮还是导叶，工作面强度大于背面，其中最大值出现在叶轮出口靠近工作面位置；优化方案压力脉动强度在叶轮进口和导叶出口低于原方案，但在靠近叶轮和导叶的交接面位置高于原方案，反映了优化后的叶轮和导叶内部流场变化梯度更大，上述分析结果表明压力脉动诱导的流体动力噪声不仅与压力在时间域的脉动强度有关，更与压力脉动强度在过流壁面的分布特性密切相关。由图9b可以看出，湍动能在导叶内部整体大于叶轮内部，其中导叶工作面及叶轮叶片入口处强度较大，优化方案动静叶栅内部的湍动能强度明显减弱。由图9c可以看出，优化方案叶轮内的漩涡数量有所减少，大小也明显减弱，动静叶栅交接处的流动排挤作用也有所改善。由图9b、9c分析结果表明，优化后的动静叶栅匹配方案改善了叶轮和导叶内部的流场结构，有利于减少流动损失，提高泵的水力效率。

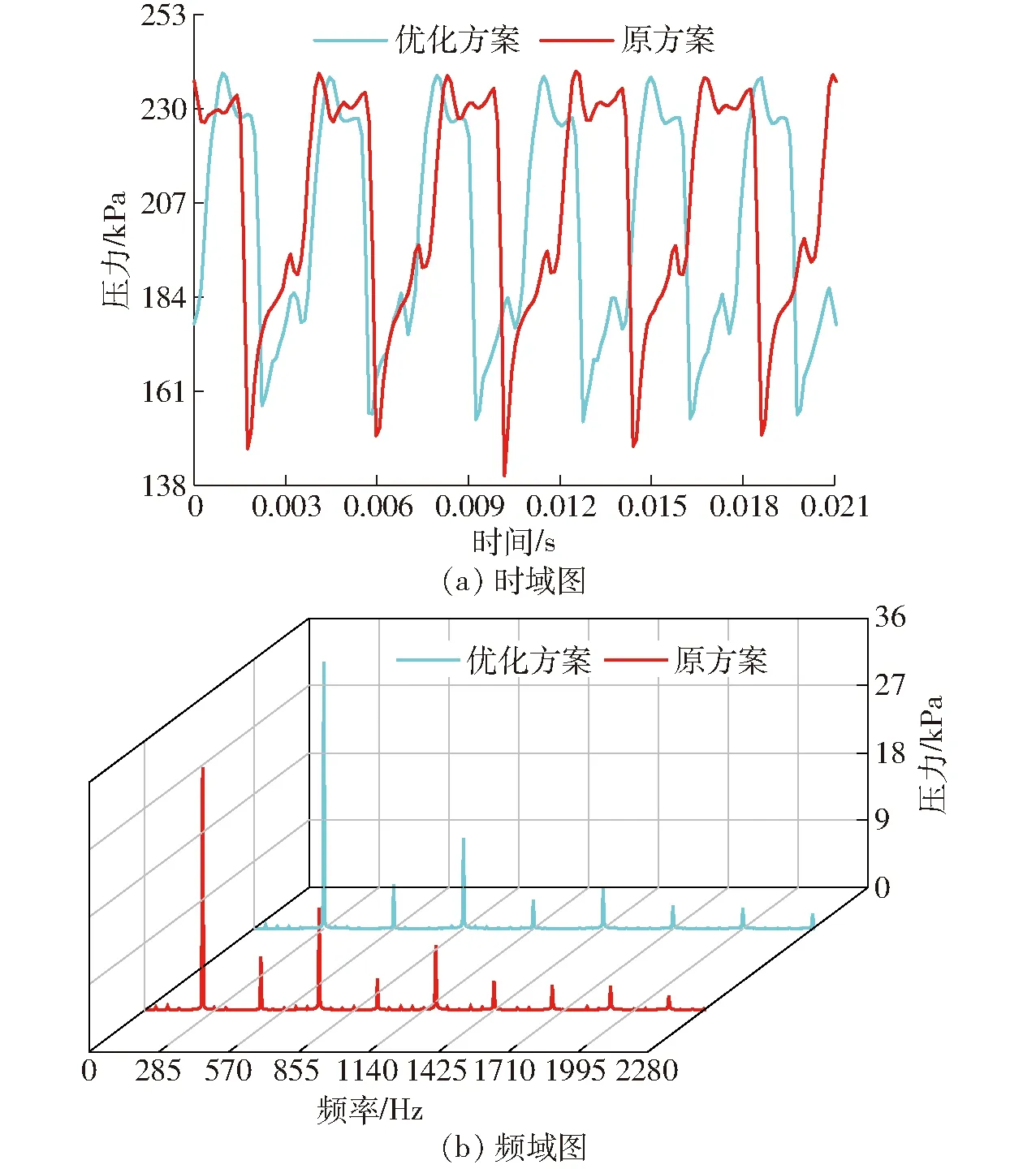
图10 优化前后叶轮出口监测点压力脉动时域和频域曲线对比Fig.10 Time and frequency domain comparison curves of pressure fluctuations at impeller outlet monitoring points before and after optimization

图10为叶轮出口监测点(监测点相对叶轮旋转坐标系静止)在一个叶轮旋转周期(约0.021 s)的压力脉动时域图及其频谱曲线。由图10a可以看出，压力脉动在叶轮旋转一周的时间内呈现相似波形的个数与导叶叶片数一致，即当叶轮叶片扫掠导叶叶片时，就会出现一个明显的波峰，优化后压力脉动的时域曲线脉动区间范围略有减小；由图10b可以看出，压力脉动的特征频率为导叶叶频(叶轮轴频乘以导叶叶片数)及其低阶倍频，其中主频均为导叶叶频，优化方案脉动幅值在主频处增大，在其他特征处升降各异。对比图6可知，叶轮诱导噪声的频谱特性与叶轮内部流场的压力脉动频谱特性有较明显的区别。

图11为导叶入口监测点在一个叶轮旋转周期的压力脉动时域图及其频谱曲线。由图11a可以看出，原方案监测点处压力脉动在叶轮旋转一周的时间内呈现6个相似波形，而优化方案则呈现8个相似波形，均表现出与叶轮叶片数一致的特征，优化后压力脉动的时域曲线整体略有下移；由图11b可以看出，两种方案压力脉动的特征频率均为叶轮叶频及其低阶倍频，其中原方案脉动主频为285 Hz，优化方案主频为380 Hz，该值为叶轮的轴频和叶轮叶片数的乘积。对比图6可知，导叶诱导噪声的频谱特性与其内部流场压力脉动频谱特性基本一致，特征频率均为导叶叶频及其低阶倍频。

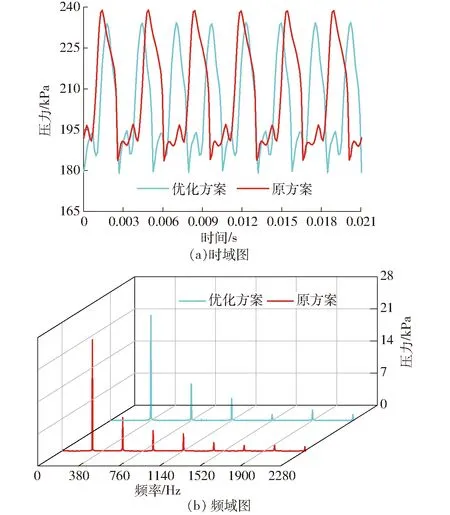
图11 优化前后导叶入口监测点压力脉动时域和频域曲线对比Fig.11 Time and frequency domain comparison curves of pressure fluctuations at vane inlet monitoring points before and after optimization

由图10、11可以发现，叶轮内部压力脉动的时域和频域特性曲线主要与泵的运行参数(转速)和导叶结构参数(叶片数)相关，而导叶内部的压力脉动时域和频域特性曲线主要与泵的运行参数(转速)和叶轮结构参数(叶片数)相关，反映了动静干涉作用对叶轮和导叶内部的非定常流动特性有重要影响。

5 结论

(1) 采用矩阵分析法确定兼顾水力性能评价指标和声学性能评价指标的综合性能优化方案。优化后，额定工况下泵的扬程不变，水力效率提高0.5个百分点，动静叶栅内的整体噪声得到明显改善，其中叶轮诱导噪声降低7.1%，导叶诱导噪声提高2.2%，验证了采用权矩阵分析法确定正交试验多指标优化方案的可行性。

(2) 动静干涉作用对串列叶栅内的流体动力噪声有重要影响，导叶诱导噪声主要影响因素为动静叶栅间隙、次要因素为叶轮叶片数，叶轮诱导噪声主要影响因素为动静叶栅间隙、次要因素为导叶叶片数，表明低噪声射流离心泵设计的关键是合理确定动静叶栅间隙及动静叶栅的叶片数。

(3) 动静叶栅的不同匹配方案对射流离心泵扬程的影响比对其水力效率的影响更加敏感，对导叶诱导噪声的影响比对叶轮诱导噪声的影响更加敏感。

(4) 压力脉动引起具有偶极子特性的流体动力噪声，导叶诱导噪声的频谱特性与其内部内流场压力脉动的频谱特性基本一致，但叶轮诱导噪声频谱特性与其内部压力脉动的频谱特性有较明显的区别。