复杂环境下农业机器人路径规划优化方法
殷建军 董文龙 梁利华 谢伟东 项祖丰
(浙江工业大学机械工程学院, 杭州 310023)
0 引言
路径规划是移动机器人研究的基础[1-2],是指在障碍环境下遵循特定的评价标准,寻找一条从起始点到目标点的无碰撞移动路径[3-4],利用路径规划算法进行不同方向优化也是移动机器人研究的热点问题[5-7]。
机器人工作工况与所处环境紧密相关,不同的环境下使用的工作策略也不尽相同。当移动机器人进行室外作业时,考虑到室外地形大都不平坦[8],机器人在复杂地形环境下通常会受到自身功率和能量限制,局部产生不稳定[9],降低作业效率与工作完成率。传统的路径规划算法通常以距离为成本生成最优路径,但是在机器人实际运动过程中,这种最优路径由于变化率相对较高,反而会造成机器人的能耗过大。对于复杂环境下作业的机器人,通过能耗限制策略寻找最优路径极为重要,因此也出现了许多针对能量优化的室外路径规划算法。文献[10]提出了一种物理模型,可计算出在各种外力作用下移动机器人的能量损耗,并考虑了重力效应、功率限制等不平坦路面必须解决的问题。文献[11]改进了能量成本模型,确定了垂直轴理想锥体表面摩擦和重力作用的近似最佳路径。文献[12]引入了地形面重量概念,捕获一些基于位置的地形参数,并提出了一种多项式时间近似算法,用于寻找最短的各向异性路径。文献[13]提出了一种将估计能耗加入总行驶能耗的迭代算法,应用于强干扰环境。文献[14]提出了一种基于约束-感知的启发式路径规划算法,使用锯齿形路径模式估计不平坦地形上的成本。文献[15-16]对一些传统的算法根据能耗模型估算进行优化。文献[17-18]对机器人轨迹控制优化,降低了能耗。
本文提出一种Energy Constraint A*算法,是一种改进启发式搜索路径规划算法,简称ECA*算法。与文献[8]添加比例因子的方法不同,本文算法将利用距离-能量损耗模型作为路径搜索启发代价,在给定约束条件下,使用最佳优先搜索策略寻找能量损耗最优路径。
1 路径规划的损耗问题
1.1 距离-能量损耗模型
为了计算移动机器人在行进过程中的能量损耗,构造了两点之间距离-能量损耗模型,通过迭代累计和一定的约束限制,即可计算出移动机器人在整条路径中的能耗。
已知x、y两点的坐标,则x点到y点的损耗量可以表示为
L(x,y)=(D(x,y),E(x,y))
(1)
式中D(x,y)——x、y两点间的距离函数
E(x,y)——x、y两点间的能量损耗函数
考虑机器人移动时所克服的重力与摩擦力的影响,D(x,y)的计算公式为[19]
(2)
式中d(x,y)——x、y两点间的实际距离函数,采用欧氏距离进行计算
α(x,y)——x、y两点间的仰角函数
αmax——两点之间仰角的最大临界值
E(x,y)的计算公式为[19]
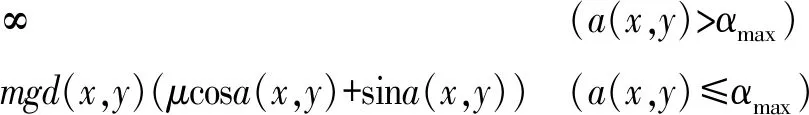
(3)
式中m——轮式机器人与机载质量
g——重力加速度
μ——机器人与地面间的动摩擦因数
在本文使用的算法中,两点的实际距离采用欧氏距离进行计算。
从式(2)、(3)中可以看出,当两点之间的角度超过最大临界值时,损耗量将变成无穷,所以为了减少能量的损耗,在搜索路径的过程中会把上升坡度变化率过高的路径剔除。
计算路径的损耗量时,假设在地图中存在一条可以从点ps到点pf的路径,则可将路径的总损耗量函数表示为
(4)
式中ηpspf——行进中所走过路径(点的集合)[20]
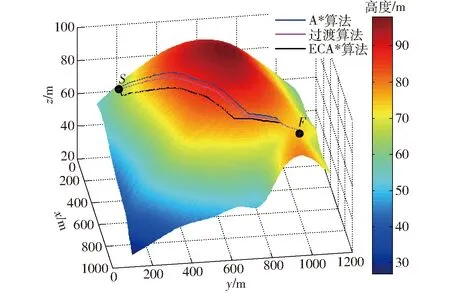
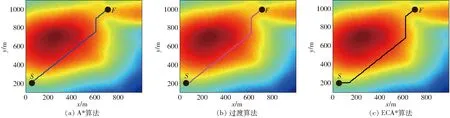
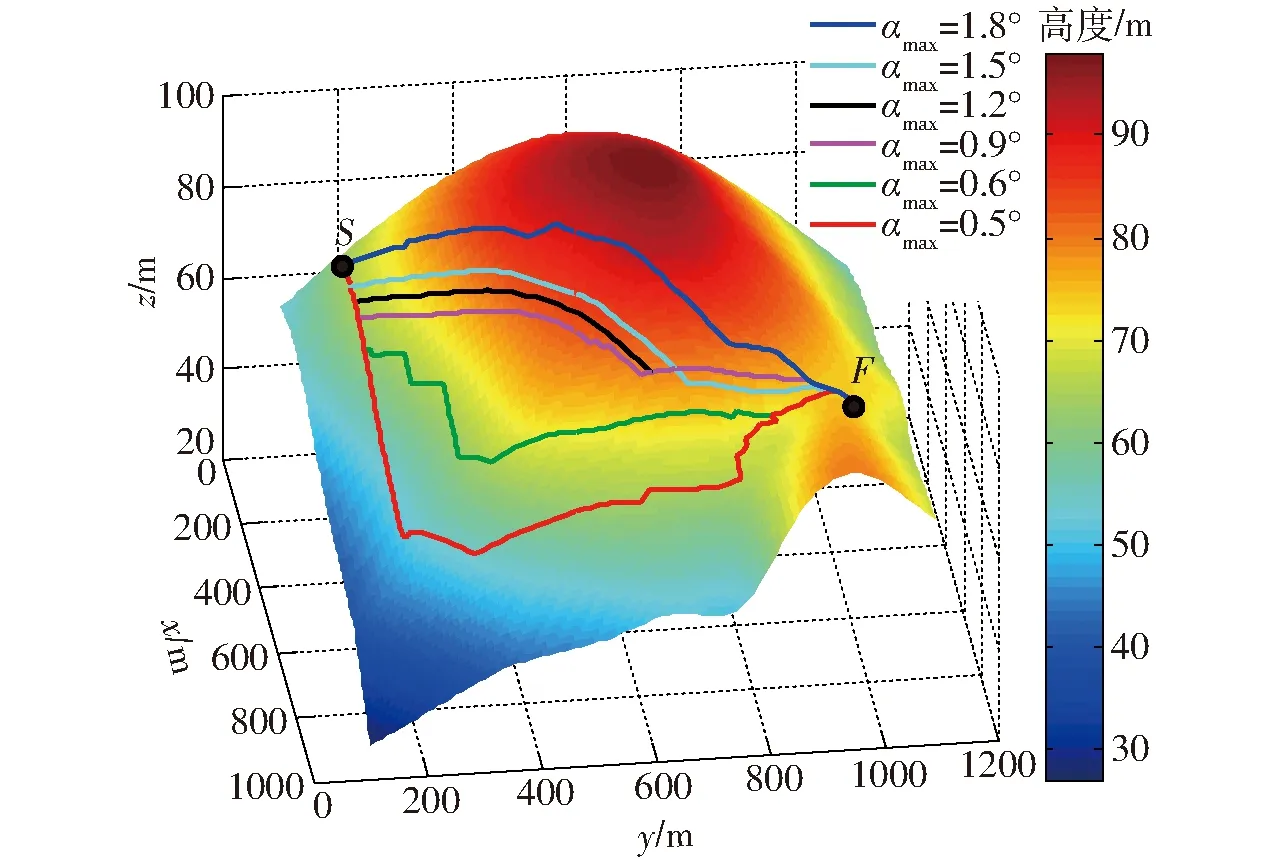
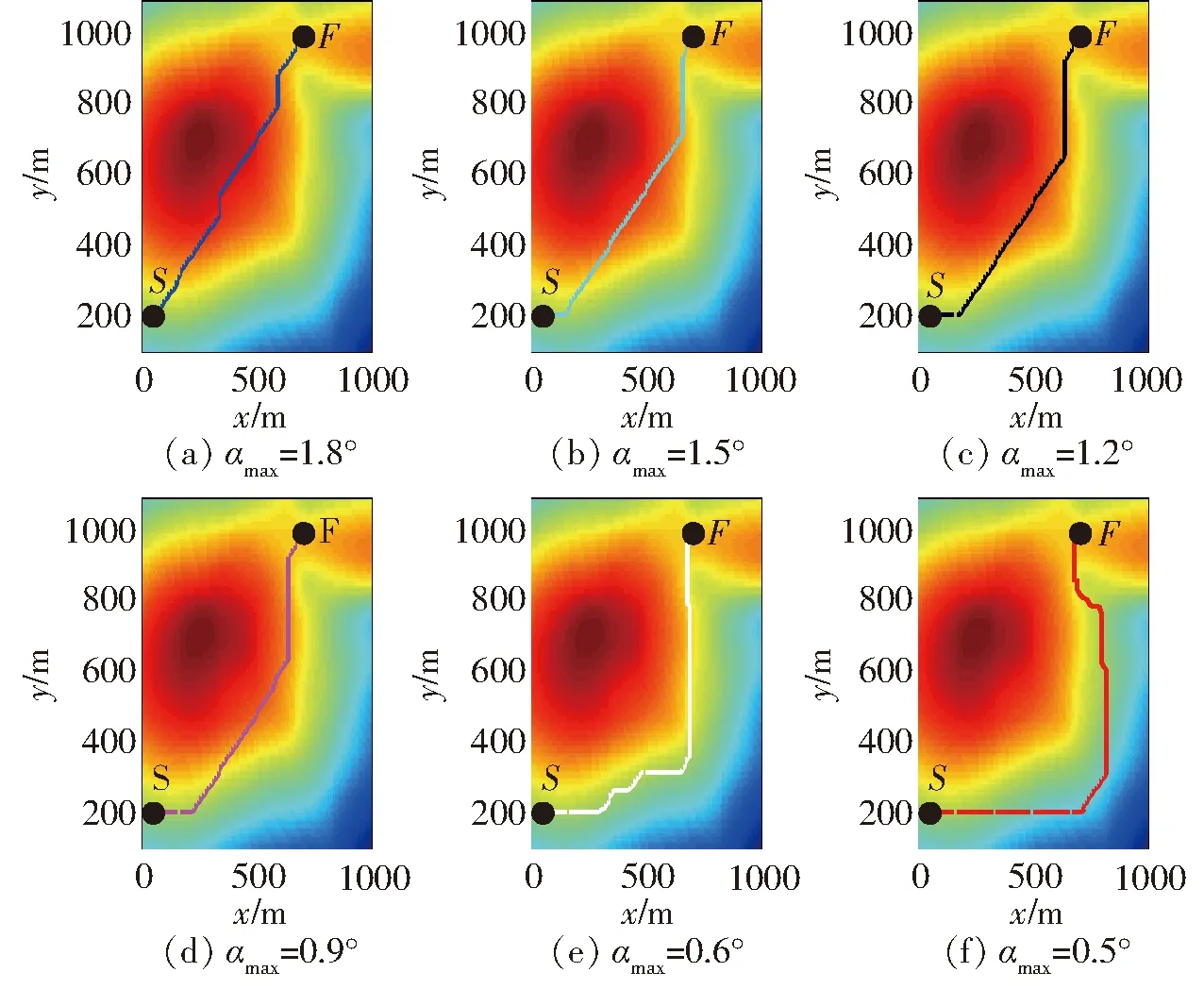
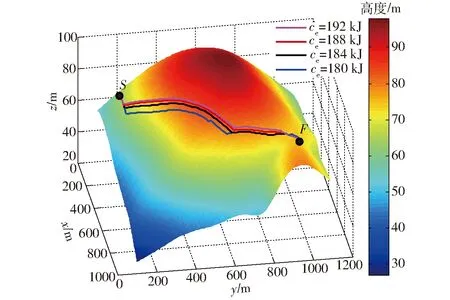
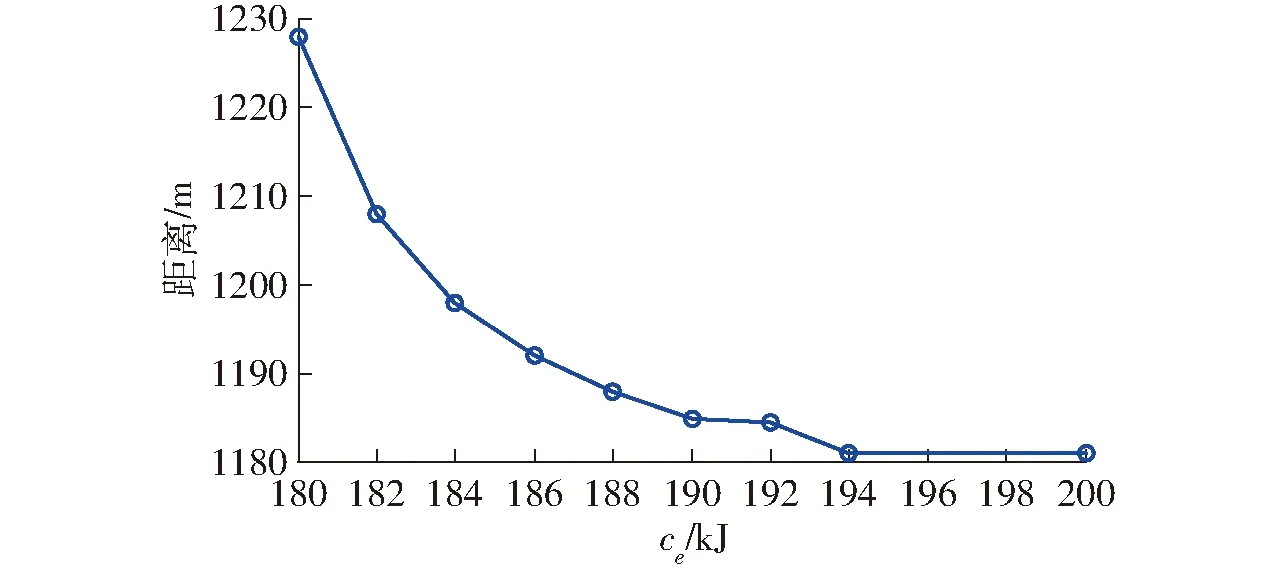
当s≤i (5) 式中pi——路径ηpspf所遍历的所有点 将式(4)代入到式(1)中,可得到 (6) 使用距离-能量损耗模型搜索路径时,距离的成本为行进时间,路径越长则耗费的时间越多,能量的成本为轮式机器人的电量。若只考虑距离的影响,则可能会造成电池能大量的浪费,若只考虑能量的损耗,则可能会大大增长完成路径的时间。所以在路径搜索过程中要兼顾两者。 在点ps到点pf的路径搜索过程中,定义距离-能耗约束为 C(ps,pf)=(cd,ce) (7) 式中cd——距离的约束值 ce——能量损耗约束值,为供电量最大值 假设算法搜索到路径ηpspf,路径损耗如式(4)所示,当且仅当 (8) 成立时,路径ηpspf得到保留,否则将此路径剔除。 传统的A*算法[21-22]是一种启发式搜索算法,具有最优性、完备性和高效性等优点[23]。A*算法的代价函数为 f(n)=g(n)+h(n) (9) 式中f(n)——当前节点总启发式代价 g(n)——起始点到当前点的实际代价 h(n)——当前点与目标点的估计代价 该算法的原理是从起始点开始,对周围的节点进行扩散,通过启发函数计算得到具有最小启发代价的点作为子节点,并将子节点移入到Close_list中,而其他已搜索到非最优的子节点则移至Open_list中,不断重复该过程直到搜索到目标点,最后通过回溯得到一条最优路径。 虽然传统A*算法能够高效地找出最短路径,但是并没有考虑到机器人实际的运动和消耗,最短路径同时也意味着机器人在行进过程中需要经历快速持续的地形变化以及大功率的输出,反而会造成更多的能量损耗。 假设要从地图上一点ps到达地图上的一点pf,已经搜索到的中间路径表示为ηn,引入距离-能量模型后,当s≤i F(ηn)=G(ηn)+H(pn,pf) (10) 其中 G(ηn)=L(ηn) (11) H(pn,pf)=L(pn,pf) (12) 式中F(ηn)——总的启发式损耗量 pn——当前节点 G(ηn)——走过中间路径ηn的损耗量 H(pn,pf)——当前节点到终点估计损耗量 ECA*算法的框架为 Initialize variables and lists insertε(ps) into Open_list while Open_list is not empty calculate the minε(pn) from Open_list if exist other entries select the best one remove the minε(pn) from Open_list insert the minε(pn) into Close_list ifε(pn) isε(pf) trace back and get the path else for eachε(pn+1) ofε(pn) calculateε(pn+1) ifε(pn+1) is out ofC(ps,pe) remove the path continue if existε′(pn+1) in Open_list or Close_list compare and choose the best one remove the paths continue insertε(pn+1) into Open_list 与传统A*算法类似,使用Open_list与Close_list记录地图节点的两种状态。Open_list记录搜索到但没有扩展的节点及路径, Close_list记录已经扩展了的节点及路径。每个节点pn通过数据结构ε(pn)记录4种不同的属性,分别为当前的节点pn、当前路径ηpn、G(ηpn)和F(ηpn)。 ECA*算法流程: (1)完成运算前的准备工作,初始化各个变量,并将初始节点放入Open_list中。 (2)在Open_list中计算选择最优节点,放入Close_list中。在选择过程中当路径和能量损耗处于矛盾时,优先选择路径最优。如果最优节点为目标点,则进行路径回溯获取最终路径。 (3)对最优节点进行扩展,对各个节点的属性值进行计算,扩展的同时剔除同一节点在Open_list和Close_list处于劣势的路径,并在列表中更新当前的最优路径。若在两个列表中都未记录节点,则将最新扩展的节点记录于Open_list列表中。 ECA*算法改进的地方在于以路径为主的思想,路径决定了行进的能耗,所以在列表中记录的不止有每个扩展点的属性,还记录了扩展点所在的路径和当前路径的损耗量。其中每一个扩展点有可能存在多个路径经过。当某一扩展点为当前计算的最优节点时,将同一个扩展点的路径进行对比,选择出距离最短、使用能量最少的路径进行再次扩展,将其他处于劣势的路径及时进行剔除,减少算法的计算量,提高了算法的计算效率。 针对路径规划的能耗问题,在三维栅格地图中运行路径规划算法并得到仿真结果。三维地形图选取学校周边高程图进行建模仿真,其中,地图采用WGS84坐标系进行构建,长半轴为6 378 137,扁率为298.26,采样地理位置为东经120.03°、北纬30.23°。为了降低计算量,地图的采样精度约为9.55 m(L15),仿真的三维地图如图1所示。两种算法均在Visual Stutio中实现,在仿真中算法采用的参数数值分别为:质量m为50 kg、重力加速度g为9.81 m/s2、摩擦因数μ为0.25、两点之间仰角的最大临界值αmax为0.15°。 图1 仿真中使用的三维地形图Fig.1 3D map of terrain used in simulation 在构造距离-能耗模型时,为了简化模型、提高算法计算的效率,并且考虑到路面属性的未知性,同时,控制变量摩擦因数一定,仿真的过程也将更加简便,结果也将更为直观,所以将模型中的滑动摩擦因数设定为常数,并忽略了机器人在行进过程中与地面的滑转率等相关的影响因素。因此仿真结果也将与真实值之间产生相对应的误差,但是与总的能量消耗相比,滑转率等因素产生的误差可以保持在一个较低的水平。而且控制不同的算法采用相同的能耗计算方式,也将体现出本文算法的有效性。 本次仿真过程中将使用3种算法进行路径规划,以展示ECA*算法的改进过程与结果。第1种算法为传统A*算法;第2种算法在A*算法的基础上设置相邻节点的仰角临界值,即αmax,若仰角超过临界值则表示两点间路径损耗超过预设值,则对路径进行剔除,是传统A*算法与ECA*算法的一种过渡算法;第3种算法即为ECA*算法。 将点S(50,200,65.04)m作为路径的起点,将点F(900,1 000,75.35)m作为路径的终点,爬升的高度为10 m。为了能够更清晰地观察路径变化,以下将分别在三维栅格图和平面云图中展示规划的路径,如图2、3所示,完成路径所需要行进的路程和消耗的能量对比如表1所示。 图2 不同算法的路径在三维栅格图中的对比Fig.2 Path comparison in grids with different algorithms 图3 不同算法平面云图中的路径对比Fig.3 Path comparison in cloud map with different algorithms 表1 不同算法完成的能量损耗对比Tab.1 Path energy loss comparison with different algorithms 能量损耗主要由行进过程中与路面的滑动摩擦和爬升高度决定。由图2、3可以看出,通过预设αmax的过渡算法能够避免行进至坡度过大的路径,进而避免由于不停爬升和下坡导致的能量浪费,所以优先选择较为平整的路面进行计算和规划。ECA*算法对过渡算法进一步改进,通过节点的扩展与路径损耗量的积累与启发计算,得到局部能耗最少的点组成的路径。ECA*算法在路程能量消耗上比传统A*算法的能量损耗减少14.87%,而实际增加的行程却可以忽略不计。仿真结果表明,ECA*算法通过一些局部路径的优化使得在路径少量增加的同时,能量损耗却大幅度降低。 在ECA*算法中,αmax的实际意义是移动机器人的最大爬坡角,代表了机器人的最大驱动能力。但在实际规划中,αmax不宜过大,通常可以减小αmax的值,以增大部分路程为代价(由上文可知此代价通常可以忽略不计),进而选更优的路径,但是同时αmax不能取值过小,否则无法得到真实的最优路径,图4、5为αmax对能量损耗的影响,表2为不同αmax完成路径的能量损耗。因此在机器人工作时需要根据实际工况,选择一个合适的αmax进行计算。 图4 不同αmax的路径在三维栅格图中的对比Fig.4 Path comparison in grids with different αmax 图5 不同αmax的路径在平面云图中的对比Fig.5 Path comparison in cloud map with different αmax αmax/(°)路程/m能量损耗/J1.811792468161.511811924941.211971815990.912161823130.614162112960.51689230209 上述仿真实验都是建立在没有损耗约束的情况下完成的,即C(ps,pf)=(∞,∞),而在移动机器人实际室外作业中,其能量总量通常是受限制的,因此在设定能量约束后,即C(ps,pf)=(∞,ce),不同ce对应的路径如图6、7所示。 图6 不同约束下三维栅格图的路径对比Fig.6 Path comparison in grids with different ce 图7 不同约束下生成的路径对比Fig.7 Path comparison with different ce 在没有约束的情况下,算法在执行从Open_list选择最优子节点这一步骤时,以距离最短作为选择条件;当在有约束的条件下,算法则可以选择出路径更长但能耗更少的路径,得到进一步优化。从仿真可以看出,ECA*算法可以通过增大行进路程为代价进而寻找到能耗较低的路径。 针对在室外复杂环境下作业的移动机器人存在因能量受限而降低工作完成率的问题,提出了一种基于改进的启发式搜索的ECA*路径规划算法,建立了一种距离-能量模型,并将模型与启发式搜索函数相融合,提出了新的代价函数,通过迭代、扩展、选择最优或次优子节点,剔除处于劣势的路径,进而寻找到能量损耗最优路径。仿真实验结果表明,相比于传统的A*算法,优化改进的路径可在仿真环境下节省14.87%的能量消耗,而且通过分析参数αmax的作用,添加相应的能量约束,ECA*算法可以得到不同的符合需求的路径,验证了其有效性。1.2 距离-能耗约束
2 算法改进
2.1 传统A*算法
2.2 改进算法
3 仿真实验
3.1 环境建模
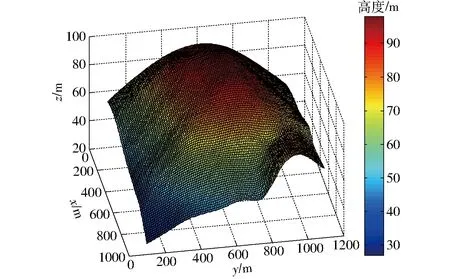
3.2 简化因素
3.3 不同算法的能耗对比

3.4 αmax对ECA*算法的影响

3.5 添加能量约束后的ECA*算法
4 结束语

