基于随机场理论的水电工程渣料场边坡稳定性分析

于晓天，曾亚武

(武汉大学土木建筑工程学院，武汉 430072)

0 引 言

随着西部大开发的持续推进，近年来我国在西部山区兴建了大量的水利水电工程。在这些水利水电工程的建设过程中不可避免地需要对原地貌进行相应的改造，从而产生大量的渣料，堆积后便形成渣料场。渣料场作为特殊的人工堆积边坡，其均匀性和稳定性受到堆填历史、堆填方式、降雨、工程扰动等诸多因素的影响，一旦失稳不仅有可能造成严重的生命财产损失，而且有可能造成严重的生态环境灾难。在开展渣料场边坡稳定性分析时，渣体抗剪强度参数的获取比较困难，一方面通过试验或经验取值都难以准确反映渣体的真实状态，即存在参数测不准的问题；另一方面，即使针对具体的渣体测得准确的抗剪强度参数，也只能代表测试试样的结果，不能代表整个堆渣体的抗剪强度参数，即堆渣体的抗剪强度参数存在空间变异性的问题。对于前者，大多数的研究以可靠度分析来考虑抗剪强度参数的变异性，属于随机变量模型范畴，但其前提是假定研究范围内抗剪强度参数是均匀分布的；而后者考虑的是空间不同点处局部与整体岩土物理力学性质之间的差异性，属于随机场理论的范畴。显然采用随机场理论来研究渣料场抗剪强度参数的空间变异性对其稳定性的影响，更加符合渣料场的工程实际，具有重要的工程意义。

目前，国内外学者利用随机场理论对非均质边坡稳定性问题进行了诸多有益的探究。如闫澍旺等[1]利用天津港现场的勘察资料首先建立了随机场模型，再利用方差折减技术分析了边坡的稳定性。祁小辉等[2]利用谱表现法建立随机场模型，并采用非侵入式有限元分析方法，分析了边坡可靠度。在国外，Griffiths和Fenton[3]基于随机场理论和有限元强度折减法提出了边坡可靠度分析的随机有限元方法。Low[4]利用FORM方法研究了抗剪强度参数的二维各向异性空间变异性对挪威南部黏土边坡失效概率的影响。Cho[5]利用Karhunen-Loeve(简称K-L)级数展开方法模拟土体参数空间变异性和MCS方法计算边坡失效概率。

显然，上述研究成果大多是围绕自然形成的非均质边坡稳定性进行的研究，相较于自然岩土体，渣料存在松散性明显、抗剪强度较低、降雨易入渗等特点。本文将针对水电工程渣料场这一特殊的人工边坡的稳定性问题，利用随机场理论，采用乔列斯基分解技术和非侵入式随机有限元法，研究渣料场抗剪强度参数的空间变异性对其稳定性的影响，为渣料场防护设计提供参考。

1 渣料参数空间变异性的模拟

1.1 自相关函数

在采用随机场理论分析岩土体参数空间变异性时，常用自相关函数表征岩土体中任意两点参数的自相关性，构建相应的随机场。

由于实际工程中得到的实际测量数据往往十分有限，我们假设随机场遵循平稳性假设，并且利用理论自相关函数来说明其空间相关性。蒋水华等[6]对5种理论自相关函数对边坡稳定性可靠度的影响做出了详细的说明，认为自相关函数类型对边坡稳定性研究的影响不大。本文采用形式最为简单，应用最为广泛的指数型自相关函数来表征渣料场抗剪强度参数在空间任意两点的相关性，其计算公式为：

(1)

式中：lx和ly分别为水平和垂直方向的相关距离，用于表征参数空间变异性的相关程度，相关距离越大，表示参数的空间相关性越强。

1.2 改进的乔列斯基分解法

采用随机场理论模拟岩土体参数空间变异性时，最关键的一步是将随机场离散为一组随机变量。

乔列斯基分解是近些年发展起来的一种离散随机场的有效方法[7]。相比较而言，利用乔列斯基分解技术离散相关非高斯随机场，计算过程简单、编程容易实现，且离散得到的随机变量数量等于随机场有限单元数量，物理意义直观[8]。然而，乔列斯基分解技术只能对单参数随机场进行离散，为此李典庆等[9]提出了改进乔列斯基分解技术用于相关多参数非高斯随机场的离散，取得了一系列成果，下面简单介绍改进乔列斯基分解技术的相关非高斯随机场的模拟步骤。

(1)划分随机场有限单元，得出每个随机单元中心点的坐标Qi=(xi,yi)，i=1, 2, …，n,n为随机场有限单元的数目。

(2)拉丁超立方抽样技术具有较好的一维投影和均匀分层分布的特性，样本能均匀地覆盖到变量概率分布的尾部，因此利用拉丁超立方抽样配点法随机产生一组每列含n个随机样本维度的独立标准正态空间随机样本向量ζ。

(2)

式中：θ为随机场的波动范围。

最后利用概率变换可以得到相关非高斯随机场。

由上述内容可知，相关非高斯随机场特征值的每个分量不仅取决于参数的自相关函数、波动范围、互相关系数，而且与有限单元的中心点坐标一一对应。

2 非侵入式随机有限元法

非侵入式随机有限元分析的最大特点在于确定性分析以及随机分析过程相互独立。确定性分析直接由现有的有限元计算软件执行，无需修改软件有限元源代码，直接建立边坡可靠度分析与通用有限元软件的接口，使得计算效率大大提高，能更快、更好地揭示岩土体参数空间变异性对渣料场稳定性影响的规律。本文以Geo-studio软件为例说明其主要的操作步骤如下：

(1)以渣料场抗剪强度参数均值在Geo-SIGMA/W模块中建立渣料场有限元分析模型，划分有限元网格，设置边界条件，在SLOPE/W模块中建立稳定性分析模型，并将SIGMA/W模块设为SLOPE/W的母模块。将边坡稳定性有限元分析模型另存为扩展名为xml的计算源文件，并提取出有限单元中心点的坐标。

(2)利用拉丁超立方抽样技术在独立标准正态空间中进行一次抽样，并利用改进乔列斯基分解方法模拟参数随机场，得到随机场样本值的一次实现。将样本值分别代替xml文件中相应的单元中心点上的参数均值，得到一个新的边坡稳定性分析文件。

(3)利用批处理软件直接调用Geo-studio软件，对新生成的xml文件进行稳定性分析。

(4)计算完成后会在当前文件夹中自动生成一个相应的计算结果文件，从中可以提取出相应的临界安全系数以及滑动面等信息。

(5)重复步骤(2)～(4)n次，计算得到相应的n个临界安全系数，以及相应的滑动面等信息。

计算流程如图1所示。

图1 计算流程图Fig.1 Flow diagram of calculatation

3 算 例

3.1 基本情况

为验算本文方法的可行性和正确性，本文以文献[6]中土质边坡为算例进行分析。边坡坡高H为10 m，坡度为1∶1，对应的土体抗剪强度参数及其空间变异系数如表1所示，抗剪强度参数符合对数正态分布，自相关函数采用指数型自相关函数。采用边长为0.5 m的四边形四节点二维实体结构等参单元，在坡面附近过度为三角形单元，将边坡剖分为1 210个有限元单元，如图2所示。采用理想弹塑性本构模型和摩尔库伦屈服准则，利用Geo-slope中“进入和退出”的滑移面选择方法计算该边坡的临界安全系数。

表1 边坡土体统计参数取值表Tab.1 Statistical properties of soil parameters

图2 算例边坡有限单元剖分示意图Fig.2 FEM model of slope

3.2 随机场实现

波动范围是表征岩土体参数空间自相关性的重要组成部分。显而易见，空间任意两处岩土体特性参数之间存在一定的差异性又存在一定的相关性，土体参数自身之间的这种自相关性一般随着两点间距离的增大而逐步减少，当距离大于某一定值后，自相关性可忽略不计，我们将这一定值称为波动范围。根据Vanmarcke[10]，波动范围的计算公式为：

(3)

式中：ρ(τ)为自相关函数；τ为空间任意两点间的相对距离；L为随机场区域计算尺寸。

由此可见，波动范围表示的是自相关函数与坐标轴所夹的面积。

本文针对算例边坡，给出了4种不同水平与竖向波动范围组合下的抗剪强度参数随机场，如图3所示。图3中每一种随机场模型都可视为一种可能的实际情况，每一个单元的中心参数视为本单元的参数，以不同的颜色区分参数的大小。很明显，从图3中可以看到所得计算范围内的抗剪强度参数是不均匀的，且不同的波动范围组合所得到的随机场参数分布也不同，体现了抗剪强度参数的变异性及模拟方法的随机性。从图3中还可以看出，当δx=10δy时，抗剪强度参数高强度带与低强度带近似成条状分布；当δy=δx时，高强度带与低强度带近似呈块状分布。此外，波动范围越大，高强度带(或低强度带)越连续。一般来说，岩土体参数在空间上的各向异性，由于受地层沉积作用、土体堆积作用等影响，水平方向的相关距离大于垂直方向的相关距离[11]，如水平方向的相关距离变化范围一般为10～40 m，而垂直方向的相关距离变化范围为1～3 m。

图3 不同的竖直向和水平向波动范围组合下的随机场实现Fig.3 Realizations of random fields for various com-binations of horizontal and vertical fluctuation scales

考虑到渣料场为人工逐渐堆填的，具有较明显的成层特征，同时也考虑渣料本身构成由不均匀的渣体组成，因此本文的分析中取 ，水平方向波动范围取40 m，垂直方向波动范围取4 m。

3.3 稳定性分析结果

在土体参数为均值时，如图2所示的边坡稳定性安全系数为1.286。在考虑边坡土体抗剪强度参数空间变异性的情况下，对该边坡抗剪强度参数的空间分布进行了1 000次随机模拟，相应地计算得出1 000个可能的安全系数及其滑动面位置。将该1 000个安全系数进行平均，均值为1.290，与边坡土体抗剪强度参数取均值时的安全系数接近。

计算结果表明，在考虑抗剪强度参数空间变异性的情况下，算例边坡的安全系数概率密度近似呈正态分布，其中最小安全系数为0.985，最大值为1.902，是抗剪强度参数空间随机组合出现的极端情况，出现概率极低，大部分计算结果介于1.1～1.4之间，如图4所示。

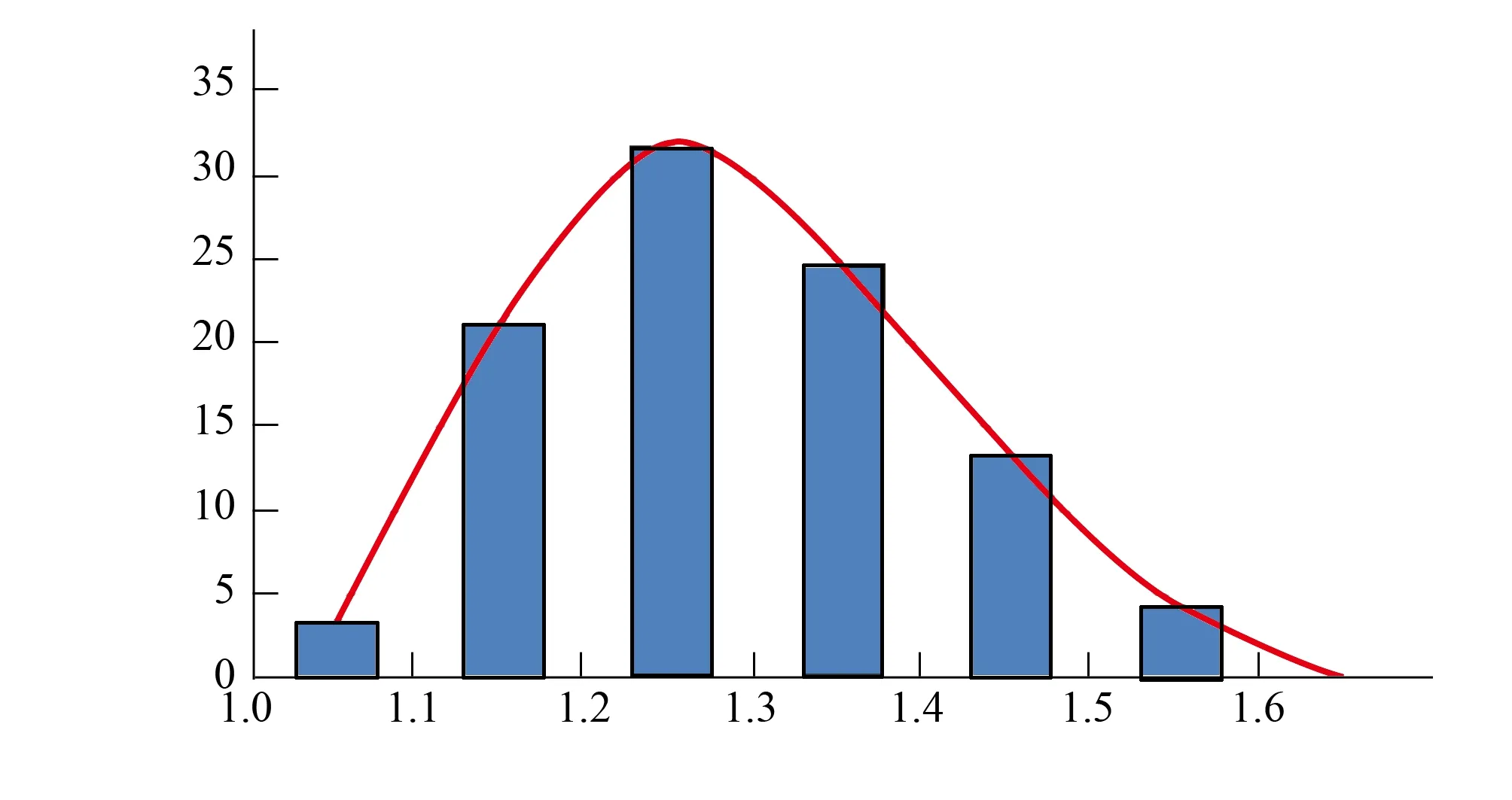
图4 边坡安全系数概率分布图Fig.4 Probability distribution chart of safety factor

由图4还可以看出，在考虑土体抗剪强度参数空间变异性时，53.3%的边坡实际安全系数小于边坡土体参数为均值时的安全系数，极端情况下边坡甚至存在破坏的可能。如果以1.25作为稳定安全系数，则不考虑抗剪强度参数的空间变异性时，该边坡是稳定性的(1.286)；而考虑抗剪强度参数的空间变异性后，安全系数小于1.25的概率为44%，即确保该边坡稳定的概率只有56%。

本算例的分析结果说明采用本文方法能够考虑土体抗剪强度参数的空间变异性对边坡稳定性的影响，在实际工程中考虑土体抗剪强度参数空间变异性影响也是必要的。

4 工程实例

4.1 工程概况

某水电工程渣料场位于该工程下游河道左侧，该渣料场在原设计渣料场基础上扩容形成，总渣料方量达到60万方。该渣料场共分为4～5个平台，平台宽10～30 m不等。由此可见该渣料场范围大，堆填不规则。为确保该地区生态环境安全，需要对该渣料场进行安全防护和水土保持治理。从安全角度来看，该渣料场除应进行整体稳定性分析外，尚应进行分区稳定性分析。受文章篇幅限制，本文选取该渣料场某一分区的典型断面进行稳定性分析，如图5所示。

图5 某水电工程渣料场局部现状图Fig.5 Current situation of abandoned dreg site in a hydropower project

4.2 计算参数

该渣料场位于河谷地带，地势相对平坦，避开了冲沟、泥石流等不良地质作用区。本项目渣料块石含量较高，经过现场踏勘、测量并结合当地经验，取饱和状态下渣料的重度为21.2 kN/m ，黏聚力c的均值为10 kPa，内摩擦角φ的均值为33°。此外，与算例相同，黏聚力c的空间变异系数取0.3，内摩擦角φ的空间变异系数取0.2；水平的波动范围δx=40 m，垂直波动范围δy=4 m。该渣料场最终的物理力学参数及计算参数取值见表2所示。

表2 渣料计算参数取值表Tab.2 Properties of slag

4.3 稳定性分析

根据现场测量资料绘制该渣料场边坡计算断面图如图6所示。该部分渣料场边坡坡高为24 m，分为两级，第一级边坡高10 m，坡度i=0.78，第二级边坡高14 m，坡度i=0.83，中间马道宽度为4 m。考虑到原地形比较平缓，且抗剪强度参数均高于渣料参数，因此为简化分析，计算断面不做区分。

图6 典型计算断面示意图Fig.6 Typical section of abandoned dreg site

由于渣料大部分由石渣构成，孔隙率较大，难以形成稳定的地下水，因此考虑暴雨或久雨工况时，只按照饱和参数进行分析，不考虑渗流作用。若不考虑该渣料场边坡渣料抗剪强度参数的空间变异性，则其安全系数为1.354，大于允许的临界安全系数1.25。考虑渣料抗剪强度参数的空间变异性时，随机生成1 000种抗剪强度参数的空间分布，经过1 000次模拟计算，获得1 000个安全系数及相应的滑动面。将获得的安全系数进行平均，均值为1.367，与渣料抗剪强度参数为均值时的安全系数相近。在1 000次模拟分析中，该渣料场边坡安全系数的最小值为1.104，最大值为1.724，但二者出现概率极低，大部分结果介于1.2～1.4之间，其中小于1.25的占23.3%，小于1.354的占61%，说明确保该边坡稳定的概率为76.7%，均值参数计算结果的保证率仅为39%。

渣料抗剪强度为均值时的滑动面如图7中的实线所示，考虑渣料抗剪强度空间变异性时最小的安全系数对应的滑动面如图7中虚线所示。由图中可以发现两者的滑动位置基本相同，滑动深度(面积)比较接近，后者略大于前者，可能由于极端情况下，渣料抗剪强度参数均取小值，近似均匀分布，从而使其滑动位置和滑动深度均与均值参数计算结果近似，但安全系数则小得多。

图7 均值滑面与最小安全系数滑面对比图Fig.7 Comparison between slip surface of homogenous slope and critical slip surface

事实上，在考虑渣料抗剪强度参数空间变异性的情况下，对于相同的安全系数随机场，也可能存在不同的滑动面。本文挑选了边坡安全系数为1.211的3个典型的滑动面进行比较分析，3个滑动面的示意图如图8所示。从图8中可以发现，3个滑面中最大的滑动体断面面积为162.52 m2，最小的滑动体断面面积为45.21 m2，二者相差明显，说明考虑渣料抗剪强度参数空间变异性时，滑动面也不是唯一的、确定的。

图8 同一安全系数对应的多种滑面形式Fig.6 Multiple critical slip surface with the same safety factor

本例计算结果说明，对于渣料场边坡仅通过均值抗剪强度参数进行稳定性分析难以保证其安全性和准确的滑动面位置和规模等，需考虑渣料抗剪强度参数的空间变异性，进行综合的稳定性分析和评价。

5 结 语

本文通过自相关函数构建岩土体抗剪强度参数的随机场，利用改进的乔列斯基分解法离散抗剪强度参数随机场，并利用非侵入式随机有限元方法分析岩土体抗剪强度参数空间变异性对边坡稳定性的影响。通过算例分析验证了本文方法的合理性和正确性，最后将本文方法应用于实际的水电工程渣料场边坡稳定性分析，分析结果可供该渣料场防护设计参考。主要结论如下：

(1)利用改进乔列斯基分解法离散随机场，计算过程简单，编程易于实现，离散出的随机变量与有限单元一一对应，便于理解，是一种行之有效的模拟方法。

(2)非侵入式随机有限元方法在考虑岩土体抗剪强度参数的空间变异性时，可利用确定性有限元软件进行分析，无需重新编程，计算效率高。

(3)考虑岩土体抗剪强度参数的空间变异性时，边坡的稳定性安全系数近似成正态分布，其平均值与采用均值参数的计算结果相近。统计结果表明采用均值参数计算所得的边坡稳定性安全系数的保证率不足50%。

(4)考虑岩土体抗剪强度参数的空间变异性时，计算所得边坡滑动面与参数随机分布有关，不同的参数分布可能得到不同的滑动面，即使计算所得安全系数相同，对应的滑动体面积也可能相差若干倍。

(5)工程实例分析结果表明，单一的安全系数不足以评价渣料场边坡的稳定性。对于水电工程渣料场这一特殊的人工边坡，应考虑渣料抗剪强度参数的空间变异性，并结合工程实际进行稳定性及滑动面的综合分析和评价。