人类竞赛运动中速度分布及其偏度与能耗的关联探究

胡金洁，林振权

(温州大学数理与电子信息工程学院，浙江温州 325035)

2005年Barabasi发表在Nature上关于人类行为时间上阵发现象的2篇文章[1-2]开启了关于人类自身复杂性与多样性的实证研究，越来越多的关于人类动力学的研究，在时间和空间行为规律的探索上都取得丰硕成果.通过对邮件通信[2]、网页浏览[3-4]、手机短信[5]等行为发生间隔时间的研究，发现其很好地服从幂律分布[6-9]；在空间行为上，通过对人类迁移[10]、银行账单传递[11]、GPS数据[12-13]统计等空间行为的研究，发现其分布也存在无标度特性[14].

关于人类动力学行为的机制探索，与各种人类动力学行为的实证研究同步进行.研究人员提出多种模型对人类非泊松特性行为的动力学机制进行理论探究与分析，取得了显著的成果，并且在相关方面已经产生了应用价值.首先是基于优先权的排队模型[1]，考虑到重尾的基本条件，对于有优先决策权的任务序列，添加新的条件或者对模型参数取值进行调试来对应不同的实际情况.其后有基于任务驱动的动力学模型[15-16]，对任务队列提出3种不同的处理方案；基于兴趣模型[17]，反映人类行为会受兴趣的影响；基于记忆驱动模型[18]，反映记忆效应对人类行为的影响，研究人类行为发生频率对以后发生概率的影响；基于习惯的动力学模型[19]，反映人类的心理对人类行为的影响；价值驱动模型[20]、偏好返回模型[21]等等.

人类动力学的时间行为和空间行为的交叉，与人类在空间上运动速度有关的人类动力学的速度行为，对于人类的复杂生活，如疾病传播、交通和通讯网络发展等具有重大影响，但限于相关数据的缺乏，这方面的研究非常稀少.2000年Savaglio等在Nature上发表基于各种赛程的跑步和游泳世界纪录数据研究全程平均速度与赛程长短关系的实证统计[22]，指出随着赛程增大，跑步和游泳运动世界纪录平均速度与时间纪录存在双幂律关系，赛程较短的几种跑步（如 ≤ 1 000 m的男子、女子跑步）和游泳的世界纪录平均速度随时间纪录的线性下降快于赛程较长的几种跑步（如 ≥ 1 500 m的男子、女子跑步）和游泳.进一步的研究揭示速度纪录随时间纪录下降快慢不同的前后两个赛程阶段（较短阶段和较长阶段）分别对应于比赛过程中运动员能量消耗的无氧运动和有氧运动模式.最近，有学者从马拉松跑步参赛者比赛时间入手实证研究具有相互影响的人类群体行为中的速度行为[23-24]，对美国纽约城市马拉松赛参赛者群体的速度分布的统计分析发现参赛者群体全程速度分布符合对数正态分布，而在其8个中间计时赛段中，速度分布从初始阶段的对数正态分布变化到中间赛段的高斯分布，到最后阶段变化到对数正态分布.研究还发现中间计时赛段中速度分布的变化与各赛段内比赛的竞争激烈程度存在关联性.

我们进一步拓展关于具有相互影响的人类群体行为中的速度行为的实证研究.选取具有悠久历史的滑雪、跑步、自行车赛等著名的比赛作为研究对象，实证统计滑雪、跑步和自行车比赛中参赛者全程平均速度分布特性，以研究不同种类运动中群体速度分布的差异，并探索其机制.发现这三类不同比赛中参赛者的速度分布偏离正态分布情况有很大差异，滑雪与跑步的速度分布为右偏态分布，而自行车赛的速度分布为左偏态分布.进一步探索三种不同运动速度分布差异与其运动特性差异的关联，发现三类比赛速度分布的偏度与比赛的单位路程能量消耗存在正相关.

1 数据

我们实证统计分析典型的滑雪、马拉松跑步和自行车赛的速度分布（本文仅取各比赛的男子组），选取的各比赛项目的数据特征如表1所示.

表1 数 据Table 1 Data

2 滑雪、跑步、自行车运动的速度分布及其偏度的统计分析

为了统计滑雪、跑步、自行车运动的全程速度分布特性，对每项运动的每场比赛的每位参赛者的比赛成绩（完成全程时间）都进行处理分析.对于一项运动某一年的一场赛事，根据总的路程除以每个人的比赛时间得到该场比赛中每一个参赛者的全程平均速度vi（i=1,2,3,…,N，N是完成全程比赛的总人数），然后将所有参赛者按其速度进行装箱处理（binning）以减小数据涨落，即将速度轴划分为宽度相同的一个个连续的区间（速度箱），各运动的速度装箱宽度已列于表1.对于每个速度箱，计算全程平均速度处于该速度区间内所有参赛者速度的平均速度v和该速度箱内参赛者人数占该场比赛总人数的比例值P(v).以各速度箱内参赛者的平均速度v为横坐标，参赛人数比例值P(v)为纵坐标，应用Origin软件画出平均速度v-人数比例P(v)数据图.图1为典型的滑雪、马拉松跑步和自行车赛的速度分布图，从图1可以看出，滑雪、跑步、自行车三种比赛的速度分布图偏离标准正态分布（Gauss分布）情况明显不同，滑雪运动速度分布图有很明显的右偏趋势，跑步运动整体上为右偏趋势，但是偏离程度明显小于滑雪比赛，而自行车运动有很明显的左偏趋势.

速度分布曲线的右偏、左偏或偏离程度很小，其速度分布函数完全不同.为此，首先定量计算三种运动速度分布的偏度.偏度概念在数理统计中定量描述统计数据相对平均值分布非对称程度的量，具体定义为：

其中，和σ分别是N位参赛者全程速度vi的平均速度和标准差.当统计数据S>0时为右偏分布，且S值越大，右偏的程度越高；当统计数据S<0时为左偏分布，且S值越小，左偏的程度越高；当统计数据S=0时为对称分布，如高斯分布（标准正态分布）.

应用Origin软件对三种运动的速度分布数据进行拟合，以调整的R2值最大为标准确定最优拟合分布函数，发现滑雪比赛的全程速度分布都可以用pulse函数很好地拟合，其分布函数为：

其中参数A为振幅（A>0），v0为速度分布起始点，v1和v2为宽度（v1,v2>0），a为幂.马拉松跑步比赛的速度分布总体上符合对数正态分布.文献[24]表明美国纽约马拉松跑步全程速度分布从2001年到2016年基本都是对数正态分布（仅在2009年、2010年、2013年和2014年是正态分布，但是也可以很明显观察到分布右侧有很长的尾巴）.对数正态分布表达式为：

其中，μ和σ分别是lnv的平均值和标准差.自行车赛的速度分布可以用正态分布（Gauss函数）更好地拟合，其表达式为：

其中，μ和σ分别是v的平均值和标准差.

通过计算滑雪、跑步和自行车赛三种运动的速度分布偏度，来进一步分析这三种不同运动的全程速度分布模型及其差异.选取2009-2016年赛程相差小的瑞典Halvvasan滑雪比赛（45 km）、德国Hamburg自行车赛（55 km）、美国纽约马拉松（New York city marathon）跑步比赛（42.195 km）为研究对象，统计计算结果如图2所示，2012年纽约因为天气原因取消了马拉松比赛，所以没有计算这一年的数据.从图2可以发现，滑雪比赛的速度分布偏度值在0.7至0.9之间，跑步的速度分布偏度值在0.3至0.5之间，而自行车比赛的速度分布为负偏，偏度值在-0.3至-0.1之间.综上所述，可以明显观察到三项比赛全程速度分布的偏度值不同，自行车比赛的速度分布偏度值很低，基本为负值，即左偏态分布；跑步、滑雪比赛的速度分布偏度值高于自行车赛的，为右偏态分布，滑雪比赛偏离正态分布程度大于跑步运动，与图1中各项运动的偏度情况是一致的.

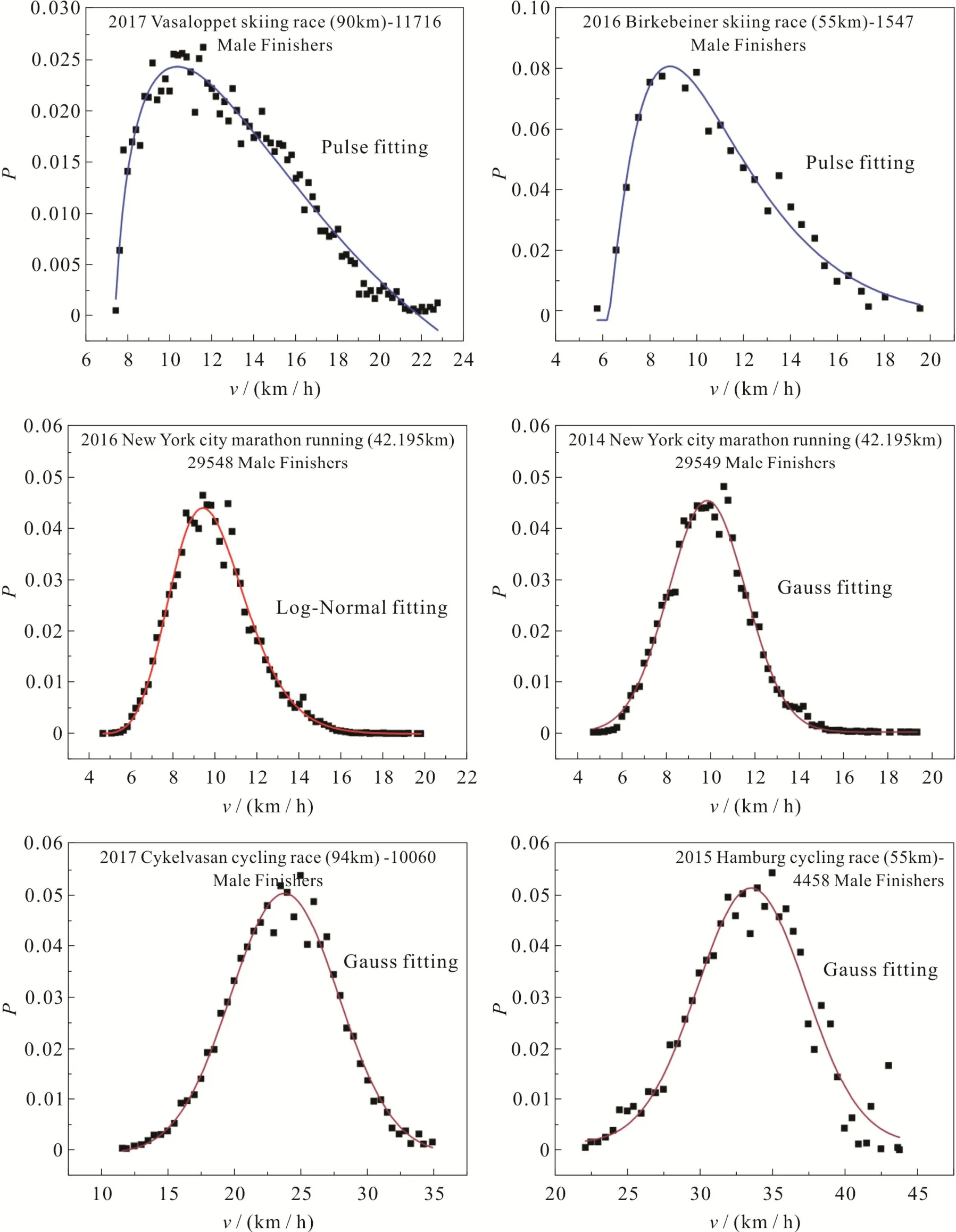
图1 瑞典Vasaloppet、美国Birkebeiner滑雪比赛，纽约马拉松跑步比赛和瑞典Cykelvasan、德国Hamburg自行车赛全程速度分布Fig 1 Velocity Distribution of Sweden Vasaloppet and America Birkebeiner Classic Skiing Race, New York City Marathon Running, and Sweden Cykelvasan and Germany Hamburg Cycling Race

3 速度分布偏度与运动能耗的关联

滑雪、跑步和自行车赛三种运动中参赛者速度分布曲线和偏度存在明显差别，这必然与三种运动的某些特性的差别相关.我们尝试探索三种运动的能耗情况与其速度分布偏度的关联，以图从运动本身特点寻找其速度分布曲线和偏度的特性.

对于跑步，Loftin等人[25]对业余马拉松跑步参赛者完成比赛的摄氧量（VO2）和能耗有过深入研究，所考察男子选手的完成全程平均时间为（241.3 ± 4.06）分钟，单位时间摄氧量为（3.78 ±0.32）L / min，全程摄氧量912.1 L，单位路程能耗为（66.3 ± 4.8）kcal / km，全程能耗为2791.8 ±235.3 kcal.刘春辉[26]等采用间接热量测定法测定青年运动员在步行、跑步以及骑自行车过程中的能量消耗情况，根据相关及回归分析分别建立这些运动的摄氧量与速度（speed）和体重（BM）的方程，其中男子跑步的能耗方程为：

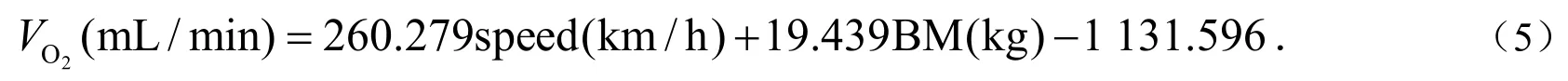
根据纽约马拉松跑步比赛2009-2016年全部运动员的实际数据（见表2）按公式（5）（取体重为70 kg）推算男子马拉松跑步的单位时间摄氧量为2 842.34 mL / min，再利用Loftin等人对业余马拉松跑步参赛者完成比赛的摄氧量和能耗的研究数据[25]，推算业余马拉松跑步的摄氧量和能耗之间的关系为1L摄氧量相当于3.36 kcal能耗，按此当量计算的男子马拉松跑步的能耗为9.55 kcal / min，全程能耗为2 496.12 kcal，单位路程能耗为59.16 kcal / km.

分析发现Loftin等人招聘测试的马拉松赛选手完成全程平均时间241.3 min快于纽约马拉松2009-2016年全部运动员的平均成绩261.37 min，考虑到能耗随速度增大，故按（5）式计算的稍小的能耗（单位路程59.16 kcal / km）比较符合纽约马拉松赛的实际数据.

对于滑雪运动，Christensen等[27]对瑞典滑雪运动员的研究给出几个不同速度时的摄氧量与能耗数据，两者与速度呈很好的线性关系，我们对其做线性拟合得出摄氧量以及能耗（EE）与速度的关系分别为：

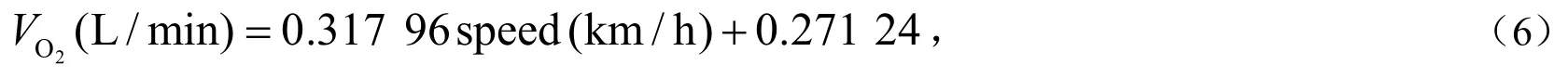
和

据此关系根据瑞典Halvvasan滑雪比赛运动员实际速度（11.88 km / h）推算得出业余滑雪运动员最大单位时间摄氧量约为4.05 L / min，全程能耗为5 014.53 kcal，单位路程能耗为111.43 kcal / km（具体见表2）.

对于自行车赛，刘春辉等[26]建立的男子自行车赛摄氧量方程为：

其中FFM为运动员的去脂体重.王道等人[28]对不同速度自行车骑行气体代谢与能量消耗的研究也给出了与上面一致的结果，即运动员的单位时间摄氧量和单位时间能耗均随骑行速度近似线性增加，1L摄氧量对应的能耗当量随骑行速度呈缓慢的线性增加.我们对该能耗（EE）/ 摄氧量的当量随速度做线性拟合给出关系为：

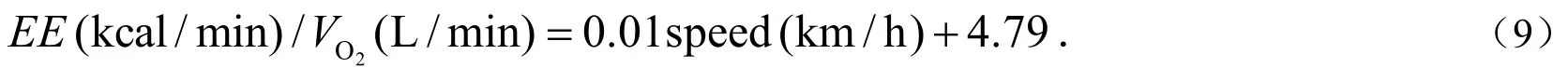
对德国Hamburg自行车赛实证统计数据如表2所示.（8）中运动员去脂体重取为60kg，将运动员平均速度代入（8）和（9）估算得出自行车赛摄氧量为2 998.74 mL / min，能耗 / 摄氧量的当量为5.12 kcal / L，单位时间能耗为15.35 kcal / min，自行车赛全程能耗为1 575.90 kcal，单位路程能耗为28.65 kcal / km.

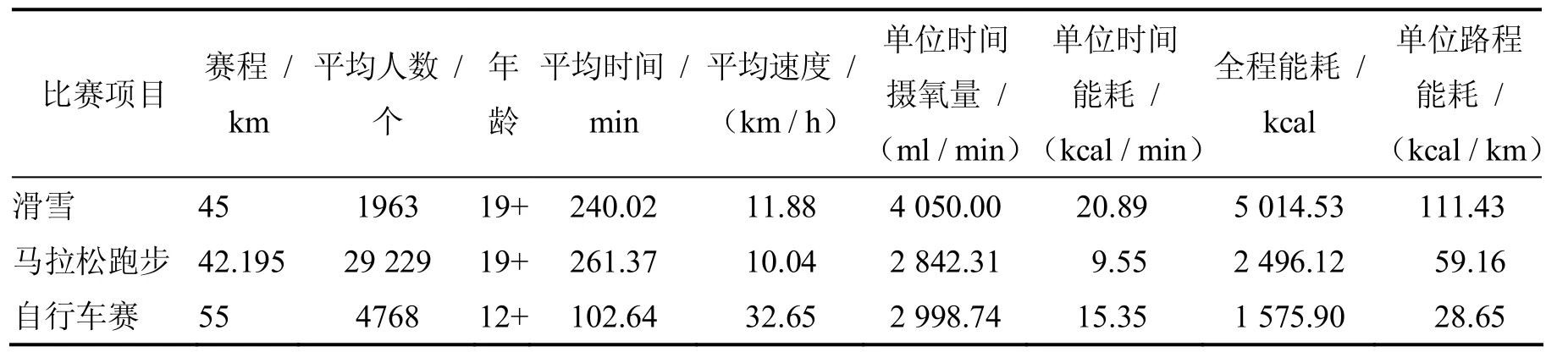
表2 滑雪、跑步和自行车赛能量消耗情况Table 2 The Energy Consumption in Skiing, Running and Cycling Rice

表2计算数据是2009-2016年间全部参赛者的各年平均成绩对应的摄氧量和能耗.按照以上计算方法，我们计算2009-2016年间每年瑞典Halvvasan滑雪比赛、美国纽约马拉松跑步比赛和德国Hamburg自行车赛的单位路程能耗，结果示于图3以与图2的滑雪、跑步和自行车赛全程平均速度分布的偏度值变化对照.每年的平均速度分布的偏度值与单位时间摄氧量及单位路程能耗的关系分别见图4和图5，线性拟合的调整的R2值列于图中.

图2 滑雪、跑步和自行车赛平均速度分布的偏度Fig 2 The Skewness of the Velocity Distribution of Skiing, Running and Cycling

图3 滑雪、跑步和自行车赛的单位路程能耗Fig 3 The Energy Expenditure (EE) of Skiing,Running and Cycling

图4和图5显示，速度分布偏度与能量消耗关联明显强于速度分布偏度与摄氧量关联.进一步采用Pearson相关性定量分析其关联强度，两种关联的Pearson系数分别列于表3和表4.

对比表3和表4可以发现每年的滑雪、跑步和自行车赛全程平均速度分布的偏度值与单位路程能耗呈很好的线性关系，二者的Pearson相关系数各年平均为0.962，说明二者具有很强的相关性.各年平均速度分布的偏度值与单位时间摄氧量的相关系数均低于偏度值与单位路程能耗的相关系数，各年平均为0.726，说明单位时间摄氧量对速度分布偏度影响不明显.由此，可得出关于不同种类运动（滑雪、跑步和自行车赛）速度分布的初步结论：滑雪、跑步和自行车赛参赛者全程速度分布的差异是由于每项运动单位路程能耗不同引起的，速度分布的偏度与该项运动的单位路程能耗存在很强的关联性.

图4 滑雪、跑步和自行车三种运动速度分布偏度与摄氧量关联图Fig 4 The Correlation between the Skewness of Velocity Distribution and the Oxygen Uptake (VO2) in Skiing,Marathon Running and Cycling

图5 滑雪、跑步和自行车三种运动速度分布偏度与能量消耗关联图Fig 5 The Correlation between the Skewness of Velocity Distribution and the Energy Expenditure (EE) in Skiing, Marathon Running and Cycling

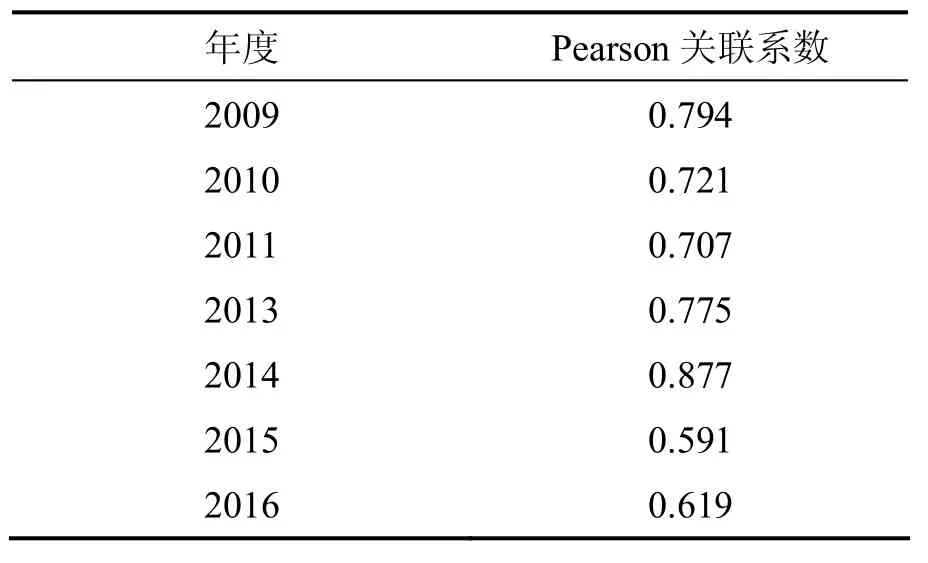
表3 平均速度分布偏度值与单位时间摄氧量的Pearson关联系数Table 3 The Skewness of Average Velocity and Pearson Correlation Coefficient of Oxygen Uptake per Unit Time

表4 平均速度分布偏度值与单位路程能耗的Pearson关联系数Table 4 The Skewness of Average Velocity and Pearson Correlation Coefficient of Energy Consumption per Unit Journey

4 结论与讨论

本文通过对滑雪、马拉松跑步和自行车赛三种不同运动的参赛者全程平均速度分布的实证统计，发现三种运动的速度分布曲线偏离正态分布的情况存在很大差异，滑雪和跑步的速度分布曲线为右偏态分布，而自行车赛的速度分布曲线为左偏态分布.进而选取赛程相差较小的瑞典Halvvasan滑雪比赛（45 km）、美国纽约马拉松跑步比赛（42.195 km）、德国Hamburg自行车赛（55 km）为研究对象，统计计算这三种运动2009-2016年期间每年的速度分布偏度值，发现滑雪和跑步的速度分布偏度值分别在0.7-0.9和0.3-0.5之间，自行车赛的速度分布偏度值在-0.3至-0.1之间.在此基础上，进一步探索这三种运动的参赛者速度分布与其运动特性的关联，具体为考察这三种运动的速度分布偏度与其摄氧量和单位路程能耗的关联，研究发现每年的滑雪、跑步和自行车赛全程平均速度分布的偏度值与其摄氧量的关联较小，而与其单位路程能耗呈很好的线性关系，二者的Pearson关联系数各年平均为0.962，由此获得关于这三种运动速度分布的初步结论：滑雪、跑步和自行车赛参赛者全程速度分布的差异是由于每项运动单位路程能耗不同引起的，速度分布的偏度与该项运动的单位路程能耗存在很强的关联性.这一关联分析结果无疑加深了对人类群体运动行为及其机制更深刻的认识.