运动模糊角度检测的两种改进方法

周 军，韩 森,2

（1．上海理工大学 光电信息与计算机工程学院，上海 200093；2．苏州慧利仪器有限责任公司，江苏 苏州 215123）

引 言

随着科学技术的发展，各种摄影设备在我们的日常生活中被广泛应用，例如智能手机、各种相机以及各种监控设备，使我们获取图像的手段越来越多。由于在获取图像的时候会受到气流扰动、机身震动、运动速度、器材设定等因素的影响，实际获得的图像会产生模糊以致影响图像的识别效果。尤其是对运动物体进行图像识别时，更需要将模糊的数字图像复原成清晰的图像。

图像复原的关键点就在于点扩散函数的估计(PSF)，因其直接关系到图像复原的效果。对于PSF的估计，国内外学者提出了很多的方法。文献[1-3]分析了模糊图像频谱图条纹的规律信息，给出了相应的检测算法，如Hough变换和EM算法。文献[4]用拉氏算子对模糊图像进行无方向性的二阶微分，且利用了微分图像的自相关结果，但计算量大，抗干扰能力不强。文献[5]对图像频谱的暗条纹直接进行Radon变换计算其方向角度，但此方法对条纹不清晰、对比度较小的频谱图像检测精度差，抗干扰能力不强。文献[6]采用频谱块与边缘检测相结合的方法，虽然能避免中心十字亮线，但是也裁剪了很多有用的信息。因此，对于运动模糊图像频谱图中的十字亮线影响模糊角度检测的问题，本文提出了两种改进方法。

1 运动模糊模型

通常一幅退化图像(即模糊图像)可以看成是一幅清晰图像与退化函数的卷积，考虑噪声干扰的影响(一般假设噪声是加性的)，则这个图像的退化过程(模糊过程)可以用数学表达式表示为

式中：g(x,y)为退化的图像；h(x,y)为退化函数，也就是点扩散函数(PSF)；f(x,y)为原图像；η(x,y)为加性噪声； ⊗为卷积运算符。图像一般都由二维离散的数据组成，在实际应用中，退化模型写成如下形式：

式中：M、N分别为图像的长和宽。

在没有噪声干扰的情况下，即

空域中的卷积关系对应于频域中的相乘关系，所以可以得到频域模型

假设原图像f(x,y)做直线运动，x(t)和y(t)分别是x轴和y轴方向上的运动时间变化分量，并且假设曝光时间为T，噪声为0，则有

g(x,y)表示运动模糊后的图像，若将表达式两边分别进行频域变换，则可以求出其频域表达式如下：

若令模糊长度为L，模糊角度为，则该模糊图像的点扩散函数为

根据上式可以看出，复原模糊图像的关键点在于点扩散函数的求解，而点扩散函数的求解关键在于模糊长度L和模糊角度的求解。

2 模糊角度估计

2.1 模糊图像频谱非中心化检测模糊角度

王琳等[7]采用频谱块与边缘检测相结合的方法，该方法将模糊图像频谱图分块，裁剪去中心十字亮线部分，如图1所示。

图1 运动模糊图及其频谱图和裁剪图Fig.1 Image of motion blur and its spectrum with and without magnification

可见裁剪过后，虽然去掉了十字亮线，但也裁剪掉了很多有用的信息，如图1(c)所示，导致检测精度不高。

针对十字亮线问题，本文提出了提高Radon变换检测模糊角度的一种改进方法(改进方法一)，其具体方法为：将模糊图像的频谱图非中心化，则十字亮线被分散到四个角落里，再进行裁剪，这样既保留了原图的主要信息，又剪去了十字亮线；接着用Canny算子进行边缘检测，从而提高了Radon变换的检测精度，改进结果如图2所示；随后对图2(d)进行Radon变换，求模糊角度，如图3所示(图中Rt表示灰度值叠加求和，表示矩阵R相对应的坐标位置，表示旋转角即Radon变换中对图像进行投影的方向)。

图2 改进方法一图Fig.2 Image obtained by method 1

图3 Radon 变换一Fig.3 Method 1 after Randon transformation

根据上述分析，我们的改进方法一步骤如下：

(1)对模糊图像g(x,y)进行二维离散傅里叶变换得到频谱图G(u,v)，为了增强其频谱图条纹的清晰度，我们取其频谱图谱再进行对数运算G′(u,v)= |lg(|G(u,v)|+1)|。

(2)将G′(u,v)非中心化，则得到一个新的频谱图B(u,v)。

(3)对新的频谱图B(u,v)进行裁剪，得到D(u,v)(将四个边角上的十字亮线裁剪掉，裁剪掉了干扰信息，大大减少了十字亮线对Radon变换的影响)。

(4)对裁剪后的图像进行Canny边缘检测，得到一个有白色线条的图像。

(5)将图像E(u,v)进行Radon变换，得到一个矩阵R，然后将这个矩阵R和旋转角画一个极值曲线，求出其最大值，最大值对应的横坐标就是其旋转的角度，则该角度就是我们所求的运动模糊角度，的取值范围为0°～180°。

2.2 用模糊图像的二次傅里叶变换检测模糊角度

上述方法是对模糊图像做一次傅里叶变换，用Canny算子检测其明暗相间的条纹信息，但Canny算子只是在图像中找出具有局部最大梯度幅值的像素点，而对于频谱图中明暗相间条纹模糊且梯度较小的时候，其边缘检测和Radon变换的误差将会非常大，如图4所示。

图4(c)边缘检测图显示不出明暗相间条纹的边缘信息，且中心十字亮线对检测精度影响较大，以致Radon变换检测误差较大。

针对这样的问题，我们对该模糊图像进行二次离散傅里叶变换(改进方法二)，以此来细化条纹，然后进行边缘检测。从图5可以发现，中心十字亮线的干扰很严重，且二次傅里叶变换的频谱图主要信息分布在中心地带(见图5(c))。通过裁剪该频谱图的中心部分，(见图5(e))，可以减少中心十字亮线的干扰，提高Radon变换的检测精度，对图5(e)进行Radon变换后即可求得模糊角度，如图6所示。

图4 模糊图像、频谱图及其边缘检测Fig.4 Blur image, spectrum and edge detection

图5 改进方法二图Fig.5 Image obtained by method 2

图6 Radon 变换二Fig.6 Method 2 after Randon transformation

根据上述分析，我们的改进方法二步骤如下：(1)求模糊图像g(x,y)的二次傅里叶频谱图。先其中为了增强条纹清晰度和压缩灰度范围，使G′(u,v)= |lg(1+|G(u,v)|)|，再次傅里叶变换其中C′(j,k)=|lg(|C(j,k)|+1)|。

(2)对C′(j,k)进行Canny算子边缘检测，得到一个二值图像D(j,k)。

(3)将上述二值图像进行裁剪，保留其中心信息，裁剪去多余的十字亮线部分，得到。

(4)对E(j,k)进行Radon变换，得到一个矩阵P，根据矩阵P和旋转角画一个极值曲线，求出其最大值，最大值对应的横坐标就是其旋转的角度，再根据换算关系，得到所求模糊角度与旋转角的关系

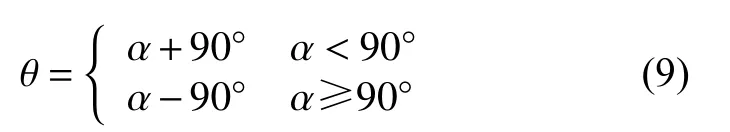
式中 α的取值范围为0°～180°。

3 实验数据与分析

为了分析和验证上述两种改进方法的可靠性，我们分别对不同模糊角度的两幅图(如图7、图8所示)进行对比实验，模糊角度和模糊长度由计算机仿真所得，所以可以有真实角度提供对比。

图7 Lena （频谱图条纹清晰）Fig.7 Lena image (clear fringes in the spectrum)

图8 Bridge（频谱图条纹不清晰）Fig.8 Bridge image (blur fringes in the spectrum)

表1数据表明：在频谱图条纹清晰的时候(图7)，直接对模糊图像的频谱图进行Radon变换可以大致检测出角度，但检测精度不高，且模糊长度越小，其检测误差越大；分块频谱图可以提高精度，但是相对于我们改进的方法一和方法二，误差比较大，检测精度没有我们改进后的高，方法一相对于方法二精度较高。

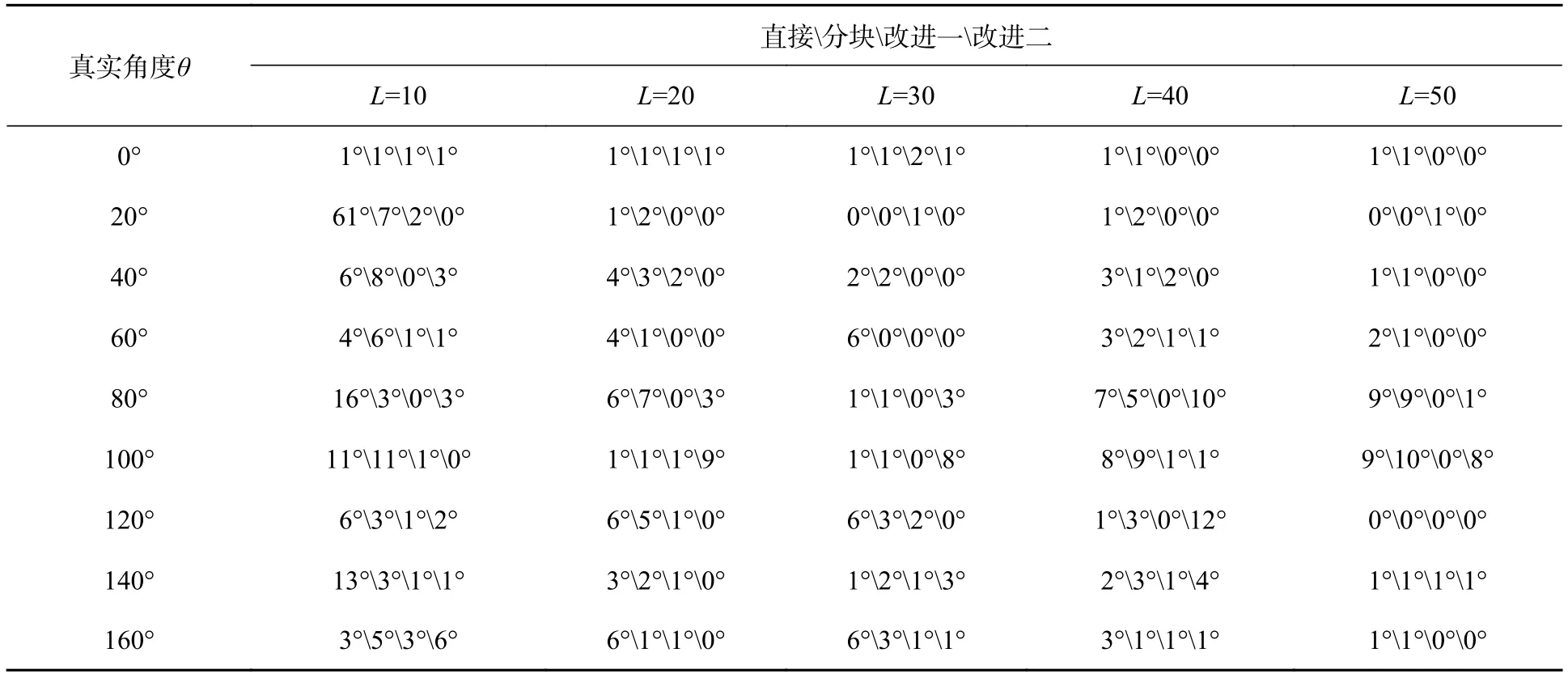
表1 运动模糊图像（图7）模糊角度检测误差对比结果Tab.1 Errors of the motion blur angle in Fig.7

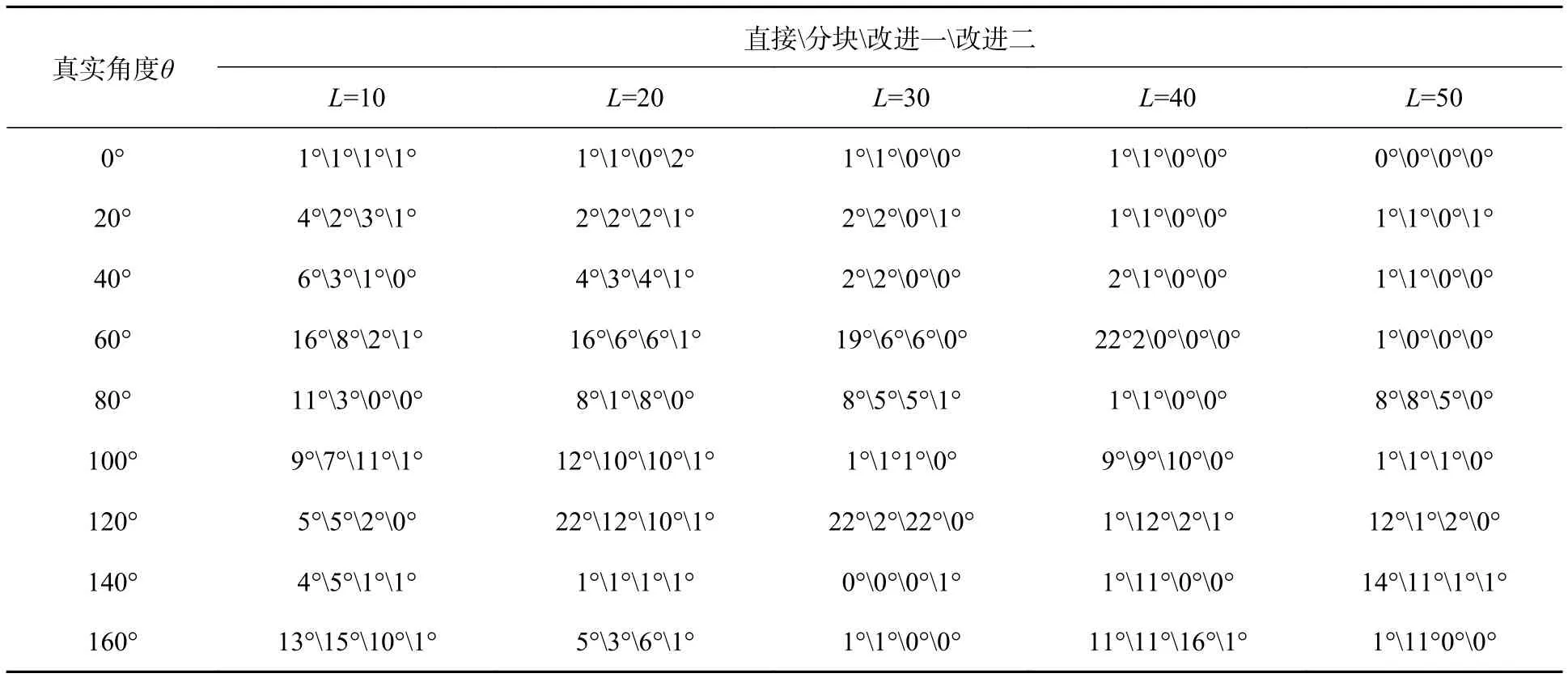
表2 运动模糊图像（图8）模糊角度检测误差对比结果Tab.2 Errors of the motion blur angle in Fig.8

表2数据表明：在频谱图条纹不清晰时(图8)，直接对模糊图像的频谱图进行Radon变换和频谱图分块的方法误差较大，且改进方法一的检测误差也非常大，说明边缘检测检测不出模糊图像频谱图的明暗相间的条纹，同时将中心十字亮线检测了出来，所以很多数据都是接近90°，而改进方法二的检测精度相对于其他的方法就很高。

对比表1、表2，我们可以发现：在频谱图条纹较清晰时，改进方法一的检测精度较高；在频谱图条纹较为模糊时改进方法一误差较大，而改进方法二的检测精度较高。

4 结 论

运动模糊图像的复原，其PSF的获得直接影响图像的复原效果，为了提高运动模糊图像的模糊角度检测精度，在其他学者研究的基础上，本文提出了两种不同的改进方法。针对不同的模糊图像频谱图，给出了不同的检测方法，检测精度得到了提高。但是本文也存在着一些不足，因为在运动模糊图像的获取中一般都会存在多方向、多尺度的模糊，并且在照明条件较差的时候，也会存在大量的噪声，在后续的工作中，这些问题还有待进一步的解决。