轴对称特性的解题应用探索
黄焕才
[摘 要] 轴对称以及性质不仅是中学数学重要的知识,还是一种重要的解题工具.在解析问题时若能合理利用轴对称变换或轴对称的性质,则可以挖掘题目中的隐含条件,建立高效的解题思路.文章深入探索轴对称在几何证明、图形翻折、线段最值和函数运算中的应用.
[关键词] 轴对称;证明;翻折;路径;函数
轴对称及其性质是初中数学重要的学习内容,具有轴对称特性的图形不仅存在外在的美感,还具有内在的关联性.利用轴对称的观点去观察图形结构、分析内在联系、构造几何图形,可以挖掘题目中的隐含条件,从而降低思维难度,获得问题求解的思路,因此可以说轴对称不仅是图形的一种特性,同样可以将其作为是一种工具应用于解题.
轴对称在几何证明中的应用
几何中存在一些具有轴对称特性的图形,例如正方形、长方形、菱形、圆等,将这些图形沿着对称轴对折可以使其完全重合.利用其轴对称的性质可以获得众多的等量关系,如对应角相等、对应线段相等,在解题时充分利用这些性质可以实现等角或等线段转化,从而打开解题的突破口.
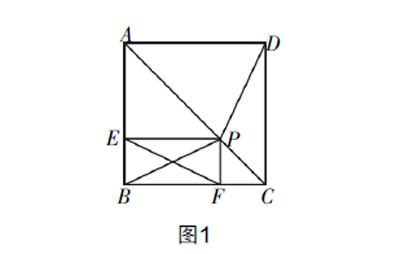
例1:如图1所示,四边形ABCD为正方形,点P为其对角线AC上的任意一点,过点P作PE⊥AB,垂足为点E,再过点P作PF⊥BC,垂足为点F,连接PD,PB,EF,试求证:PD=EF.
分析 题干所给四边形为正方形,该图形具有轴对称的特性,解题时可以充分利用.分析可知PD和EF不具备存在于两个全等三角形中的条件,不能通过求证三角形全等直接获得,因此需要综合利用图形中的性质进行等边转化.具体思路为首先利用正方形的轴对称性得出PD=PB,然后证明四边形EBFP为矩形,得出PB=EF,进而证明PD=EF.
证明 已知四边形ABCD是正方形,则顶点B和D关于对称轴AC对称,所以点P到两点的距离相等,即PD=PB. 又因PF⊥BC,PE⊥AB,所以四边形EBFP为矩形,则矩形的对角线PB=EF,从而有PD=EF,证毕.
点评 求证不相关的两条线段相等一般有两种方式:一是直接进行等边转化,二是通过求证三角形全等,利用全等性质来完成. 上述在进行等边转化时充分利用了正方形为轴对称图形的特性,实现了第一步转换,为后续的分析奠定了基础. 因此在分析问题时要充分利用轴对称图形的特性,挖掘隐含条件.
轴对称在图形翻折中的应用
翻折是图形变换的一种方式,在图形翻折中隐含着角平分、三角形全等、对称等概念和定理.实际上,翻折前后的图形关于折痕呈轴对称图形,因此在分析翻折问题时可以从轴对称角度出发,利用轴对称的观点来挖掘隐含条件,建立问题与条件之间的关联.
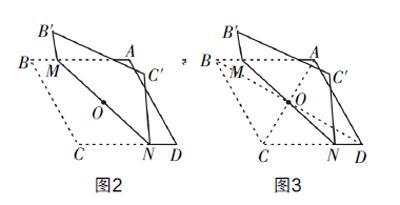
例2:如图2所示,四边形ABCD为菱形,其对角线分别为6和8,点O为两条对角线的交点.现选取过点O的一条直线MN为折痕对图形进行翻折,使点B落在点B′,若B′M=1,试求线段CN的长.
分析 点N位于菱形的边CD上,翻折前后的图形关于折痕对称,利用轴对称的性质可得B′M=BM,CN=C′N,已知菱形两条对角线的长,利用勾股定理可求得菱形的边长. 已知B′M的长度,就需要利用全等三角形进行长度转化,建立DN与BM之间的等长关系.
解 连接BD和AC,由题干可知四边形BCNM通过翻折得到了B′C′NM,由轴对称可得B′M=BM=1,CN=C′N. 菱形的两条对角线长分别为6和8,则AO=3,BO=4,△ABO为直角三角形,利用勾股定理可求得斜边AB=5,即菱形的边长为5. 在△OBM和△ODN中,有∠MBO=∠NDO,OB=OD,∠BOM=∠DON, 所以△OBM?艿△ODN,所以DN=BM.CN=CD-DN=AB-BM=5-1=4,即线段CN的长为4.
点评 翻折是一种较为特殊的图形变化,其中隐含着众多的“变”与“不变”,实际上其中的“不变”条件就可以从轴对称的角度来看,如上述图形翻折前后的对应线段长相等. 考虑到翻折所得的图形较为复杂,有时难以准确提取其中的等量关系,分析时可以首先把握图形翻折前后的对称点和折痕,则对应点到折痕上任意点的线段长相等.
轴对称在线段最值问题中的应用
线段最值问题一直都是中考的经典问题,包括单线段最值和多线段和的最值两类,对于其中的某些特殊情形可以使用将军饮马模型来求解,实际上该模型就是对轴对称变换及其性质的综合利用. 在解题首先需要对线段所涉及的点进行分类,确定动点和定点,然后通过作对称点的形式实现点的共线转化.
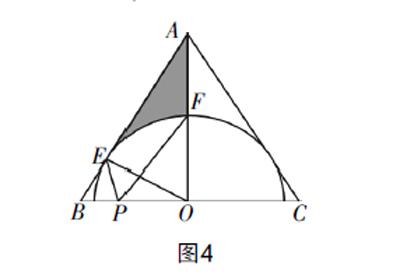
例3:在图4所示的△ABC中,AB=AC,AO⊥BC,垂足為点O,OE⊥AB,垂足为E. 现以点O为圆心,OE为半径画圆,交AO于点F,试回答下列问题.
(1)证明:AC是⊙O的切线;
(2)若点F是线段AO的中点,OE=3,试求图中阴影部分的面积;
(3)在条件(2)成立的条件下,已知点P是BC边上的一个动点,试求PE+PF取得最小值时,线段BP的长.
分析 本题目为2018年扬州市的中考几何压轴题,第(3)问是关于线段和的最值问题,求BP的长,实际上求线段和取得最小值时,点P的位置.其中点E和点F是位于线段BC同侧的两个动点,而点P是线段BC上的一个动点,显然符合“将军饮马模型”的构建要求. 只需要作点E关于线段BC的对称点G,连接FG,与BC的交点就是线段和取得最小值时点P的位置,从而可求得线段BP的长.
解 作点E关于线段BC的对称点G,连接EG交BC于点H,连接FG,与BC的交点为点P,此时点F、P和G三点共线,PE+PF取得最小值. 在Rt△EHO中,EH=EOsin∠EOH= ,BH= ,△EHP∽△FOP,由相似性质可得2HP=OP. 又因为BO=BH+HP+OP,可推得HP= ,所以BP=BH+HP= ,即PE+PF取得最小值时,线段BP的长为 .
点评 上述通过作对称点的方式,将不共线的三点转换到同一直线上,然后基于“两点之间,线段最短”原理,确立了线段和最小值的情形. 另外还可以这样理解,通过轴对称的方式实现了线段之间的转换,使得不共线的两条线段可以变换到同一直线上,为研究线段最值提供了可能.
轴对称在函数运算中的应用
抛物线是初中阶段需要学生掌握的一种特殊曲线,其特殊之处不仅体现在其函数表达式上,还体现在曲线的对称性上,即对于抛物线y=ax2+bx+c,其关于对称轴x=- 对称. 对于分布于对称轴两侧的点(x1,y1)和(x2,y2),若两点到对称轴的距离相等,则纵坐标的数值相等,即x1- =x2- ,则y1=y2,这也是抛物线中对轴对称性质的体现,同时也可以利用其对称性来比较数值大小.
例4:已知抛物线y=x2+4x-5图像上有A,B,C三点,若其坐标分别为A- ,y1,B- ,y2,C ,y3,试比较y1,y2,y3的数值大小.
分析 对于该题目常规的思路是将A,B,C三点的横坐标分别代入抛物线的解析式上,然后比较所求出的y值,但这样的思路较为烦琐,容易出错.较为简洁的方法是利用抛物线为对称曲线的特性,通过比较点到对称轴的距离大小来比较y值的大小.根据抛物线的解析式可知其开口向上,若曲线上的点到对称轴的距离越大,则对应的y值也越大,根据该思路即可对其做出比较.
解 分析可知抛物线的对称轴为x=-2,点A位于对称轴的左侧,点B和C位于对称轴的右侧,因此可先求出点A关于对称轴的对称点A′- ,y1,分析可知点A′,B,C到对称轴的距离大小为dB 点评 上述在比较抛物线上点的纵坐标值时,首先通过作對称点的方式将三点转化到对称轴的同侧,然后通过比较点到对称轴的距离直接获得了答案,该过程不仅利用了抛物线的单调性,还利用了抛物线的轴对称特性,为函数上点的坐标值大小比较提供了借鉴. 总之,轴对称及其特性在数学解题中有着广泛的应用,上述只是其中最具代表性的几例. 在分析问题时,要注意观察图形,把握几何特性和等量关系,合理利用轴对称的方式来构建模型. 实际上轴对称变换也是一种重要的思维方式,在学习时要善于利用轴对称来拓展解题思维.

