青藏高原地区3种全球DEM精度对不同地形因子的响应

高志远, 谢元礼,3, 王宁练,3, 蒋广鑫, 周 鹏

(1.西北大学 城市与环境学院, 陕西 西安 710127; 2.陕西省地表系统与环境承载力重点实验室,陕西 西安 710127; 3.西北大学 地表系统与灾害研究院, 陕西 西安 710127)

在地理学研究中，数字高程模型(digital elevation model, DEM)已成为一个重要且可靠的分析数据源，在土壤侵蚀、水土流失、流域分析、地貌分析以及地形因子提取方面有着十分广泛的应用。针对全球尺度DEM产品的精度评估工作已有不少进展。Rodriguez等人[1]利用绝对地理误差、绝对高程误差和相对高程误差等精度指标对全球6大洲的SRTM DEM数据进行精度评估；Shortridge等人[2]针对全美格局的景观结构对SRTM DEM精度影响进行了大范围的评估分析。但是对于特定地区DEM精度评价可能面临以下问题：第一，全球大尺度DEM精度评价结果不一定适用于特定区域的数字高程模型；第二，DEM精度评价主要依赖于地面测量数据如GPS测量作为验证标准[3-4]，而地面测量数据对于特殊地理环境地区通常较难获取。高精度星载雷达(ICESAT/GLAS)数据的水平精度为±20 cm，高程精度为±18 cm，已有不少学者以ICESAT/GLAS高程数据为参考进行了相关的精度分析。Enßle等人[5]利用GLAH14数据进行了树冠顶层、地面高程和植被高度的精度评价。Yue[6]利用ICESAT/GLAS高程数据对ASTER GDEM数据进行改正并与SRTM DEM数据的进行无缝融合。Liu等人[7]利用经过ICESAT/GLAS数据纠正后的ASTER数据计算兰伯特冰川的变化率，结果表明其速率符合当期冰川的物质平衡。但是全球DEM在青藏高原地区的精度情况及其地形影响因素研究的比较少。为此，本文中选取3种的全球免费中分辨率DEM数据SRTM DEM(shuttle radar topography mission digital elevation model)，ASTER GDEM(the advanced spaceborne thermal emission and reflection radiometer global digital elevation model)以及HydroSHEDS，以星载激光雷达ICESAT/GLAS数据中的GLAH14数据为高程参考标准，针对青藏高原地区具体情况，对SRTM DEM，ASTER GDEM以及HydroSHEDS DEM这3种DEM进行整体的精度评价，并分别从坡度、坡向以及地形粗糙度等地形因子进行精度变化趋势及规律的探究。

1 研究区概况与方法

1.1 研究区概况

青藏高原是世界上面积最大的高原，同时也是世界上平均海拔最高的高原，有“世界屋脊”和“第三极”之称[8]，青藏高原总面积为2.60×106km2，平均海拔4 500 m，全球海拔超过8 000 m的14座山峰全部分布在该地区[9]。青藏高原是中国3个冻土主要聚集区域之一，分布有大量季节性冻土和部分多年冻土[10]，因为其冻土面积广泛，地表覆盖特征受植被季节性变化影响小。万杰等人[11]提出时间间隔为4 a的青藏高原ICESAT/GLAS数据和SRTM DEM数据的高程线性拟合的决定系数高达0.999 8，因此在青藏高原地区利用多年ICESAT/GLAS数据进行DEM精度评价十分合适。本文研究区为青藏高原非冰雪覆盖区域。

1.2 研究数据

本次研究使用的数据主要包括DEM数据和ICESAT/GALS数据。DEM数据包括SRTM DEM，ASTER GDEM和HydroSHEDS。SRTM DEM数据选用的是SRTM V4版本，SRTM V4版本数据是针对SRTM V2版本的缺失数据进行插值补充；ASTER GDEM为对地观测卫星Terra的近红外波段获取的立体像对生成的DEM；HydroSHEDS DEM是在3弧秒的SRTM DEM数据基础上，采用新改进和新开发的算法所生产的数据。3类DEM数据对比如表1所示。ICESAT/GLAS数据采用的是GLAH14数据，GLAH14数据是由GLAH05数据和GLAH06数据再生产的陆地表面二级测高数据。GLA14数据为散点记录方式，相邻点的距离为172 m，与目前常见的数字高程模型相比GLAH14数据有更高的精度，因此可以当成DEM的验证标准来进行精度验证。ICESAT/GLAS工作周期为2003—2009年，共18个工作时间段，数据来源于国家冰雪数据中心(National Snow and Ice Data Center， http:∥nsidc.org/)，试验中在GLAH14的18期数据序列中选取300 000余个数据点进行分析。

1.3 数据预处理

由于3种DEM数据的参考椭球体与GLAH14数据不同，要对GLAH14数据进行预处理工作。预处理工作包括高程基准处理、参考椭球体处理和粗差剔除3部分。

1.3.1 高程基准处理 在GLAH14的数据集中，直接利用HDFView工具提取出大地水准面差距的数值t，再利用公式(1)进行计算，把椭球体高程转化为正高(地面点沿过此点的重力线到大地水准面的距离)。

HT/P=h-t

(1)

式中：HT/P——TOPHEX/Poseidon椭球体的正高；t——水准面差距。

1.3.2 参考椭球体处理 3种DEM的参考椭球体都是WGS84椭球体，而GLAH14的参考椭球体是TOPHEX/Poseidon椭球体(T/P椭球体)。椭球体之间的差异主要来源于水平差异和垂直差异两方面，两者在水平方向上的差异只有厘米极[12]，因此这里主要针对高程差异进行转换。表2为TOPHEX/Poseidon椭球体和WGS84椭球体参数对比，经计算可知，两种椭球体的高程差异约在70 ～71 cm之间，一般取70 cm[13]。最后再利用公式(2)进行计算，求出WGS84的正高高程。

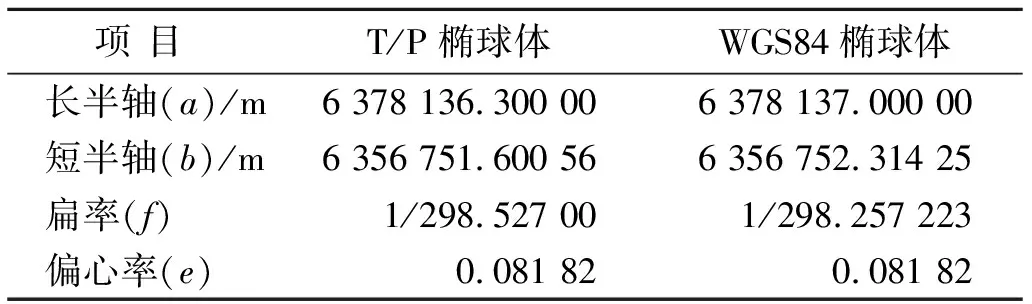
表2 T/P椭球体和WGS84椭球体参数对比

HWGS84=HT/P-0.70=h-t-0.70

(2)

式中：HWGS84——WGS84椭球体的正高；HT/P——TOPHEX/Poseidon椭球体的正高。

1.3.3 粗差剔除 先剔除NODATA的数据点(数据异常值点)，然后计算GLAH14数据点上对应的3种DEM的差值，高程差超过标准差3倍的数据点不参与统计。

1.4 精度指标

本文利用坡度、坡向以及地形粗糙度等地形因子，结合不同的精度指标，综合对3种DEM进行精度评价以及地形因子的响应分析。本文利用高程的误差d，平均误差Mean及中误差RSME作为评价精度的指标。其公式如式(3)—(5)所示。

d=hDEM-hICESAT/GLAS

(3)

(4)

(5)

其中高程误差d表示了数据集中每个DEM数据点高程与GLAH14数据之间的差值；平均误差 表示数据集中DEM数据点高程与GLAH14数据的高程误差的平均值；中误差 代表了数据集中DEM高程数据与相应GLAH14数据之间的离散程度，是评价精度的直接指标。综合研究3种DEM在不同的精度指标与各个地形因子之间的关系及变化规律。

针对DEM分形维数的计算方法，本文采用表面积—尺度法，表面积—尺度法也称作投影覆盖法，此方法由Clarke等人[14]于1986年首次提出，而后谢和平、周银军等人[15-16]又在此方法的基础之上做出了改进。首先，需要对原始的DEM栅格进行重采样，以分出不同的空间分辨率尺度Ri，并且计算每一种空间分辨率尺度下DEM的表面积Si。而后，计算各个尺度下DEM分辨率尺度Ri的对数值以及其对应表面积Si的对数值，并将其进行线性拟合，再在双对数坐标轴上找寻一段拟合较好的区域作为无标度区。虽然分形维数具有尺度不变性，但当尺度大到一定值时，粗糙表面根本不表现出分形性质[17]。因此只有当观测尺度介于一定范围内时，粗糙表面才能出现分形性质，因此需要寻找一个合适的尺度范围来计算分形维数D。

1.5 试验方案

利用以上几种精度评价指标，先计算总体精度进行统计，然后结合坡度、坡向以及地表粗糙度等地形因子进行3种DEM精度的分析。在坡度因子分析中，对坡度进行离散化分级，级差根据地形特点选取1°～5°，在每个坡度级内统计3种DEM的平均误差和中误差，分析坡度对精度的影响。在坡向因子分析中，将坡向按照45°范围分为8个坡向区域，在每个坡向区域内分别统计3种DEM的平均误差和中误差，分析坡向对精度的影响。分形维数的计算是在青藏高原研究区选取600余个ICESAT/GLAS数据点较多分布的区域，每个区域大小为60 km×60 km(图1)，因为在60 km的空间尺度下，研究区地形有较为明显的分维特征。为了保证精度，地形因子采用SRTM DEM进行计算，将每个区域的DEM栅格进行重采样，采样分辨率范围为100～600 m，以10 m作为间隔，最后利用求得的分形维数D与每个区域的中误差拟合，分析地形破碎度对精度的影响。

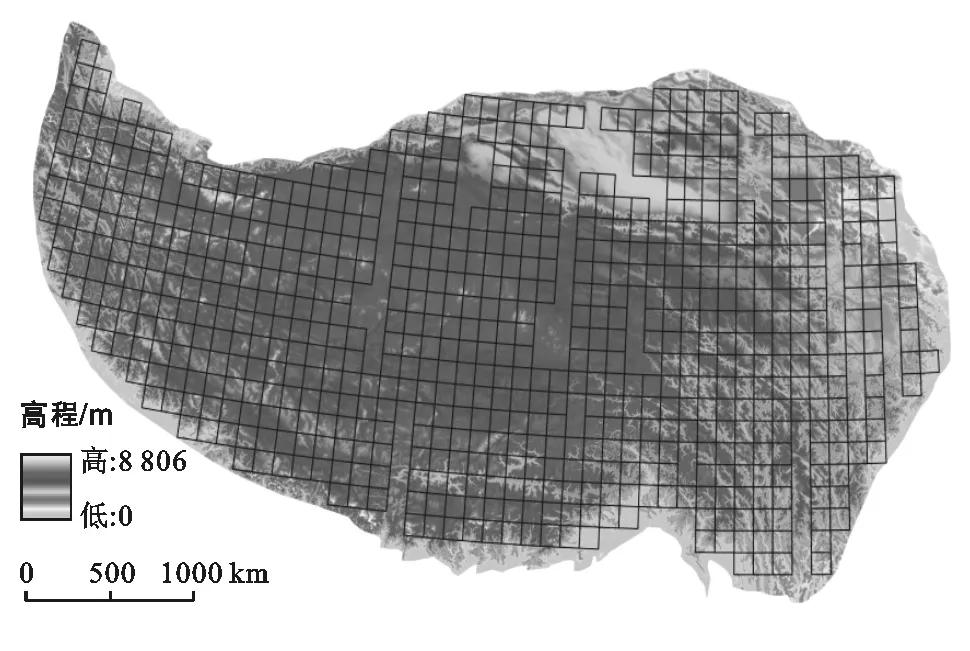
图1 青藏高原分形维数试验分区

2 结果及分析

经过统计计算，青藏高原地区SRTM DEM平均误差为0.49 m，中误差为14.29 m。ASTER GDEM平均误差为1.71 m，中误差为18.81 m。Hydro SHEDS DEM平均误差为4.17 m，中误差为31.08 m。其中，SRTM DEM数据精度与万杰等人[11]在青藏高原地区研究得到的16.65 m高程中误差相当，ASTER GDEM数据精度与杜小平等人[13]在中国西南地区高海拔山区得到的20.42 m高程中误差相接近。很明显地，在青藏高原地区，SRTM DEM精度最高，HydroSHEDS DEM精度最低。

2.1 坡度对DEM精度的影响

将DEM与GLAH14高程的高程误差d(hDEM-hICESAT/GLAS)按照点所在的坡度级进行统计，坡度级差设定为：<1°，1°～5°，5°～10°，10°～15°，15°～20°，20°～25°，25°～30°，30°～35°，35°～40°，40°～45°，45°～50°以及>50°分别求出在各个坡度级中3种DEM的平均误差Mean和中误差RSME，计算结果详见表3。

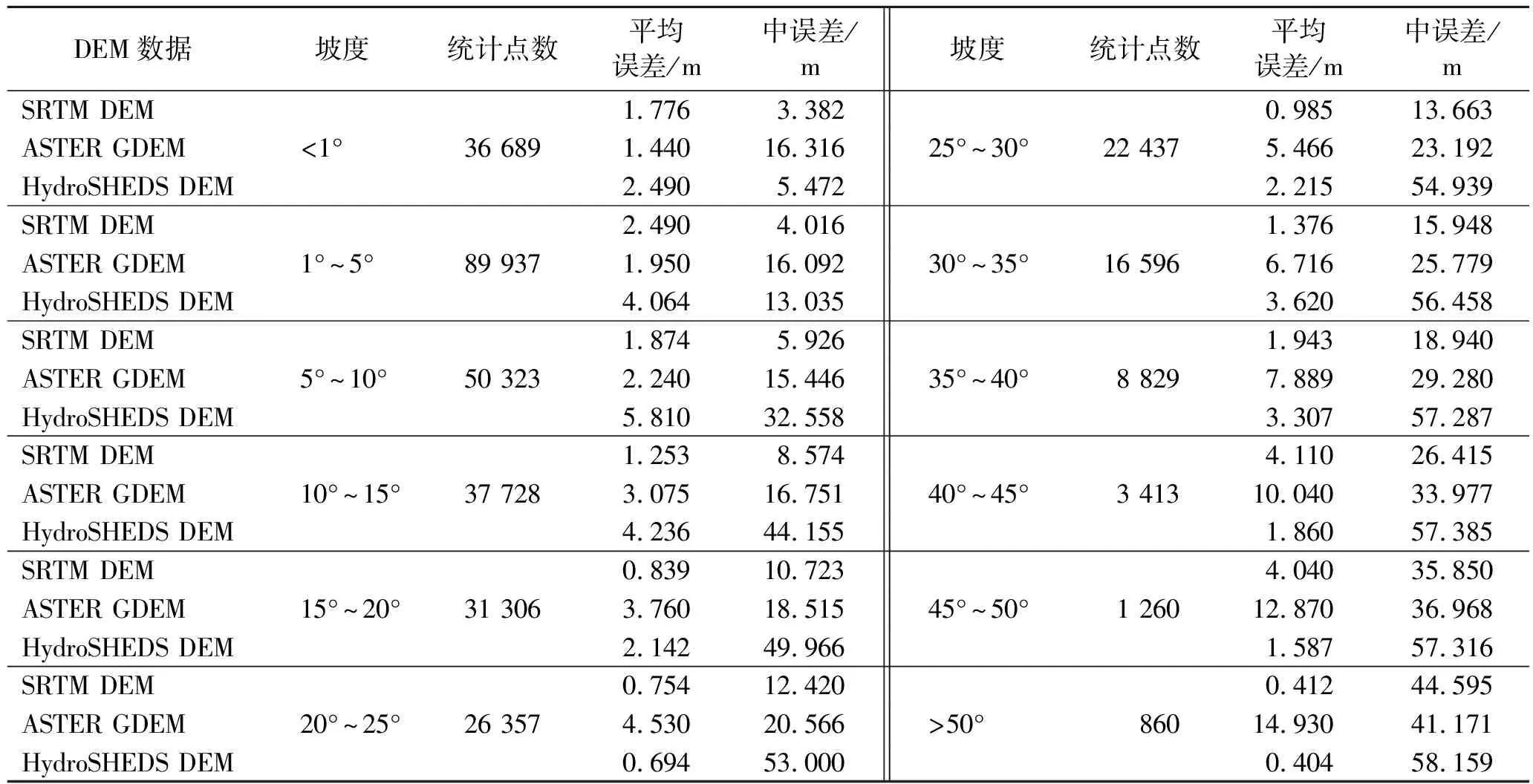
表3 各坡度区间3类DEM精度指标

3种DEM平均误差随坡度的变化及中误差随坡度的变化如图2所示。SRTM DEM的平均误差在坡度为40°～45°时较大，HydroSHEDS DEM平均误差在坡度为0°～10°及35°～45°出现两个峰值，而ASTER GDEM的平均误差随坡度增大而增大。从中误差分析来看，SRTM DEM数据高程精度在各个坡度上均优于ASTER GDEM；HydroSHEDS DEM中误差随坡度变化规律呈明显的对数关系，与SRTM DEM和ASTER GDEM的规律有很大的不同。在地形较为平坦地区(坡度小于5°)，HydroSHEDS DEM精度高于ASTER GDEM精度，但在坡度较大地区(坡度大于5°)，则ASTER GDEM精度高于HydroSHEDS DEM精度。

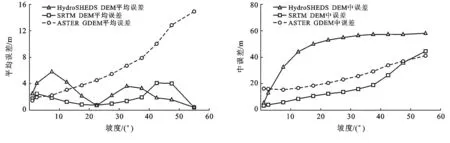
图2 3类DEM中误差和平均误差与坡度的关系

2.2 坡向对DEM精度影响

将坡向划分为北方向(337.5°～22.5°)、东北方向(22.5°～67.5°)、东方向(67.5°～112.5°)、东南方向(112.5°～157.5°)、南方向(157.5°～202.5°)、西南方向(202.5°～247.5°)西方向(247.5°～292.5°)以及西北方向(292.5°～337.5°)8个坡向级。图3为3种DEM高程误差随坡向分异图，图中上下边缘代表了除数据异常值(大于或小于上下四分位数1.5倍四分位数差的数据)外的最大和最小值。3种DEM的高程误差分布均具有不同程°的坡向分异性特征，其中SRTM DEM的分异幅°最小，不同坡向的高程误差数据中位数接近，且均大于0，高程误差随坡向的分异特征不明显，南方向和东南方向SRTM DEM的高程误差相对较大。相较于SRTM DEM，ASTER GDEM和HydroSHEDS DEM数据高程误差随坡向的分异性强，规律显著，且高程误差有明显的正负分布性。

其中ASTER GDEM高程误差正值最大值分布在东北方向和西南方向，而高程误差负值在东南方向最大；HydroSHEDS DEM的高程误差则呈现明显的“东北—西南对称”分布，坡向为337.5°～157.5°时，高程误差总体倾向为正值，且误差在东北方向和北方向值最大，当坡向为157.5°～337.5°时，高程误差总体倾向为负值，误差在西南方向和南方向值最大。可见不同DEM测量值在不同坡向上的正负分布有一定差异性。

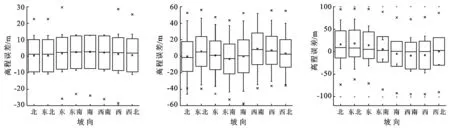
SRTM DEM ASTER GDEM HydroSHEDS DEM

图3 青藏高原3种DEM高程误差随坡向分异

为了进一步研究这种差异规律特征，本文分别对测量值大于正2倍中误差和小于负2倍中误差数据点(下文中称为正负2倍中误差数据点，即di>2RSME和di<-2RSME)按照其在某一坡向数据点所占百分比进行计算统计，尝试探究DEM测量正偏离值、负偏离值随坡向的分异特征，结果如图4所示。

3种DEM测量偏离值的分布呈现不同的特征，且程度不同。SRTM DEM正负2倍中误差数据点主要呈“南—北”分布，正2倍中误差数据点主要集中在南方向、西南方向和东南方向，其中南方向占比达3.23%，负2倍中误差数据点则主要出现在西北方向上，占比为3.07%，ASTER GDEM正负2倍中误差数据点呈现“西北—东南”分布，正2倍中误差数据点主要出现在西方向，占比为1.46%，负2倍中误差数据点主要集中在南方向，占比为0.89%。HydroSHEDS DEM正负2倍中误差数据点呈现“东北—西南”分布，正2倍差数据点峰值分布在东方向上，占比为21.52%，负2倍中误差数据点峰值位于西南方向，占比为8.69%。

研究表明，SRTM DEM测量正偏离值主要分布在南方向，而负偏离值主要分布在北方向。ASTER GDEM测量正偏离值主要分布在西北方向，负偏离值分布在东南方向，HydroSHEDS DEM测量正偏离值分布在东北方向，负偏离值分布在西南方向。3种DEM测量偏离值的离散程度不尽相同，HydroSHEDS DEM的偏离程度最大，ASTER GDEM的偏离程度最小。3种DEM出现高程测量偏离值随坡向的分异特征的原因可能与卫星传感器在上升轨道和下降轨道的航向[2]以及SRTM传感器雷达与地表的入射角度有关。

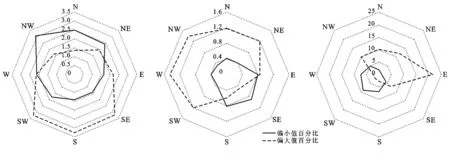
图4 3类DEM各坡向正负2倍中误差数据点占比

Zhang[18]等人在研究地表覆盖对SRTM DEM精度的影响时将坡度进行分级固定，以排除坡度因子的干扰，本文利用这一思想进行坡度、坡向的控制变量分析。不同DEM的中误差随坡向变化规律不同，且随着坡度的增加，中误差随坡向变化幅度增大，呈现更加明显的坡向分异特征。

如图5所示，当坡向固定时，3种DEM中误差随着坡度的增加，呈现增加趋势，其中SRTM DEM和ASTER GDEM在坡度大于30°时中误差迅速增加，HydroSHEDS DEM在坡度大于8°时，精度迅速变差。而当坡度处于不同的特定区间时，3种DEM精度的坡向分异规律也不同，其中SRTM DEM在各个坡度区间内中误差随坡向的分异规律均不明显，ASTER GDEM在坡度小于16°时，规律不显著，而当坡度大于16°时，坡向分异明显，且随着坡度的增加，规律愈发突出，其中最大中误差集中在西南方向，而在西北方向和北方向上精度最好，受到坡度的影响较小。HydroSHEDS DEM在坡度小于8°时，各个坡向上的精度大致相当，且中误差均在30 m以内，当坡度大于8°时，HydroSHEDS DEM中误差在不同坡向上呈现明显的“双峰”分布，即在东北方向和西南方向中误差往往较大，而在东南方向，精度相对较好。由以上分析可以发现，HydroSHEDS DEM受到地形坡度的波动精度变异性更明显，并且相对SRTM DEM和ASTER GDEM其在更小的的坡度区间内就出现了明显的坡向分异性。

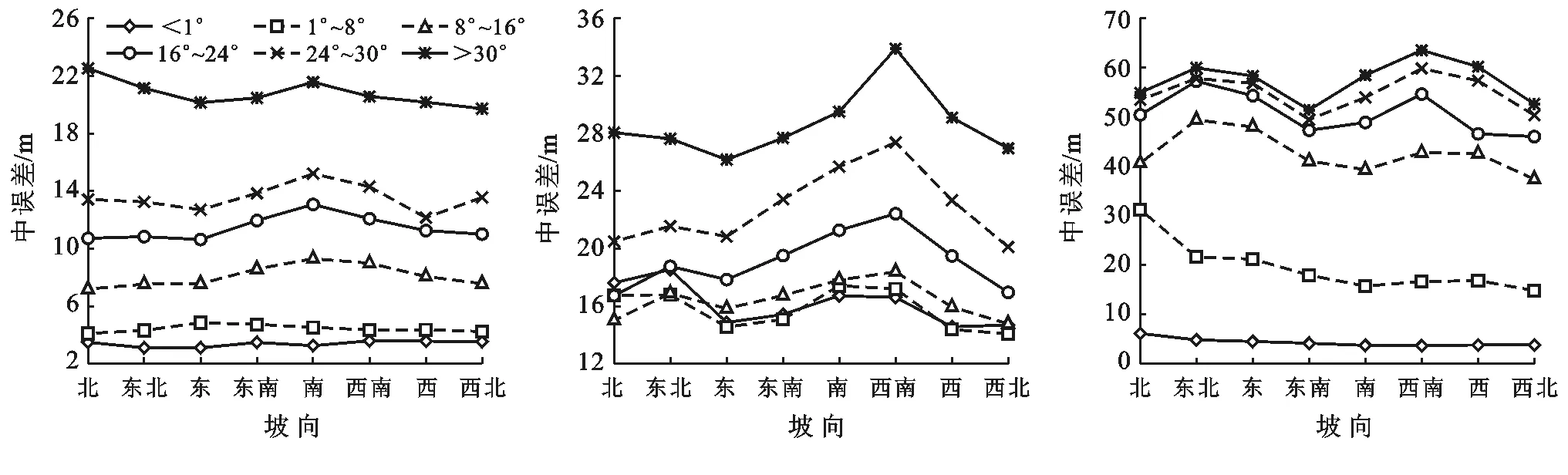
SRTM DEM ASTER GDEM HydroSHEDS DEM

图5 3类DEM各坡向中误差分市

2.3 DEM精度与地形粗糙度的关系

按照分形维数的计算步骤进行逐个样方的计算，每个样方中样点的数量从168到756，656个样方的分形维数D计算统计结果如表4所示。

表4 分形维数D统计结果

由图6可以看出，样方分形维数的分布主要集中在2.00～2.06之间，当分形维数大于2.06时，样方数迅速减少，而在2.00～2.01区间内的样方数最多，为262个，达到总数的40%。

通过对3种DEM中误差与分维数拟合，发现它们均呈现二次多项式关系，如图7所示。SRTM DEM精度受到地形破碎度的影响较小，ASTER GDEM次之，HydroSHEDS DEM精度随地形破碎度影响最大。当分形维数较大时(D>2.04)时，SRTM DEM和ASTER GDEM中误差与分维数的相关性变弱，而HydroSHEDS DEM中误差与分维数一贯的相关性，可见HydroSHEDS DEM精度对地形破碎度响应较为敏感。

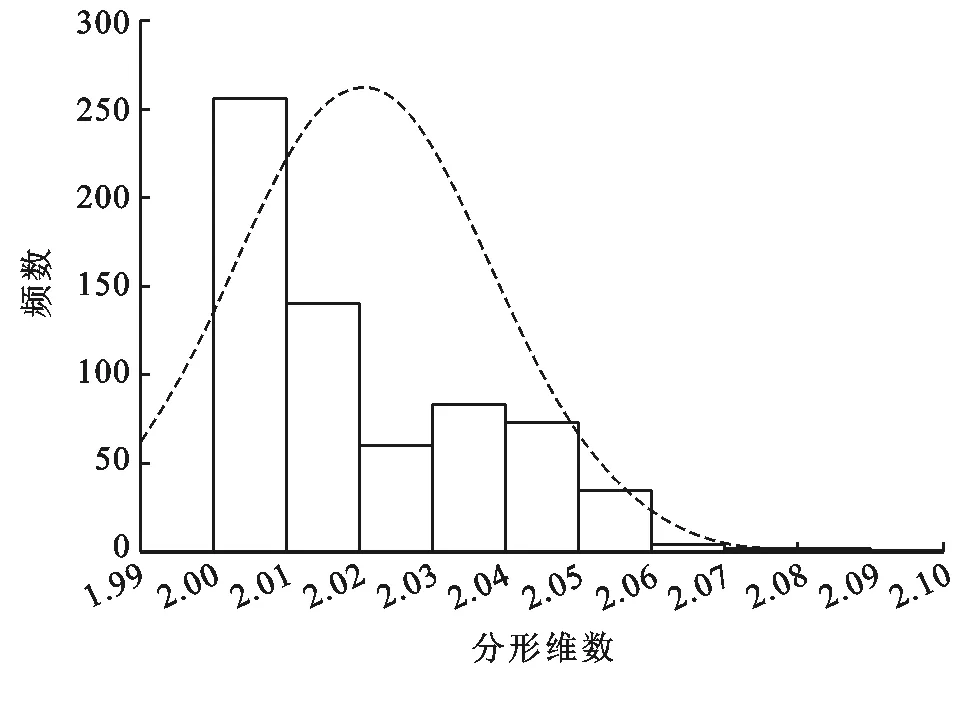
图6 分形维数数频数

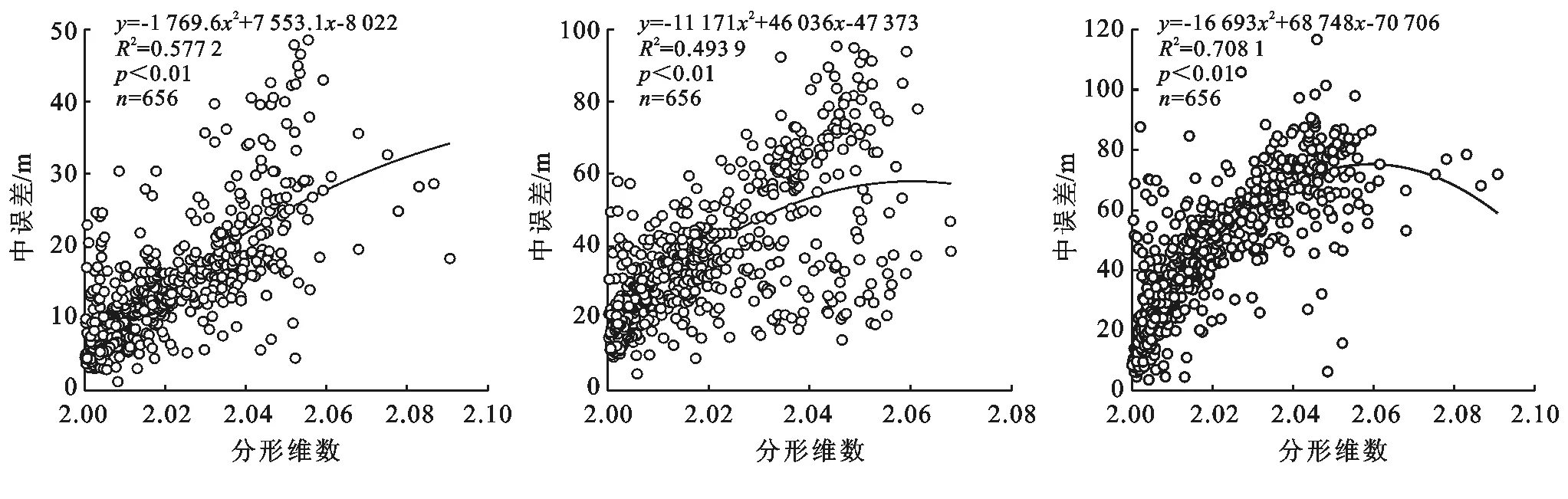
SRTM DEM ASTER GDEM HydroSHEDS DEM

图7 3种DEM分形维数和中误差的关系

3 结 论

(1) 在青藏高原地区，SRTM DEM的精度最高，中误差为14.29 m，ASTER GDEM的精度次之，中误差为18.81 m，HydroSHEDS DEM精度最差，中误差为31.08 m。

(2) SRTM DEM精度随坡度变化趋势与ASTER GDEM趋势相似，但是在各坡度区间内略优于ASTER GDEM。HydroSHEDS DEM中误差随坡度变化呈明显的对数关系，在地形较为平坦地区(坡度小于5°)，HydroSHEDS DEM精度高于ASTER GDEM精度；但在坡度较大地区(坡度大于5°)，ASTER GDEM精度高于HydroSHEDS DEM精度。

(3) SRTM DEM误差正偏离主要位于南坡向，而负偏离主要分布在北坡向；ASTER GDEM误差正偏离主要分布在西北坡向，负偏离分布在东南坡向；HydroSHEDS DEM误差正偏离主要分布在东北坡向，负偏离主要分布在西南坡向。HydroSHEDS DEM测量偏离值的离散程度最大，ASTER GDEM离散程度最小。

(4) SRTM DEM中误差在不同坡度、各个坡向上分异幅度较小，具有一定的同质性；ASTER GDEM在坡度大于16°时分异性较强，中误差峰值出现在西南坡向；HydroSHEDS DEM在坡度大于8°时分异性较强，最大中误差分布在西南和东北坡向。

(5) 分形维数D和3种DEM中误差拟合均呈较为明显的二次多项式关系，分形维数越小，分形维数对DEM精度的影响越大。其中分形维数对HydroSHEDS DEM精度影响最大，对SRTM DEM精度影响最小。