硬件损伤条件下的双跳卫星中继网络的性能分析
廖晓谈,陈鑫旺,宋 颖
(南京熊猫汉达科技有限公司,南京 210014)
1 简介
中继可以提高无线通信的范围,可靠性和质量,因此在近几十年中继研究已经成为了一个非常热的研究话题。借助于卫星中继,源端可以将信号传输到源端不能直接到达的地方[1]-[4]。
通常卫星和地面之间的通信信道可以建模为复杂的衰落信道,其衰落特征可以更加准确的描述传输信号的幅度特征,由此在文献[5]中引入了阴影莱斯信道。这个信道不仅可以更好地吻合实验数据,并且可以利于计算。
关注与此信道模型的此种特性,在文献[6-7]中,研究了单个卫星中继的放大转发系统的性能。在文献[8-9]中,单天线的视距卫星系统被研究,其中源端到中继端和中继端到目的端的信道被分别建模为阴影莱斯信道。在文献[10]中,一个相似的卫星系统讨论了中继端和目的端最佳链路问题。然而,在研究卫星中继的文献中,大多考虑的是卫星的硬件是理想的情况,然而在实际的系统中,硬件经历了多种多样的损伤,例如:相位噪声,I/Q支路不均衡和高功率放大时的非线性等问题[11]-[13]。硬件损伤在单跳网络中已经在多种情况下被研究了[14]-[16]。损伤所引起的性能的上限并不能通过提升系统的传输功率来解决,特别实在高速率的通信系统中[17]-[19],这个问题表示的更加明显。从上述的表述中,可以看出研究卫星中继通信网络中的硬件损伤是非常重要的。
到现在为止,还没有任何一篇文章来分析硬件损伤条件下的卫星中继网络,为了填补这个空白,本文研究了硬件损伤条件下的双跳卫星中继网络的性能。
文章的第二部分着重介绍了所要研究的模型,第三部分分析了硬件损伤条件下的系统的性能,第四部分给出了必要的仿真图,第五部分对全文做了一定程度的总结。
2 系统和信道模型
正如图1所示,本文考虑的是一个卫星中继网络,源端S通过中继卫星R和目的端D进行通信,并且假设源端和目的端之间不能直接通信,源端和目的端分别拥有N1和N2根天线,卫星中继R拥有1根天线,这是一个在现实很常见的卫星中继网络。本文假设所研究的信道都是阴影莱斯信道。源端和目的端分别采用了最优天线选择策略和选择合并策略,显而易见,通信过程需要两个时隙。

图1 系统模型
在第一个时隙,源端S将自己的信号发送给R。从文献[2]中可以得到,当系统是理想硬件时,接收到的信号的表达式可以表示为1i1i1iry=hs+v,1ih是从源端第i根天线到中继端R链路的独立但不同分布的阴影莱斯随机变量。1is是从源端第i根天线发送出的信号,其功率为,vr是在R端的复高斯随机变量其功率可表示为。但是当系统的节点具有硬件损伤时,接收到的信号将变化,此时接收到的信号为(1)
式中,y1i是中继端从源端第i根天线接收到的信号;η1i表示具有零均值并且功率是的硬件损伤变量;
k1i衡量的是上行链路损伤大小的变量。在第二个时隙,中继R将接收到的信号转发到D。在实际的系统中,译码转发策略通常应用在卫星通信系统中。因此在目的端D的第j根天线处接收到的信号为(2)
式中,h2i是从中继端R到目的端D的j根天线的链路的随机变量;ry是从R发出的信号,其功率可以表示为;vdj是在目的端D的j根天线处的搞死白噪声,其可以表示为;η2i表示的是下行链路的损伤噪声随机变量,其功率为衡量的是下行链路损伤大小的量。
3 系统性能分析
本部分主要分析了系统的性能,分别得到了系统的中断概率的闭式解,对阴影莱斯信道的描述和系统即时容量的分析。
3.1 系统端到端的信损噪比
同样的方法,可以知道目的端的信损噪比为
由于源端采用了最优天线选择策略,因此第一跳链路的信损噪比,可以表示为(5)
同样地,由于目的端采用了选择合并策略,因此第二跳链路的信损噪比,可以表示为(6)
由于在中继端R处应用的是处理转发策略,因此,系统的端到端的信损噪比,可以表示为(7)
3.2 阴影莱斯信道
源端到中继端和中继端到目的端的链路都用阴影莱斯信道[5]表示,由此可以得出h1i和h2j的概率密度函数,可以表示为(8)
(1)当mlp为整数时:如果:mlp是整数,那么
在文献[23]的帮助下,可以表示为
在文献[22]的帮助下,可以表示为(11)将式(11)代入(8)中,可以得到(12)
3.3 中断概率分析
通过文献[1]可知,中断概率可以表示为系统的信损噪比小于一个特定的门限的概率。在式(7)的帮助下,系统的中断概率可以表示为(13)
式中,x0表示系统的中断门限。
定理1:当mlp是整数时,可以表示为式
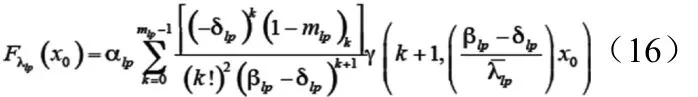
在式(5)、式(6)和式(16)的帮助下,可以将Fγ1(x0),Fγ2(x0)分别表示为(17)
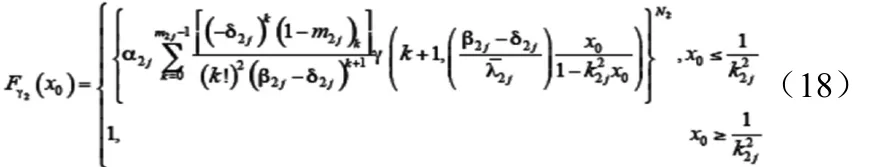
将式(17)和式(18)代入到式(14)中,式(15)
可以得到,证明完毕。
定理2:当mlp是任意数值时,可以Fγe(x0)可以表示为式(19)
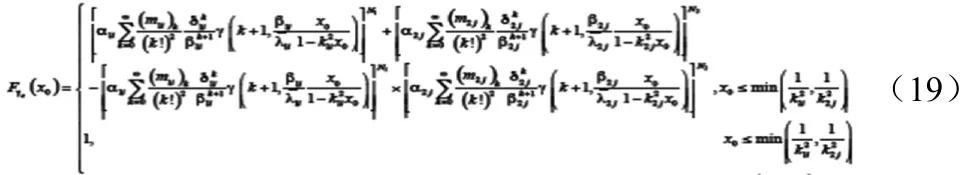
证明:在式(12)的帮助下,λlp的累积积分函数
在式(5 )、式(6 )和式(2 0)的帮助下,Fγ1(x0),Fγ2(x0)可以分别表示为式(21)和式(22)。
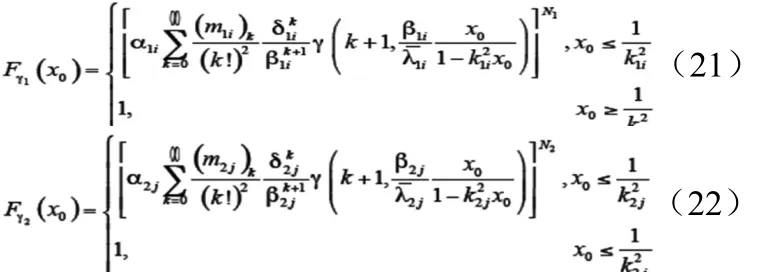
将式(21)和(22)代入到(14)中,式(19)可以得到。
3.4 系统的即时容量
这一部分研究了系统即时容量,我们给出了系统即时容量的分析解,此部分同样得到了系统在高信噪比下的近似值。
在信息论中,系统的即时容量可以数学表示为
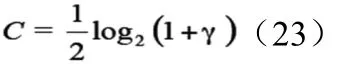
式中,γ表示为系统的信损噪比;C表示为系统的即时容量。
将式(5)、式(6)和式(7)分别代入到式(23)中,系统的即时容量可以表示为式(24)。
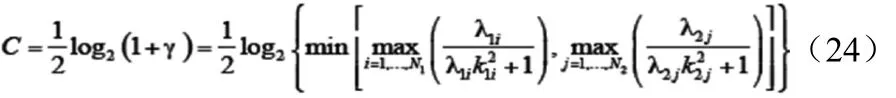
从式(24)中可以得知,当λ1i,λ2j趋向于无穷大是,式(24)将变为一个固定的值,此值仅是k1i,k2j的函数可以表示为(25)
4 仿真分析
在这一部分,仿真结果和理论值吻合,仿真验证了理论的重要性,同时仿真图直观地给出了硬件损伤对于系统性能的影响。特别值得强调的是在此部分无穷级数仅需要前30项可以和理论值吻合,同时假设P1i=Pr。
图2展示的是理想硬件和损伤硬件的性能对比图。正如图中所显示,理论结果和仿真结果很吻合同时也可以看出当信道具有深度衰落时,系统的性能将会更差,图2同时展示出系统的损伤程度小时,系统的中断概率也将变小。
图3表示的是不同的中断门限对于系统性能的影响。从图中可以看出,当系统具有硬件损伤时,系统将会出现一个中断门限,而且当中断门限增加到一定值时,系统的中断概率将恒为1。k1i,k2j的值越大,系统中断概率达到1时的中断门限越小。相反地,当系统是理想硬件时,并不存在中断门限。图4展示的系统的即时容量随着信噪比逐渐变化的曲线,从图中可以看出,在低信噪比时,硬件损伤对于系统的即时容量影响较小,在高信噪比时影响较大。同样可以看出,当系统具有硬件损伤时,正如式(25)所示,即时容量将会有一个上界,但是当系统不具有硬件损伤时,系统的即时容量,并没有上界。
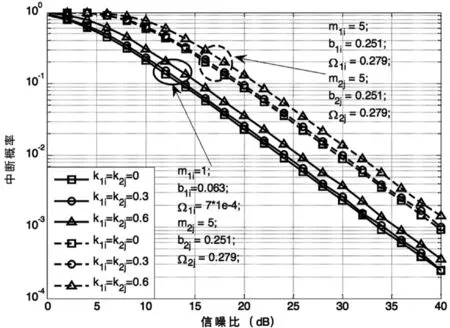
图2 理想硬件和损伤硬件的中断概率对比图
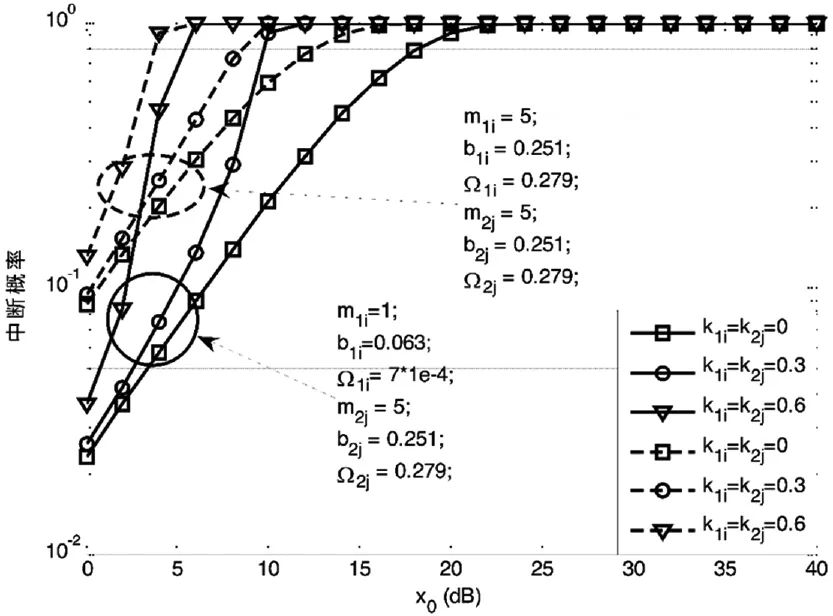
图3 中断门限对于系统中断概率的影响
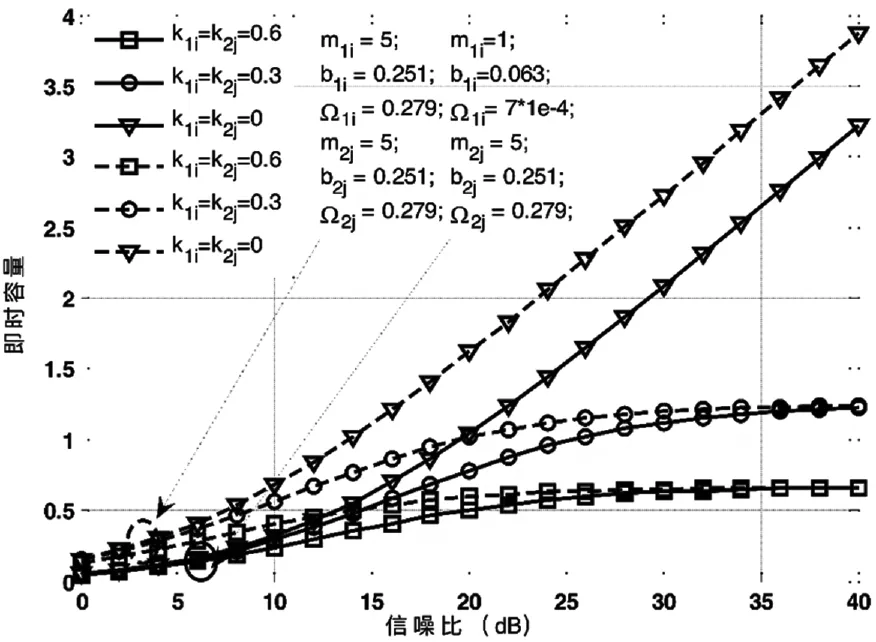
图4 不同信噪比下的系统即时容量
5 结束语
本文研究了硬件损伤条件下的卫星中继网络,特别地,我们得到了系统的中断概率的闭式解和即时容量的分析解。仿真结果显示当系统具有硬件损伤时,存在着中断门限。进一步,即时容量的分析解可以看出,当系统具有硬件损伤时,系统将会有容量的上界。同时可得出当信道具有深度衰落时,系统的性能将会更差。

