面向文本数据的正则化交叉验证方法
王瑞波,王 钰,李济洪
(山西大学 软件学院,山西 太原 030006)
0 引言
自然语言处理技术在智能系统中有广泛的应用,例如机器翻译、信息检索、搜索引擎及自动问答等,这些系统的核心模型的构建通常基于规模适中的文本数据(语料),先后经历特征提取、特征选择、模型选择及评估等阶段。模型选定后,再用较大规模的语料训练,得到模型参数的优良估计。这其中,特征选择、模型选择及评估阶段,都需要采用可靠的方法来比较模型性能(以下简称模型比较)。比如,在特征选择阶段,需要判断新特征对模型性能提升是否具有显著作用;在模型选择及评估阶段,需要判断两个模型哪个性能更好。因此,可靠的模型比较方法是文本数据建模的关键技术之一。在给定的数据集下,交叉验证方法是最常用的模型比较方法,但许多研究发现,以通常的结构化数据下的交叉验证方法来处理文本数据时,实验结果对数据的随机切分较为敏感,结果的可复现性差,结论往往不可靠。
所谓交叉验证方法,是指对给定的一个数据集进行多次切分,形成多组训练集和验证集,先使用训练集学习模型,之后在验证集上估计模型性能,最后综合多组估计来分析和推断。常用的交叉验证方法包括: Hold-out验证(将数据集切分为单组训练集和验证集)、K折交叉验证、RLT(repeated learning-testing),5×2交叉验证、组块3×2交叉验证等[1]。基于交叉验证中的模型评价指标的估计,构造t-检验统计量、Wilcoxon秩统计量等,结合统计显著性检验来进行模型比较[2]。在结构化数据上,常用的模型比较的显著性检验方法主要有: 基于5×2交叉验证的t-检验及F-检验方法[3-4]及基于组块3×2交叉验证的t-检验方法[5]。
面对文本数据时,许多研究者发现沿用通常的交叉验证方法来进行模型比较,结论往往不可靠。如,Søgaard及Berg-Kirkpatrick等指出,模型比较的结论易受文本集大小、句子长度、验证集大小及所选评价指标等因素的影响[6-7],采用通常的随机切分构建的交叉验证方案,所得出的结果并不可靠。为此,他们建议将显著性检验的p值临界值从0.05缩小至0.002 5。若显著性检验的p值小于0.002 5,则认为两模型的性能有显著差异。李济洪等[8]在构建汉语框架语义角色标注模型时也发现: 不同的框架可配置的语义角色种类、数量和句法模式是不同的。许多框架的语义角色的类别多达二三十种,交叉验证若按句子随机切分语料,可能会导致含较多语义角色的框架的句子出现在训练集中,而含较少语义角色的框架的句子被分到验证集中。这会导致语义角色标注模型的准确率(或召回率)时而偏高,时而偏低,波动较大。基于这样的结果进行模型比较,可能会导致相互矛盾的结论。再如,基于条件随机场模型的分词模型[9]中,若将大多数长句子切分到训练集中,而验证集中主要为短句子,这种句子长度分布不均匀的切分,会使分词精度有明显的差异,结果或高或低,波动较大。
综上分析,在模型比较中沿用结构化数据的交叉验证中的随机数据切分方法,很容易产生训练集、验证集“不均匀”的数据分割,从而人为地将模型性能的非实质性差异引入模型性能的评价指标估计(以下简称指标估计)中,增大了指标估计的波动(方差),难以得到模型比较的较为可靠的结论。特别是在文本数据上,现有的很多结论都基于Hold-out验证单次切分的结果,模型比较结论更不可靠。
本文的主要目标为: 针对文本数据的特点,引入正则化条件,构建带有约束的交叉验证方法,提高实验结果的可复现性,使得实验结论更为可靠。
1 构造正则化交叉验证方法的基本思路
对给定的文本数据集,从交叉验证的切分出发,应合理引入正则化条件,减小训练集、验证集的差异,降低指标估计的方差。具体可从以下三个方面着手。
(1) 如何使得训练集和验证集数据分布尽可能的一致?
理论上说,采用机器学习方法建模,要求训练集、验证集的数据分布相同,这是机器学习的一个基本要求。文本数据是非结构化的,与结构化数据相比,文本数据似乎更难达到“分布相同”这个要求。前文指出,指标估计容易受到交叉验证的切分方法的影响。随机切分形成的训练集和验证集、预测标记的分布等可能存在明显差异,导致指标估计的波动较大。为此,需要合理设计切分方法,以减少人为因素造成的差异。
(2) 如何使得不同切分的两个训练集(验证集)间的重叠样本个数尽量少且一致?
若在相同的数据集上实施多次随机切分,会使任意两个训练集间存在重叠数据,且重叠数据的个数是随机的。Markatou等[10]证明了重叠数据的个数服从超几何分布。Wang等[11-12]的研究工作表明,重叠样本个数越多,指标估计的方差也越大,且它们的关系可以用二次函数来近似描述。因此,在使用交叉验证方法时,应尽量减少任意两个训练集间重叠样本个数且尽量一致,以减小指标估计的方差。同样,在文本数据上,若交叉验证的切分中是以句子为单位,就需要使得训练集(验证集)间句子的重叠个数尽量少且重叠个数尽量相同。
(3) 如何选择适合模型比较的交叉验证方案,增加有效重复次数?
在处理独立同分布的分类和回归数据时,针对模型比较问题,许多研究表明,常用的5折和10折交叉验证方法不如5×2交叉验证和组块3×2交叉验证方法[2-5]。近期,王瑞波等仅从样本重叠个数出发,建立了正则化m×2交叉验证方法[11],证明了泛化误差的正则化m×2交叉验证估计具有方差最小性,给出了增量式的正则化m×2交叉验证构造算法。m×2交叉验证是5×2和3×2交叉验证的拓展,具体是指在给定的数据集上,重复做m次2折交叉验证,综合使用m次结果来对比模型。增大重复次数m,可以得到模型的更好的指标估计,且逐步增加实验次数,可以引入序贯检验的思想,得出更为可靠的结论。另外,m×2交叉验证的m次切分中,每一次均按对半切分数据,对于文本数据,可能更容易使训练集、验证集的分布大致相同,有利于减小分布的差异带来的影响,增大模型性能指标的信噪比(实验一)。因此,本文主要研究面向文本数据的正则化m×2交叉验证方法。
概括地说,本文针对模型比较问题,首先研究训练集和验证集分布差异对指标信噪比的影响,因为信噪比是模型比较的t-检验的本质;其次,以最小化指标的信噪比为目标,构建正则化m×2交叉验证的数据切分的优化算法,提高模型比较结果的可复现性。这在自然语言处理领域中对特征选择、模型选择以及评估具有重要意义。
2 国内外研究现状及分析
对于结构化数据集,交叉验证方法在模型性能估计、算法比较、超参数选择等方面的研究已有不少[1,13-14]。而文本数据是非结构化的,针对性的研究并不多。下面分别从结构化数据和文本数据两方面来介绍交叉验证方法在模型比较任务中的研究现状。
2.1 结构化数据上交叉验证估计的方差分析和模型比较
早期的研究工作主要集中于回归和分类问题上交叉验证估计的方差的理论表达形式。对于回归问题,McCarthy等研究了Half-sampling估计的方差理论表达式[15];Burman等给出了留一交叉验证、K折交叉验证、Repeated Learning-testing等估计的偏差及方差的理论分解式[16]。对于分类问题,Kohavi等给出了交叉验证估计的方差近似形式,并模拟分析了5折和10折交叉验证估计的偏差和方差[17]。Dietterich比较了多种模型(算法)对照方法[2]。另外,许多研究者从数据切分的角度,研究了交叉验证估计方差的理论性质[10,18-19],分析了交叉验证估计内部的相关性对其方差的影响;Rodrígue等将K折交叉验证估计的方差分解为由数据随机变化引起的方差、切分方法的随机变化引起的方差及真实误差的方差三部分[20]。王瑞波等分析了训练集间的重叠样本个数与m×2交叉验证估计的方差之间的关系[11],证明了任意两个2折交叉验证估计的协方差是关于重叠样本个数的下凸对称函数,且当训练集间的重叠样本个数均为n/4时(n为样本大小),估计的方差达到最小。
上述这些研究工作的方法,可借鉴到面向文本数据的模型比较方法中。
2.2 文本数据上针对模型比较的交叉验证方法
在文本数据分析中,交叉验证方法也被广泛使用[21]。Halberstadt明确表示不推荐将常用的交叉验证方法应用于语音识别任务建模[22],其原因是交叉验证方法的验证集分布和数据的真实分布有很大差异,挑选出不好的模型的可能性很大。同样,在基于McNemar检验的语音识别模型比较研究中,Gillick等也指出指标估计容易受到数据集分布差异的影响[23],得出不可靠的模型比较结论。
在词义消歧、词性标注等多个任务上,Daelemans等使用10折交叉验证进行算法选择和模型性能估计[24]和比较算法性能,认为算法性能之间的差异“淹没”到了误差之中,得出的结论是不可靠的。类似的结论在Berg-Kirkpatrick等、Søgaard等以及Yeh等的工作中也有详细论述[6-7,25]。这些研究工作让我们认识到: 面对文本数据集,交叉验证的随机切分,容易导致训练集和验证集的分布差异增大,加大了指标估计的方差,产生不可靠的模型比较结论。
近年来,李济洪等在语义角色标注的相关研究中也发现了类似的现象[8]。为此,他们提出用组块3×2交叉验证方法进行模型比较[5],也尝试将这种方法应用到分词、组块识别等任务的模型比较中[9,26-27]。本文中,我们的基本思想是,给定规模适中的文本数据集,使用m次重复的2折交叉验证更有利于使得训练集、验证集的分布接近,能得到更可靠的模型比较结论。
3 面向文本数据的正则化m×2交叉验证方法
对给定的文本数据集做m次切分,实施m次2折交叉验证,被称为m×2交叉验证(简记为m×2 CV)。从形式上看,m×2 CV是Dietterich提出的5×2交叉验证的扩展[2]。不过,依照5×2交叉验证所采用的随机切分来构建m×2 CV,并不适用于文本数据的建模,需要研究新的切分算法。
本文面向文本数据,研究如何构建m×2 CV的优化切分算法,以减小切分带来的训练集、验证集的分布差异,降低人为切分带来的模型性能指标估计(简称指标估计)的波动,力求使得指标估计的方差达到最小,使得基于m×2 CV的模型比较结论更为可靠。
本文的主要思想是引入合适的差异度量函数,来度量训练集和验证集的分布差异,形成控制差异的多个约束条件(简称正则化条件),以指标的信噪比最大化为目标,求解m×2 CV的优化切分算法。
在文本数据集上,许多情形下,可基于标记集合的离散概率分布差异来度量两个数据集的分布差异。比如,在语义角色标注任务中,可将语义角色类型分布看作多项分布,使用分布一致性检验的卡方统计量来度量训练集和验证集的分布差异。
3.1 记号和定义
记文本数据集为D={d1,d2,…,dn},其中,di为数据的基本切分单位(个体样本),可以是句子或篇章,依赖于具体的自然语言处理任务。例如,在文本分类任务中,di为篇章;在分词、语义角色标注任务中,di通常为句子。文本集D的索引集记为I={1,2,…,n},其中,n为D所包含基本切分单位的个数。围绕文本数据集D,下面引入一些必要的定义。


(1)

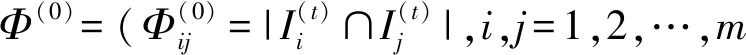
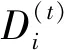

(2)
其中,式(2)右边第一项为单个二折交叉验证估计的方差,与不同训练集间的重叠样本个数无关,即与度量函数Φ(0)无关。
3.2 正则化m×2交叉验证求解的优化表示
正则化m×2 CV就是通过优化切分集合P来控制度量Φ的大小,以增大指标估计的信噪比。即,求解如下优化问题,如式(3)所示。
(3)
其中,i,j=1,2,…,m且k=1,2,…,K。

3.3 训练集、验证集分布差异的度量函数
对于大多数自然语言处理任务,在文本数据上,预测标记(如语义角色类型)及特征(如词性、词)大多是离散的,本文使用两离散随机变量分布一致性检验的卡方统计量来度量训练集与验证集之间的差异。
(4)

3.4 正则化参数如何选

4 m×2交叉验证的正则化切分集合的构造算法
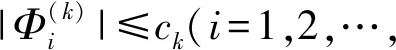
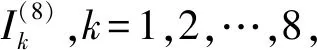
m×2 BCV数据切分的一般构造算法及对应的性能指标方差的估计方法,请参考Wang等的工作[11]。
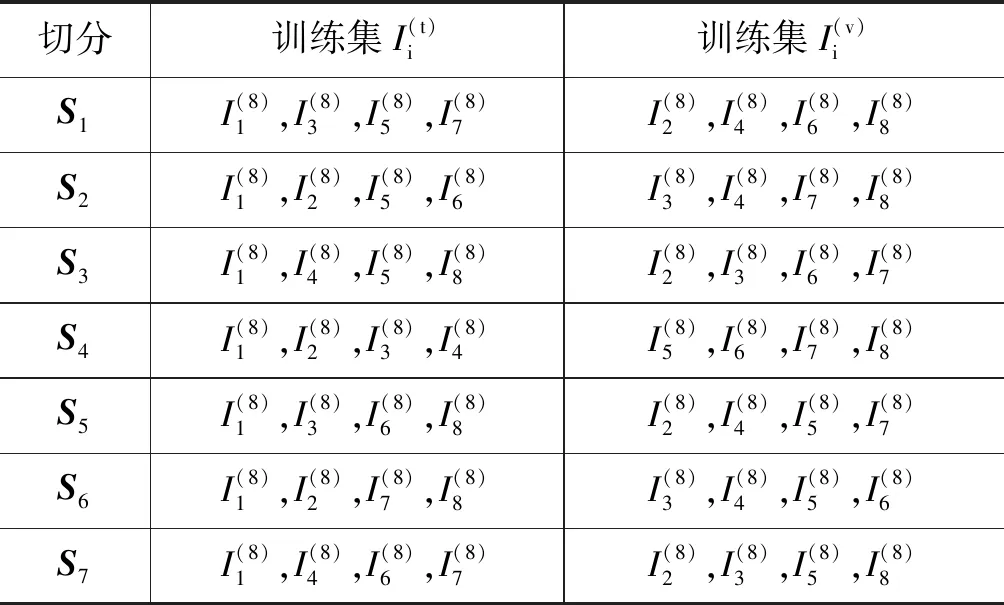
表1 7×2 BCV切分方式的拼合规则
5 基于正则化m×2 交叉验证的序贯t-检验
采用合理的统计显著性检验是得到可靠结论的保障。在自然语言处理的大部分文献中,大多在验证集或测试集上直接比较实验结果的绝对大小,或采用基于5折(10折)交叉验证的统计检验。但正如Wang等所指出的,通常基于5折(10折)交叉验证的统计检验是激进的[5],因为这些检验通常假定5次(10次)训练、测试相互独立,采用5次(10次)实验结果的样本标准差来刻画指标估计的变差。这往往造成其真实没有显著差异而推断有显著差异。为此,本文推荐一种用于模型性能比较的正则化m×2交叉验证序贯t-检验方法。该检验方法较为保守,可以得到更为可信的结论。具体描述如下:
记E=EA-EB为两个模型性能之差,EB为基线模型的性能。
原假设H0:E≤0;备择假设H1:E>0。
记模型性能指标之差的m×2交叉验证估计如式(5)所示。
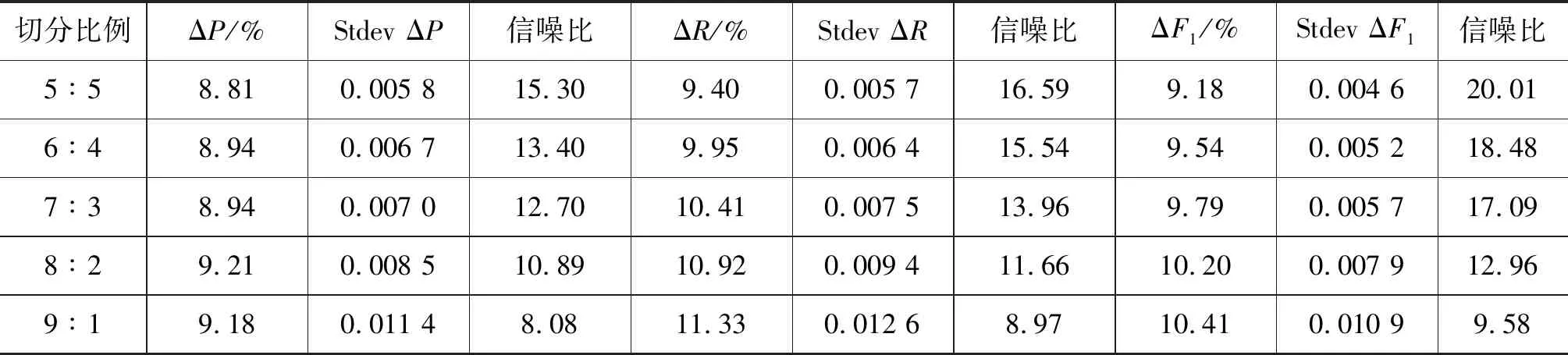
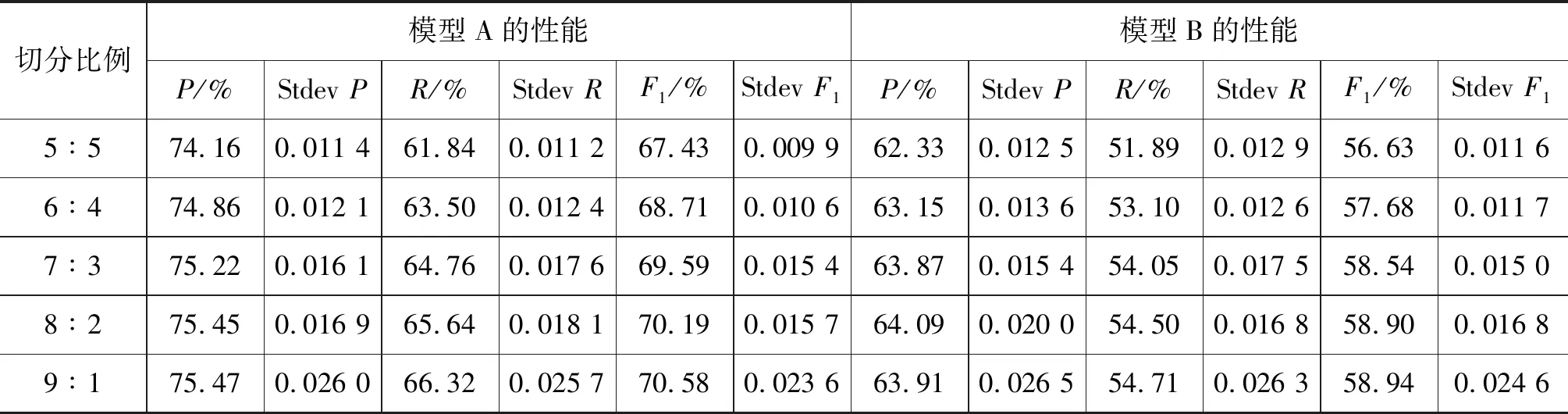
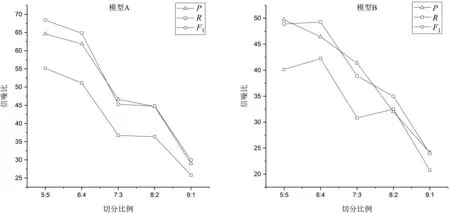
2.4.3 共有峰的指认及相关分析 根据MS离子峰及碎片信息与保留时间,综合对照品MS信息及文献报道的MS数据[11-14]对药材样品的指纹图谱中的共有峰进行结构归属的初步判断。通过与混合对照品MS图谱的离子峰信息进行比对,确定峰4、8、9、11、14、24、25分别是没食子酸、氧化芍药苷、没食子酸甲酯、丹皮酚原苷、芍药苷、苯甲酰氧化芍药苷、丹皮酚;推测鉴定出了29个共有峰,详见表4。
(5)

(6)
其中,
(7)
(8)
Tm×2为近似服从自由度为2m-1的t-分布统计量,其置信区间如式(9)所示。
(9)
该置信区间长度的期望的极限值如式(10)所示。
(10)
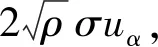
(1) 设定m=mstart;

(3) 若停止策略不成立:
① 判断m值是否达到预设最大值mstop。
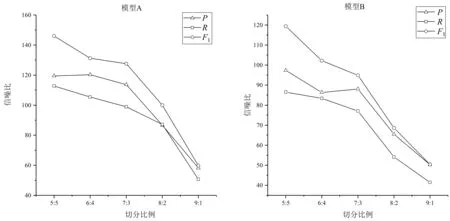
② 若m ③ 若m≥mstop,则停止实验,并接受原假设H0,即: 认为两模型性能差异不显著; (4) 若停止策略成立,则停止实验H1,并接受备择假设H1,判决两模型性能有显著差异。 其中,mstart和mstop为切分次数m的开始值和最大结束值。通常,我们推荐mstart=3,mstop=20。 Tm×2统计量本质上是信噪比的估计。因此,本文的目标是以最大化信噪比为目标,寻找合适的正则化交叉验证方法,以排除其他因素的干扰,在文本数据上得到更为可靠的模型比较结论。 本节以汉语框架语义角色标注的实验为例,说明不同的交叉验证方法所导致的词元分布差异、角色分布差异,及其对指标估计的均值、标准差和信噪比的影响。这里,信噪比定义为: 信噪比=性能指标的期望/样本标准差 实验语料来自于汉语框架语义知识库(CFN)1.0中的认知域框架例句。本文选取了6 692条例句,涵盖25个框架。实验中,我们分别考虑了语义角色识别任务和语义角色标注任务。语义角色识别任务的目标是给定一条汉语句子及目标词,识别出该目标词所搭配的语义角色块的边界。该任务并不考虑语义角色的类型,因此可以在整个语料上建模。对于语义角色标注任务,在识别出语义角色块的同时,还要标注该语义角色块的类型。由于CFN中每个框架的语义角色类型不同,语义角色标注任务只能对每个框架单独建模。 本文将语义角色边界识别和语义角色标注任务均看作以词为单位的序列标注问题,采用条件随机场(CRF)模型,并结合BIO标注策略建立模型。所用特征包括词、词性、位置及目标词。实验设置与文献[8]相同。本文采用准确率P、召回率R以及F1值来评价模型性能。在对比两个不同的模型时,本文使用ΔP、ΔR、ΔF1表示两模型性能指标的差。 基于上述实验设置,围绕交叉验证及正则化方法,本文主要回答如下三个问题: (1) 语料的不同切分比例如何影响模型性能指标的估计? (2) 训练集和验证集的分布差异如何影响模型性能指标的信噪比? (3) 正则化m×2交叉验证与随机m×2交叉验证,哪个更适合于文本数据? 为了验证语料的不同切分比例对各指标估计的影响,将实验语料按训练集与验证集的5∶5,6∶4,7∶3,8∶2,9∶1的不同比例随机切分,并重复随机切分100次,分别计算所比较的两个模型(记为模型A和B)性能的样本均值、标准差、信噪比,以及这两个模型性能差异的样本均值、标准差及信噪比。 本实验中,我们首先考虑语义角色识别任务。模型A是指文献[8]的基于最优模板(#1)的模型,模型B是指将该最优模板中的词特征(及对应的组合特征)去掉后的模型。 表2给出了不同切分比例下,模型性能的各项指标及相应的标准差。其中,P、R、F1为准确率、召回率和F1值在100次切分上的平均值;StdevP、StdevR、StdevF1分别表示准确率、召回率和F1值在100次切分上的样本标准差。表2表明,随着数据切分比例的变化,指标的均值和方差都逐渐增大,但方差增加相对较快。图1分别给出了模型A和B的信噪比。图1表明,随着训练集比例变大,信噪比在明显下降;当5∶5切分时,模型性能的信噪比最大。 表2 语义角色识别任务中语料不同切分比例对模型性能指标估计的影响 图1 语义角色识别的性能指标的信噪比 表3给出了模型A和B的性能指标之差的均值、标准差及信噪比。同样可见,按5∶5切分时,准确率、召回率和F1值信噪比达到最大。 本文进一步围绕语义角色标注任务来验证切分比例对性能指标估计的影响。考虑到“陈述”框架动词词元(简记为“陈述_v”)具有较多的例句(1 103条),实验主要分析了该框架的语义角色标注模型。模型A采用了文献[8]给出的最优模板(#12);模型B去除了该最优特征模板中与词有关的特征。表4给出了相应的实验结果。 表4表明,随着数据切分比例的变化,指标的均值和标准差都逐渐增大,其中,标准差增大较快。从信噪比角度来看(图2),随着切分比例的变化,信噪比同样在明显下降。切分比例为5∶5时,各指标的信噪比达到最大。表5是两模型的性能指标差,同样表明,在按5∶5切分时信噪比达到最大。 表3 语义角色识别任务中模型性能差异的均值和方差 表4 “陈述_v”框架语义角色标注任务上语料不同切分比例对模型性能指标的影响 图2 “陈述_v”语义角色标注模型性能指标的信噪比 切分比例ΔP/%Stdev ΔP信噪比ΔR/%Stdev ΔR信噪比ΔF1/%Stdev ΔF1信噪比5∶511.830.011 410.364 9.950.008 911.22910.810.008 912.161 6∶411.710.012 39.472 10.400.011 39.186 11.020.010 310.656 7∶311.350.012 78.952 10.710.012 6948.437 11.050.011 19.914 8∶211.360.016 86.776 11.140.015 47.246 11.290.014 47.821 9∶111.570.025 04.636 11.600.025 34.578 11.650.023 25.020 综上可知: 随着切分比例的差异增大,标准差逐渐增加,信噪比逐渐变小,在5∶5切分时标准差达到最小,信噪比达到最大。也就是说,从信噪比角度来看,按照5∶5切分语料,更适用于文本数据的模型比较任务。 本节按5∶5切分的2折交叉验证,分析训练集、验证集的分布差异对指标的信噪比的影响。 本节主要基于语义角色标注任务,选取了例句数最多的6个框架(表6)作为研究对象,进行对比试验。首先,对每个框架的例句随机进行2折交叉验证,重复1 000次。然后,统计训练集、验证集上的词元分布频次及不同类型的语义角色的分布频次。根据式(4)所给的卡方统计量,分别计算词元及语义角色在训练集与验证集上的分布差异。 表6 各框架的语义角色标注模型性能指标的信噪比 表6给出了实验所用的6个汉语框架的基本信息,包括每个框架的句子数、词元个数及语义角色种类数,以及正则化条件中的正则化参数值c1和c2。在表6的后6列,分别给出了“正则化切分”以及“不好的切分”下,模型准确率、召回率和F1值的信噪比。 从表6可知,除“感受”框架的准确率外,“不好的切分”对应的准确率、召回率和F1值的信噪比均比“正则化切分”下对应的信噪比小。这说明词元分布差异和角色类型分布差异的约束对指标的信噪比有明显的影响。也就是说,若采用了不好的切分,指标的信噪比会下降,容易导致不可靠的模型比较结论。 本节主要比较正则化m×2 交叉验证(m×2 BCV)下与随机m×2交叉验证(m×2 RCV)下各指标的信噪比。不失一般性,这里设置m为3。本节主要基于语义角色标注任务,以“陈述_v”为例进行分析。具体地,将“陈述”框架动词词元的所有例句作为语料,分别构造3×2 BCV以及3×2 RCV。对于每一种交叉验证,执行500次随机切分,并基于500次的实验结果计算模型各性能指标的均值、标准差及信噪比。构造3×2 RCV时,只需将整个按5∶5切分,随机切分三次。构造3×2 BCV的方式如下: 对于3×2 BCV,将语料均分为4份,将“陈述_v”框架的84个词元按其数量均匀分配到4份数据中,任取两份合起来作训练集,剩余两份作验证集,这样就可以得到3组2折交叉验证方案,并分别引入下面的正则化条件: 表7给出了“陈述_v”语义角色标注模型上3×2 BCV和3×2 RCV上的实验结果。从表7可见,3×2 BCV对应的准确率、召回率和F1值的标准差均有所降低。另外,3×2 BCV下的信噪比均大于3×2 RCV下的信噪比,说明引入正则化条件后的3×2 BCV能够改善指标估计,有利于得到更为可靠的模型比较结论。 为了进一步说明正则化条件的作用,我们从3×2 RCV的500次切分中,挑选出10次“不好的切分”(c1,c2≥1.055)。然后,从3×2 BCV的500次切分中,挑选出10次“较好的切分”(c1,c2≤0.35)。针对选出的切分,分别计算模型性能的各项指标。结果在表8中给出。 表8的结果表明,根据正则化条件所选出的3×2 BCV切分方案明显比3×2 RCV中“不好的切分”对应的F1值的信噪比高出许多。 表7 “陈述_v”语义角色标注模型上3×2 RCV与3×2 BCV的比较(500次切分) 表8 “陈述_v”框架词元分布的差异对指标的信噪比的影响(10次切分) 综上,基于5∶5的切分比例,通过合理地引入正则化条件,使用正则化的m×2 BCV后,模型性能指标的信噪比有明显改善。 基于交叉验证的模型比较是统计机器学习中的常用方法。本文针对文本数据的特点,研究了如何切分数据来构建合理的交叉验证方案,得到如下几点结论: 第一,文本数据的切分比例应当采用5∶5,即二折交叉验证,其他比例的切分都会增大指标估计的方差,降低指标的信噪比。 第二,卡方统计量可用来度量数据切分导致的训练集和验证集的预测标记分布差异,并可用于构造数据切分的正则化条件。 第三,在构建多个二折交叉验证(m×2 CV)时,应当以最大化信噪比为目标,采用正则化的数据切分(m×2 BCV)。本文以汉语框架语义角色标注为例,说明了如何设置正则化条件,及如何构造正则化的m×2 BCV。实验结果也验证了该方法的有效性。 传统的将数据简单切分为训练集、验证集、测试集的方法,在数据量较大时才较为有效。对文本数据,当数据量较大时,计算开销也非常大。此时,要得到方差的估计是困难的,进而导致后续的统计显著性检验及统计推断任务无法进行。我们认为,在模型初选时,应避免使用很大的数据集。一条可行思路是: 首先选取适当大小的数据,并借助正则化的m×2 BCV对数据进行有效利用,选出有效的特征,甄别出优良的模型。当确定出较好的模型后,再使用较大的数据,获得该模型的参数估计。本文的目标在于: 对于给定的文本数据,给出一种有效使用交叉验证的建模方法。文中所提到的正则化条件是文本数据切分时的最基本的约束条件,读者可以根据自然语言的具体任务,根据实验者的经验来设置正则化条件。不过,当多个正则化条件并存时,如何构建高效的切分仍然是后续需要研究的问题。此外,除卡方统计量外,采用其他差异度量,比如相似度等是否更为有效,也是下一步需要研究的问题。
6 实验
6.1 切分比例对模型性能指标估计的影响


6.2 训练集与验证集的分布差异对模型性能指标估计的影响

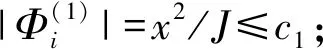
6.3 比较正则化m×2交叉验证和随机m×2交叉验证方法
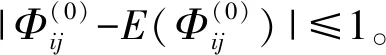




7 结论与展望

