离合器最优控制权系数变化对车辆性能的影响*

金 辉，于 倩

（北京理工大学智能车辆研究所，北京 100081）

前言

离合器的接合控制一直是AMT车辆起步和换挡过程中的关键问题。AMT车辆对离合器的控制会影响驾驶性能，包括起步性能、换挡质量、车辆可靠性和安全性等［1］。同时，对离合器的控制研究，在提升混合动力汽车工作模式的切换性能［2］和双离合器车辆的工作性能方面也有着重要的意义。

由于AMT起步时的离合器控制问题是多目标控制问题，所以采用多目标约束下的代价函数最小为目标的最优控制策略，理论上更加适合AMT车辆的起步控制［3］。文献［4］中对模型预测控制和线性二次型控制（linear quadratic regulator，LQR）两种算法进行了对比：指出模型预测控制对模型的变化和扰动比较敏感，进而会导致控制算法失效；相比之下，线性二次型控制对模型变化的适应性更强。文献［5］和文献［6］中通过分析驾驶员起步意图得到了最优控制中性能函数的不同惩罚系数，但是并没有系统、理论地解释权系数的取值依据，且仅列举了3种权系数取值，没有进一步研究权系数动态变化对车辆性能的影响。重庆大学陈清洪等将发动机转速和离合器输出转速作为状态变量，在冲击度满足乘坐舒适性的前提下以滑摩功最小为优化目标，将冲击度转化为最优控制的约束条件，避免了多目标优化中权系数选择的难点［7］。上海交通大学戴丰用隐马尔可夫模型对不同起步意图进行建模与识别，以量化的冲击度为输出，将驾驶员起步意图和离合器最优控制过程结合到一起［8］。但是文献［7］和文献［8］中的两种策略仅仅满足了对冲击度的需求，没有进一步研究车辆其它起步性能随权系数变化的情况，比如发动机需求转矩以及滑摩功等。

本文中针对AMT车辆起步过程中的离合器控制，利用最优控制理论设计了线性二次型调节器，通过层次分析法，根据两种极端驾驶员风格确定了各权系数的边界值，通过大量仿真实验得到各个权系数变化时冲击度、滑摩功、滑摩时间和发动机需求转矩随之变化的情况。

1 离合器接合过程建模

1.1 传动系降阶模型

典型的AMT传动系统包括如下几个部分：发动机、干式离合器、变速器、减速器和驱动轮。本文中建立的是整车纵向动力学模型，因此对离合器系统进行简化处理，得到的简化降阶传动系物理模型如图1所示。

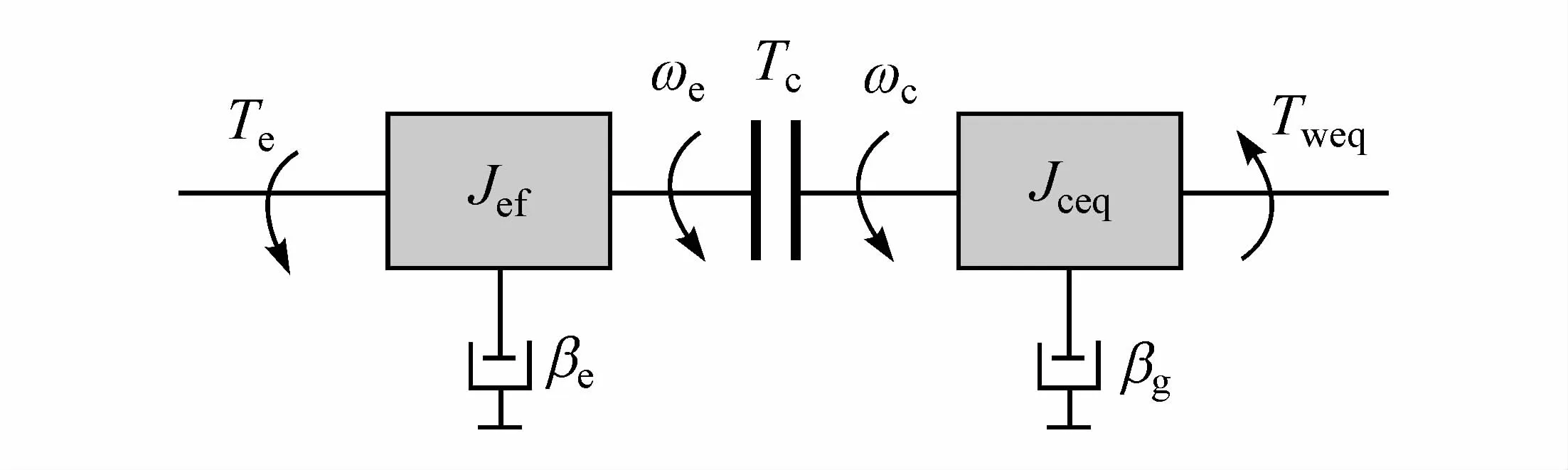
图1 AMT车辆离合器系统降阶模型

图中，βe和βg分别为发动机曲轴和变速器输入轴旋转黏滞阻尼系数，Jef和Jceq分别为发动机曲轴、飞轮盘的总等效转动惯量和离合器从动盘处的总等效转动惯量，Te和ωe分别为发动机输出转矩和发动机角速度，Tc和ωc分别为离合器传递的转矩和离合器从动部分的角速度，Tweq为等效到离合器从动盘的负载转矩。由图可知降阶传动系中动力学关系为

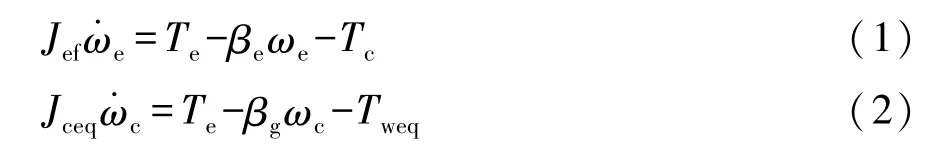
1.2 离合器模型

离合器滑摩时，摩擦片传递的转矩为

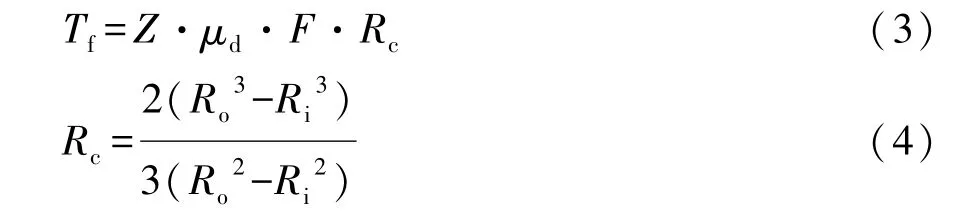
式中：Z为离合器摩擦副数；F为摩擦面的正压力；μd为摩擦因数；Rc为摩擦片的平均摩擦半径；Ro和Ri为摩擦片的外径与内径。

根据离合器分离轴承的位置x0和发动机转矩关系可得各阶段离合器传递转矩：

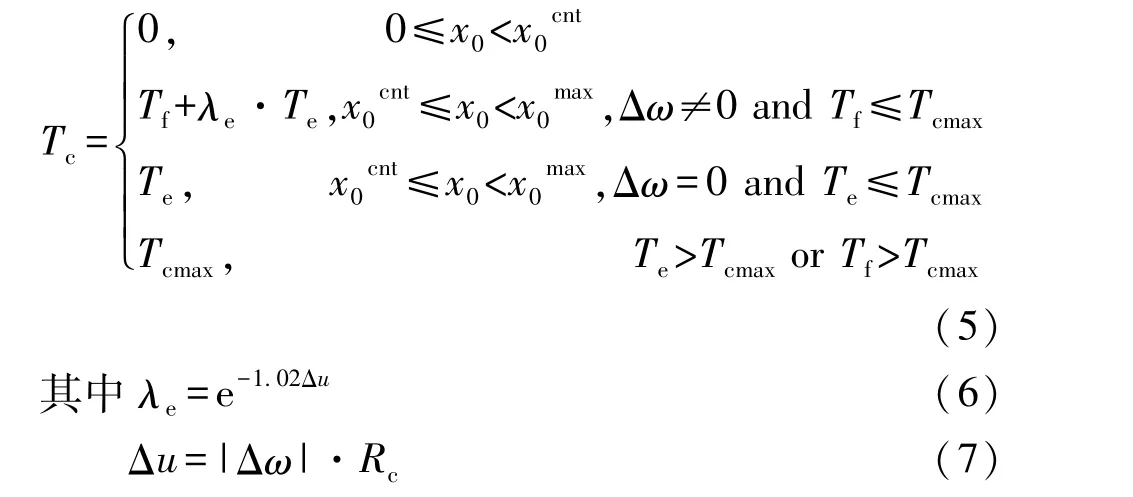
2 线性二次型调节器设计

2.1 LQR设计

根据起步性能指标，需减少起步过程中离合器滑摩接合阶段的滑摩功、滑摩时间以及冲击度。因此对于动力学方程式所表达的离合器滑摩接合阶段，可建立如下基于滑摩时间、滑摩功以及冲击度等性能指标的综合性能最优的二次型性能指标泛函式：

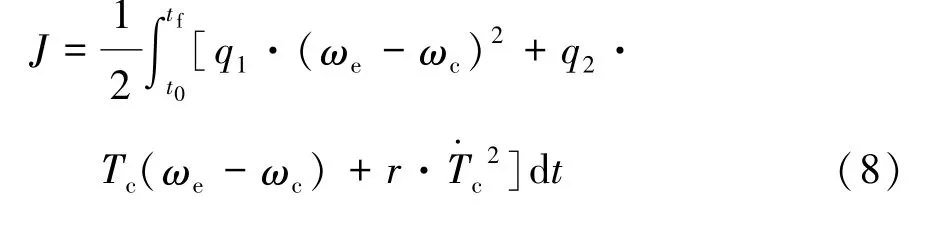
将相应的起步性能指标泛函式（8）表示为二次型性能指标形式：

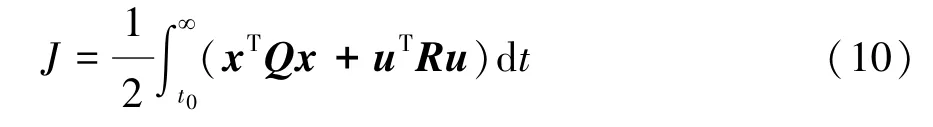
式中权系数矩阵Q，R应分别满足：

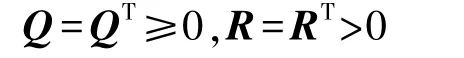
本文中权系数矩阵分别为

构造如下哈密顿函数：

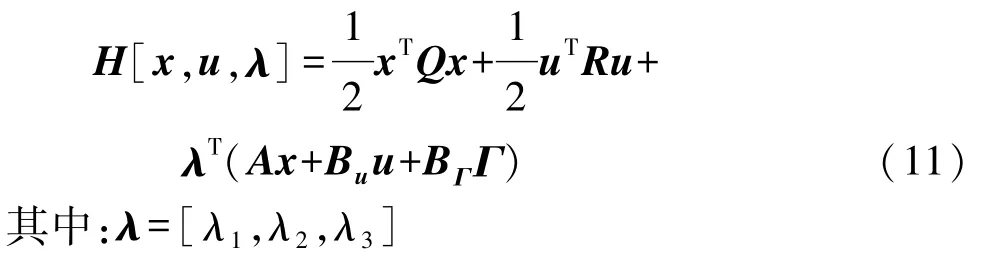
式中λ为待定的拉格朗日乘子向量。根据极小值原理：

由于系统扰动量Γ的存在，本文中设λ为系统状态量x和系统扰动量Γ的线性组合，即

代入式（15），可得系统的最优控制律为

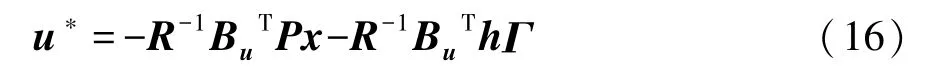
式中P和R为待定定值矩阵，P为满足代数Riccati方程PA-PBuR-1BuTP＋Q＋ATP=0的唯一解。R的确定过程如下。

根据汉密尔顿正则方程：

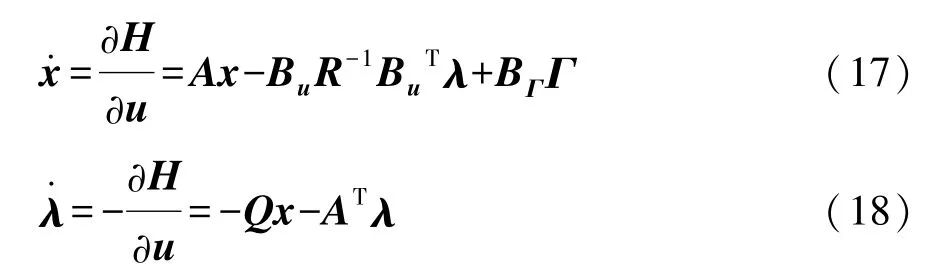
对式（12）求导，结合正则方程，得

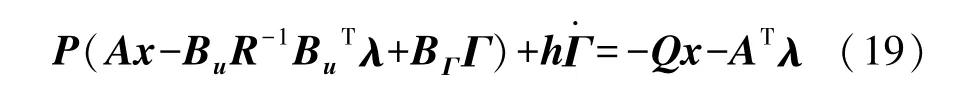
将λ代入式（16），并结合Riccati方程，得

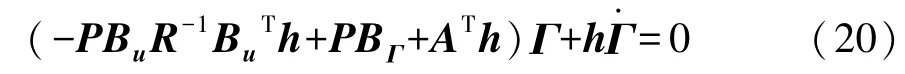
由于车辆起步阶段车速较低，所以可认为等效阻力矩基本恒定，即 Γ·=0，有

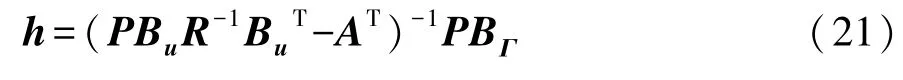
将P和R代入最优控制律u*，结合x和Γ的定义，控制策略最终简化为

其中：

2.2 权系数对起步性能的影响

根据2.1节中对线性二次型调节器最优解的求解过程可知，权系数矩阵Q和R是计算初始由设计者给出的某常数矩阵，q1，q2和 r分别影响滑摩时间、滑摩功以及冲击度在性能指标函数中的权重，所以本节中研究权系数变化对不同起步性能指标的影响。

首先确定权系数的边界值。在综合评价体系中，为体现不同评价指标对总体性能目标影响的大小及其重要程度，需对各指标进行合理的权重分配。本文中依据驾驶员风格对目标函数的权系数进行赋权，因为主观赋权法能较好地体现评价者的主观偏好，所以本文中采用主观赋权方法中的层次分析法，求解步骤如下。

（1）建立层次结构模型

本文中所研究的问题可以简化为一个单层结构模型，决策目标为起步综合性能评价指标，评价指标分别为滑摩时间、滑摩功和冲击度。

（2）构造各层次中的所有比较矩阵

本文中的单层结构模型采用的比较矩阵是一个3×3的矩阵A，定义A为

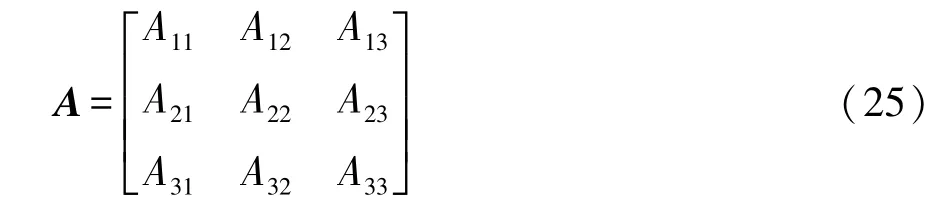
矩阵A的取值根据Saaty提出的9标度方法确定［9］，标度值 Aij由决策者通过比较Ai和 Aj后在自然数0～9间选定，Aij越大，表示 Ai相比于 Aj更重要。倒数表示两个指标相比时，后者相比于前者的重要性标度值，即 Aii=1，Aji=1／Aij。

根据不同风格驾驶员的主观判断，判断矩阵也各不相同。

（a）风格激进驾驶员的判断矩阵选择

对于风格极端激进的驾驶员而言，起步时间相比于冲击度而言极端重要（标度值为9），起步时间相比于滑摩功而言明显重要（标度值为5），而滑摩功相比于冲击度而言稍稍重要（标度值为3）。则判断矩阵为

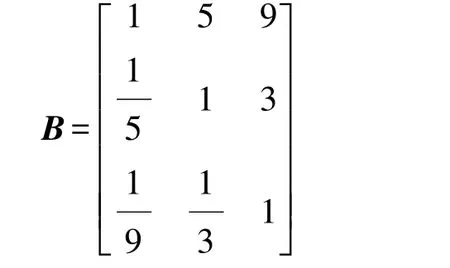
该判断矩阵的最大特征值为λmax=3.0291，对应的归一化特征向量（即权系数分配）为

［0.751 4 0.178 2 0.070 4］

（b）风格稳健驾驶员的判断矩阵选择

对于风格极端稳健的驾驶员而言，冲击度相比于起步时间而言极端重要（标度值为9），冲击度相比于滑摩功而言强烈重要（标度值为7），而滑摩功相比于起步时间稍稍重要（标度值为3）。则判断矩阵为

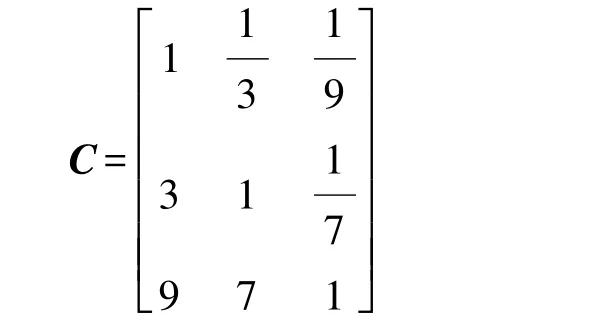
该判断矩阵的最大特征值λ′max=3.0803，对应归一化特征向量（即权系数分配）为

［0.068 5 0.148 8 0.785 4］

（3）一致性检验

当判断矩阵的阶数大于2时，构造出的矩阵很可能并非一致性矩阵，但只要保证在一定的偏离范围内就认为其满足一致性要求，检验步骤如下。

（a）计算一致性指标

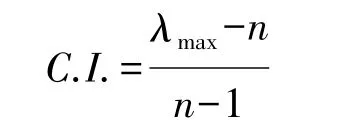
式中n为矩阵A的秩。

（b）计算平均随机一致性指标R．I．

R．I．是多次重复进行随机判断矩阵特征值的计算后取算数平均数得到，可由平均随机一致性指标标准值查表获得。

（c）计算一致性比例

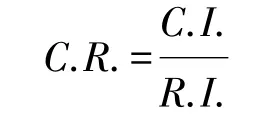
当C．R．＜0.1时，通常可认为该判断矩阵符合一致性要求。

对上述判断矩阵进行一致性检验，可知两种情况下的判断矩阵都可以接受。

3 仿真实验研究

将2.2节中解得的两种极端风格对应的权系数作为边界值，采用控制变量法，分别研究某一个权系数变化时，发动机输出转矩和离合器传递转矩、起步过程中冲击度和滑摩功随之变化的规律。在本文中，为简化计算过程，当研究某一权系数时，令其它两个权系数取相同值。通过大量仿真实验，确定了权系数的取值范围以及各权系数变化对车辆起步性能的影响情况，如图2～图4所示。图2（a）、图3（a）和图4（a）中上部分3条线是发动机输出转矩，下部分3条线是离合器传递的转矩。权系数变化时，车辆各个起步性能指标对应的数值及其变化率整理如表1所示。

分析可得如下结论：

（1）增大滑摩时间权系数q1值，有利于缩短离合器接合时间，提高起步的快速性，同时有利于减小滑摩功，但冲击度和发动机需求转矩均变大；

（2）增大滑摩功权系数q2值，有利于减少滑摩功和接合时间，车辆的起步快速性得以提高，但同时引起的滑摩冲击度和同步冲击度均有所增大，发动机需求转矩也有所提高；

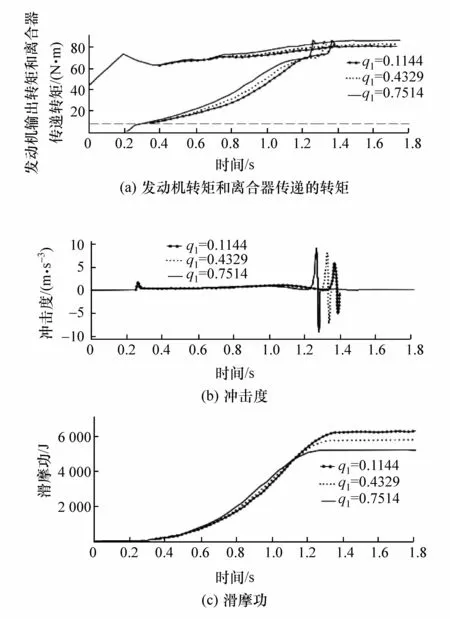
图2 滑摩时间权系数变化时车辆起步性能变化图

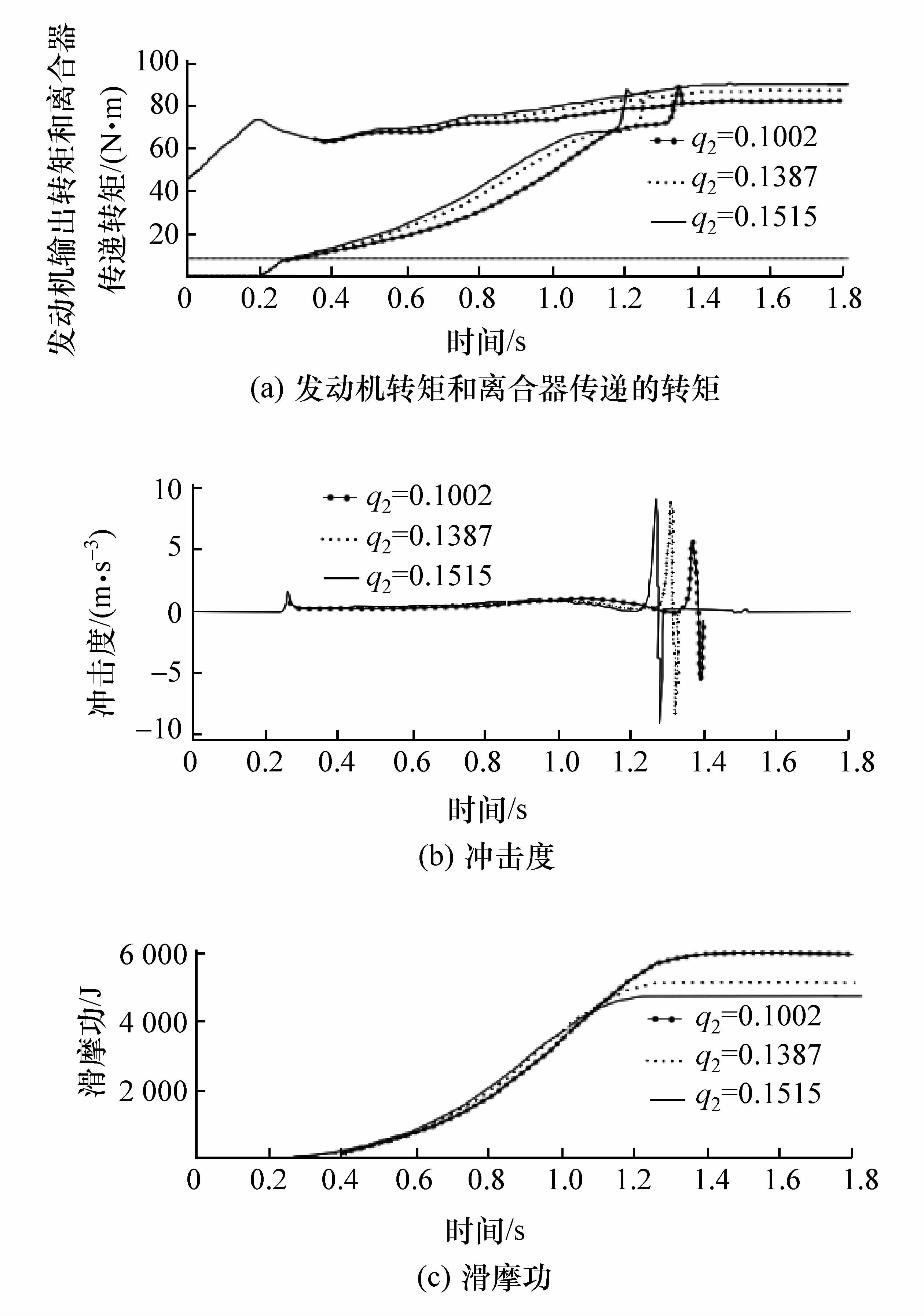
图3 滑摩功权系数变化时车辆起步性能变化图

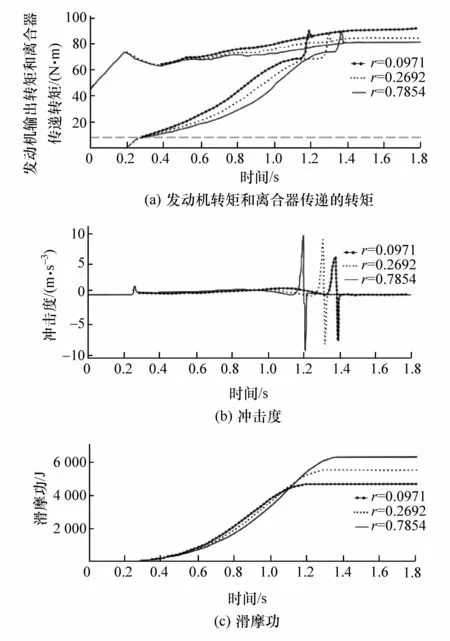
图4 冲击度权系数变化时车辆起步性能变化图

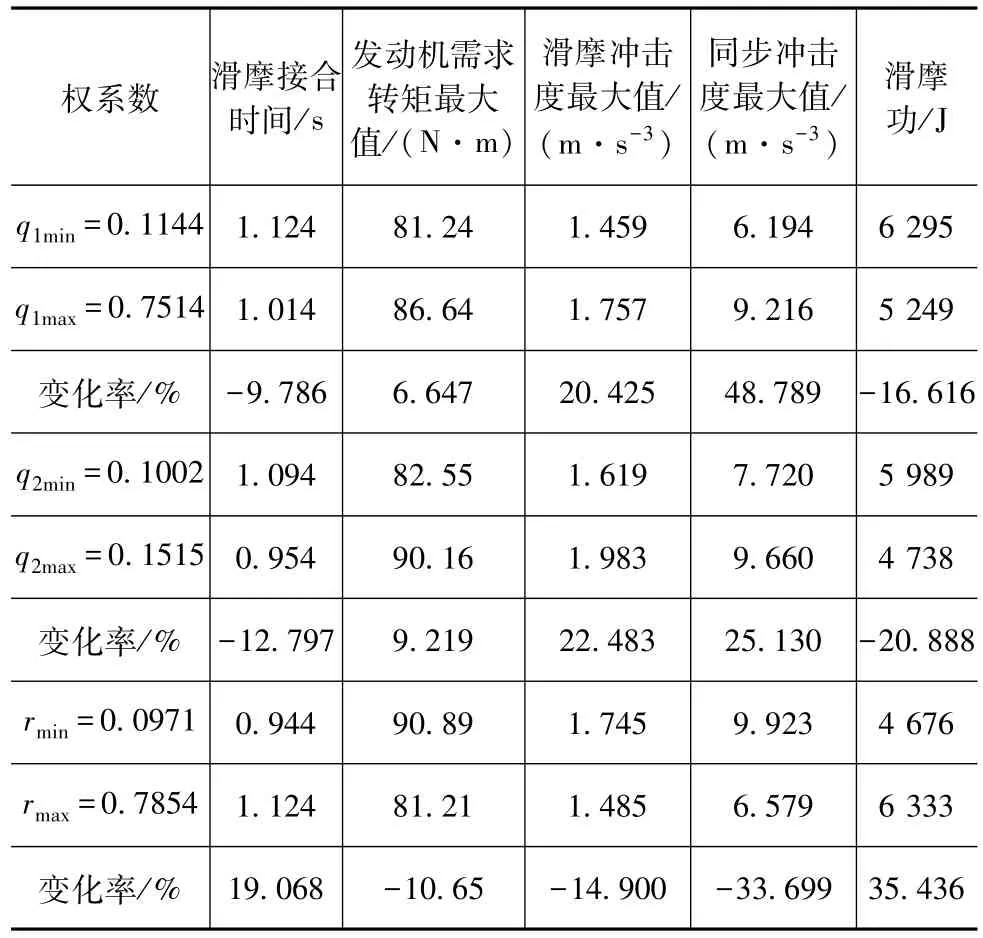
表1 权系数变化对车辆起步性能的影响

（3）增大车辆冲击度权系数r值，有利于降低冲击度，但离合器接合时间增大，起步过程变慢，同时滑摩功也将变大，但发动机需求转矩有所减小。

通过上述分析可知，为获得需求的车辆起步性能，各权系数可做相应的调整，其调整趋势如表2所示。其中，发动机转矩储备系数为发动机外特性曲线上的最大转矩与发动机需求转矩的比值，表示发动机转矩储备能力。储备系数越大，承载能力越强。

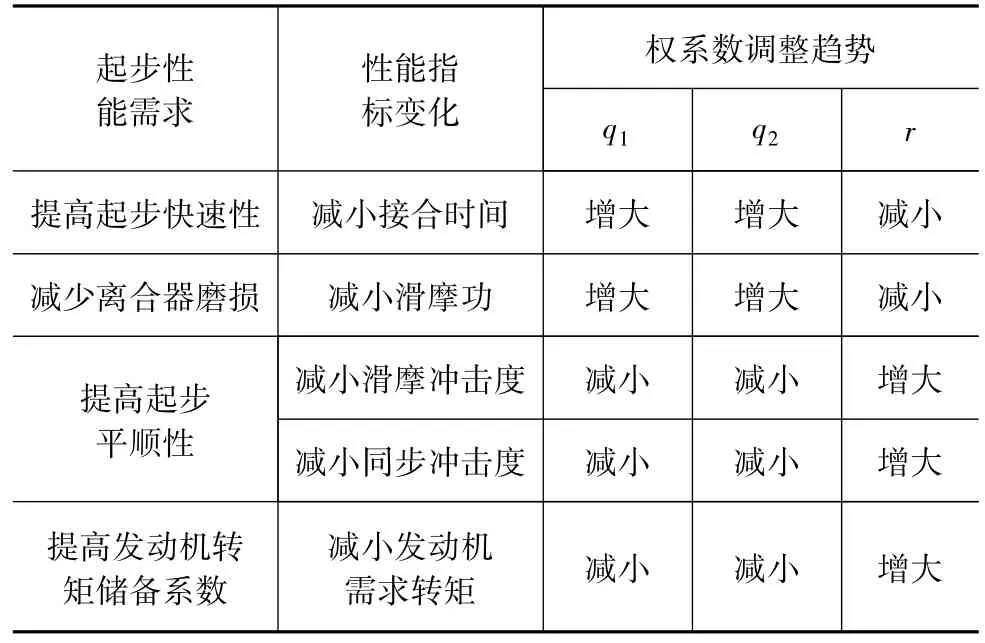
表2 车辆起步性能需求与权系数调整趋势关系

4 结论

本文中对离合器采用最优控制时权系数变化对车辆起步性能的影响进行了研究。通过层次分析法，根据极端驾驶员风格，对所设计的线性二次型调节器的权系数进行分配，确定了权系数的分配范围；并进行了大量仿真实验，分析实验结果可知：对于同一油门输入，权系数q1和q2越大，起步快速性越好，离合器磨损量越小，起步平顺性越差，发动机转矩储备系数越低；权系数r越大，起步平顺性越好，发动机转矩储备系数越高，起步快速性越差，离合器磨损量越大。起步快速性（即滑摩接合时间）与滑摩功大小之间始终呈现正相关，而与起步平顺性和发动机转矩储备系数之间始终相互制约。以上研究为对离合器进行驾驶员个性化控制打下了基础。