一种改进的加速度阻尼半主动控制策略研究*

郭孔辉，王 杨

（吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

独立悬架可分为麦弗逊、双横臂、多连杆等多种形式。弹性元件起承载作用，主要分为钢板弹簧、扭杆弹簧、螺旋弹簧和空气弹簧等。阻尼元件起减振作用，包括被动减振器和阻尼可调减振器，其中阻尼可调减振器包括电磁阀控阻尼可调减振器和电／磁流变液阻尼可调减振器等。根据阻尼或刚度调整范围和功耗的考虑，悬架也可分为阻尼自适应悬架、半主动悬架、慢主动悬架和全主动悬架等［1］。

综合考虑能耗、控制带宽和系统的稳定性等因素，半主动悬架能够在性能和成本等方面达到最好的折中。针对半主动悬架控制算法的研究受到国内外学者的广泛关注［2］，也提出了诸多控制算法，诸如基于参考模型的滑模控制［3-5］，鲁棒控制［6-7］和最优控制［8-10］等。在算法实时性、简便性和工程实现等方面，其中以Karnopp等最早提出天棚控制策略（skyhook control，SH）最为著名［11］。目前天棚控制是研究和工程应用最广泛的半主动控制策略之一。Sammier等提出了改进的线性天棚控制，能够根据车身振动速度线性调节阻尼范围［12］。Savaresi等提出了加速度阻尼控制（acceleration driven damper，ADD）［13］，并利用最优控制理论证明了其有效性。Morselli等利用端口哈密顿方法提出了PDD（power driven damper control）控制方法［14］。

Savaresi等对比分析了开关型的SH和ADD的优缺点［15］，即SH在低频段（车身振动偏频附近）效果明显，而在高频段（车身振动偏频以上）效果不明显甚至恶化；ADD的控制特性是在低频段控制效果不明显，但在高频段却能够很好地抑制振动，控制效果较好。基于此Savaresi等提出了Mixed SH-ADD算法，能够结合SH和ADD控制优点，实现全频域内降低车辆振动加速度，虽然Savaresi指出SH和ADD在控制性能中的优缺点，但是并没有说明其原因，Mixed SH-ADD算法具有较好的控制效果，但是其提出的频率选择器由于自身的特性不能够在分频点附近实现完全分频。Liu等提出了Mixed SH-PDD控制算法，同样也利用一种分频函数，在低频时采用SH控制，高频时采用PDD控制，这样该算法不仅在整个激励频域内降低振动加速度，同时减低振颤，并利用能量流进行算法分析［16］。

针对诸如油气悬架等刚度和阻尼能够同时调节的系统，Spelta等提出结合Mix SH-ADD和悬架动行程门限逻辑控制的算法，能够更进一步提高乘坐舒适性［17-18］。Dande在论文中阐述了SH和ADD控制在相频特性的差别，提出一种基于规则的控制算法［19］。

基于以上原因，本文中首先深入分析SH和ADD的控制特性，并从相频的角度对其进行理论分析，然后提出了改进的ADD控制策略，能够实现在全频域内的降低车辆的振动加速度，该改进的ADD是面向乘坐舒适性的半主动控制策略。

1 SH和ADD分析

图1为2自由度的车辆振动模型，下面对其进行动力学建模［1］。

建立动力学方程：

图1 2自由度车辆振动模型

式中：M为簧上质量；m为簧下质量；z为簧上质量垂向位移；zt为簧下质量垂向位移；zr为路面激励；k为悬架刚度；c为悬架阻尼系数；kt为轮胎刚度。

1.1 SH控制特性分析

在SH控制中，假设存在一个阻尼器连接在参考位置（天空）和车身上，以抑制由于路面不平度激励引起的车身振动，对于开关型的SH控制，有

为分析SH的控制逻辑的

相频特性，车身速度与悬架运动相对速度的传递函数关系为

所以相频特性如图2所示。通过图2可知：在低频时，车身速度与悬架运动相对速度相位相同，没有相位差；在高频时，车身速度与悬架相对速度有90°的相位差。这表明：在低频区，SH控制逻辑能够按照控制逻辑执行控制算法，并抑制车辆的振动加速度；当路面的激励为高频激励时，则导致SH控制逻辑在执行时，不能完全按照控制逻辑执行。

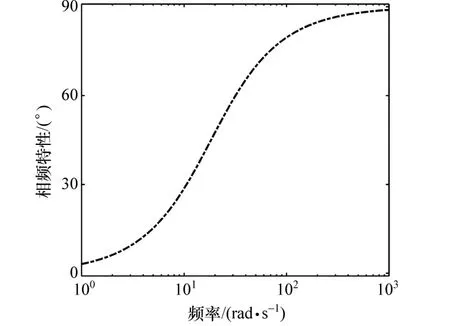
图2 SH控制逻辑相频特性

1.2 ADD控制特性分析

在汽车振动中，ADD控制以抑制车身加速度z··为目标，对于开关型的ADD控制，则有

为分析ADD控制逻辑的相频特性，车身加速度与悬架运动相对速度的传递函数关系为

所以相频特性如图3所示。通过图3可知：在低频时，车身加速度与悬架运动相对速度存在90°的相位差；在高频时，车身加速度与悬架运动相对速度有180°的相位差。这表明：在低频区，ADD控制不能完全按照控制逻辑执行；当路面的激励为高频激励时，在执行ADD控制逻辑时，恰好是以抑制惯性力为目标的控制逻辑，能够很好地抑制此频段的振动加速度。

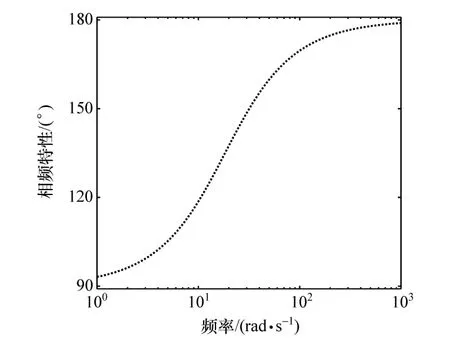
图3 ADD控制逻辑相频特性

通过对SH和ADD控制的相频特性分析，根据SH和ADD在不同频率段的控制特性，提出一种能够结合SH和ADD优点的改进ADD控制，实现全频域内的降低车辆振动加速度的目的。

2 改进 ADD控制［20］

通过对SH和ADD的控制特性分析，设计一个控制系统W，以车身加速度z··信号为控制系统输入，在低频时该控制系统为一个积分环节，能够将加速度信号z··变成速度信号z·；在高频时该控制系统近似为比例系数是1的比例环节，输出为加速度信号z··，最后将控制系统W输出的信号定义为S，如图4所示。

图4 控制算法简图

改进ADD控制可以表示为

式（7）的幅值和相位角分别为

式（8）和式（9）的Bode图如图5所示。

通过图5可知，在低频时，控制系统W能够在低频激励时给控制策略提供-90°的相角补偿，这可以改进原有ADD控制策略在低频时的控制特性的不足，因此将该方法命名为改进的ADD控制。

改进的ADD控制策略中判断逻辑的传递函数为

利用上式可以绘制相频特性，见图6。

通过图6可见：在低频时，提出的改进ADD控制策略具有与SH控制相近的相频特性；在高频时，改进的ADD控制具有与ADD控制一致的相频特性。也是基于此原因，提出的改进ADD控制能够结合SH和ADD控制的优点，具有全频域内提高乘坐舒适性的特性。

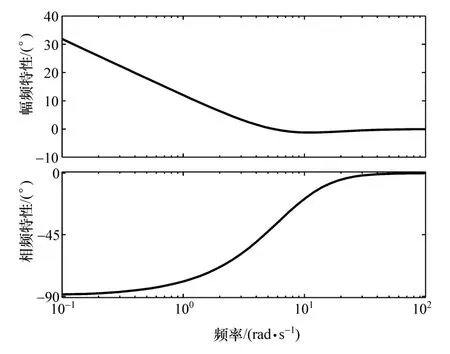
图5 控制系统W幅频与相频特性

图6 3种算法控制逻辑的相频特性

3 仿真分析

3.1 减振器响应时间模型

SH，ADD和改进的ADD控制策略为开关型控制，在阻尼力切换时存在“振颤”，而在实际的应用中，减振器的阻尼力响应时间会抑制“振颤”。用1阶惯性系统描述阻尼力响应特性：

式中β为减振器的响应带宽。

3.2 仿真分析

为验证对SH和ADD控制特性分析的正确性和改进ADD控制算法的有效性，利用1／4车辆模型进行仿真验证，模型参数如表1所示。

下面分别以不同频率的正弦波（1.25，4和12 Hz）作为激励，进行仿真分析。

表1 车辆模型参数

图7为分别以1.25，4和12 Hz的正弦波作为激励信号，验证提出的改进ADD算法在不同频率内的控制效果。图8为以正弦波扫频信号作为激励获得的幅频特性。通过图7和图8看出，在低频激励时，改进的ADD控制与SH控制特性一致，在高频时，改进的ADD控制与ADD控制的特性一致，所以本文中提出的改进ADD控制能够结合SH和ADD控制的优点，无论在低频区还是高频区控制效果都很好。

图7 3种控制策略在正弦波激励下的时域响应

4 试验验证

图8 正弦波扫频激励下的频域特性

4.1 可控减振器实物在环试验台搭建

为验证提出的改进ADD半主动控制算法，搭建可控减振器硬件在环试验台。基本原理为利用xPC Target实时系统，建立1／4车辆动力学模型，将车辆模型的悬架相对位移信息通过xPC Target经过标定处理后转换成控制信号给直线电机控制器，同时xPC Target的控制板卡采集力传感器信号，经过标定处理后转换成减振器阻尼力，返回给实时车辆动力学模型，由此构成硬件在环回路。同时通过xPC Target的控制板卡上的模拟信号输出引脚输出实时车辆的车身加速度信号和悬架运动相对速度信号。利用MotoHawk快速原型开发工具，将半主动控制算法（如SH）烧写到MotoHawk控制器中。其中，控制器输入是车身加速度信号和悬架相对速度信号，控制器输出是PWM控制信号，将PWM信号接到可控减振器的接线端子上，具体如图9所示。实物如图10所示。

图9 减振器硬件在环原理图

4.2 试验结果分析

图10 减振器硬件在环实物图

为验证半主动控制算法，采用车速为72 km／h的C级随机路面作为激励，试验时间为120 s，由于采用磁流变液减振器，被动悬架分别以最大阻尼和最小阻尼作为参考。图11和图12分别为在不同情况下车身振动加速度的时域图和频域图。

图11 随机路面下的时域图

图12 随机路面下的频域图

表2为不同控制策略下的加速度均方根值对比。可以看出，与最大／最小阻尼系数的被动悬架和SH及ADD控制相比，改进的ADD控制能够明显抑制车辆的振动加速度。

表2 不同控制策略下的加速度均方根值对比

5 结论

针对面向乘坐舒适性的半主动悬架控制策略，首先从相频的角度分析了开关型的SH控制和ADD控制的不足，从而提出了一种改进的ADD控制策略，能够在整个激励频域内都有较好的控制效果，并从相频角度给予证明。然后通过仿真，利用3种不同频率的正弦波信号作为激励分析不同频率的控制效果，同时利用正弦波扫频信号作为输入，验证了全频域内的控制效果。仿真表明所提出改进的ADD控制能够在整个激励频率范围内降低车辆的振动加速度。最后搭建一个可控减振器的硬件在环试验台，验证了控制算法的有效性，该算法实时性好，易于工程实现。