THE CHARACTERIZATION OF EFFICIENCY AND SADDLE POINT CRITERIA FOR MULTIOBJECTIVE OPTIMIZATION PROBLEM WITH VANISHING CONSTRAINTS∗
Anurag JAYSWAL Vivek SINGH
Department of Applied Mathematics,Indian Institute of Technology(Indian School of Mines),Dhanbad 826 004,Jharkhand,India E-mail:anurag@iitism.ac.in;viveksingh.25jun@gmail.com
Abstract In this article,we focus to study about modi fied objective function approach for multiobjective optimization problem with vanishing constraints.An equivalent η-approximated multiobjective optimization problem is constructed by a modi fication of the objective function in the original considered optimization problem.Furthermore,we discuss saddle point criteria for the aforesaid problem.Moreover,we present some examples to verify the established results.
Key words multiobjective optimization problem with vanishing constraints;efficient solution;invexity;η-Lagrange function;saddle point
1 Introduction
The importance of mathematical program with vanishing constraints is well known in optimization theory as they occur in large numbers of applications in optimal topology design of mechanical structure.Vanishing constraint usually violates standard constraint quali fications,which gives rise to serious difficulties in theoretical and numerical treatment of these problems.
Over the last decade,several authors have developed tools to solve a special class of optimization problems with vanishing constraints(OPVC)which is also known as the mathematical programming problems with vanishing constraints(MPVC)see[1,6–8,10].Such a type of an optimization problem was first introduced by Achtziger and Kanzow[1]which can be used as a uni fied frame work for several applications in structural and topology optimization.Also,he discussed closely relation between MPVC and a mathematical programming problem with equilibrium constraints(MPEC)see[4,9,11]for more details.
Subsequently in the topic of MPVC,Hoheisel and Kanzow[8]investigated the Abadie and Guignard constraint quali fications and showed that the Abadie constraint quali fications is too strong assumption for MPVC,while the Guignard constraint quali fication hold in many situations.Recently,various types of constraint quali fications for multiobjective optimization problem with vanishing constraints(MOPVC)were introduced by Mishra et al.[10].He discussed their relations and derived the KKT necessary optimality conditions for efficiency.
On the other hand,considerable attention was given to devising new methods which allow the characterization of solvability of the original multiobjective programming problem with the help of some associated vector optimization problem.In[2,3],Antczak applied a new modi fied objective function method to characterize solvability of di ff erentiable multiobjective optimization problems under invexity hypotheses.He established the equivalence between the weakly efficient solutions of the original problem and its modi fied objective function problem.Further,he de fined a vector-valued Lagrange function and used it to obtain saddle point optimality results.
Consequently,in the present work,we concentrate on studying the modi fied objective function approach for multiobjective optimization problem with vanishing constraints,by means of employing invex functions.Further,we de fine η-Lagrange function,saddle point for the η-Lagrangian and establish various saddle point results.
The summary of the paper is as follows.Section 2 contains basic de finitions and a few basic auxiliary results,which will be needed later in the sequel.Section 3 is devoted to the optimality conditions.Furthermore,in Section 4,we establish the relationship between a saddle point of the η-Lagrange function and an(weak)Pareto solution of the considered multiobjective optimization problem with vanishing constraints.The final Section 5 contains the concluding remarks and further developments.
2 Preliminaries
The following notations will be used in this paper.
Let us denote by Λnthe index set of the form Λn={1,···,n}.For any x=(x1,···,xn)T,y=(y1,···,yn)T,we de fine

The problem to be considered in the present analysis is the multiobjective optimization problem with inequality,equality and vanishing constraints of the form:

where all functions fi,gj,hk,Hα,Gα:X →R are assumed to be continuously di ff erentiable on a nonempty open set X⊂Rn.The region where the constraints are satis fied(feasibility region)is given by
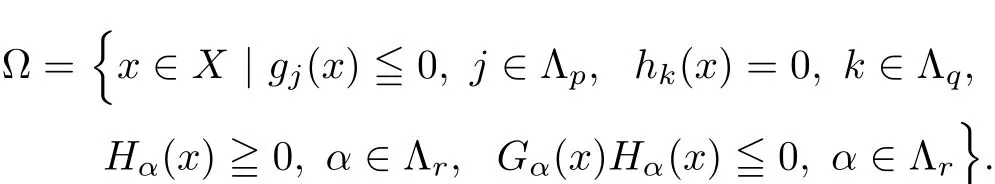
A multiobjective optimization problem,unlike single objective optimization problem does not necessarily have an optimal solution because all objective functions are in the con flicting nature.Therefore,there may not exists a single solution which optimizes all objective functions simultaneously.Thus,attention is paid to(weak)Pareto optimality[12];that is,solutions that cannot be improved in any of the objectives without degrading at least one of the other objectives.In this regard the concepts of(weak)Pareto optimality is widely used.
De finition 2.1A point x∗∈Ω is said to be an efficient solution(a Pareto solution)for(MOPVC)if and only if there is no x∈Ω such that

De finition 2.2A point x∗∈ Ω is said to be a weak efficient solution(a weak Pareto solution)for(MOPVC)if and only if there is no x∈Ω such that
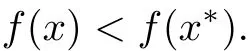
Let x∗∈Ω be an arbitrary feasible point.We de fine the following index sets

The index set Λr+can be further divided into the following subsets:
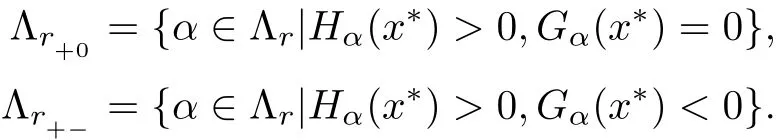
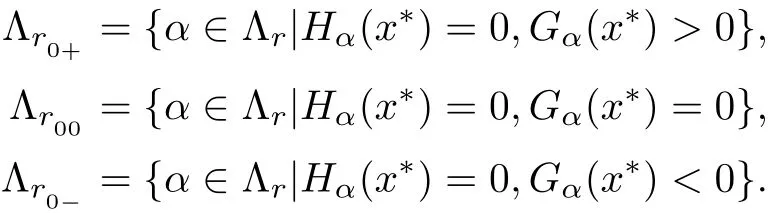
Now,we recall the de finitions of invexity and pseudoinvexity for a vectorial function introduced by Antczak[2].
De finition 2.3Let f:X→Rmbe di ff erentiable function on a nonempty open set X⊆Rn,and η:X×X→Rnbe a vector valued function.Then,we say that f is
(i)invex at the point y on X with respect to η if,for all x ∈ X,the following inequality

We also say that f is strictly invex at the point y on X with respect to η if the above inequality is strict and x 6=y;
(ii)pseudoinvex at the point y on X with respect to η if,for all x ∈ X,the following inequality

We also say that f is strictly pseudoinvex at the point y on X with respect to η if the above inequality is strict for all x∈X,x 6=y;
(iii) quasiinvex at the point y on X with respect to η if,for all x ∈ X,the following inequality

To prove various results in the paper,we are using the following necessary optimality conditions of Karush-Kuhn-Tucker type for such a multiobjective optimization problem with vanishing constraints,under the modi fied generalized Guignard constraint quali fication(GGCQMOPVC).
Theorem 2.4(see[10]) Let x∗∈ Ω be an(weak)efficient solution for(MOPVC)such that the GGCQ-MOPVC[10]holds at x∗.Then,there exist Langrange multipliers λi∈ R,i∈Λm,µj∈R,j∈Λp,ρk∈R,k∈Λq,,∈R,α∈Λr,such that the following conditions are satis fied

and
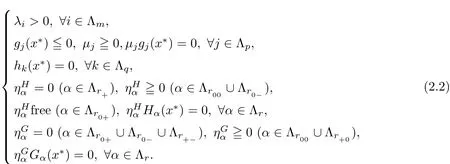
3 Modi fied Multiobjective Problem with Vanishing Constraints
Let x∗be a given feasible solution for(MOPVC).Then the modi fied multiobjective program with vanishing constraints corresponding to(MOPVC)is de fined as:

where all functions fi,gj,hk,Hα,Gα:X →R are de fined as in the problem(MOPVC).
Remark 3.1Note that Ω is also the feasible set of the modi fied objective function problem(MOPVCη(x∗)).
We de fine the following index sets
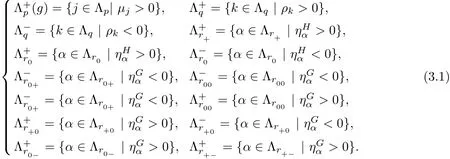
Theorem 3.2Let x∗∈Ω be an efficient solution of(MOPVC)and the GGCQ-MOPVC holds at x∗.Assume thatare invex at x∗on the feasible set Ω with respect to η and η(x∗,x∗)=0.Then,x∗is also an efficient solution of(MOPVCη(x∗)).
ProofSince x∗is an efficient solution for(MOPVC)and the GGCQ-MOPVC holds at x∗,then necessary opimality conditions(2.1)–(2.2)are satis fied.Assume to the contrary that x∗is an efficient solution of(MOPVCη(x∗)).Then,there exists feasible point∈Ω such that
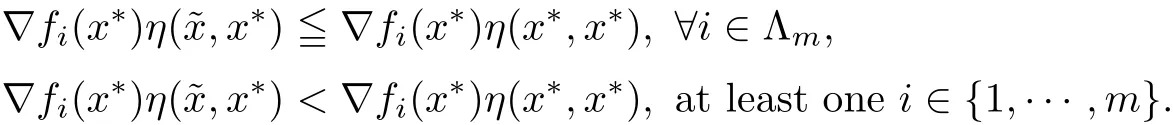
Since η(x∗,x∗)=0,therefore,the above inequalities reduce to

Multiplying each inequality(3.2)and(3.3)by λi>0,i∈ Λm,and then adding both sides of the obtained inequalities,we get
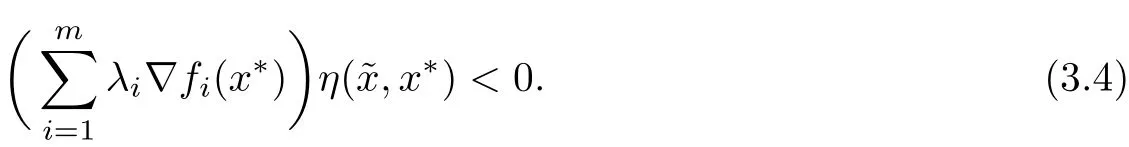
On utilizing the feasibility oftogether withwe arrive at
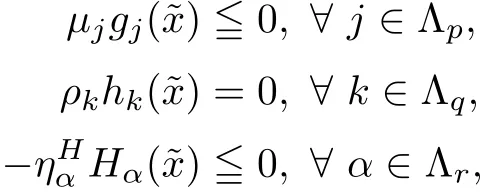
and
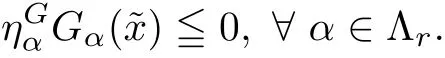
The above relations together with(2.2)gives


and

which by the de finition of index sets(3.1)yields

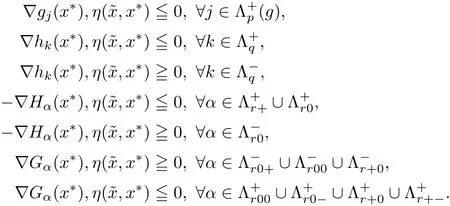
Again,by using(3.1),the above inequalities yields

On adding inequalities(3.4)and(3.5),we obtain

which contradicts(2.1).Hence,x∗is an efficient solution for(MOPVCη(x∗)).This completes the proof. ?
Now,we demonstrate the result established in Theorem 3.2 by the following example.
Example 3.3Let X={x=(x1,x2)∈ R2:−1 The feasible set of(MOPVC1)is given by.Clearly,x∗=(0,0)is an efficient point of the considered problems(MOPVC2).Let η:Ω×Ω→R2be de fined as It can be easily shown that the objective function f and the constraint function g1,h1,H1and G1are invex at x∗=(0,0)on Ω with respect to η given above.Now,using the approach discussed in the paper we construct the problem(MOPVC1η(x∗))by transforming the objective function.Thus,we obtain a linear multiobjective programming problem with vanishing constraints in the form: Since,all the hypothesis of Theorem 3.2 are ful filled,x∗=(0,0)is,therefore,an efficient solution of the modi fied multiobjective program with vanishing constraints(MOPVC1η(x∗)). Remark 3.4Note that the objective function is not convex at x∗=(0,0),which one can easily verify.Further,it is not difficult to see that the problem(MOPVC1η(x∗))constructed in the modi fied function method is convex.Hence,in some cases,we are in a position,by using the modi fied objective function method,to solve a nonconvex original problem(MOPVC1)by a convex one. In the next theorem,we prove the converse result to that one given in Theorem 3.2. Theorem 3.5Let x∗be a feasible point of(MOPVCη(x∗)).Assume that the objective functionare quasiinvex at x∗on Ω with respect to η and η(x∗,x∗)=0.If x∗is efficient solution for(MOPVCη(x∗)),then x∗is also an efficient solution of(MOPVC). ProofAssume to the contrary that x∗not be an efficient solution for(MOPVC).Then there exists a feasible pointsuch that By assumption,fi,i∈ Λmare quasiinvex at x∗on Ω with respect to η .Using De finition 2.3 together with(3.6),we obtain and also with(3.7),we get Combining(3.8)and(3.9)and using the hypothesis η(x∗,x∗)=0,we obtain which contradicts that x∗is efficient solution of(MOPVCη(x∗)).This completes the proof.? In this section,we establish an equivalence between an(weak)efficient solution of(MOPVC)and a saddle-point of(MOPVCη(x∗))under invexity assumptions. Now,we de fine the concept of an Lagrange function for a multiobjective programming problem with vanishing constraints(MOPVCη(x∗))as follows on the lines of Antczak[2]. De finition 4.1The Lagrange function(also called η-Lagrange function)is de fined by For a Lagrange function,some kinds of saddle points have been introduced,such as those in[13].Here,in the natural way,we give a de finition of a saddle point for the introduced Lagrange function in the multiobjective programming problem with vanishing constraints(MOPVCη(x∗)). De finition 4.2A pointis said to be a saddle point for the Lagrange function if Theorem 4.3Let x∗be a feasible solution of(MOPVC).Assume that the objective functionare pseudoinvex at x∗on Ω with respect to η satisfying the following condition η(x∗,x∗)=0.If(x∗,µ∗,ρ∗,η∗H,η∗G)is a saddle point of(MOPVCη(x∗)),then x∗is an(weak)efficient solution of(MOPVC). ProofSince(x∗,µ∗,ρ∗,η∗H,η∗G)is a saddle point of(MOPVCη(x∗)),by the de finition of a saddle point,we have which by the de finition of Lagrange function Since η(x∗,x∗)=0,the above relation gives that following inequality If we set(µ,ρ,ηH,ηG)=(0,0,0,0)in the inequality above,then we get Now,assume to the contrary that x∗is not a weak efficient solution for(MOPVC).Then,there exists a pointsuch that for all i=1,···,m By assumption fi,i ∈ Λmare pseudoinvex at x∗on Ω with respect to η,the inequality above implies Since x∗∈ Ω and,therefore,we have which implies that From(4.2)and(4.4),it follows that Combining(4.3)and(4.5),we get Thus,by the de finition of the Lagrange function,it follows that which contradicts the fact that(x∗,µ∗,ρ∗,η∗H,η∗G)is a saddle point of (MOPVCη(x∗)).Hence,x∗is a weak efficient solution of(MOPVC).This completes the proof. ? Now,we demonstrate the result established in Theorem 4.3 by the following example. Example 4.4Let X={x=(x1,x2)∈ R2:−1 The feasible set of(MOPVC2)is given by.Clearly,x∗=(0,0)is an efficient point of the considered problems(MOPVC2).Let η:Ω×Ω → R2be de fined as It can be easily shown that f is pseudoinvex at x∗=(0,0)on Ω with respect to η given above.Now,using the approach discussed in the paper we construct the problem(MOPVC2η(x∗))by transforming at x∗the objective function f.Thus,we obtain a linear multiobjective programming problem with vanishing constraints in the form: It is not difficult to see,that similar to the original(MOPVC2),x∗=(0,0)is also efficient solution in the above optimization problem with vanishing constraints which is constructed by a modi fication of the objective function in the original problem.The Lagrange function Lηin the problem(MOPVC2η(x∗))is given by We observe that(x∗,µ∗,ρ∗,η∗H,η∗G)=((0,0),1,0,1,0)is a saddle point,since and Since all hypotheses of Theorem 4.3 are ful filled,x∗=(0,0)is,therefore,an efficient solution in the consider multiobjectie programming problem with vanishing constraints(MOPVC2). Now,we prove the converse result,that is,a sufficient condition for a pointto be a saddle point for the η-Lagrange function. Theorem 4.5Let x∗be a(weak)efficient solution for(MOPVC)at which the GGCQMOPVC is satis fied.Assume thatare invex at x∗on Ω with respect to η and η(x∗,x∗)=0.Then,there existssuch that(x∗,µ∗,ρ∗,η∗H,η∗G)is a saddle point of the Lagrange function for(MOPVCη(x∗)). ProofSince x∗is an efficient solution for(MOPVC)at which the GGCQ-MOPVC is satis fied.Then by Theorem 2.4,conditions(2.1)and(2.2)are satis fied.Without losing generality,we assume.Sinceare invex with respect to η at x∗on Ω,then using(3.1),we see that which implies that The above inequality along with(2.1)implies By assumption η(x∗,x∗)=0,it follows that that is, On the other hand,from the feasibility of x∗∈Ω for(MOPVC)and using(2.2),we have which implies that Again,by assumption η(x∗,x∗)=0,it follows that By the de finition of the Lagrange function,we arrive at Thus,by inequalities(4.6)and(4.7),we conclude that(x∗,µ∗,ρ∗,η∗H,η∗G)is a saddle point for the Lagrange function for(MOPVCη(x∗)). ? In this paper,we have derived the optimality conditions for a multiobjective optimization problem with vanishing constraints involving invex and/or generalized invex functions by considering its associated vector optimization problem with the modi fied objective function.We also studied the saddle point criteria for the modi fied objective function problem.Hence,we observe that,under certain assumptions,this approach is useful from a practical point of view to determine an(weakly)efficient solution of a complex nonconvex problem as it is reduced to a much simpler form by modifying its objective function.Further,some examples of nonconvex problems have been presented to illustrate the results established in the paper.As it follows even from these examples,in some cases,problems constructed in the modi fied objective function approach for original nonconvex problems are convex or even linear.This means that we are in a position to solve nonconvex problems by the help of convex(or linear)ones.These results can be further extended to other classes of nonconvex multiobjective optimization problem with vanishing constraints and the methods to choose η in such a way that the original complex problems become easier,which will orient the future work of the authors.



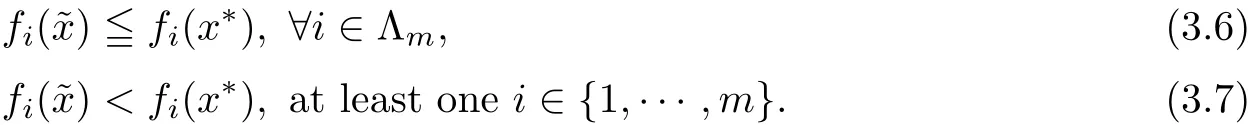



4 Saddle Point Criteria





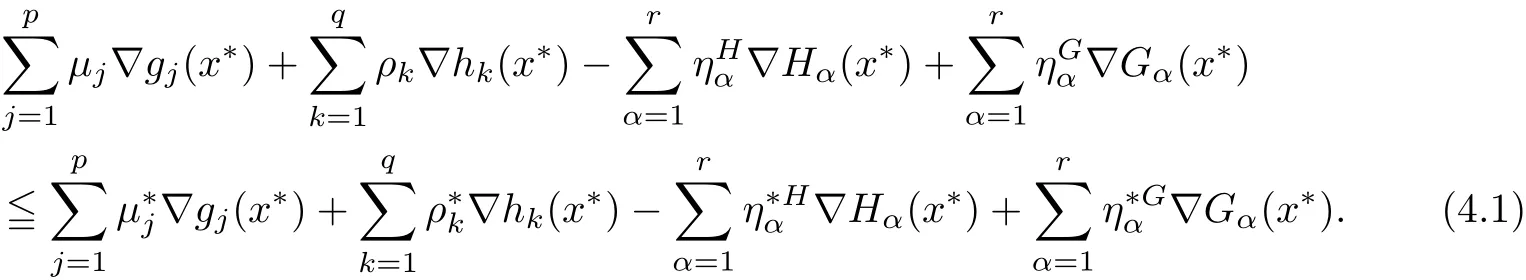

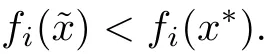

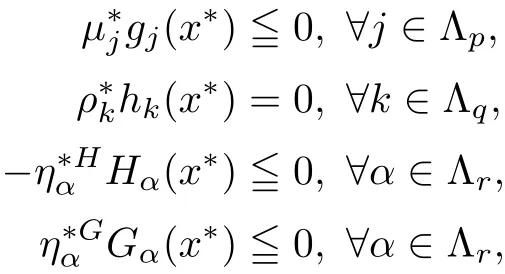







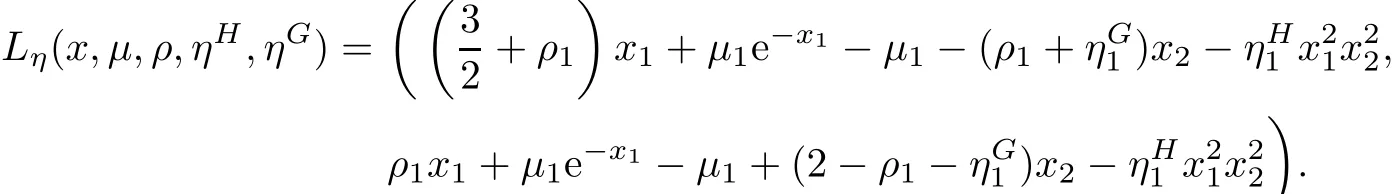
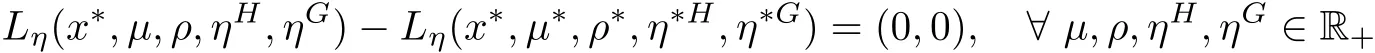

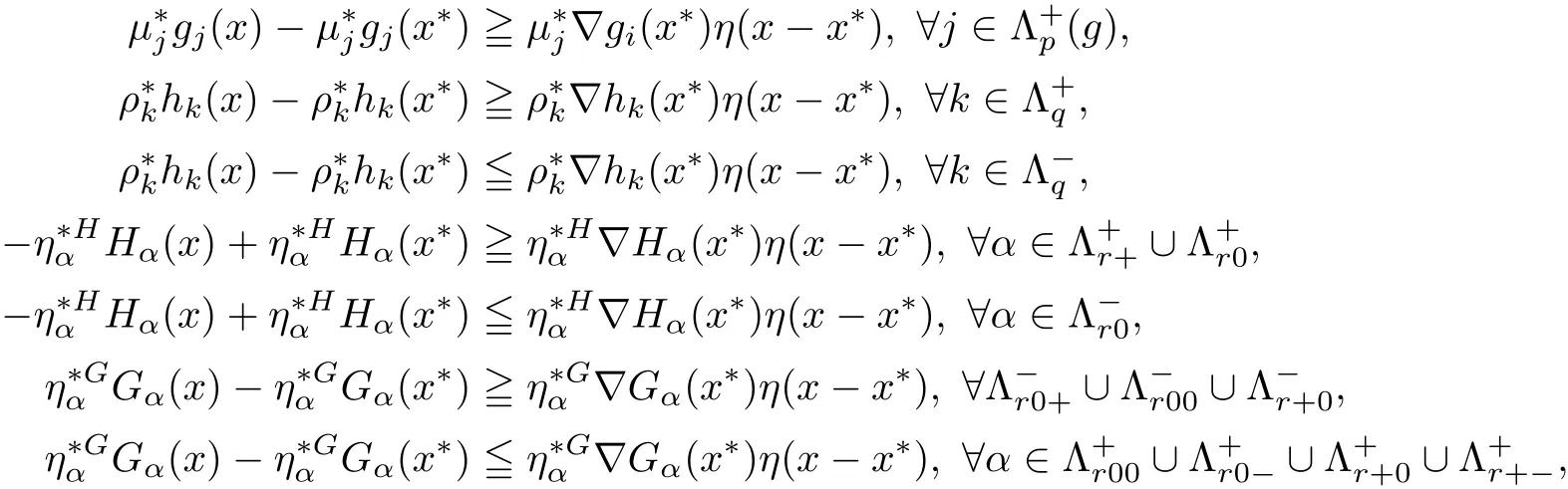


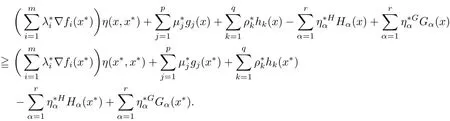



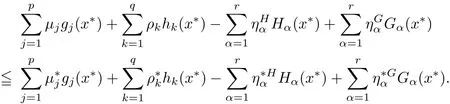
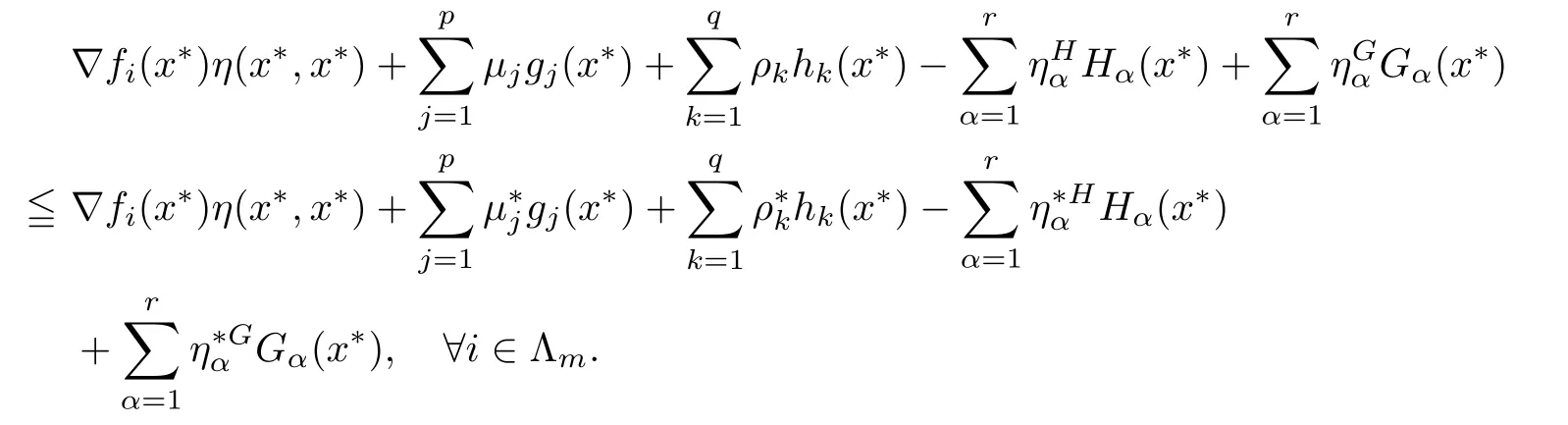
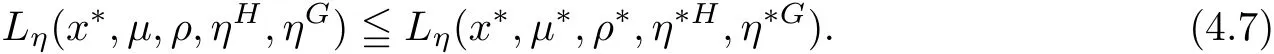
5 Conclusion
 Acta Mathematica Scientia(English Series)2019年2期
Acta Mathematica Scientia(English Series)2019年2期
