RADIAL CONVEX SOLUTIONS OF A SINGULAR DIRICHLET PROBLEM WITH THE MEAN CURVATURE OPERATOR IN MINKOWSKI SPACE∗
Zaitao LIANG(梁载涛)
School of Mathematics and Big Data,Anhui University of Science and Technology,Huainan 232001,China E-mail:liangzaitao@sina.cn;ztliang@aust.edu.cn
Yanjuan YANG(杨艳娟)†
College of Sciences,Hohai University,Nanjing 210098,China E-mail:yjyang90@163.com
Abstract In this paper,we study the existence of nontrivial radial convex solutions of a singular Dirichlet problem involving the mean curvature operator in Minkowski space.The proof is based on a well-known fixed point theorem in cones.We deal with more general nonlinear term than those in the literature.
Key words radial convex solutions;singular Dirichlet problem;mean curvature operator;fixed point theorem in cones
1 Introduction
The Dirichlet problems involving the mean curvature operator in Minkowski space are originated from the study of spacelike submanifolds of codimension one in the flat Minkowski space with prescribed mean extrinsic curvature[1,18],and have been attracted much attention by many researchers.During the past few years,the existence of radial solutions for such problems has been studied in literatures.See[2–6,8–10,15–17,19,20]and the references therein.For example,Bereanu et al.in[4]studied the existence of radial solutions for the following Dirichlet problem
where B(R)={x ∈ RN:|x|
Motivated by the works mentioned above,we continue to study this topic.In this paper,we study the existence of nontrivial radial convex solutions for the following singular Dirichlet problem

where f(t,u)is nonnegative and continuous in(t,u)∈ [0,1]×[0,1)and may be singular at u=1.For the radial symmetric solution v(x)=ω(r)with r=|x|,then problem(1.2)reduces to the following boundary value problem

A nontrivial convex solution of problem(1.3)is negative in[0,1].Here,ω(r)is a convex solution of the problem(1.3)if ω(r)satis fies(1.3)and is a convex function in[0,1].Taking the change of variables u(r)=−ω(r),problem(1.3)is then transformed into
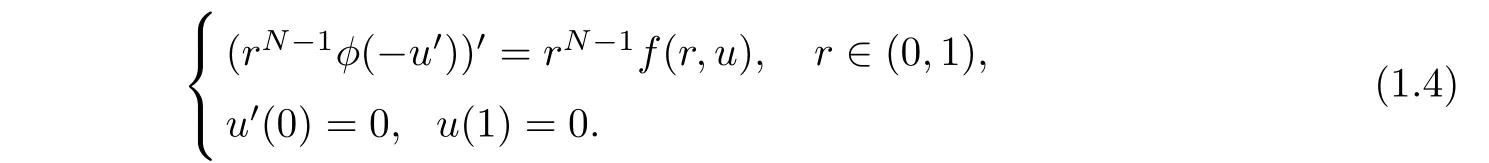
Obviously,the positive concave solutions of problem(1.4)correspond to the nontrivial convex solutions of problem(1.3).Therefore,we just need to study the existence of positive concave solutions of problem(1.4).
In this paper,by applying a well-known fixed point theorem in cones[13],we first establish some existence criteria for positive concave solutions of problem(1.4),and then use such criteria to prove our main results.We should address here that our results presented in this paper have several novelties.First of all,up to our knowledge,it is the first time to study the existence of nontrivial radial convex solutions for Dirichlet problems with the mean curvature operator in Minkowski space.Second,the nonlinear term we deal with is more general than those in some known results,because they assume that the nonlinear terms are sublinear or superlinear at u=0 and u=1 with respect to φ(v).Our results include not only these cases but also some other interesting situations.For example,the case
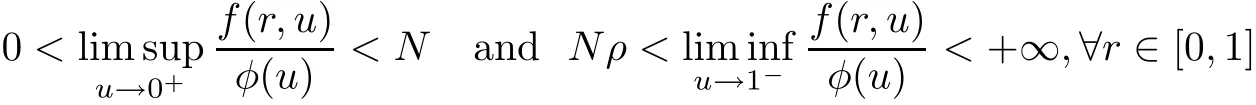
and the case

where ρ >0 is a constant with,σ is a positive constant with
The rest part of this paper is organized as follows.In Section 2,we present some preliminary results.The main results of this paper are presented and proved in Section 3.
2 Preliminaries
Let X be a real Banach space and K be a closed,nonempty subset of X.If Ω is a subset of X,we use the notion

Lemma 2.1(see[13]) Let K be a cone in X.Assume that Ωaand Ωbare open bounded subsets of X with.Let T:be a compact and continuous operator such that

Then T has at least one fixed point in.The same conclusion holds if(i)holds on∂KΩband(ii)holds on∂KΩa.
Such a method was used in[7]to study the positive periodic solutions and eigenvalue intervals for systems of second order di ff erential equations.
In order to apply Lemma 2.1 to problem(1.4),we take X=C[0,1]with

De fine K to be a cone in X by
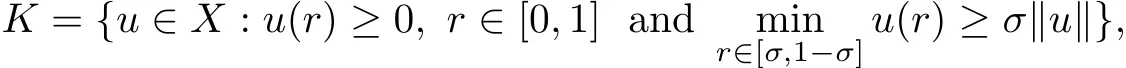
where σ is a positive constant with 0< σ <.Let

Before stating our main results,we need recall the following results.
Lemma 2.2(see[12,14]) The sets Ωaand Bahave the following properties

Obviously,the sets Ωaare unbounded for each a>0,so we can not apply Lemma 2.1 toΩa.Next,for each b>a,we claim that

which make it possible for us to apply Lemma 2.1.The first equality follows directly from(ii).For the second one,it is obvious that.By(iii),,we have
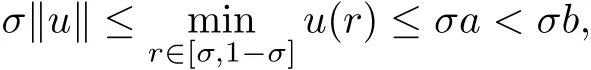
The following lemma is a direct consequence of[11,Lemma 2.2].
Lemma 2.3For any function u ∈ C([0,1],[0,∞))with u′(r)is decreasing in[0,1],we have

Simple computations lead to the following lemma.
Lemma 2.4De fine φ :(−1,1)→ R by.Then

and
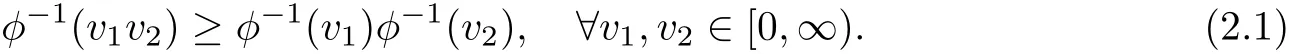
3 Main Results
We de fine a nonlinear operator T onas follows
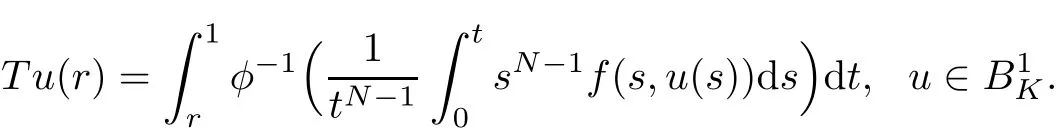

which implies that Tu(r)is decreasing on[0,1].Then we have
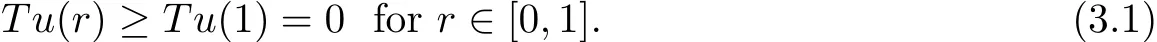
Note that
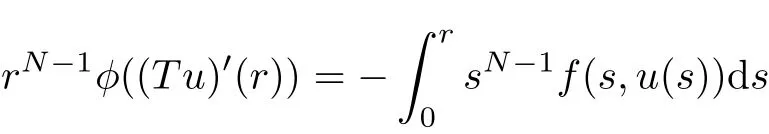
is decreasing on[0,1].Then it follows from φ is increasing and N ≥ 1 that(Tu)′(r)is decreasing on[0,1].By Lemma 2.3,we have

From(3.1)and(3.2),we know that⊂K.By a standard argument,it is easy to prove that T is compact and continuous onfor all a∈(0,1)(see[4,19]).
Theorem 3.1Suppose that the following two hypotheses are satis fied.
(H1) There exist positive constants c∈(0,1),α>0,and a nondecreasing function ϕ1∈ C([0,1),[0,∞))such that
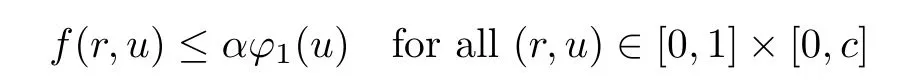
with αϕ1(c)≤ Nφ(c);
(H2) There exist positive constants d∈(0,1),β>0,and a nondecreasing function ϕ2∈ C([0,1),[0,∞))such that
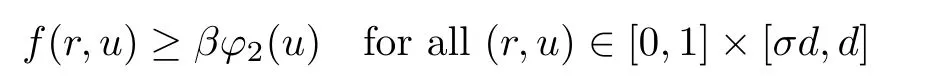
with

Then the following two conclusions hold
(C1)If c<σd,then problem(1.4)has at least one positive concave solution u satisfying
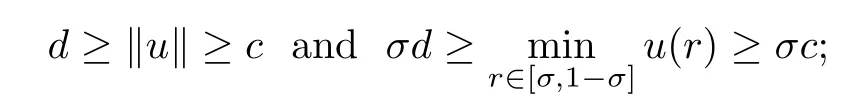
(C2)If c>d,then problem(1.4)has at least one positive concave solution u satisfying
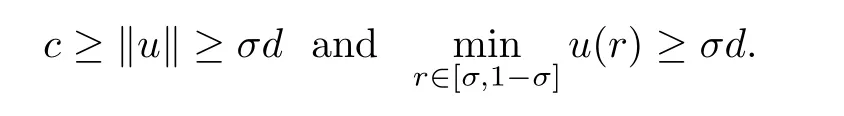
ProofBy Lemma 2.1,we need to prove that
(i)kTuk≤kuk for u∈∂KBc,
(ii)there exists e∈ K{0}such that u 6=Tu+λe for u∈ ∂KΩdand λ >0.
We first consider(i).By(H1),for any u∈∂KBcand r∈[0,1],we have
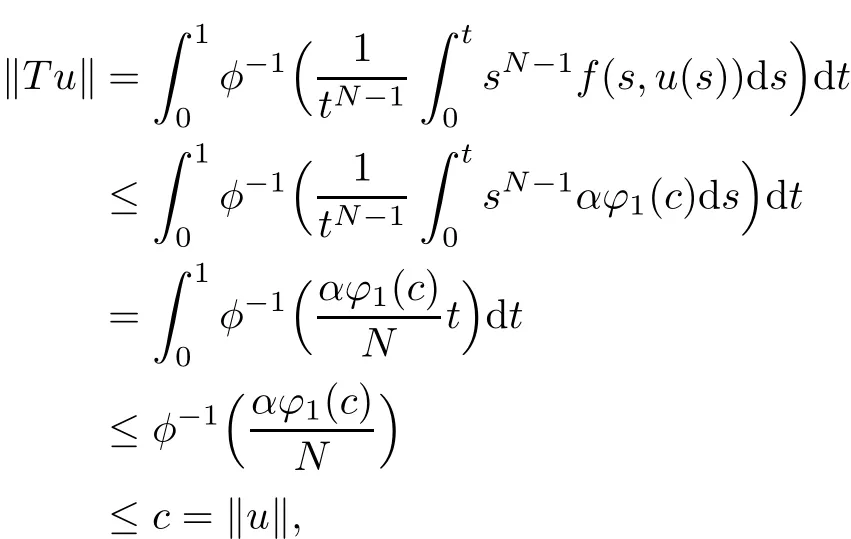
which means that(i)holds.
Now we consider(ii).Let e≡1∈K{0},we claim that
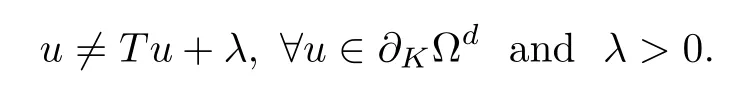
Otherwise,assume that there exist u0∈ ∂KΩdand λ0>0 such that u0=Tu0+ λ0.Since u0∈∂KΩd,by property(iv)of Lemma 2.2,we have

Then by(2.1)and(H2),for any r∈ [σ,1−σ],we have
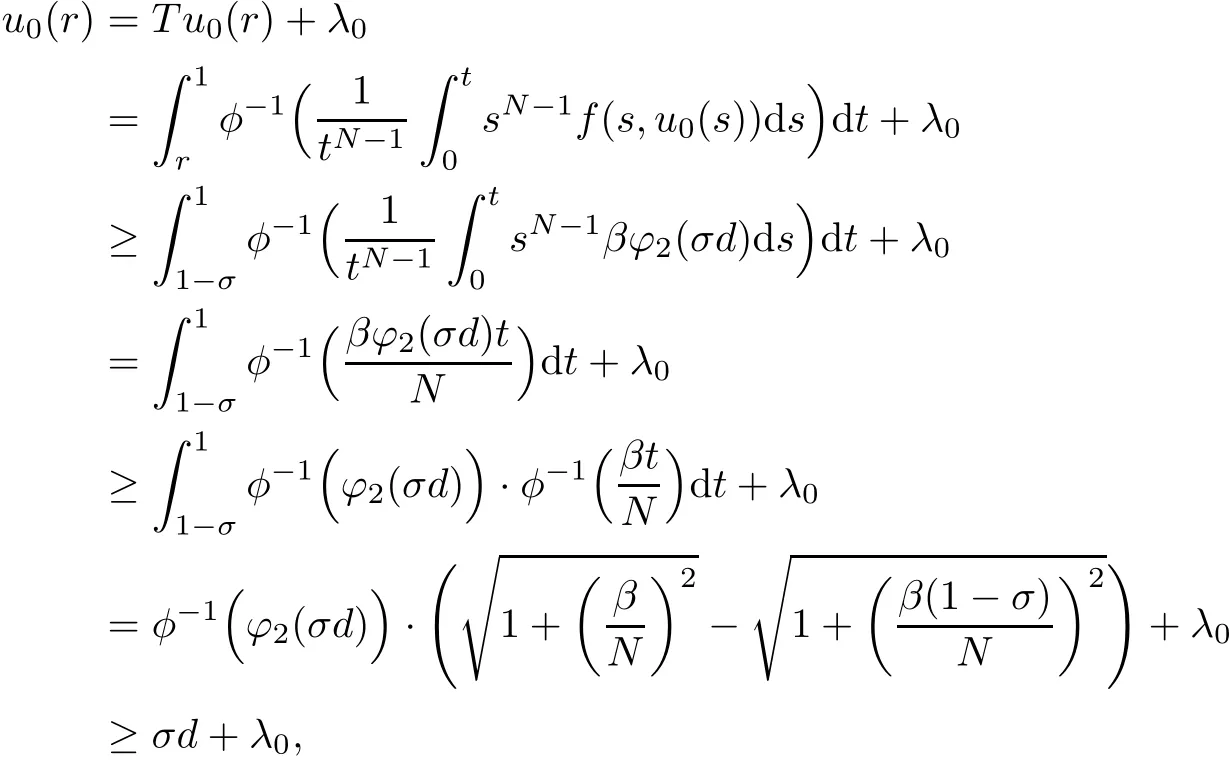
which implies that
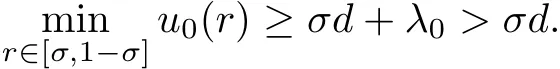
This contradicts property(iii)of Lemma 2.2.Such contradiction shows that(ii)holds.
If c<σd,it follows from property(ii)of Lemma 2.2 that

Then by Lemma 2.1,we know that T has at least one positive fixed point,which satis fiesand kuk ≥ c.Furthermore,we haveσkuk,which yields kuk≤ d.Hence conclusion(C1)holds.
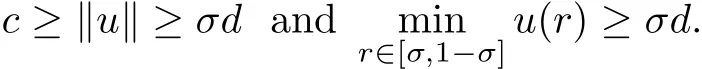
Thus conclusion(C2)holds.
Finally,by applying Theorem 3.1,we state and prove our main result.To this aim,we introduce the following assumption.
(H3)There exist nonnegative functions li:[0,1]→ [0,∞),i=1,···,4 such that
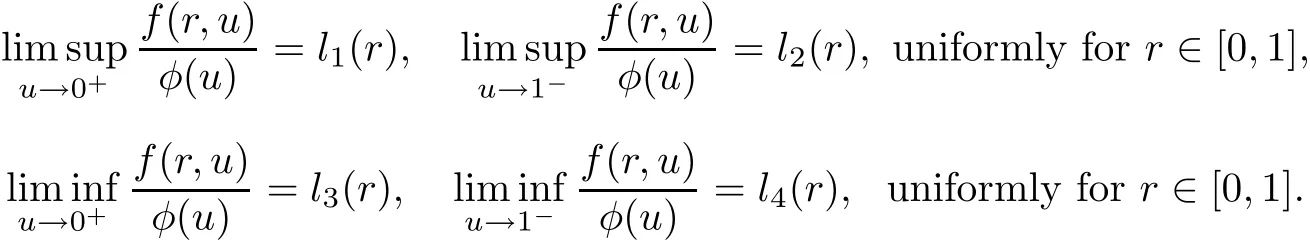
Theorem 3.2Assume that(H3)holds.Then problem(1.2)has at least one nontrivial radial convex solution if one of the following conditions holds.
(H4)0≤l1(r) (H5)0≤l2(r) ProofWe just need to prove the case when(H4)holds.The case when(H5)holds is completely analogous. It follows from 0≤l1(r) Choosing α =N and ϕ1(u)= φ(u),then we have and Thus(H1)holds. It follows from Nρ Choosing β =Nρ and ϕ2(u)= φ(u),then and Hence(H2)holds.Then by Theorem 3.1,we know that problem(1.2)has at least one nontrivial radial convex solution. ? In order to illustrate our main results,we present an example as follows. Example 3.3Consider the following problem where a:[0,1]→[0,∞)with a(r)>0 for r∈(0,1]. Theorem 3.4The following results hold (C3)Problem(3.3)has at least one nontrivial radial convex solution if p>1 and q>. (C4)Problem(3.3)has at least one nontrivial radial convex solution if 0 ProofProblem(3.3)can be regarded as a problem of form(1.2),where uniformly for r∈[0,1].If 0 Therefore,by applying Theorem 3.2,we know that conclusions(C3)and(C4)hold. ? AcknowledgementsWe would like to show our thanks to Professor Jifeng Chu(Shanghai Normal University)for useful discussions.
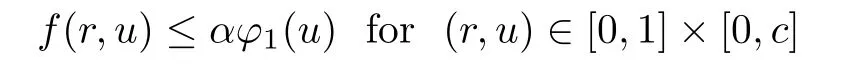

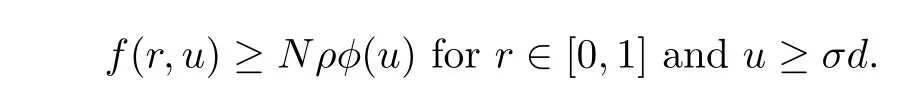
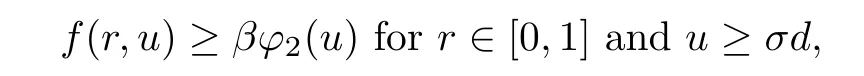
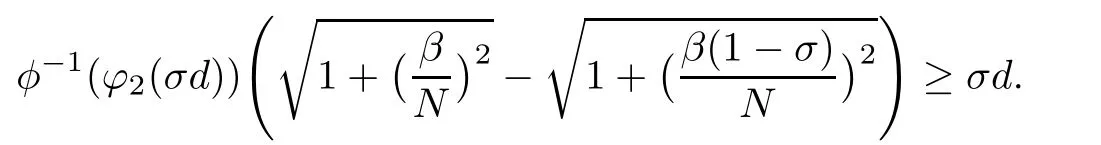

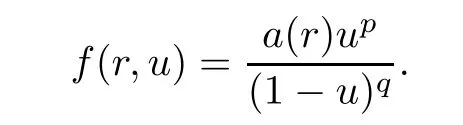
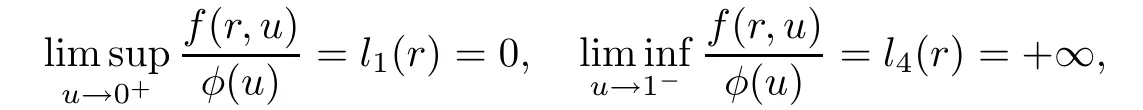

 Acta Mathematica Scientia(English Series)2019年2期
Acta Mathematica Scientia(English Series)2019年2期
