地表反照率不同计算方法对干旱区流域蒸散反演结果的影响——以新疆三工河流域为例

张振宇,李小玉,孙 浩

1 浙江农林大学林业与生物技术学院, 杭州 311300 2 中国科学院新疆生态与地理研究所荒漠与绿洲生态国家重点实验室, 乌鲁木齐 830011 3 中国科学院大学,北京 100049

地表蒸散(Evapotranspiration,简称ET)是地球表面与大气相互作用过程中的关键一环,是地球水量平衡的重要组成部分,地表蒸散的过程伴随着能量的吸收与释放,也是维持地球能量平衡的重要环节。近年来,针对全球气候变化的研究不断深入,对地表蒸散的研究也越来越多,在这个过程中产生了较多的ET估算模型,如SEBAL模型[1]、SEBS模型[2]、ETwatch模型[3]等,其中SEBAL模型是应用最为广泛的ET估算模型之一。SEBAL模型是由Bastiaanssen提出的一种地表蒸散估算模型,研究者利用SEBAL模型结合不同种类遥感数据进行了不同区域的蒸散反演,并且取得了较好的反演结果。Santos[4]利用Landsat5 TM数据结合SEBAL模型进行了巴西布吉达河流域蒸散反演,Rawat等[5]基于Landsat7 TM数据和SEBAL模型对印度哈里亚邦区域的小麦农田进行了蒸散反演,Alemayehu等[6]利用MODIS数据结合SEBAL模型进行了东非玛拉盆地的地表蒸散估算。曾丽红、杜嘉等[7-9]利用Landsat TM和MODIS数据结合SEBAL模型对中国东北地区的扎龙湿地、三江平原以及松嫩平原地区进行了蒸散量的反演与分析；张殿君等[10]利用SEBAL模型对中国黄土高原典型流域区进行了蒸散反演,并讨论了土地利用对蒸散的影响；张发耀等[11]利用MODIS数据结合SEBAL模型对浙江省蒸散量进行了估算；王秋云[12]利用SEBAL模型进行了北京平原造林区的蒸散研究；周玲等[13]基于Landsat TM/ETM+数据,应用SEBAL模型对中国西南地区漓江流域进行了蒸散量变化分析；杨肖丽等[14]利用MODIS数据和SEBAL模型对中国半干旱区的老哈河流域进行了蒸散研究；李宝富、陈亚宁等[15]利用TM数据,结合SEBAL模型对中国干旱区的塔里木河干流区进行了蒸散估算；张楠楠等[16]利用HJ- 1B数据结合SEBAL模型对淮河上游段进行了蒸散估算。以上研究都是利用SEBAL模型实现了地表蒸散的反演,而对SEBAL模型的参数计算方法影响讨论较少,只有少数研究讨论了SEBAL模型反演结果受气象条件[17]和地表类型的影响。地表反照率,是指地表物体各个方向上发射的太阳辐射通量与到达该物体表面上的总辐射通量之比,是各个方向上反射率的积分。地表反照率是影响地球能量平衡的关键变量,相关研究[18-19]表明,地表反照率的增加促使地表净辐射减少,造成区域降水和云量的降低,同时,云量的减少使得地表净辐射通量进一步增大,促进降水和云的形成,这种反馈作用维持着区域气候与热量的稳定与平衡。在遥感反演研究中,针对同一物理量的多种求解方法可能导致衍生结果的差异。地表反照率作为影响地表能量平衡的关键变量,是SEBAL模型的重要参数,分析不同地表反照率计算方法造成的SEBAL模型反演结果差异,对提高SEBAL模型反演精度具有重要意义。本文拟在控制SEBAL模型其他参数一致的基础上,基于两种地表反照率计算方法,对研究区进行蒸散反演,通过反演值与实测值的拟合程度、偏离程度差异,实现不同地表反照率计算方法对SEBAL模型的影响分析。

1 研究区概况

三工河流域(图1),位于新疆阜康市境内,区域主要由绿洲与部分荒漠构成,地势南高北低。平原区北部为古尔班通古特沙漠,南部为天山山脉,境内自西向东分布有水磨河、三工河、四工河3条河流,区域内干旱少雨,年降水量150—240 mm,水资源主要依赖高山冰川和积雪融水。研究区气候类型为典型的温带大陆性气候,夏季日照时间长,热量高,冬季较早,寒冷漫长,流域内主要农作物为小麦、玉米等经济作物。

图1 三工河流域位置示意图Fig.1 Location of Sangong river basin

2 研究数据及预处理

2.1 遥感和其他空间数据获取与预处理

①Landsat 8 OLI/TIRS影像数据来源于美国地质调查局网站(https://glovis.usgs.gov/),共六期,日期分别为2016年5月25日、2016年6月26日、2016年7月12日、2016年7月28日、2016年8月29日和2016年9月30日。影像数据整体云量小于0.6%,其中6月26日和7月12日影像云量较高,分别为1.1%和7.45%。对6期Landsat 8 OLI/TIRS影像数据进行辐射定标、大气校正获取纠正后数据。

②ASTER高程数据来源于马里兰大学全球土地覆盖数据库(http://www.landcover.org/data/),空间分辨率为30 m,对高程数据进行拼接与裁剪得到所需研究区高程数据。

③三工河流域矢量边界由中国科学院新疆遥感与地理信息系统重点实验室提供。

2.2 波文比数据

波文比数据主要来自于中国科学院新疆遥感与地理信息系统重点实验室设立的2台波文比观测站,经纬度坐标分别为(44.33°N,87.89°E)和(44.36°N,87.87°E),波文比观测站放置于均一的农田内部,基于波文比-能量平衡法(BREB)[20]获得瞬时蒸散,进一步获得每小时蒸散和日蒸散。大量研究证明[21-22]利用波文比观测仪器测量蒸散精度较高。波文比数据监测间隔为1h。

3 模型及参数

SEBAL模型[23]的理论基础是地表能量平衡方程,即地表的净辐射通量由从下垫面到大气的感热通量、从下垫面到大气的潜热通量和土壤热通量组成：

Rn=G+H+λET

(1)

式中,Rn代表净辐射通量(W/m2),G代表土壤热通量(W/m2),H代表感热通量(W/m2),λET代表潜热通量(W/m2),λ代表水的汽化潜热,通常为2.49×106W m-2mm-1；ET表示蒸散量,kg m-1s-1。

3.1 净辐射通量(Rn)计算

净辐射通量计算公式为：

Rn=(1-a)Rsd+Rld-Rlu-(1-k)Rld

(2)

式中,a为地表反照率,Rsd为太阳下行短波辐射(W/m2),Rld为太阳下行长波辐射(W/m2),Rlu为地表反射的长波辐射(W/m2),k为地表比辐射率(发射率)。

3.2 土壤热通量(G)的计算

土壤热通量是单位时间、单位面积上的土壤热交换量,一般存储在土壤和植被中,这部分能量在整个热量平衡过程中占比重较小,而且计算较为困难,这里使用曾丽红[24]推导的公式。

(3)

式中,Ts为地表温度,NDVI为归一化植被指数,c表示卫星过境时间对G的影响,过境时间在地方时12：00点以前取0.9；在12：00点到14：00点之间取1.0；在14：00点到16：00点之间取1.1。

3.3 感热通量(H)的计算

感热通量表征的是下垫面与大气间的湍流形式的热量交换,与大气稳定度、风速、表面粗糙度有关。通用计算公式如下：

(4)

式中,Pair为空气密度(kg/m3)；Cp是空气定压比热(1004 J kg-1K-1)；dT是距离地面高Z1和Z2处的温差(一般Z1为0.1 m,Z2为2 m),rah为空气动力学阻抗。

3.4 小时蒸散量与日蒸散量计算

小时蒸散量的计算公式[25]为：

(5)

λ=2.501-0.002361×(Ts-273.15)

(6)

式中,λ为水的汽化潜热,ET为蒸散量,ETinst为小时蒸散量。

通过小时蒸散量结合日照时长计算日蒸散量ETday：

(7)

式中,N为区域内平均日照时长,t为日出到卫星过境时间间隔(h)。

4 地表反照率计算

4.1 基于各波段反射率的大气表观反射率计算

求取大气表观反射率,这一过程在辐射定标中即可完成：

(8)

式中,ρ代表表观反射率,DN为影像灰度值,μ、φ分别为landsat8 OLI/TIRS影像的反射率增量和修正值,θ为太阳高度角。

4.2 求取地表反照率

①Liang地表反照率计算方法(下称Liang方法)[26]:

(9)

式中,ρ2、ρ4、ρ5、ρ6、ρ7为各波段大气表观反射率,ap为大气程辐射值影响,一般取0.03,tsw为大气单向透过率。

大气单向透过率计算公式如下[27]：

tsw=0.75+2×10-5×Z

(10)

式中,Z为海拔高度(m),从DEM数据中获取。

②Smith地表反照率计算方法(下称Smith方法)[28]:

(11)

式中,ρi为波段反射率(对于Landsat 8 OLI/TIRS数据使用2、4、5、6、7波段),Δλi为各波段范围,Si为1—7波段的平均太阳辐照度(表1),ap为大气程辐射值影响,一般取0.03,tsw为大气单向透过率。

表1 Landsat 8 OLI数据波段平均太阳辐照度[28]

Si,平均太阳辐照度,Average solar irradiance

5 结果与分析

5.1 日蒸散量比较

基于SEBAL模型得到两种地表反照率计算方法下反演的地表日均蒸散量(表2)及其空间分布图(图2和图3),对比6个研究日区域日蒸散量的分布,结果显示两种地表反照率方法下最终得到的日蒸散量空间和时间分布规律保持一致。时间上,日蒸散量在6月—7月末明显高于其他月份；空间上,流域绿洲的日蒸散量明显高于其他类型区域(水体除外)；另一方面,两种地表反照率方法下基于SEBAL模型得到的日蒸散量分布曲线(图4)则有较大不同。5月25日,两种地表反照率方法下的日蒸散量分布曲线在形态上保持一致,但是Liang方法下的日蒸散量分布曲线在6 mm/d处开始接近横坐标轴,而Smith方法下日蒸散量分布曲线在日蒸散量7 mm/d处才开始接近横坐标轴。6月26日、7月12日、7月28日三天同一地表反照率计算方法下的日蒸散量分布曲线形态上较为一致,但是不同地表反照率计算方法下得到的曲线则差异较大：Liang方法下得到的3期日蒸散量分布曲线波峰出现在日蒸散量4 mm/d附近,在日蒸散量6 mm/d处开始接近横坐标轴,而Smith方法下的3期日蒸散量分布曲线均在日蒸散量6—6.5 mm/d处达到峰值,在日蒸散量7.5 mm/d处才开始接近横坐标轴。8月29日和9月30日两期日蒸散量分布曲线则呈现出与前4期较为不同的特征：曲线波峰开始向低日蒸散量区间移动,Liang方法下得到的日蒸散量分布曲线波峰分布在日蒸散量1—1.5 mm/d附近,而Smith方法下得到的日蒸散量分布曲线在日蒸散量1.5—2.5 mm/d处达到峰值。两种方法下最终得到的多条日蒸散量分布曲线在日蒸散量区间末端均出现了一个较为明显的波峰,是由区域内的水库水体所引起。总的来说,Smith方法下基于SEBAL模型反演的区域日蒸散量分布曲线峰值出现更晚。

此外,两种地表反照率计算方法下最终求得的日均蒸散量也有较大差异,Liang方法下最终得到的区域日均蒸散量在所选取的6个研究日内均小于Smith方法下最终得到的结果,其中,春季(5月25日)、秋季(8月29日和9月30日)的日均蒸散量差距较小,平均差异0.2 mm/d,而夏季(6月26日、7月12日、7月28日)的日均蒸散量差距较大,平均差异0.64 mm/d。

表2 两种地表反照率计算方法下得到的区域日均蒸散量/(mm/d)

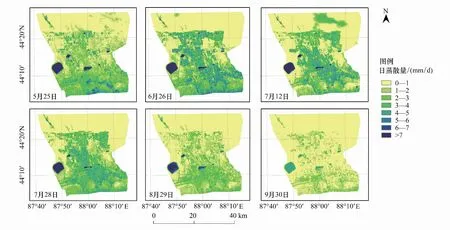
图2 Liang地表反照率计算方法下日蒸散量分布Fig.2 Daily evapotranspiration distribution using Liang surface albedo formula

图3 Smith地表反照率计算方法下日蒸散量分布Fig.3 Daily evapotranspiration distribution using Smith surface albedo formula

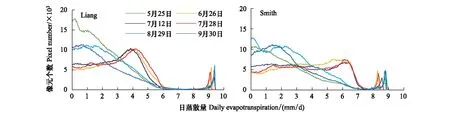
图4 Liang反照率计算方法和Smith反照率计算方法下的日蒸散量分布曲线Fig.4 Distribution curve of daily evapotranspiration using Liang and Smith surface albedo method

5.2 两种地表反照率计算方法下的日蒸散反演精度比较

将SEBAL模型反演值与实测值进行拟合,并使用决定系数R2、均方根误差RMSE、平均偏差BIAS和平均绝对偏差MAE[29]对两种地表反照率方法下基于SEBAL模型反演的日蒸散量进行比较与评价。评价指标计算公式如下:

(10)

(11)

(12)

式中,N为观测个数,Pi为反演值,Qi为实测值。得到的结果如表3所示。

表3 两种地表反照率计算方法下SEBAL模型反演值精度比较

R2,决定系数,Coefficient of determination；RMSE,均方根误差,Root mean square error；BIAS,平均偏差,Bias；MAE,平均绝对偏差,Mean absolute error

两种地表反照率计算方法下基于SEBAL模型反演的日蒸散量与实测值散点图及拟合方程(图5)表明,Smith方法下最终得到的日蒸散量与实测值的线性拟合程度更高,决定系数达到了0.85,相比之下,Liang方法下得到的模型反演日蒸散量与实测值的线性拟合决定系数仅为0.76；F检验显示,Smith方法下最终得到反演值与实测值线性拟合P值<0.001,而Liang反照率计算方法下得到的拟合直线P值为0.0016,大于0.001,可见相同时间空间条件下,Smith方法下基于SEBAL模型得到的日蒸散量与实测值更为接近,可信程度更高。另外通过RMSE、BIAS、MAE 3种指标对反演值与实测值进行偏离程度分析,Smith方法下最终得到的日蒸散量与实测值的偏离程度小于使用Liang方法下得到的结果,多项结果表明：在应用SEBAL模型对干旱区地表进行蒸散反演过程中,使用Smith方法结果作为SEBAL模型地表反照率参数输入更优。

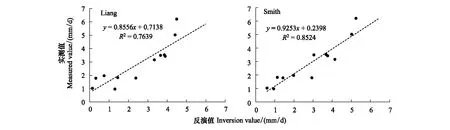
图5 Liang反照率计算方法和Smith反照率计算方法下的日蒸散量拟合Fig.5 Daily evapotranspiration fitting using Liang and Smith surface albedo method

6 讨论

6.1 两种方法计算下的地表反照率比较

2016年6个研究日的流域地表反照率分布曲线(图6)表明,两种方法得到的地表反照率分布曲线类似,都呈较明显的正态分布,然而不同方法下的曲线波峰处反照率存在明显差异,基于Liang方法得到的地表反照率分布曲线波峰处反照率在6个时期均高于Smith方法得到的曲线波峰反照率,波峰处地表反照率相差0.02—0.06,尽管这种差异较小,但是这种差异使得整个区域的反照率分布出现较大不同,Smith方法下得到的地表反照率更低,两种方法计算出的地表反照率均值(表4)可进一步印证这一点,地表反照率的差异使得由此计算出的流域净辐射通量、显热通量产生了更大的差异,进一步的造成了两种地表反照率计算方法下基于SEBAL模型反演结果在分布上的差异。

图6 两种方法计算下反照率像元分布曲线Fig.6 Albedo pixel distribution curves under two methods

地表反照率计算方法Surface albedo calculation method5月25日May 25th6月26日June 26th7月12日July 12th7月28日July 28th8月29日August 29th9月30日September 30thLiang0.36380.34690.32850.31830.30130.2916Smith0.29440.26840.25520.25580.25200.2520

6.2 两种方法计算下地表反照率与MCD43A3产品的比较

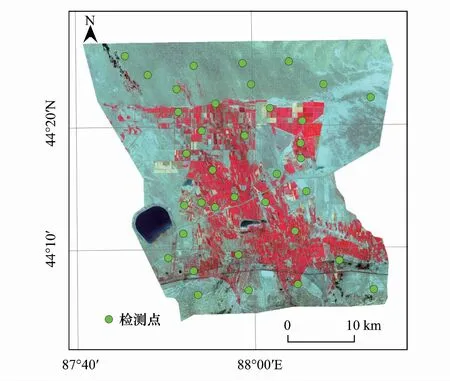
图7 地表反照率检测点位置Fig.7 Location of surface albedo detection points

为进一步比较两种方法计算出的地表反照率在研究区的可靠性,在缺乏地表反照率测量仪器的情况下,参考He等[30]的方法,使用MODIS地表反照率产品MCD43A3与两种方法计算出的地表反照率进行比较,由于研究区所选Landsat 8数据云量均较少(晴空条件),因此提取MCD43A3数据中的短波白空反照率(WSA)作为参考标准。在研究区内部随机布置了36个监测点(图7),通过6个研究日共得到216个数据。数据比对结果(图8)表明：①两种方法下得到的地表反照率均偏高于MCD43A3 WSA,Liang方法计算出的地表反照率与MCD43A3 WSA拟合程度(R2=0.35)略高于Smith方法计算结果(R2=0.2),说明Liang方法计算出的地表反照率一致性更好。②RMSE比较上,Smith方法计算出的地表反照率与MCD43A3 WSA误差相对较小(Smith方法RMSE=0.075；Liang方法RMSE=0.13)。

图8 两种方法计算下地表反照率与MCD43A3短波白空反照率对比Fig.8 Comparison between surface albedo calculated by two methods and MCD43A3 shortwave white sky albedo

同时由于Landsat 8数据部分参数官方尚未明确公布,计算Landsat 8数据地表反照率时仍采用针对上一代传感器的方法,这也可能会对结果造成一定影响；基于此,Smith提出了针对Landsat 8数据地表反照率的计算方法,并在阿拉斯加、佛罗里达等地区进行了实验,近期部分学者[30]提出利用大气顶反照率和站点测量数据直接估计Landsat 8地表反照率,实验效果较好,但由于中国西北地区缺少地表反照率国际测量站点,因此,各种方法在中国西北地区的适用性仍有待进一步检验。

另一方面,由于USGS(美国地质调查局)至今未公布Landsat 8数据各波段平均太阳辐照度,因此在使用Smith方法过程中使用了其提供的各波段平均太阳辐照度。在理想状态下,平均太阳辐照度可通过大气光谱曲线和各波段响应函数获得,分别使用WRC太阳光谱曲线和Thuillier 太阳光谱曲线结合Landsat 8数据1—7波段响应函数进行平均太阳辐照度估计[31-32],结果(表5)显示,两种谱线对应的波段平均太阳辐照度存在差异,其中1和4波段差异较大,其他波段结果相近,同时Smith方法的1、2、3波段平均太阳辐照度均小于两种谱线对应估计值,而在第6波段(短波红外)上高于谱线估计值,这使得Smith方法在计算地表反照率时更侧重于短波红外波段,而由此得出的地表反照率与相关产品的偏差较小,这说明Landsat 8地表反照率计算中短波红外波段的权重增加可能改善了研究区地表反照率反演质量,部分研究[33]也表达了相似的结果。

表5 利用Thuillier和WRC太阳光谱曲线估算的Landsat 8 OLI数据各波段平均太阳辐照度

ThuillierSi,利用Thuillier太阳光谱曲线估算的波段平均太阳辐照度,Band average solar irradiance based on Thuillier Solar spectral curve；WRCSi,利用WRC太阳光谱曲线估算的波段平均太阳辐照度,Band average solar irradiance based on WRC Solar spectral curve

7 结论

研究基于两种地表反照率计算方法结合SEBAL模型,对西北干旱区典型流域日蒸散进行反演并进行比较,结果表明：(1)Simth方法下最终得到的日均蒸散量均高于Liang方法下最终得到的日均蒸散量,这种差异在夏季最明显。同时,Smith方法下基于SEBAL模型得到的反演结果与实测值的拟合程度和偏离程度略优于Liang方法下得到的结果。(2)两种方法计算的地表反照率差异是导致SEBAL模型反演日蒸散量差异的主要原因,相同日期内Liang方法得到的地表反照率均高于Smtih方法结果(高约0.04—0.08)。(3)与MCD43A3产品的比较结果显示,Liang方法得到的地表反照率与MCD43A3产品一致性较好,但是其偏离程度也较高。综合考虑之下,Smith方法在研究区的适用性略好。