基于机器学习与空间映射的滤波器优化方法*

胡 聪，赵建平，张仕顺，杨 君，徐 娟

（曲阜师范大学，山东 曲阜 273165）

0 引 言

微波滤波器是通信系统必不可少的组成部分。随着无线通信与微波技术的发展，系统对微波滤波器的设计要求越来越高。为了满足不同的需求，需要不断优化滤波器。使用传统的空间映射方法[1］优化设计滤波器时，为了寻找粗模型和细模型之间的对应关系，需要进行复杂的计算，耗费大量的时间，影响滤波器的优化效率。因此，寻找一种省时高效的优化方法显得十分重要。

鉴于此，本文提出采用机器学习的方法来得到粗模型和细模型之间的对应关系，使用机器学习代替传统空间映射方法的参数提取过程，以大大减小优化滤波器的计算复杂性和优化过程所耗费的时间，提高优化的效率。

1 基于机器学习的空间映射

1.1 空间映射方法

原始的空间映射方法由John W.Bander等人在1994年首次提出，是一种集电磁场数值计算方法的精确性和电路理论计算方法的快速性优点于一身的优化设计方法。

原始空间映射方法假定两模型设计参数之间是线性映射关系，但在实际工程中多是非线性问题，导致该方法应用范围具有局限性。后来，经过发展又相继提出了主动空间映射方法、置信域主动空间映射方法和隐式空间映射方法等[2］。

在空间映射方法中，一个微波结构被用两种模型表示[3］：一种是仿真快速、高效，但是仿真结果不精确的粗模型；一种是仿真精度高，但是耗时长的细模型。空间映射方法的思想[4］是假定上述两个模型设计参数之间存在映射关系，通过构建它们之间的映射关系，把繁琐冗杂的优化工作交给仿真快速高效的粗模型来完成，而细模型只用来验证优化结果是否满足要求。

空间映射方法的优化问题定义为[5］：

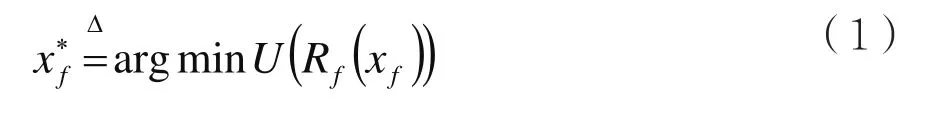
其中，R∈ ℜm×1是模型的m个响应点组成的f响应矢量，m代表响应时的频率点；= ℜn×1代表由n个参数组成的参数矢量；U是合适的目标函数；是精确空间参数的待定优化值，选取唯一。

设xc和xf分别是粗模型和细模型的设计参数，Rc和Rf分别是粗模型和细模型的响应，如果能够找到联系细模型和粗模型设计参数的一个映射P：

使得：

即在细模型中xf参数下的响应与在粗模型中P(xc)参数下的响应一致。

这样就可以通过优化粗模型得到其优化值，然后对进行映射得到：

王建磐教授师从中国著名数学家曹锡华教授，于1982年在华东师范大学获理学博士学位，是新中国首批自己培养的18名博士之一，是中国最早涉猎代数群与量子群领域的数学家之一，是代数群表示的国内领军人物．作为数学家，除了做数学研究和培养基础数学的博士生之外，他十分关注数学教育学科的建设与发展，积极推动中国数学教育研究国际化．从1999年起，在王建磐和顾泠沅的呼吁和积极组织下，建立了中国第一批数学教育博士培养点，培养了数学教育方面的博士．王建磐教授曾任华东师范大学校长，是中国著名的数学家和教育家．

即可作为细模型优化值的近似，从而避免直接对细模型进行优化。

1.2 机器学习

在空间映射方法中，最关键的部分是粗模型和细模型之间映射关系的确定。本文采用机器学习来构建其映射关系。机器学习的方法众多[6］，本文采用多分类支持向量机方法[7］。

支持向量机[8］于1963年被提出，在20世纪90年代后得到快速发展，并衍生出一系列改进和扩展算法，包括多分类SVM、最小二乘SVM（Least-Square SVM，LS-SVM）、支持向量回归（Support Vector Regression，SVR）、支持向量聚类（Support Vector Clustering）和半监督SVM（Semi-Supervised SVM，S3VM）等。

SVM的优化问题同时考虑了经验风险和结构风险最小化，因此具有稳定性。在进行决策时，支持向量机决策边界仅由支持向量决定，其余的样本点不参与经验风险最小化，因此具有稀疏性。在使用核方法的非线性学习中，支持向量机的稳健性和稀疏性在确保可靠求解结果的同时降低了核矩阵的计算量和内存开销，并使其具有良好的泛化能力。

需要说明的是，在进行机器学习的过程中，最重要的环节是选取样本。样本选取的好坏直接影响机器学习的结果。在本文提出的方法中，首先需要给出少量的样本（至少2组对应关系），然后通过不断的机器学习过程自动添加样本。这种方法一方面增加了样本数量，使机器学习的结果更精确；另一方面使机器学习的样本更趋近于优化指标。

1.3 基于机器学习的空间映射优化流程

（1）给出滤波器性能指标；

（2）优化粗模型，找出其最佳设计参量；

（3）给出n个细模型参数xf(1)、xf(2)…xf(n)，优化粗模型，使粗模型响应逼近细模型响应，分别得到粗模型中参数xc(1)、xc(2)…xc(n)；

（4） 将 参 数xf(1)、xf(2)…xf(n)和xc(1)、xc(2)…xc(n)作为n组对应关系的样本添加到支持向量机的机器学习程序中，把最佳设计参量作为目标进行机器学习，得到细模型的参数；

（5）初始化i=1；

（6）把代入细模型中进行验证，看优化结果是否满足设计要求，若满足，则结束优化；若不满足，则优化粗模型，使粗模型响应逼近细模型响应，得到粗模型中的参数；

（7）把和作为一组样本添加到支持向量机的机器学习程序中，把最佳设计参量作为目标进行机器学习，令i=i+1得到细模型的参数，转到步骤（6），直到满足优化指标要求。

2 带通滤波器优化实例

滤波器优化指标：

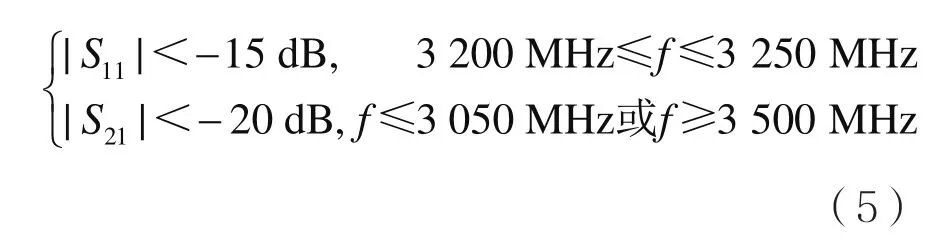
本文要优化的滤波器结构示意图和俯视图如图1所示。该滤波器的性能主要与谐振腔微带线宽度w和谐振腔开口间距大小g有关。由于滤波器结构对称，因此选取细模型的设计参数为谐振腔微带线宽度w和谐振腔开口间距大小g，即xf=[wg］。

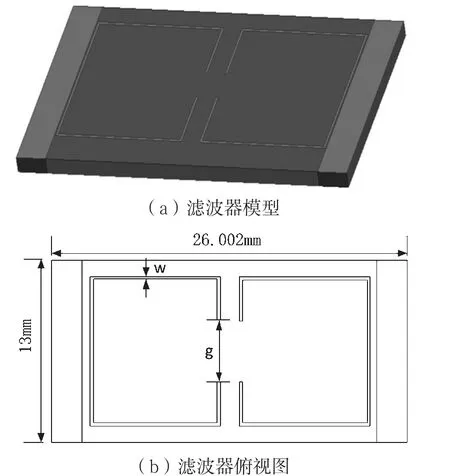
图1 滤波器结构

在ADS软件中建立滤波器的粗模型（等效电路），如图2所示。

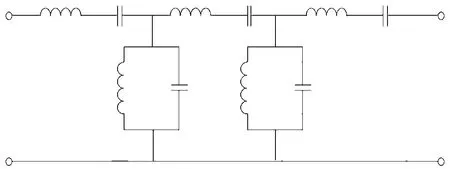
图2 滤波器等效电路

选取粗模型的设计参量（电感单位nH，电容单位pF）为：

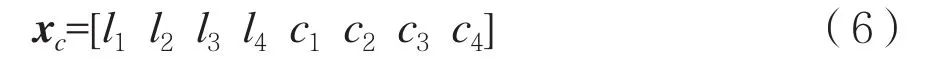
优化粗模型，使其响应满足上述滤波器优化指标，找出其最佳设计参量为：

样本1的细模型设计参量为w=0.11，g=1.9，即xf(1)=[0.11 1.9］时，细模型响应如图3（a）所示。优化粗模型，使粗模型响应逼近细模型响应，得到粗模型的设计参数为：

样本2的细模型设计参量为w=0.17，g=2.1，即xf(2)=[0.17 2.1］时，细模型响应如图3（b）所示。优化粗模型，使粗模型响应逼近细模型响应，得到粗模型的设计参数为：

图3 样本细模型响应

由样本的细模型响应可见，均不符合优化指标。将xf(1)、xc(1)和xf(2)、xc(2)作为两组对应关系的样本输入到支持向量机算法的Matlab程序中，以为目标进行机器学习。在本例中第一次机器学习的输出预测参量为=[0.14 2］，代入细模型中得到细模型的响应结果如图4所示。

图4 第一次机器学习细模型响应

可见，不符合优化指标。优化粗模型，使粗模型响应逼近细模型响应，得到粗模型的设计参数为：

将、作为第三组对应关系的样本添加到支持向量机算法的Matlab程序中，以为目标函数进行第二次机器学习，输出预测参量为：

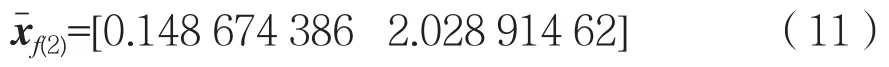
代入细模型，重复上述步骤。

应用基于机器学习的空间映射方法，优化过程共进行69次机器学习，图5给出了方法第68次、第69次机器学习产生的细模型预测参量的细模型响应。可以发现，细模型响应已经满足了优化指标，说明利用该方法对滤波器进行优化是可行的。

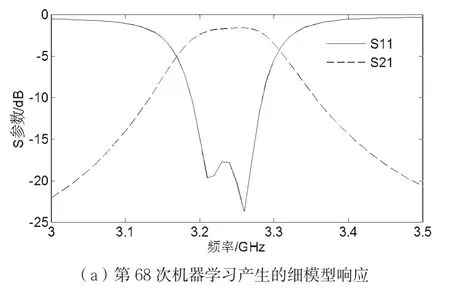
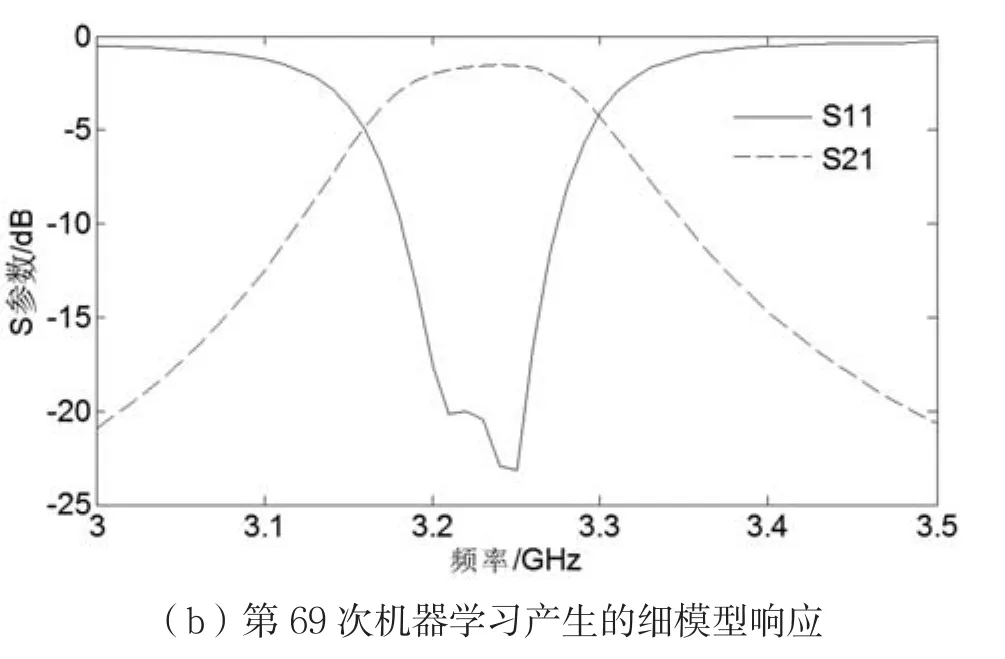
图5 滤波器细模型响应结果

对于上述滤波器的优化，如采用传统的空间映射方法进行一次参数提取，过程将耗时1.5 min。而如果采用机器学习的方法代替该过程，只需0.05 s就可完成，明显减少了参数提取过程的耗时。但是，利用本文方法对滤波器进行优化时，机器学习的次数会有所增加，这一问题还需下一步研究解决。

3 结 语

本文提出了一种用于优化滤波器的基于机器学习的空间映射方法，利用机器学习方法代替传统空间映射方法的参数提取过程，大大节省了该过程所需要的时间，且通过实例成功地对一带通滤波器进行了优化，结果说明该方法具有可行性。