基于复杂网络分析的通信网络节点重要度评估方法*

梁德军，宋广宁，赵 明

（国防科技大学，安徽 合肥230037）

0 引 言

随着信息技术的快速发展，通信网络在承载信息传输方面的作用已日益突出。通信网络是指由多个交换节点用传输链路以一定的拓扑结构互联构成的用于特定功能的复杂网络[1］，而各个通信节点由于其功能作用网络位置和组织关系的不同，其在网络中表现出不同的重要程度[2］，如现代军事战争中斩首行动就是要在繁杂的目标中寻找到最重要或最核心的部位进行打击，以起到意想不到的效果。因此，对通信网络中各通信节点进行重要性评估，准确挖掘出网络中的核心节点，可以为网络抗毁性方面的研究提供重要的理论帮助。

现有关于节点重要性的度量方法可分为两类:第一类方法为在网络的整体能力健全的前提下反映节点的显著程度，一般通过节点在网络拓扑中的中心性程度进行评估，即节点的中心性越强，显著性越明显，节点越重要，典型的指标有度中心介数、子图、紧密性等; 第二类方法为去除掉节点之后分析网络的性能毁坏程度，一般通过网络降低的性能指标来衡量，即去除掉该节点之后，网络性能下降得越多，则该节点越重要，经典方法有节点删除法、收缩法[3］，通过网络中的最短路径、网络效率[4］以及生成数目的下降程度来衡量。最近的研究成果提出了网络中的节点重要性不仅与网络拓扑结构有关，还受传播机制以及节点自身属性影响[5］[6］，然而上述节点重要性的评估方法仅考虑了网络的静态特性，忽略了网络中存在的物质流动给网络带来的影响，并不能很好地反映真实的节点重要程度。而且通信网络存在时变性，随着网络节点的接入和退出拓扑结构发生变化，各个节点在整个通信时段中接入的时段也影响节点的重要度。因此本文提出一种基于局部负载重分配[7］后对近邻节点负载震荡程度的节点重要度评估模型，研究某一时段固定网络拓扑结构的节点重要度，并根据该结构网络在整个通信时段中所处的位置确定其网络的重要度，结合上述两个指标最终得出节点在整个通信时段的重要度。该方法是对传统仅考虑网络结构评估节点重要程度的一种改进，增加了通信时段的重要程度，使评估结果更加真实。

1 通信网络节点重要度评估方法

通信网络的链路连接情况可用有向图G=(V,E)表示，其中V为节点，代表信息收发处理终端，E为边，代表各终端的连接关系，并且约定任意两个节点之间只有一条连边，且不存在自环。同时注意到通信网络是动态变化的网络，不断有节点接入和退出，导致网络的拓扑结构不断变化。因此在分析通信网络节点重要度时，首先从网络拓扑结构入手，研究在某一时段稳定的通信网络各节点的重要度，再评估该时段通信网络在整个通信时段的重要度，最后聚合得出全部通信节点在整个通信时段的重要度。通信网络节点重要度的评估模型为：

其中gi为节点i在整个通信时段的重要度，hki为在第k时段的通信网络中节点i的重要度，wk为k时段的通信网络在整个通信时段的重要度，下面分别建立hki、wk的评估模型。

2 复杂网络节点重要度评估模型

建立hki的评估模型时借鉴复杂网络的传播机制，首先根据节点的实时负载和容量确定节点的实时状态，再根据节点实时状态建立节点失效后向临近节点重分配负载的模型，最后根据节点负载重分配对临近节点的震荡程度评估节点的重要度。

2.1 节点状态

节点状态由可用节点能够容纳转移负载的能力来表示，它由两个方面的因素决定: 一是节点自身的负载剩余容纳能力，二是相邻节点的负载剩余容纳能力。从上述描述的过程来看，它可以分为两个阶段，首先考虑节点剩余容纳能力，假设节点i的实时负载为Qi，节点的容量为Ci，那么节点的负载剩余容纳能力Ri可表示为：

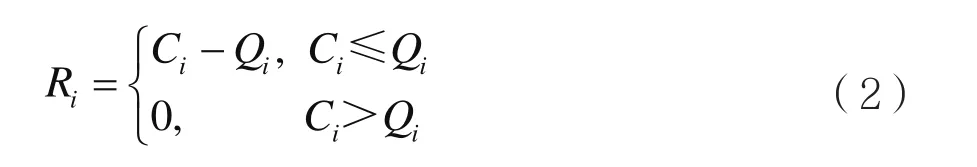
即节点负载剩余容纳能力为节点容量与现有负载的差值，当负载超过容量时，其负载剩余容纳能力为0，此时该节点已经失效。节点负载剩余容纳能力体现的是节点还能够处理或者容纳负载的能力，Ri值越大说明其处理能力越强，在负载重分配时应该占有优势，其分配的比例应该越高，反之则越低，它是随着节点负载的变化而不断变化的。

考虑到相邻节点负载剩余容纳能力的影响，提出能够更精确衡量节点负载剩余容纳能力的节点状态，该状态是节点自身的负载剩余容纳能力与相邻节点负载剩余容纳能力的有机结合，共同构成了节点真实的负载剩余容纳能力。对节点状态的指标进行定义，如式（3）所示：

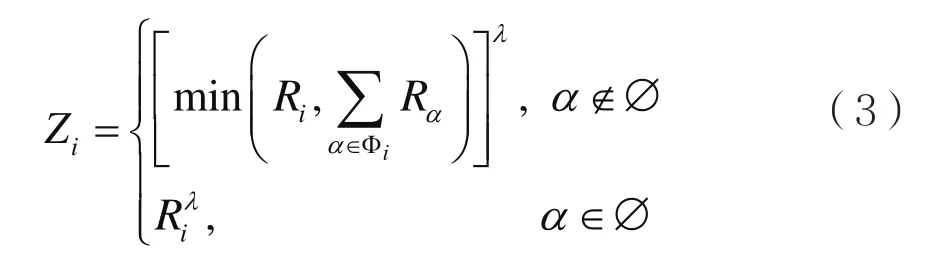
其中：Zi表示节点状态；Ri表示节点裕度；Φi表示节点i的邻接节点；λ为权重参数，通过调节λ的值可以调节整个节点状态在负载重分配时所占的比例，当时λ=0式（3）为局部负载均匀重分配。式（3）反映的是节点能够容纳负载的能力，它取自身节点负载剩余容纳能力与相邻节点负载剩余容纳能力总和中的最小值，当没有相邻节点时，节点负载剩余容纳能力即为自身的节点负载剩余容纳能力。

2.2 负载重分配

负载重分配方式是描述节点失效后其上的负载向网络中其他节点进行转移的规则。负载重分配方式如图1所示，节点失效后，原本通过该节点的负载信息流将会重新选择通过路径，其上的负载将会转移到与之相邻的节点，以保证整个网络的有效运行，整个网络会由于节点的失效而进行负载的全面更新，即Qi´=Qi+ΔQi，i∈Φf其中Qi为更新之前的负载，Qi´为更新之后的负载，ΔQi为更新时的增量，Φf为失效节点f的所有邻接节点。

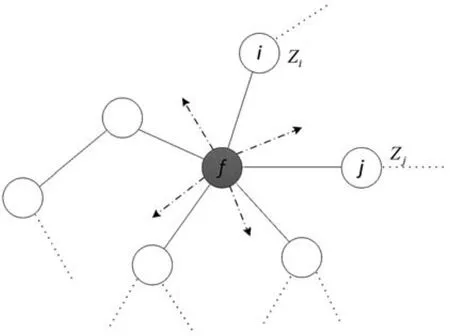
图1 基于节点状态演化的负载重分配方式

假设失效节点f的负载为Qf，相邻节点的节点状态为Zi，在相邻节点上重新分配的负载增量可以用式（4）表示，它是对经典近邻重分配方式的改进，它与节点状态相关而不与节点负载相关。

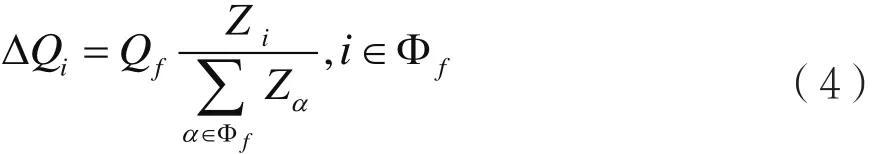
2.3 节点重要度评估

依据上述负载重分配模型，参照文献[8］提出的节点重要度评估指标，可以用节点f故障后由于其自身负载向近邻节点转移而引起近邻节点向失效状态转移的程度来衡量节点引发网络级联故障的能力即节点的重要度。为了避免触发进一步的级联故障发生，节点i经重分配后的负载受到其容量Ci的限制，Ci=(1+η)Q0i其中常数η为网络的最大忍受度，表示处理额外负荷的能力，Q0i为节点初始负载，因此重分配的负载将满足式（5）。

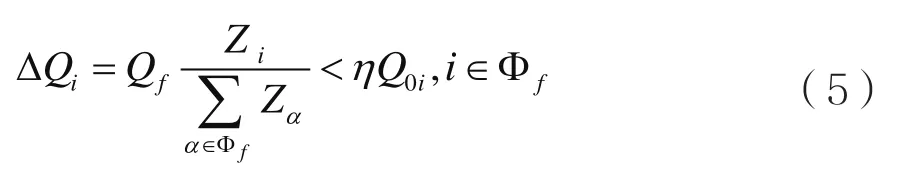
其中，|Φf|为故障节点的所有近邻节点数目。

3 通信网络重要度评估模型

从时域的角度出发，某一拓扑结构通信网络的重要度主要取决于以下两点，一是该网络所处的时间段在整个通信时段中的重要程度，如军事通信中发起进攻阶段的通信网络要比预先侦察阶段的通信网络重要；二是该网络相对整个通信时段占据的时长比例，如在通信网络中经常活跃的节点所承担的信息处理任务较多，由这些节点构成的网络重要度较高，而活跃度较低的节点往往是备用节点或偏远节点，其重要度相对不高。以上述理论为依据提出通信网络重要度评估模型，将通信时段划分成不重叠的若干个时间片[9］，在每个时间片内通信网络的拓扑结构不变，则将时段内变化的通信网络分解成基于多个时间片的静态通信网络，每个时间片对应一个静态的通信网络结构，且不同于前一时间片或后一时间片对应的静态通信网络结构，建立起时间片与某一拓扑结构通信网络的对应关系，并以时间片在通信时段内的重要度和相对时长作为片上通信网络的重要度。

根据上述思路建立通信网络重要度评估模型。首先将整个通信时间段U划分为L个不重叠的时间片，得{[b1,e1］;[b2,e2］;…;[bL,eL］}，其中b表示时间片开始时刻，e表示时间片结束时刻。再由通信决策者将整个通信时段划分为N个子段{[T1,T2］;[T2,T3］;…;[TN,TN+1］}，并根据子段在整个通信时间段上的位置，以及该子段所承载的通信任务等，采用专家打分的方法确定各子段的重要度为 {θ1;θ2;……;θN}，且如图2所示。则时间片k的重要度rk的计算模型为：

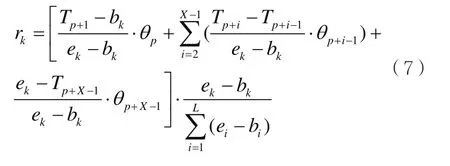
其中Tp≤bk＜Tp+1，Tp+X-1≤ek＜Tp+X，再进行归一化处理得出时间片k对应的通信网络重要度为

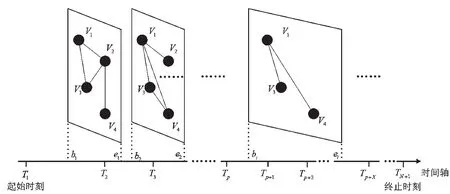
图2 不同时间片对应的通信网络示意图

4 网络的构建及节点重要性评估仿真实验

4.1 通信网络构建

本文在构建实例分析所需的通信网络时主要考虑到通信网络的以下两个特点，一是网络的时变性，不断有新节点接入和老节点退出；二是新节点往往选择度值较大的数个老节点建立连接，退出的多是度值较低的节点。因此本文提出一种时变的随机网络模型，该模型的算法如下：

Step 1初始设定：首先建立一个具有j0个节点，链路节点比为S0的随机网络，并为每个节点按照1至j0编号。

Step 2增长节点：每间隔B时间增加一个新节点O，在原节点最大编号上加1作为新节点的编号，并引出m≤j0条边与之前网络的m个节点相连，其中B～N(B0,σ21)，m～N(m0,σ22)。

Step 3择优连接：连接节点的选择按照度值优先原则进行，选择老节点i作为新边连接节点的概率为:其中D(·)为节点度值。

Step 4退出节点：选择度值最小的节点退出网络，若度值最小的节点有多个则随机选择一个，节点退出后与其相连的链路全部断开。

Step 5通信子段重要度赋值：真实情况下通信子段应由决策者考虑主观判断、客观实际进行划分并赋予重要度，通常靠近整个时段中间的子段承担较多的信息传递任务，相应的重要度较高，两边的子段重要度逐渐降低。仿真中为简化该过程，将整个通信时段均匀划分为N个子段{[T1,T2］;[T2,T3］;…;[TN,TN+1］}，并用正太分布近似为各子段赋予重要度，则第i个子段的重要度为：

4.2 实例分析

取上述时变随机网络模型中的参数j0=200，S0=3，B0=100s，m0=3，σ1=10s，σ2=1，σ3=60s，N=6，T1=0s，TN+1=3 600s，并设定每个节点的初始负载为Q0i=akγi，ki为节点的度a、γ为可调节参数控制初始负载的大小，为简化计算所有节点的a=1，γ=1，节点容量模型中η=0.07。基于前述的节点重要度评价方法，排序结果见表1，表1仅展示排序前30位的节点。

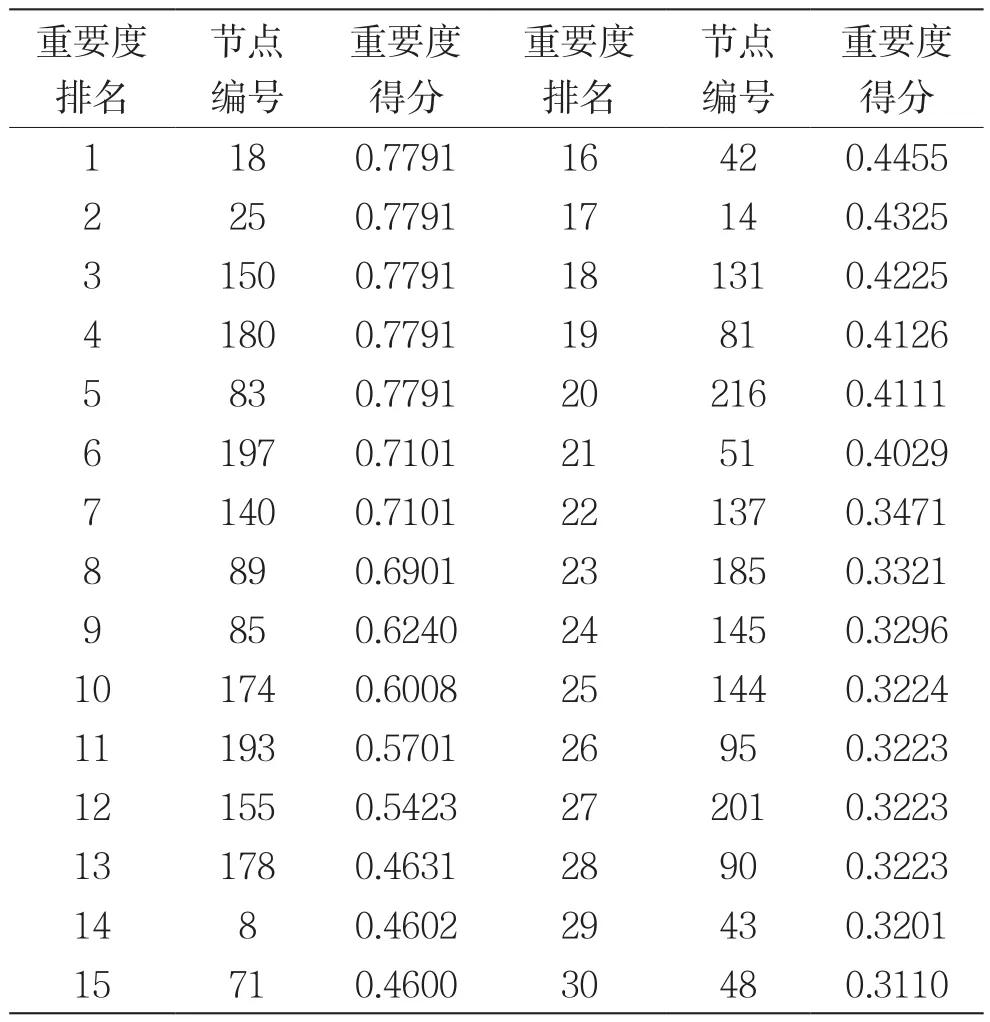
表1 各时间片内节点重要度

根据节点重要度排序结果，按照节点重要度从高到低依次从网络中使该节点失效，并提出以失效影响度Ω(i)作为指标，评估节点i失效后对整个通信时段网络的影响程度，网络失效结果如图3所示。

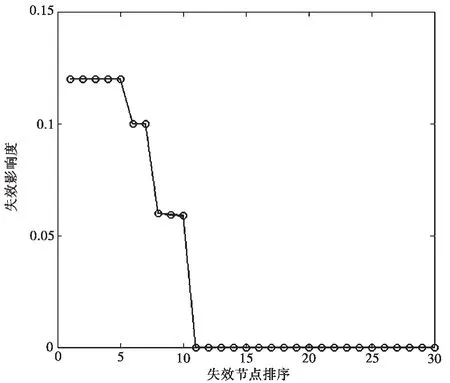
图3 通信网络失效效果

其中失效影响度的定义式如式（9）所示：

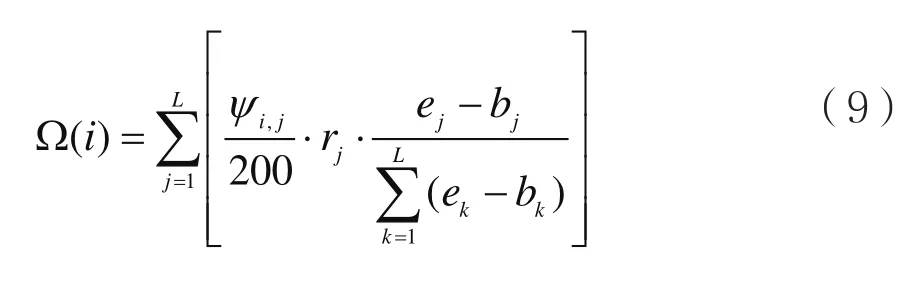
其中ψi,j/200表示在时间片j对应的网络上节点i失效后所级联失效的节点数量比例。该式综合考虑了节点失效后在单个时间片上照成的影响，时间片在整个通信时段的重要性以及影响持续的时间，较为真实的反映节点失效后对整个通信的影响程度。

图3中的横坐标为按照节点重要度排序的结果，从1到30依次失效，纵坐标表示失效影响度。从图中可以看出排序靠前的节点失效所引起的影响要明显大于排序靠后的节点。对于该通信网络来说，此排序结果的失效效果很好，排序最靠前的10个节点，均表现出来在此网络参数和节点参数下的良好失效效果; 而排序靠后的其余节点失效效果较差。以此证明，对于这种网络拓扑结构，本文的排序方法较为适合。

5 结 语

本文提出的通信网络节点重要程度评估模型，在传统评估模型的基础上，考虑了不同通信时段重要程度及时长对节点重要程度的影响，同时兼顾考虑了节点在网络拓扑结构中位置重要程度，节点在网络传播中的重要程度，相对较为真实的定量反映节点的重要度，为通信网络关键节点的发现和保护提供一定帮助。但是在评估模型中对各节点的功能和业务并未进行区分，这将是下一步研究的重点。