正交多进制扩频的二元软信息提取方法*

牛桂兵

（中国电子科技集团公司第五十四研究所，河北 石家庄 050081）

0 引 言

正交多进制扩频传输是一种M进制正交调制技术，兼顾了扩频处理增益和传输容量，还具有较好的接收机性能，在一定信号带宽限制下能够获得更高的信息传输速率[1］。根据数字通信原理，M进制正交传输波形能够获得更低的解调门限。当M=16时，在BER=1E-6下，它较BPSK/QPSK调制的解调门限低约4 dB[2］。若再进行纠错编码，则接收门限将会更低，换言之会得到更好的传输性能。另外，多进制扩频还能获得较好的抗多径能力[3］，因此各种正交码的扩频传输技术在多个领域获得了应用，如无线抄表、无线光通信[4］和水声通信[5］。近几十年来，纠错编码技术获得了快速发展。软译码是主流的译码方法，较硬译码能获得不少于2 dB的性能提升[6］，从而进一步改善传输性能。在通信工程开发资源市场上，纠错编译码模块作为独立可运行的一种产品进行销售，一般提供二元软信息接口与解调器连接使用，使得解调器与译码器各自独立工作，且纠错编译码模块更加通用，因此有必要探讨传输波形的二元软信息提取方法。

1 二元软信息提取

1.1 一般的软信息提取原理

主流的传输系统构造方法如图1所示[7］。在接收端，译码模块与解调模块分开，各自独立工作；接收信号解调后不进行判决，而是提取出二元软信息输出给软译码器进行译码，然后判决输出。

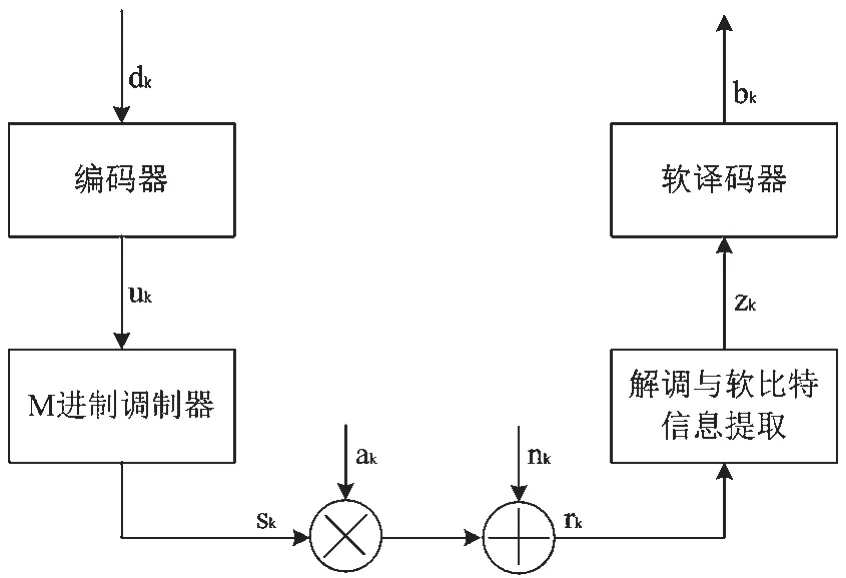
图1 传输系统一般构成模型

依据一般的软信息提取原则，就是获得接收信号矢量与参考波形的距离，而距离的远近等效于判决为参考波形的概率大小。对于M进制而言，参考波形有M个，每个接收符号有n个比特，表示为b0,b1,…,bn。解调器需要提取出n个比特的软信息作为软译码器的输入，那么就需要对接收信号矢量反映射到n个比特的软信息。以b0为例，说明其软信息提取方法如下：

（1）将所有b0=0的参考波形分为一组，所有b0=1的参考波形分为另一组；

（2）计算当前接收信号与b0=0组中所有参考波形的距离，找到距离最近者称作D0；

（3）计算当前接收信号与b0=1组中所有参考波形的距离，找到距离最近者称作D1；

（4）D0-D1就是b0的软信息，小于0表示b0=0的概率大，反之表示b0=1的概率大。

按照上述方法依次取得同一个符号中其他比特的软信息，作为软译码器的输入。

1.2 正交多进制扩频的二元软信息提取

结合纠错编码的M进制正交多进制扩频的接收机结构如图2所示。

图2 结合纠错编码的M进制正交扩频接收机结构

信号的解调是将接收矢量与M个本地参考波形进行匹配，产生M个匹配值，此为解调；若没有纠错编码，则选择其中最大者完成符号映射，此为判决，如：

式中sm为本地参考波形。然后，并串变换输出码流，接收处理过程结束。当引入纠错编码后，解调器后应连接二元译码器，而解调器应输出各比特的二元软信息给译码器。

以下以M=16为例进行详细说明。

M进制正交扩频的波形可以采用众所周知的Hadamard矩阵构造，在此不进行展开，以S1,S2,…,S16表示，比特映射关系见表1。在此仅论述其接收端的处理。

单因素方差分析结果显示，5组样本经不同方法再矿化处理后，釉质表面钙磷比总体有明显差异(F=132.630，P=0.000)；钙磷比由高到低分别为碳酸氢钠液组(D组)>绿茶浸提液组(C组)>多乐氟组(E组)>奥威尔组(B组)>人工唾液组(A组)(表1)。两两比较显示，除绿茶浸提液组与碳酸氢钠液组的钙磷比无统计学差异(P=0.450)外，其他各组釉质表面钙磷比两两相比均有统计学差异(P<0.05)。

表1 M=16进制正交扩频波形与比特对应关系

接收机处理过程如下。

（1）参考点构造

无噪条件下，接收矢量与所有可能的16个本地参考波形的相关计算值，分别为R1、R2、R3、R4、R5、R6、R7、R8、R9、R10、R11、R12、R13、R14、R15、R16。在接收信号归一化处理后，无噪相关结果值均为16，在此记为Vref=16。

（2）解调

接收信号矢量r与所有参考波形进行相关运算，结果为Rm（1≤m≤16）：

Rm与无噪相关结果Dref相减取绝对值，该值表示解调结果与参考值的距离。

（4）二元软信息提取

因为引入了纠错编码，为发挥软译码的性能优势，对相关运算结果不能进行判决，而是对16个相关运算结果进行处理，提取出每比特对应的软信息作为软译码器的输入。

二元输入译码器需要的软信息实质是能够表征接收矢量所传输原始符号中对应比特与-1或1的距离。根据表1比特与波形的对应关系，b0=0的波形序号分别为1、3、5、7、9、11、13、15，选择其对应距离Dm的最小值，b0=1的波形序号分别为2、4、6、8、10、12、14、16，选择其对应距离Dm最小值，二者再相减作为b0的软信息。在距b0=0波形距离大于距b0=1波形距离时，b0为“1”的概率大，该信息为正；在距b0=0波形距离小于距b0=1波形距离时，b0为“0”的概率大，该信息为负。该逻辑与二元软译码逻辑相符。

b0的软信息计算表达式如下：

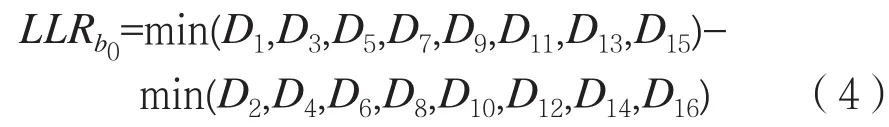
同理，参考表1给出的波形与比特映射关系，分别给出b1、b2和b3的软信息计算表达式：

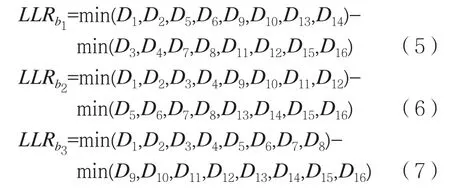
2 性能验证

为验证第2章节提出方法的有效性，进行如下仿真。仿真条件：M=16，过采样系数OVR=4，滚降因子β=0.3，编码方式turbo码，码率R=1/2，码长8 320 bit，信道模型为高斯加性噪声信道。

进行比较的调制方式有：（1）无纠错QPSK调制；（2）QPSK进行turbo编译码，码率1/2；（3）无纠错编码的M=16正交多进制扩频；（4）M=16正交多进制扩频进行turbo编译码，码率1/2。

从图3可以看出，M=16的多进制正交扩频传输在使用本文提出的方法提取软信息后，跟随软译码处理，在BER=1E-6误码率下，较非纠错编码系统获得接近4.3 dB的编码增益。相同仿真条件下，QPSK采用同样纠错编码后，在BER=1E-6误码率下，获得了约5 dB的编码增益，略优于正交多进制扩频进行相同纠错处理获得的误码改善。可见，仿真结果表明本文所提方法能够较准确地提取出接收信号的软信息，发挥纠错编码的纠错能力。图3中的M16无纠错性能曲线与文献[8］的仿真结果相同，也可以说明本文所进行的仿真验证方法是可信的。

图3 误码性能

3 结 语

以上论述以M=16为例进行，方法对M为其他值时依然有效。事实上，M进制正交扩频可选择更长的码及更多的波形，从中选择部分波形用于传输，从而获得更好的扩频处理增益，收到一定对抗干扰的效果。另外，还能够降低符号速率，简化多径信道下的接收处理[9］。结合纠错编码后，接收性能有明显提高，在对接收门限敏感的应用场合具有一定的实用价值。同时，本文提出的软信息提取方法无需信噪比信息，实现简单。另外，本文提出的软信息提取方法与所采用的纠错编码技术无关，可与任意二元软信息输入的译码器结合使用，具有较好的灵活性。