无时限信号通过LTI系统的间接复频域分析方法*

陈绍荣 ，何 健 ，薛在阳 ，陈柏良

（1.陆军工程大学通信士官学校，重庆 400035；2.军委装备发展部军事代表局驻成都地区军事代表室，四川 成都 610041；3.奥特斯科技（重庆）有限公司，重庆 401133；4.深圳市惟新科技股份有限公司，广州 深圳 518000）

0 引 言

在国内外《信号与系统》著作[1-2］中，均提到了连续时间直流信号、符号函数、抽样信号、无时限复指数信号和周期信号的双边拉普拉斯变换不存在。因此，这些信号通过LTI因果系统时，不能采用复频域分析法求解系统的零状态响应。本文在著作[3］的基础上，借助信号分解的概念，首先将这些信号分解成反因果信号和因果信号之和，再利用LTI因果稳定系统响应的可加性求解系统的零状态响应。

1 无时限复指数信号通过LTI因果系统的间接复频域分析方法

1.1 LTI因果系统零状态响应的复频域表示式

设n阶LTI因果系统的转移函数为：

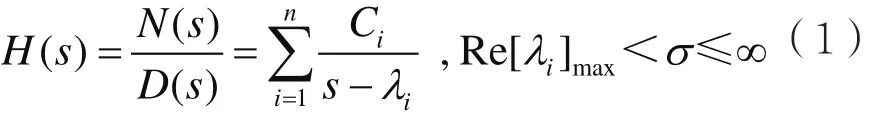
式中，λi(i=1,2,…,n)为LTI因果系统的特征根。

设激励f(t)=Aewt，其中A为常数，w为复变量，且满足主导条件 Re[w］＞Re[λi］max(i=1,2,…,n)。

无时限复指数信号f(t)=Aewt可写成：

式中，ε(t)为单位阶跃信号。

考虑到式（2），则LTI因果系统的零状态响应可以表示为：

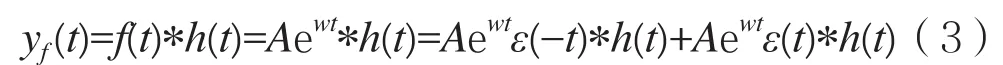
由于：

因此，对式（3）两边取双边LT，结合式（4）和式（5），LTI因果系统的零状态响应的复频域表示式为：

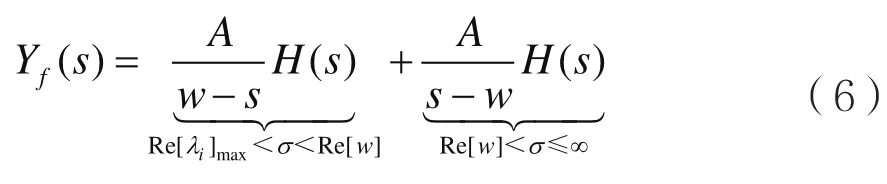
式（6）是间接利用复频域分析法求解无时限复指数信号通过LTI因果系统时的零状态响应的依据。

1.2 无时限复指数信号通过LTI因果系统的间接复频域分析方法举例

例1：设一阶LTI因果系统的单位冲激响应为h(t)=e-tε(t)， 激 励f1(t)=5etcost，f2(t)=5etsint， 试 分 别求系统的零状态响应yf1(t)和yf2(t)。

解：考虑到h(t)=e-tε(t)，则有：

假设f(t)=5e(1+j)t，考虑式（7），由式（6）可得：

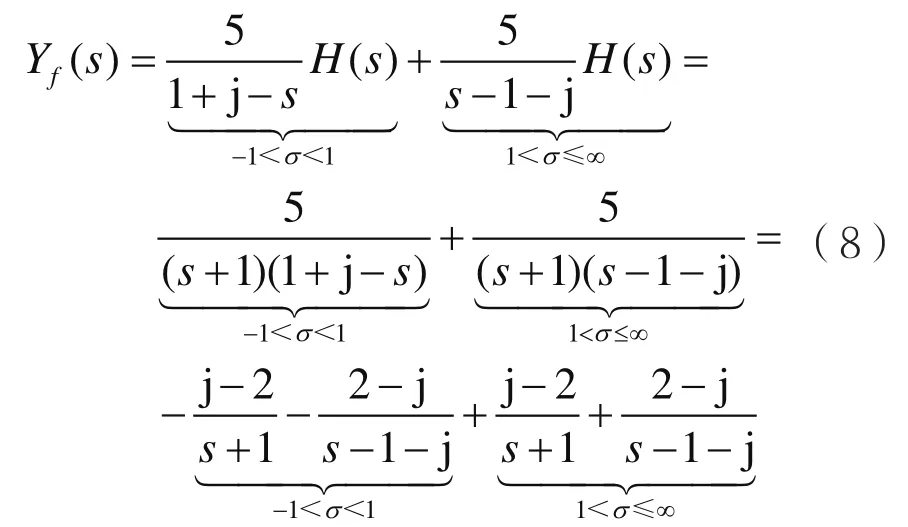
对式（8）两边取ILT，可得：

即：

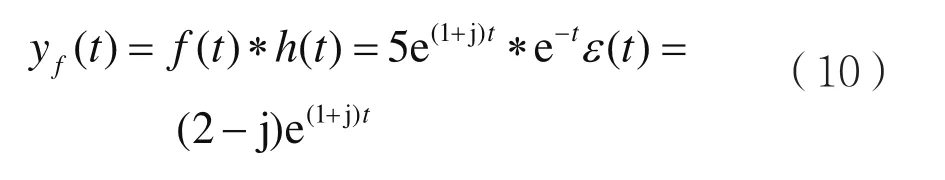
由式（10）可知，LTI因果系统的零状态响应分别为：

2 等效Jordan引理

设λi(i=1,2,…)为F(s)在s平面虚轴上的极点，以为半径，在s平面上画出半径为R1,R2,…,Rn,…的不连续圆周序列CR1,CR2,…,CRn,…。在CRn上，复变量s=sn=Rnejθ，复数列为F(sn)，显然若圆周序列CRn与布拉米奇路径σ0±j∞分别交于A、C两点，CABC是CRn上逆时针方向的一段弧，CADC是CRn上顺时针方向的一段弧，如图1所示。

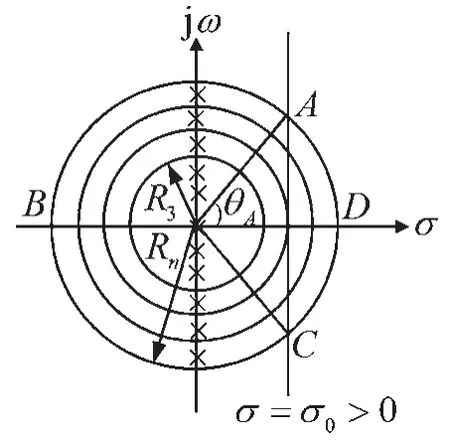
图1 等效Jordan引理的圆周序列示意

2.1 等效Jordan引理的内容

在圆周序列CRn上，若函数F(s)连续，且复数列F(sn)满足条件：

不论布拉米奇路径σ0±j∞位于s平面的左半平面σ0＜0，还是位于s平面的右半平面σ0＞0，均可以得到下述结论。

当t＞0时，有：

当t＜0时，有：

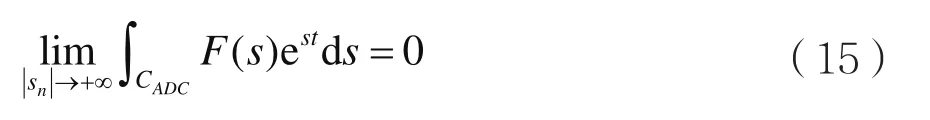
2.2 利用等效Jordan引理及留数定理计算ILT

2.2.1 象函数F(s)的收敛域属于0＜σ＜β的情形

在s平面的右半平面上，作布拉米奇路径σ=σ0±j∞（其中，0＜σ0＜β）。在圆周CRn上，若函数F(s)连续，且复数列F(sn)满足等效Jordan引理的条件式（13），考虑式（14）和式（15），则有：

式中，λl(l=0,±1,±2,…)是象函数F(s)的第l个区左极点（Re[λl］≤ 0 的极点），λ´r(r=1,2,…,p2)是象函数F(s)的第r个区右极点（Re[λ´r］≥β的极点）；第二部分的负号是由于围线的绕行方向为负向（即顺时针方向）。

2.2.2 象函数F(s)的收敛域属于α＜σ＜0的情形

在s平面的左半平面上，作布拉米奇路径σ=σ0±j∞（其中，α＜σ0＜0）。在圆周CRn上，若函数F(s)连续，且复数列F(sn)满足等效Jordan引理的条件式（13），考虑式（14）和式（15），则有：

式中，λl(l=1,2,…,p1)是象函数F(s)的第l个区左极点（Re[λl］≤α的极点），λ´r(r=0,±1,±2,…)是象函数F(s)的第r个区右极点（Re[λ´r］≥0的极点）；第二部分的负号是由于围线的绕行方向为负向（即顺时针方向）。

3 周期信号通过LTI因果稳定系统的间接复频域分析方法

3.1 LTI因果稳定系统零状态响应的复频域表示式

设n阶LTI因果稳定系统的转移函数为：

式中，λi(i=1,2,…,n)为LTI因果稳定系统的特征根，且 Re[λi］max＜0(i=1,2,…,n)。

设f0(t)是时限于区间t∈[0,T0］的时限信号，即满足：

式中，ε(t)为单位阶跃信号。

显然，时限信号f0(t)的双边LT的收敛域为有限全s平面，即：

又设：

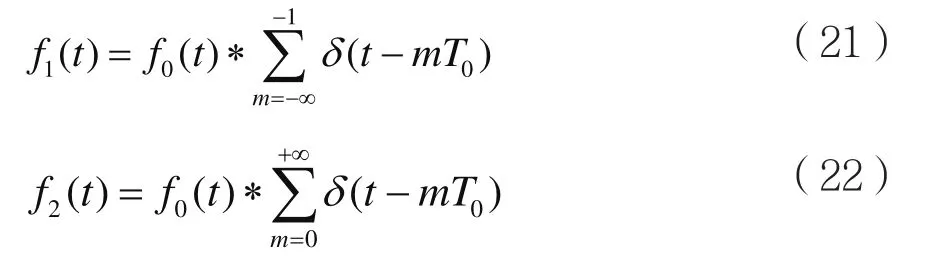
则周期为T0的周期信号fT0(t)可表示为：

对式（21）两边取双边LT，并考虑到式（20），则有：

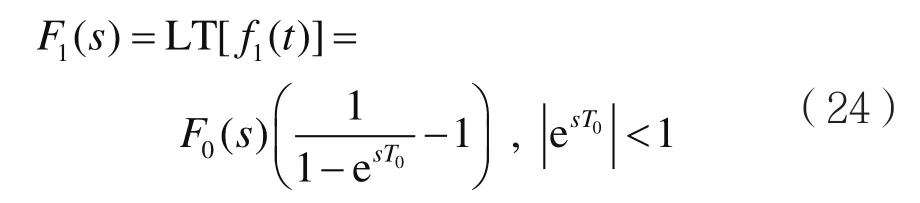
式（24）又可以表示为：

对式（22）两边取双边LT，考虑式（20），则有：

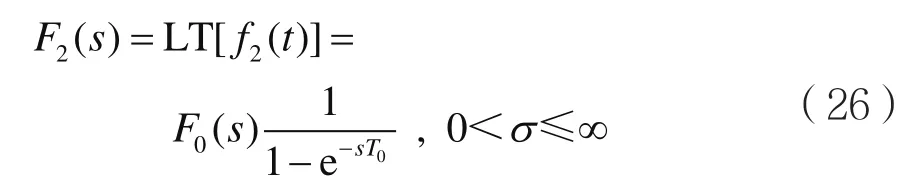
考虑到式（23），则LTI因果系统的零状态响应可以表示为：

对式（27）两边取双边LT，结合式（25）和式（26），则LTI因果稳定系统的零状态响应的复频域表示式为：

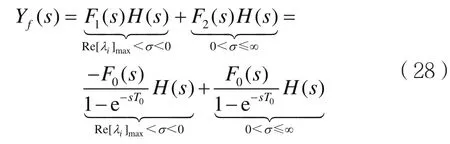
式（28）是间接利用复频域分析法求解周期信号通过LTI因果稳定系统时的零状态响应的依据。

3.2 周期信号通过LTI因果稳定系统的间接复频域分析方法举例

解：考虑到f0(t)=ε(t)-ε(t-1)，则有：

考虑到h(t)=ε(t)-ε(t-1)，则有：

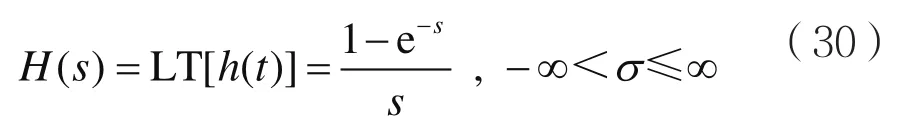
考虑到式（29）和式（30），由式（28）可得：

由式（31）可知，s=0是Yf(s)的二阶极点；令1+e-s=0，即 es=ej(2n-1)π，得Yf(s)的一阶极点λl=j(2l-1)π(l=0,±1,±2,…)。

由于式（31）中的两项分别都满足等效Jordan引理条件式（13），因此对式（31）两边取ILT，并考虑式（16）和式（17），可得系统的零状态响应：

式（32）正是高度1、宽度为2、周期为2的周期三角波信号三角函数形式的傅里叶级数展开式。

4 结 语

本文借助信号分解的概念，将无时限复指数信号或周期信号分解为反因果信号和因果信号之和，利用LTI因果稳定系统响应的可加性，给出了一种求解系统零状态响应的间接复频域分析方法。