基于M-ELM的大坝变形安全监控模型
胡德秀,屈旭东,杨 杰,程 琳,常 梦
(1.西安理工大学 水利水电学院,陕西 西安 710048; 2.中国水电建设集团十五工程局有限公司,陕西 西安 710016)
水利工程在其服役过程中不仅要承受各种动、静循环荷载及各种突发性灾害的作用,还要承受来自恶劣环境的侵蚀与腐蚀,导致结构服役期间局部和整体安全性能随着时间推移而逐步衰退,因此及时准确地了解各水工建筑物的工作性态以确保其安全极为重要[1]。依据水利工程原型监测资料,应用统计数学、工程力学、信息科学等方法建立安全监控模型对影响水利工程的各因素(特别是时效分量)进行物理解释,定量分析评价和馈控水利工程的安全状况,揭示建筑物的异常服役性态,是保障工程安全的重要手段[2]。
目前,具有代表性的大坝变形安全监测资料分析模型主要有4种:统计模型、确定性模型、混合模型及组合模型,其中统计模型和确定性模型为技术支撑主体[3]。
统计模型[4-7]是指以概率论和数理统计理论为技术支撑对监测数据进行建模分析,建立荷载集与荷载效应集之间的关系的表达式。其中最常用的是静水压力分量-温度周期分量-时间分量(hydrostatic-seasonal-time,HST)方法,但其只考虑了静水荷载的可逆效应、温度周期荷载的可逆效应和时效不可逆效应。统计模型的缺点主要表现在:①对大坝的工作性态不能从力学概念上加以本质解释;②统计模型基于各变量相互独立的假设条件,未考虑因子之间的相关性,可能会导致分离变量失真;③模型不能反映变量之间的非线性关系。
确定性模型[8-11]采用有限元法计算荷载(如水压、温度等)作用下大坝和坝基的效应场(如位移、应力场、渗流场等),然后与实测值进行优化拟合,以求得调整参数(因为大坝与坝基的平均物理力学参数、渗流参数及边界条件等的不确定性),从而建立基于物理力学本质的表达式。确定性模型的缺点主要表现在:①大坝及坝基材料参数的不确定性;②边界条件设置的不确切性;③模型简化的不精确性。
混合模型[12-14]采用有限元法计算水压分量,其他分量采用统计模型,然后与实测值进行优化拟合。混合模型虽然从力学概念出发,提高了模型计算精度,但同时也继承了统计模型和确定性模型的固有缺陷和假设。
组合模型[15-16]通过整合各子模型的应用条件、构模机理和出发点等多种有用信息,将多个单一模型进行非线性优化组合,达到对映射关系更加合理和全面的刻画,有效地提高拟合和预测精度,建立性能更佳的监控模型。组合模型的缺点主要表现在:①线性组合模型应对非线性问题时有可能得到不符合实际的负权重;②组合函数构造十分困难。
近年来,随着大坝安全监控、计算机、大数据、人工智能等理论与技术的发展,越来越多的数据挖掘方法被应用到水利工程安全监控建模中来,涌现出了许多智能算法监控模型[17-20],在解决监控模型因子不确定性和非线性问题、预测精度及泛化性等方面表现出了特有的优势。
针对以往监控模型预测精度低、鲁棒性差及泛化能力弱的不足,鉴于智能算法优越的数据处理能力,本文引入机器学习浅层结构算法中的极限学习机(extreme learning machine,ELM)方法以解决大坝变形监测数据存在的因子不确定性和非线性问题。同时,针对传统监控模型抗粗差能力差等问题,引入稳健估计理论,建立了基于稳健估计极限学习机(M-ELM)的大坝变形安全监控模型,强化了模型的鲁棒性,提高了模型的预测精度及泛化性,更加接近真实地反映大坝的工作性态。
1 ELM原理
ELM是一种新型单隐含层前馈神经网络学习算法[21]。传统的神经网络学习算法(如BP算法)需要人为设置大量网络训练参数(权值、偏置及学习率等指标),并且很容易产生迭代次数过多、学习时间长及局部最优解等问题。相对于传统的神经网络学习算法,ELM在算法执行过程中不需要调整网络的输入权值和偏置,只需要进行隐含层节点数的设置,并且产生唯一的最优解,在保证网络具有良好泛化性的同时,极大地提高了学习速度,广泛地被用于各种数据处理中[22-23]。图1为ELM网络结构图。

图1 ELM网络结构
为了在因子比较和评价的指标处理中去除数据的量纲限制,将数据进行标准化(无量纲化)处理,以便于不同单位或量级的指标能够进行比较和加权。对于n个经标准化处理的数据样本(xi,yi),其中xi=(xi1,xi1,…,xip)T为自变量样本,yi=(yi1,yi1,…,yik)T为因变量样本,对采用l个隐含层节点的单隐含层神经网络,设权值为ωi,偏置为bi,其描述可以表示为以下方程组形式:
Hp×lβl×k=yp×k
(1)

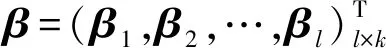
传统极限学习机隐含层节点输出权重采用最小二乘法进行计算,构建的损失函数为
(2)

(3)
式中:Η+为Η的Moore-Penrose广义逆。
传统的ELM算法的输出权重的计算采用经典的最小二乘法,当网络隐含层输出数据误差服从正态分布情况时,最小二乘估计具有最优统计性质,但实际情况往往不是这样,其对于粗差的抵抗性特别差,当输出数据存在多重共线性或粗差时就会对参数的估值产生较大的影响,计算结果也会产生严重的偏差,甚至得出错误的结论,严重影响网络训练的精度。同时,隐含层参数的选取均采用随机生成的方法,致使每一次训练和测试结果存在一定的随机性,对于网络的稳定性产生不利的影响。因此从网络学习的精度和稳健性方面考虑,ELM算法仍有两个需要解决的固有缺陷:隐含层参数的随机选取会造成ELM网络训练结果有较大的不稳定性;如果训练数据存在共线性或粗差干扰,输出层权值的最小二乘法估计结果会很差[25]。
2 M-ELM大坝变形安全监控模型
水利枢纽工程中往往建有各类型的大坝、溢洪道、隧洞等建筑物,建筑物的安全是其挡水、泄水、放水等功能发挥的关键。为此,通过监测各种水工建筑物变形、渗流、应力等安全项目,实时监测工程安全。如何利用实测数据进行建模拟合预测分析是实现水利工程安全监控的核心基础。

(4)
式中:ρ为影响函数;N为样本总数。当损失函数Q′取最小值时可得出隐含层权值的最优解。

(5)
则可以将式(4)转化为
(6)

(7)

(8)
法方程矩阵表达式为
XTWXβ=XTWy
(9)
故稳健估计极限学习机的计算结果为
(10)
M-ELM大坝变形安全监控模型建模流程见图2,建模步骤具体如下:
a. 选取实测监测资料作为模型训练样本和测试样本,将所有数据进行标准化,并将标准化样本数据输入到监控模型。
b. 通过试验确定隐含层节点个数,并随机选取网络参数wi、bi,选择某一无限可微函数(如S形函数、正弦函数和复合函数等)作为隐含层神经元激活函数,计算隐含层节点输出矩阵H。
c. 根据计算的隐含层节点输出矩阵H,利用稳健估计理论计算隐含层节点输出权重βi,并进行输出节点值的计算,即为监控模型的拟合值,同时进行训练样本均方差的计算,即为训练误差。
d. 根据训练样本训练出的隐含层节点输出权重进行测试样本的预测值计算,即为监控模型的预测值,同时计算出预测值与测试样本之间的均方差,即为测试误差或预测误差。
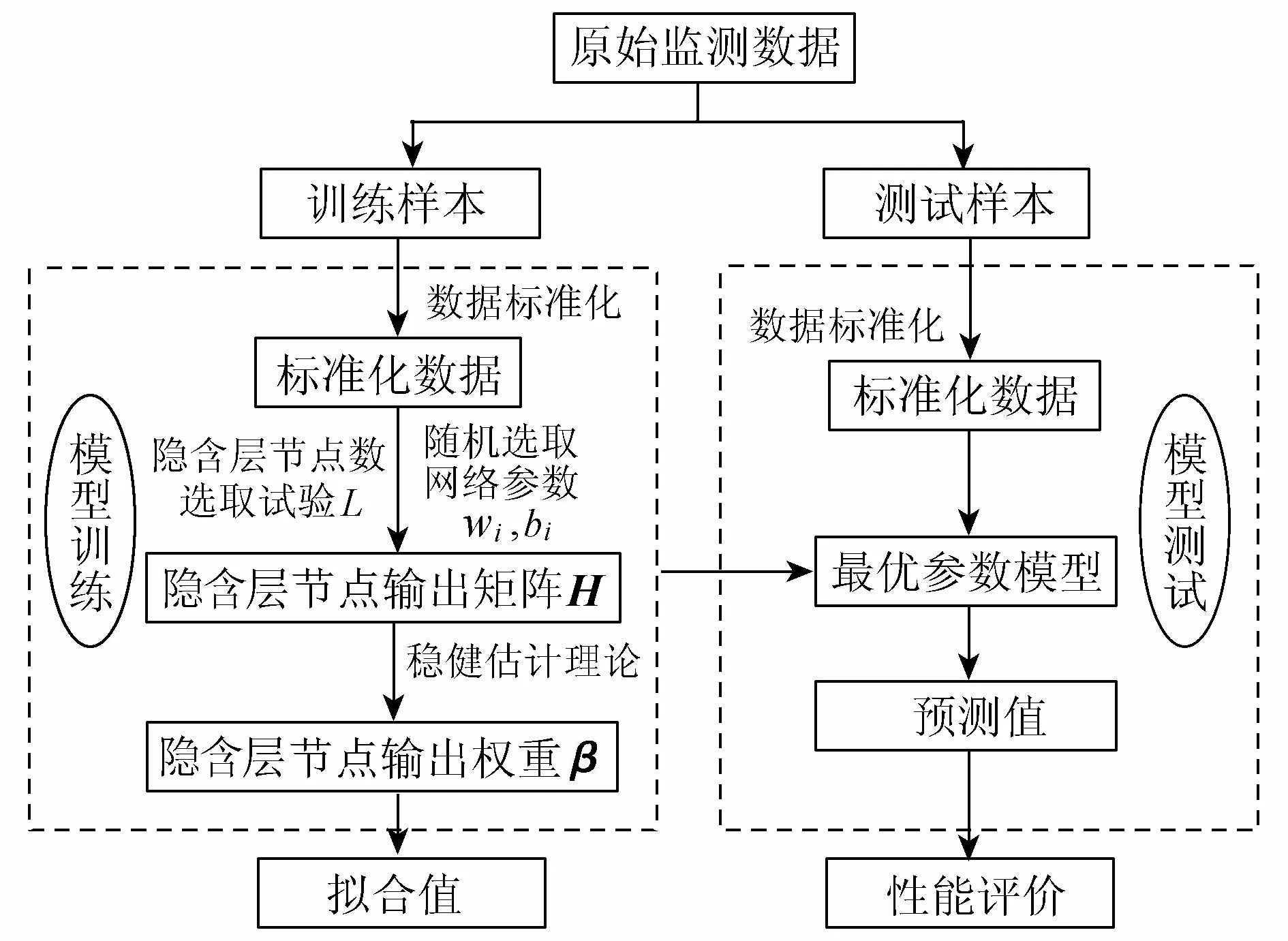
图2 M-ELM大坝变形安全监控模型建模流程
3 模型验证
3.1 工程简介
以某水利枢纽工程监测数据为例进行M-ELM大坝变形安全监控模型的应用研究。该工程大坝为壤土心墙土石坝,最大坝高101.8 m,坝顶长度297.36 m。大坝采用5个纵断面共30个测点监测大坝的水平位移。选取该大坝高程为691 m的马道旁D7测点2010年1月至2014年5月共178个样本的监测资料,主要包括该测点水平位移(向左岸为正,向右岸为负)、水库大坝上下游水位及坝址区温度等。
3.2 分析结果及对比
由于土石坝工作性态异常复杂,影响其变形的因素有坝型、剖面尺寸、筑坝材料、施工程序及质量、坝基的地形、水库水位的变化情况等。因此本文在土石坝变形监测量的统计模型选择中,选取水位因子、温度因子及时效因子作为模型主要影响因素,构建如下土石坝水平位移的统计模型:

(11)
式中:b0为常数项;a1i、a2i分别为上、下游因子回归系数;b1、b1i、b2i为温度因子回归系数;c1、c2为时效因子回归系数;Hu为上游水位,mm;Hd为下游水位,mm;Hu0、Hd0分别为始测日所对应的上、下游水位,mm;T为气温,℃;t为始测日至监测日的累计时间,d;θ为相对于始测日的累计时间除以100。
为验证M-ELM大坝变形安全监控模型在解决大坝变形监测数据的因子不确定性、非线性及抗粗差性等方面的优越性,以该水利工程大坝变形原型监测资料为基础,分别进行传统最小二乘法OLS(ordinary least squares)、人工神经网络ANN(artificial neural network)及稳健估计极限学习机M-ELM监控模型的建立和拟合预测对比分析。
3.2.1OLS、ANN监控模型和分析结果
采用传统最小二乘法和人工神经网络方法进行回归计算所得出的模型拟合及残差效果示例见图3和图4。从图3和图4可以看出,OLS、ANN监控模型在处理含有异常值的原始数据时,在异常值附近,拟合曲线虽然具有较好的拟合效果,但基本包含了全部异常值的影响,致使拟合曲线发生跳跃,出现追逐异常值的现象。同时,ANN监控模型在图中表现出了其固有的过拟合缺陷,因此两种模型的抗粗差能力弱的弊端致使建立的大坝变形监控模型难以进行实际应用,极大地降低模型预测能力甚至得出错误的结果。
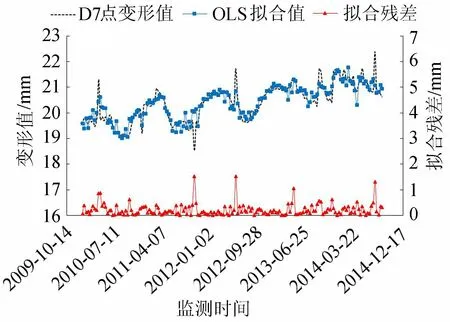
图3 OLS监控模型拟合及残差效果

图4 ANN监控模型拟合及残差效果
3.2.2M-ELM监控模型分析结果
采用M-ELM算法建立大坝变形监控模型时,根据训练结果的均方差进行网络隐含层节点数的选取,以确保网络训练结果的误差最小,并得到最优的网络参数。模型训练过程中拟合值与实测值均方差与隐含层节点数的关系见图5,当隐含层节点数取15时,训练结果的均方差达到最小值0.370 9,因此在本次训练中选取隐含层节点数为15。同样以D7监测点为例,M-ELM大坝变形监控模型分析结果见图6。从图6可以得出:①M-ELM模型很好的抵抗了异常点对模型计算参数的影响,在异常点处不会产生追逐现象,并且具有很好的拟合效果;②拟合残差在异常值处表现出了明显的波动现象,具有良好的异常值识别能力。综合以上两点可以得出,采用M-ELM算法建立的安全监控模型不仅具有较高的拟合精度,同时也具有极强的粗差抵抗能力。

图5 模型训练误差与隐含层节点数的关系

图6 M-ELM监控模型拟合及残差效果
3.2.3模型性能对比分析
选取该大坝相同测点2014年6月1号至2014年12月11号之间共20个样本作为两种模型的测试样本,以反映模型预测精度的均方误差MSE和平均绝对百分误差MAPE及反映模型鲁棒性的中位数绝对偏差MAD进行模型预测效果评价:
(12)
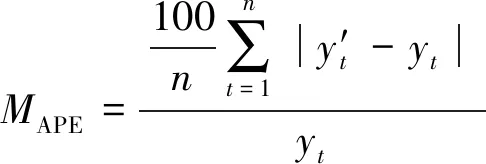
(13)

(14)
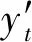
3种大坝变形监控模型预测结果对比如表1和图7所示(图表中将2014年7月11日异常值22.378 mm修正为21.072 mm,预测值指标计算采用修正值)。

表1 OLS、ANN、M-ELM监控模型预测效果对比
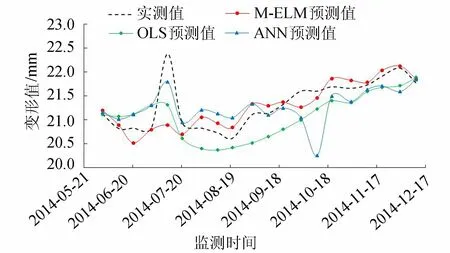
图7 3种模型预测值与实测值对比
从表1及图7可知,M-ELM监控模型预测的均方误差为0.145 57、中位数绝对偏差为0.161 42、平均绝对百分误差为1.368 33,模型精度明显优于OLS和ANN监控模型;在异常监测值处M-ELM监控模型预测结果表现出了明显的鲁棒性和泛化性,对于监测数据中的粗差具有很强的抗干扰能力,预测值具有良好的实际参考价值,而OLS和ANN监控模型却表现出了明显的波动现象。
4 结 论
a. 针对水利工程监测数据存在的非线性、多重共线性及传统最小二乘法抗粗差能力差等问题,将稳健估计理论引入极限学习机模型中,建立的基于稳健估计极限学习机的大坝变形监控模型避免了过学习现象,具有较高的拟合和预测精度,并且同时兼有强鲁棒性和泛化性,其在监测数据拟合预报分析方面具有良好的实用价值。
b. 基于稳健估计极限学习机的大坝变形安全监控模型仍旧属于静态预报模型,而且属于智能算法中的浅层结构,在挖掘信息的内部特征来反映结构的真实性态方面还存在一定的缺陷。
c. 随着特大型水利工程建设的发展,将在线动态学习与之结合,建立大坝安全实时监测系统,实现监测自动化是水利工程安全监控的发展趋势,这些对于监测数据处理的时效性和准确性提出了更高的要求,因此仍需进一步深度挖掘水利工程安全监测数据中的内部特征,了解其真实的运行性态。

