基于节点位置相关性分析的结构位形推算方法

刘俊 罗永峰 杨旭 栗云松

摘    要：既有空间结构鉴定计算应按结构实际位形建立几何模型.根据空间结构几何构造特性，采用节点位置偏差相关系数的函数模型分析节点位置相关性并给出模型参数确定方法;基于节点位置相关性分析，提出根据抽样测量节点位置推算结构几何位形的方法，以条件概率分布期望作为未测节点实际位置偏差的期望估计值，以交叉验证的方差置信上限作为偏差的方差估计值，由此确定偏差分布，得到结构实际几何位形，建立结构鉴定计算的不确定模型.对实际网壳结构根据抽样测量节点位置推算结构实际几何位形，并进行整体稳定性分析.研究结果表明，基于节点位置相关性分析的推算方法结果更符合实际.

关键词：空间结构;鉴定分析;位形推算;节点位置相关性

中图分类号：TU393.3                           文献标志码：A

Abstract：In both the analysis and appraisal of existing spatial structures，structures should be modeled in accordance with the actual geometric shapes. A function of correlation coefficient was recommended to model the correlated deviation of nodal positions according to the geometric characteristics of the existing spatial structures， and the approach to calculating model parameters was given. Based on the correlation analysis of nodal positional deviations，a new method of reckoning the structural geometric shapes by sampling nodal positions was proposed. In the proposed method， the deviation distributions of unmeasured nodal positions can be inferred from sampling data where expectations should be calculated by conditional distributions and variances would be estimated as upper limits of the confidence intervals from the cross validation. Then， using the calculated deviation distributions， uncertain geometric models can be established to analyze and assess the existing spatial structures. Through calculating the shell shape by sampling the nodes and analyzing its overall stability， it concludes that the method based on nodal positions correlation analysis meets the actual case. The proposed method was applied to reckoning the geometric shape of a reticulated shell structure，and the nonlinear static stability analysis was carried out. It is shown that the proposed method can give reliable results and apply to the appraisal of existing spatial structures.

Key words：spatial structure;structural analysis and appraisal;geometric reckoning;nodal positional correlation

對既有空间结构进行定期或适时的检测、鉴定与维护，是保障结构安全且正常使用的前提和必要条件[1-2].国内外规范[3-4]均指出，既有结构鉴定分析采用的计算模型应是根据结构实际状况建立的二维或三维模型.然而，对既有空间结构的几何位形进行完全测量是不经济且没有必要的，有时甚至是不可能的，因而，实际工程结构检测通常采用抽样测量的方法.但是，抽样测量只能获得部分节点位置信息，要建立符合实际状况既有结构几何模型，必须根据已测量节点位置及结构设计信息，推算未测量节点位置，形成结构实际整体几何位形.

目前，由于缺乏关于既有结构整体位形反演推算的理论成果，实际结构工程鉴定中未测节点位置往往采用设计位置.对于单层网壳结构等缺陷敏感型空间结构，几何缺陷是影响结构整体稳定承载力的关键因素之一[5-7].因此，当未测节点位置采用设计位置时，则必须考虑结构几何缺陷，而实际工程鉴定分析中，结构几何缺陷仍按设计方法考虑.设计假定的缺陷与结构实际缺陷可能完全不同，这将导致鉴定分析结果与结构实际状态可能存在很大差异.对于此，罗立胜等[8]研究认为，采用不确定模型进行结构鉴定计算更为合适;罗永峰等[9]提出推算结构实际几何位形的随机偏差方法，根据已测节点位置推断未测节点位置偏差分布，建立不确定几何模型.此类方法基于节点空间位置的不确定性和随机分布特性.由于空间结构节点位置偏差受安装设备、安装技术、工人技术水平等多种因素影响，因而偏差一般具有明显的随机分布特征，同时，实际工程测量数据表明[10-12]，节点位置偏差往往服从正态分布.但是，不同节点的偏差分布可能并非相互独立，Chen等[10]在对单层网壳结构初始整体几何缺陷的研究中指出，结构邻近节点的实际位置偏差具有相关关系，并采用实际单层网壳结构节点位置偏差实测数据进行了验证.现有推算既有空间结构节点位置的随机偏差方法假定不同节点位置偏差相互独立，未考虑节点实际位置偏差可能存在的相关性.推算结构实际几何位形时，忽略实际存在的节点位置偏差相关关系，会导致抽样测量数据提供的相关性信息被忽略，未测节点位置推算结果的准确程度降低，结构鉴定分析结果与实际状况差异增大.

基于此，本文针对既有空间结构几何位形的推算方法进行研究，提出基于节点位置相关性分析的位形推算方法.该方法首先根据节点位置抽样测量数据，拟合节点实际位置偏差的相关系数函数模型;然后，基于节点位置相关性分析结果，通过抽样测量数据推算未测节点实际位置偏差分布;最后，根据偏差分布推算结果建立既有空间结构鉴定计算的几何模型.

1   节点位置相关性

1.1   偏差的相关性

节点位置相关性是指结构不同节点实际位置偏差的相关性.既有空间结构邻近节点的位置偏差往往具有一定相关性，节点位置抽样测量数据可以为未测节点位置推算提供有效信息.

例如，假定结构中2个节点同一方向位置偏差X1和X2均服从正态分布，即X1～N（μ1，σ21）、X2～N（μ2，σ22），其中μ1和μ2为分布的期望，σ21和σ22为分布的方差，则其密度函数分别为：

记X1和X2的相关系数为r，此时，X1和X2服从联合正态分布，其联合密度函数为：

根据概率论与数理统计理论，某一随机事件在另外一个事件已经发生条件下的发生概率被称为条件概率.若已知X1的测量值x1，则X2的条件概率密度函数可由

相较于X2的原正态分布，可以发现X2的方差由σ22降低为σ22（1-r2），由此可见，X1的实测值x1可以为X2分布推断提供一定信息，使X2方差减小.考虑极端情况，若X1和X2同分布，且相关系数 r=1，此时X2方差降低为0.这表明得到X1实际值为x1，则可以以100%概率推断X2 = X1.由此可见，若节点之间存在相关性，基于条件概率理论，必须考虑节点位置相关性才能充分利用抽样测量数据信息，提高偏差分布推断准确程度.

1.2   协方差与相关系数

考虑既有空间结构节点位置相关性，应首先对不同节点位置偏差的相关关系进行定量分析.概率论和数理统计理论中，主要采用协方差和相关系数描述变量之间的相关性大小.以随机变量表示节点实际位置与设计位置偏差，空间结构节点同一方向位置偏差变量集合可以表示为（X1，X2，…，XN），其中N为节点总数量，同时，变量对应的实际偏差值记为（x1，x2，…，xN）.分别以E、var和cov表示变量的期望、方差和协方差，则对于任意第i和第j个节点，偏差Xi和Xj的协方差定义为：

相关系数反映了随机变量间的线性相关程度[13]， r越大，相关程度越大; r最大为1，此时两个变量完全线性相关;而 r = 0则表明两个变量之间不相关.此外，r的正负分别表示正相关和负相关.

协方差与相关系数均为定量描述相关性大小的参数，特别是，若（X1，X2，…，XN）同分布，则方差为常量，记为σ2，由式（8）可得：

表明协方差是相关系数与常量的乘积，此时，协方差与相关系数呈完全正比关系.由于相关系数是无量纲参数，易于对比分析，因此，本文选用相关系数作为定量描述节点位置相关性的参数.

1.3   相关系数函数模型

既有空间结构节点数量往往较多，为求不同节点之间相关系数，首先需要根据既有空间结构几何构造特性和节点位置偏差分布特征，确定一个合理且实用的相关系数数学函数模型.节点位置相关性受结构网格划分形式、结构安装方式和施工技术水平等多个因素影响，难以根据全部影响因素建立函数模型.Chen等[10]指出节点距离越近，相关性越强，并提出以两节点之间最小杆件连接数为相关系数函数的自变量.本文根据既有空间结构几何构造特点和空间整体性，假定节点位置相关性仅取决于节点间距离，节点之间距离越大相关性越小.因此，相关系数是节点距离的函数，即

其中，d为第i个节点与第j个节点设计位置之间的距离.r（d）应满足d=0时r最大为1;随着d增大，r逐渐较小;当d较大时，r接近或等于0.基于此变化特点，理论模型可采用线性模型、球状模型和高斯模型等[14]，以高斯模型为例，

其中，θ为待定参数.高斯函数图像如图1所示.由图1可知，此模型符合相关系数变缓特点.相关系数函数模型的参数，可根据节点位置抽样测量数据计算得到.同时，对函数模型拟合实际工程测量数据的准确程度进行分析，若函数模型能较好拟合样本数据，则假定模型的合理性得到验证.

2   节点位置推算

2.1   偏差分布推断

施工误差引起既有空间结构几何位形偏离设计位形时，节点实际位置应是以设计位置为中心的随机分布，因此，节点位置偏差应服从期望为零的某种概率分布，一般认为偏差近似服从正态分布.

假定既有空间结构节点位置偏差服从期望为零、方差为σ2的正态分布， T为n个抽样测量节点位置偏差，相关系数矩阵R定义为：

则X的概率密度函数为：

记X0为某一未测节点位置偏差，那么相关系数向量 r可以定义为：

抽样测量得到X的样本值x=（x1，x2，…，xn）T之后，X0的概率分布变为条件概率分布，由条件概率密度计算公式[15]可计算得到X=x时X0的条件概率密度函数为：

根据正态分布密度函数可知，X0条件概率服从正态分布，即X0～N（rTR-1x，（1-rTR-1r）σ2）.基于此条件概率分布，可以认为X0的期望估计值方差估计值可以证明[16]，期望的估计值 0是最优线性无偏估计（简单Kriging估计），对于非正态分布依然成立.一般rTR-1r < 1，因此 20 < σ2，表明推断分布的方差小于原分布方差.因而，本文方法偏差分布推斷结果精度，高于忽略节点相关性的推断结果.

2.2   相关系数模型及参数确定

估计式（19）（20）中含有2个未知参数，即方差σ2以及用于计算R和r的相关系数模型参数 .采用估计公式进行偏差分布推断时，首先需要确定相关系数函数模型，并根据抽样测量数据估计参数 σ2和θ.由此可构建函数

则R（d）中恰好包含未知参数σ2和θ.随机过程理论中， R（d）被称为自相关函数，简称相关函数，根据抽样测量数据拟合得到相关函数，就可以得到参数σ2和θ.

首先，根据n个抽样节点位置偏差（x1，x2，…，xn），对于任意第i和第j个节点，分别计算两节点距离dij及偏差乘积xi xj，可以得到R（d）的多组观测值 （dij，xi xj）（i，j∈N;i≠j）.然后，绘出（dij，xi xj）的散点分布图，由于σ2为定值，自相关函数R（d）趋势与相关系数函数模型r（d）相同，因此，根据散点图趋势可以选定合适的相关系数模型.

实际工程中数据（dij，xi xj）分布散乱，往往需要通过对距离dij进行分组并计算均值作为R（d）的观测值.首先给定组宽2d0，确定距离dij落在区间[dm - d0，dm + d0]内的所有数据对，然后计算偏差乘积的均值，记为Rm，得到新的M组数据对（dm，Rm），由此绘出R（d）的散点图.

根据散点数据拟合相关函数方法有多种[17]，最简单实用的方法是非线性最小二乘法.相关系数模型选定之后，乘以参数σ2得到R（d）的数学函数模型，以此作为非线性回归模型对M组数据进行回归分析.采用非线性最小二乘法对回归模型的参数进行估计，构造函数求解使得其达到最小的σ2和θ，就可得到参数的最小二乘估计.若相关系数选用高斯模型等连续可导函数，R对 σ2和θ也均连续可导时，此时，可以利用微分法建立非线性最小二乘估计的正规方程组：

求解该方程组即可得到参数σ2和θ的最小二乘估计.

若相关系数模型（球状模型或线性模型等）对 θ非连续可导时，需要通过最优化计算方法，直接求解使式（23）最小的σ2和θ，得到参数估计值.

2.3   方法适用性

本文方法假定相关系数是节点距离的函数，若相关函数散点图显示节点相关性与节点距离没有趋势的明显变化关系，则本文方法不适用，偏差分布推断应采用独立样本的传统统计推断方法.

由式（20）可以得出方差估计值，但是由于相关系数模型与实际存在差异等原因，方差估计值可能与实际值存在一定差异.对已测节点数据进行交叉验证，由于交叉验证结果包含模型差异因素，因此，采用交叉验证方差作为未测节点位置偏差的方差更为准确合适.按照本文方法的计算式（19）计算偏差的期望估计值，以交叉验证结果的方差作为方差估计值，就可以得到未测节点位置偏差分布.将未测节点以设计位置为中心，按推断的偏差分布建立不确定模型，可进一步进行蒙特卡罗有限元计算和结构鉴定分析.

3   案例分析

3.1   结构信息

既有单层钢网壳模型跨度为3.6 m，矢高为0.9 m，体系为5环K6型，共91个节点（30个支座节点），如图2所示.杆件截面均为？准6×1，焊接球半径为70 mm，材料均为Q235钢，节点为刚接节点，支座为刚接支座.

3.2   节点位置相关性

测量全部节点坐标，分别计算X、Y、Z方向上的节点实际位置与设计位置偏差.根据实测偏差数据，分别计算不同节点同一方向上偏差乘积.对节点距离进行分组，组宽取200 mm，计算落入同一组内乘积的均值，得到相关函数的37个观测值，绘出散点分布图（如图3所示）.

由图3可知，X、Y方向上节点相关性与距离存在明显的下降趋势变化关系，随着节点距离达到一定值，下降趋势转变为水平趋势，且相关函数值在0附近波动;Z方向散点图无明显趋势变化关系.因此，可以认为，X、Y方向上邻近节点之间具有偏差相关性，随着节点距离增加，相关性逐渐减小，而Z方向上节点位置偏差没有明显相关关系.

实际网壳的实测数据表明，既有空间结构X、Y方向不同节点位置偏差具有一定相关关系.同时，节点偏差的相关系数与节点距离存在明显趋势关系，相关系数与节点距离变化关系符合本文第2.2节

假定.

3.3   节点位置推算

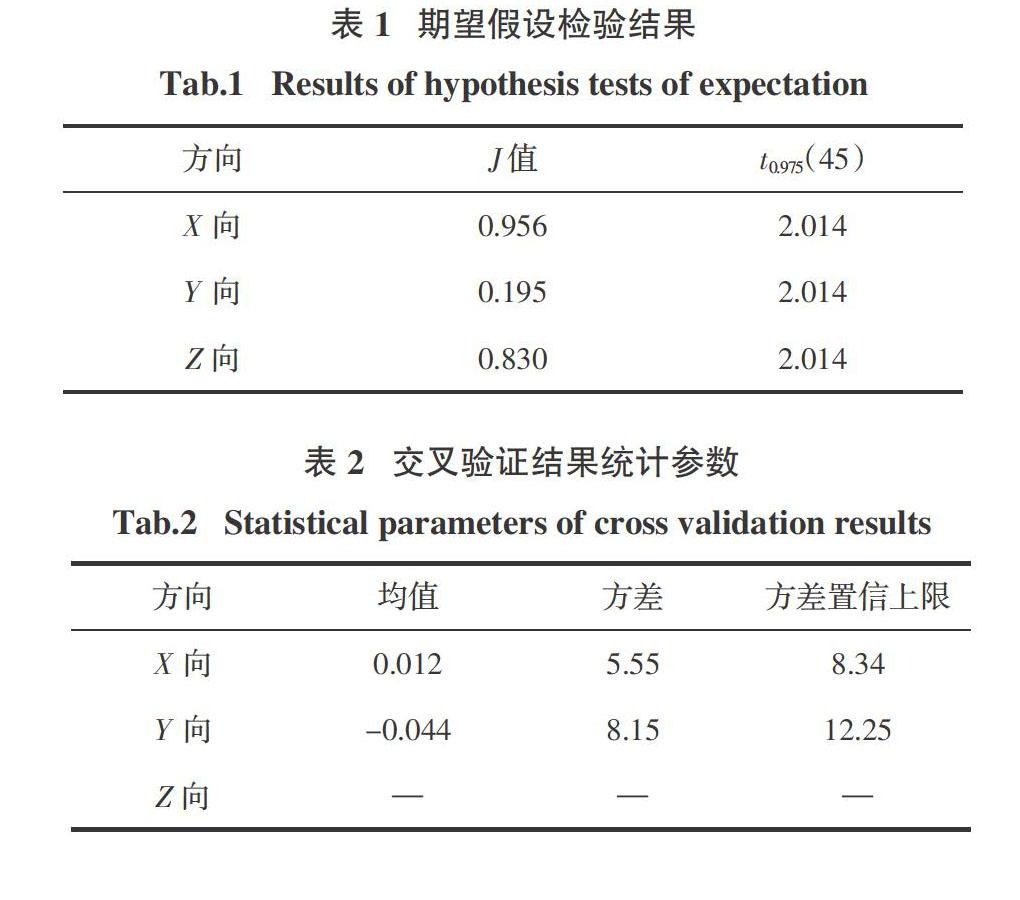
本算例忽略测量误差，选取1，3，···，91号共46个节点作为抽样测量节点，其余节点作为未测节点.计算实际节点位置坐标与设计节点位置坐标偏差，对节点偏差进行期望为零的假设检验，结果如表1所示.由表1可知，各方向偏差都满足期望为零的假设，结构未发生较大使用变形.

相关系数函数选用高斯模型，对采用本文方法抽样测量数据进行交叉验证，分别将已测46个节点中的每个节点作为未测节点，其余45个节点作为已测节点进行推算.对交叉验证计算得到的 0与实测结果差值进行统计分析，结果见表2.

表2中交叉验证差值结果的均值非常接近零，验证了本文方法得到的偏差分布期望估计值 0是无偏性的.

计算得到的X方向和Y方向方差估计值 20均值分别为0.96和1.71，对比表2中交叉验证方差可以发现， 20的均值明显小于交叉验证方差.理论上两者应较为接近，但由于相关模型与实际存在差异等原因，交叉验证方差大于 20的均值，因此，采用交叉验证的方差作为未测节点位置偏差方差的估计值更合适，偏于保守，可采用95%置信区间估计的上限值σ2L.

按照本文方法，基于节点位置相关性推算未测节点位置，抽样测量数据表明，X方向和Y方向上节点位置偏差具有明显相关关系，因此，对X方向和Y方向偏差进行推算.

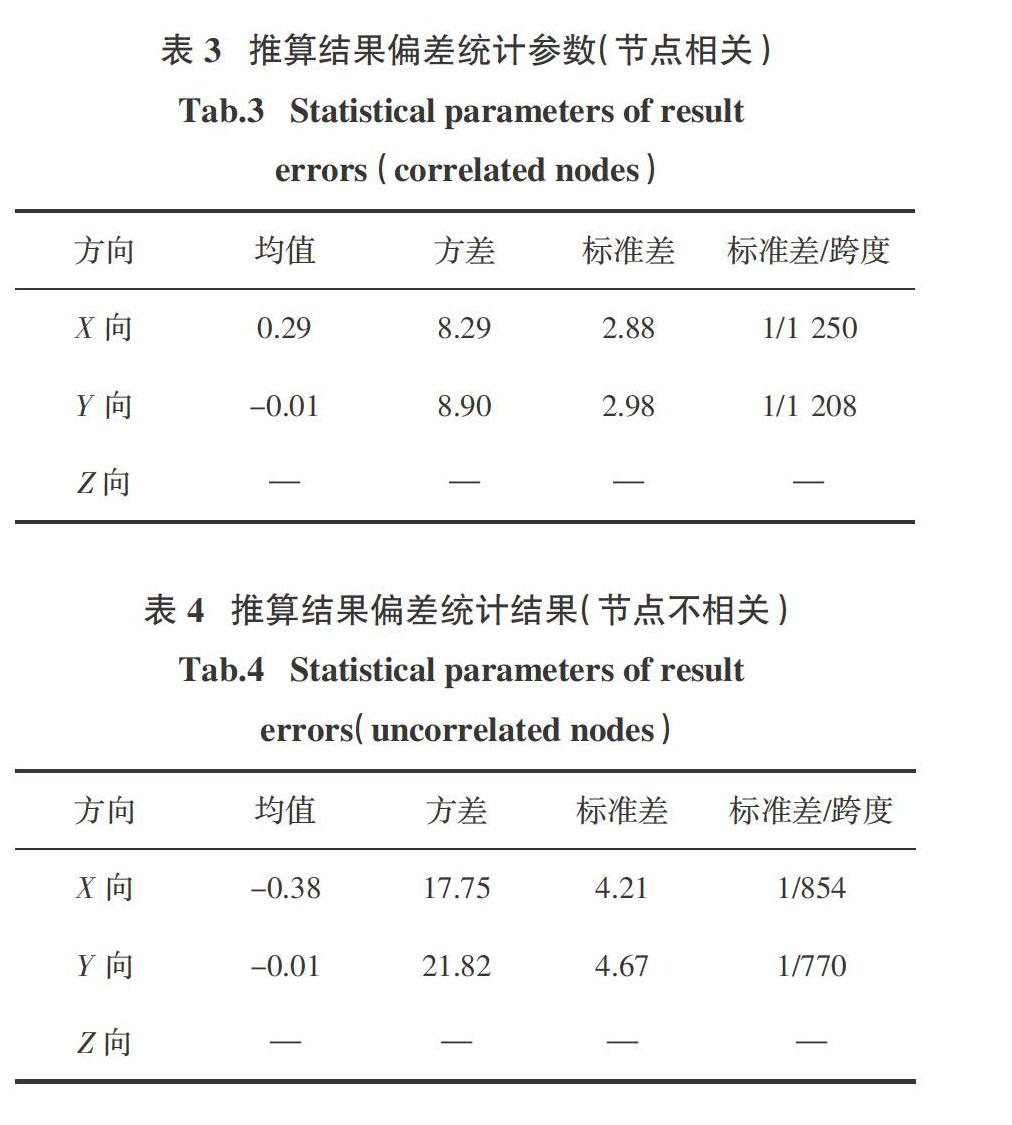
推算结果的 0与实测结果差值的统计分析结果如表3所示.推算差的均值接近零，表明以推斷得到的 0作为未测节点位置偏差推算值，结果较为准确;推算差的方差接近但小于σ2L，表明以结果的方差置信上限σ2L作为方差的估计是合理的且偏于保守的.

假定各節点位置偏差相互独立，计算得到偏差分布的期望估计和方差估计，统计分析X方向和Y方向期望估计值与未测节点实际值的差值，结果见表4.对比表3与表4结果，可以发现本文方法推测结果偏差的方差更小，精度更高.

3.4   结构鉴定分析

以结构实际整体稳定承载力为例进行鉴定分析，采用有限元软件ANSYS进行建模计算.杆件选用BEAM188单元模拟，材料选用理想弹塑性模型.节点为刚接节点，支座为固定支座，模型中考虑焊接球为节点刚域.荷载为满跨均布0.5 kN/m2恒载和均布0.75 kN/m2活载，荷载组合为1.0恒+1.0活.

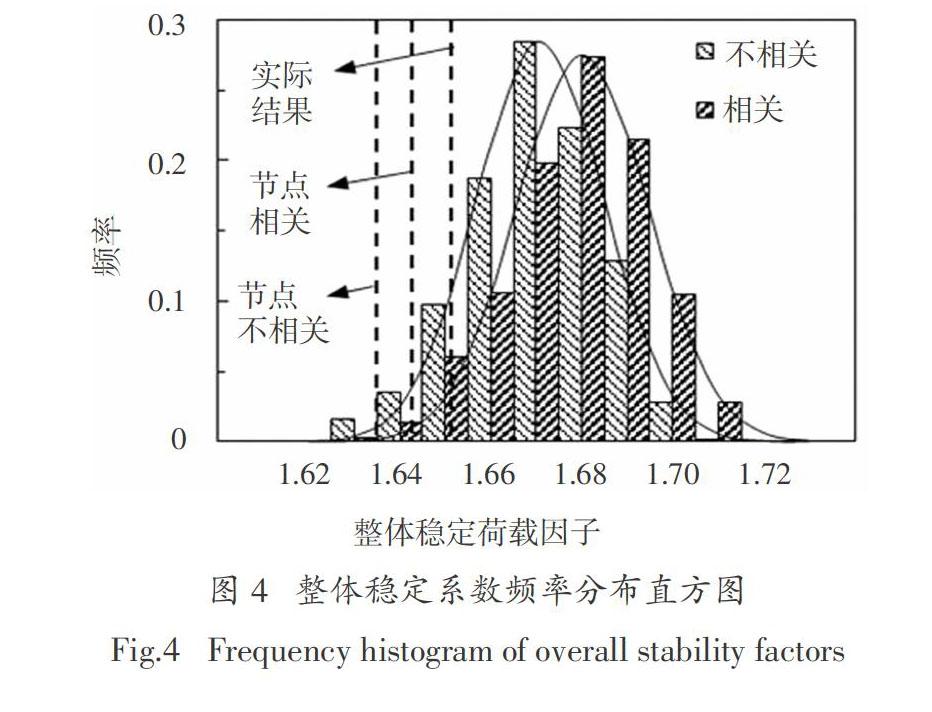
利用ANSYS软件PDS模块进行蒙特卡罗随机有限元分析，未测节点以设计节点为中心，X和Y方向偏差分布依据本文方法计算结果，即期望为估计值 ，方差为交叉验证置信上限 ;Z方向偏差由于无明显节点位置相关性，因此采用普通统计推断方法结果.1 000次随机输入的概率分析计算结果如图4所示，具有95%可靠度的整体稳定荷载因子为1.643.

整体稳定荷载因子按不考虑节点相关性的偏差分布推断结果，1 000次随机输入的概率分析计算结果如图4所示，具有95%可靠度的整体稳定荷载因子为1.635.对所有节点位置全部测量，建立完全符合实际的几何模型，计算得到整体稳定性荷载因子为1.651，对比可知，同样偏于安全的情况下，本文方法结果更加接近实际.

4   结   论

本文针对既有空间结构几何位形的推算方法进行研究，得到的研究成果及结论如下：

1）基于既有空间结构节点实际位置偏差的相关性，提出根据已测节点位置及节点位置相关性推算未测节点位置偏差分布，得到结构实际几何位形推算方法.根据本文方法可以建立既有空间结构鉴定计算的不确定几何模型，进行结构鉴定分析.

2）根据空间结构特点，采用以节点距离为自变量的节点位置偏差相关系数函数模型，进行既有空间结构节点位置相关性分析，并给出模型参数确定方法.

3）基于概率论和数理统计理论，根据已测节点实际位置偏差及节点位置相关性分析结果，提出以条件概率分布期望作为未测节点实际位置偏差分布的期望估计值;以交叉验证方差的置信上限作为偏差分布的方差估计值，得到偏差分布.

4）本文方法考虑了不同节点位置偏差的相关性，相较于现有方法，偏差分布推断更为准确.实际案例分析表明，基于本文方法的鉴定分析结果更符合结构实际状态，本文方法的可行性与合理性得到验证.

参考文献

[1]    罗永峰. 国家标准《高耸与复杂钢结构检测与鉴定技术标准》编制简介[J].钢结构，2014，29（4）：44—49.

LUO Y F. Brief introduction of composition of technical standard for inspection and appraisal of high-rising and complex steel structures[J]. Steel Construction， 2014， 29（4）： 44—49. （In Chinese）

[2]    罗立胜，罗永峰.既有网格结构构件重要性实用判定方法[J].结构工程师，2017，33（2）：109—114.

LUO L S，LUO Y F. A practical method for evaluation of member importances of existing spatial structures[J]. Structural Engineers，2017，33（2）：109—114.（In Chinese）

[3]    GB 51008—2016   高耸与复杂钢结构检测与鉴定标准[S]. 北京：中国计划出版社，2016：6—7.

GB 51008—2016  Technical standard for inspection and appraisal of high-rising and complex steel structures[S]. Beijing：China Planning Press，2016：6—7.（In Chinese）

[4]   ISO 13822—2010  Technical committee bases for design of structures-assessment of existing structures[S]. Switzerland：International Organization for Standardization，2010：9.

[5]  MALEK S，WIERZBICKI T，OCHSENDORF J. Buckling of spherical cap gridshells：A numerical and analytical study revisiting the concept of the equivalent continuum[J]. Engineering Structures，2014，75：288—298.

[6]   BRUNO L，SASSONE M，VENUTI F. Effects of the equivalent geometric nodal imperfections on the stability of single layer grid shells[J]. Engineering Structures，2016，112：184—199.

[7]   LIU H，ZHANG W，YUAN H. Structural stability analysis of single-layer reticulated shells with stochastic imperfections[J]. Engineering Structures，2016，124：473—479.

[8]    罗立胜，罗永峰，郭小农.考虑节点几何位置偏差的既有网壳结构稳定计算方法[J]. 湖南大学学报（自然科学版），2013，40（3）：26—30.

LUO L S，LUO Y F，GUO X N. Overall stability of existing reticulated shells considering the effect of geometric position deviation of joints[J]. Journal of Hunan University（Natural Sciences），2013，40（3）：26—30.（In Chinese）

[9]    罗永峰，刘俊. 既有空间结构位形推算的随机偏差方法[J]. 同济大学学报（自然科学版），2017，45（6）：791—798.

LUO Y F，LIU J. Stochastic deviation method of reckoning geometric shapes of existing spatial structures[J]. Journal of Tongji University（Natural Science），2017，45（6）：791—798. （In Chinese）

[10]  CHEN G，ZHANG H，RASMUSSEN K J R，et al. Modeling geometric imperfections for reticulated shell structures using random field theory[J]. Engineering Structures，2016，126：481—489.

[11]  刘学春，张爱林，葛家琪，等. 施工偏差随机分布对弦支穹顶结构整体稳定性影响的研究[J]. 建筑结构学报，2007，28（6）：76—82.

LIU X C，ZHANG A L，GE J Q，et a1. Study on the influence of construction deviation random distribution on the integral stability of suspend-dome[J]. Journal of Building Structures，2007，28（6）：76—82.（In Chinese）

[12]  唐敢，黎德琳，赵才其，等.空间结构初始几何缺陷分布规律的实测数据及统计参数[J].建筑结构，2008，38（2）：74—78.

TANG G，LI D L，ZHAO C Q，et a1. Statistical regulation and parameter study on initial geometrical imperfections of spatial structures based on measured data[J]. Building Structure，2008，38（2）：74—78. （In Chinese）

[13]  TAYLOR R.Interpretation of the correlation coefficient：a basic review[J]. Journal of Diagnostic Medical Sonography，1990，6（1）：35—39.

[14]  ONYEJEKWE S，KANG X，GE L. Evaluation of the scale of fluctuation of geotechnical parameters by autocorrelation function and semivariogram function[J]. Engineering Geology，2016，214：43—49.

[15]  茆詩松，王静龙，濮晓龙.高等数理统计 [M].第2版.北京：高等教育出版社，2006：344—346.

MAO S S，WANG J L，PU X L. Advanced mathematical statistics[M]. 2nd ed.Beijing：Higher Education Press，2006：344—346. （In Chinese）

[16]  CRESSIE N. The origins of kriging[J]. Mathematical Geology，1990，22（3）：239—252.

[17]  SOLTANIMOHAMMADI S，SAFA M. A simulated annealing based optimization algorithm for automatic variogram model fitting[J]. Archives of Mining Sciences，2016，61（3）：635—649.