冲击荷载下钢筋混凝土梁局部响应特征研究

赵武超 钱江

摘   要：从分析已有冲击试验结果入手，将钢筋混凝土梁的动态响应区分为局部响应阶段和整体响应阶段.由于钢筋混凝土梁在局部响应阶段更易发生脆性剪切破坏，本文主要研究此阶段梁的瞬态响应.讨论了惯性力和负向支座反力对梁内力分布的影响;根据荷载平衡基本原理和参数分析结果建立了梁内力分布的计算方法.结果表明：惯性力和负向支座反力均会影响梁体局部响应阶段的内力分布;负向支座反力近似与梁的跨高比和碰撞力呈线性关系;将惯性力的分布简化为线性分布能够较好地反映梁的实际受力状态.

关键词：钢筋混凝土梁;冲击荷载;瞬态响应;惯性效应;支座反力;内力分析

中图分类号：TU375                          文献标志码：A

Abstract： Based on the existing experimental results， the dynamic response of RC beams under impact loading is divided into local response stage and overall response stage. As RC beams are vulnerable to shear failure during the local response stage， this study investigates the transient response of the components in this stage. Thus， the effect of inertial force and reverse reaction on the internal force distribution at the local response stage is also discussed. Based on the basic principles of force equilibrium and parametric analysis results， a computing method for the internal force of RC beams is proposed. The results show that both the inertial force and negative reverse reaction affect the internal force distribution of beams during the local response stage， and the reverse reaction is approximately linear to the span-depth ratio and peak impact force. The assumption that the distribution of inertial force is linear can well reflect the actual force state of the beam.

Key words：RC beams;impact loading;transient response;inertia force;reverse reaction;internal force analysis

船、車撞击桥梁[1-2]、飞行物撞击建筑物和核电厂房、山区落石撞击相邻建筑物和构筑物等事故都有可能造成结构的严重损伤甚至倒塌，因此，在工程结构设计中外部冲击荷载应给予极大的关注.钢筋混凝土构件作为结构中常见的受力构件，其在冲击荷载下的瞬态响应和抗撞性能对结构设计具有重要意义.

近年来国内外学者对冲击荷载下钢筋混凝土构件的动态响应进行了一系列试验研究和数值仿真研究.Hughes等[3]进行了92根钢筋混凝土梁的冲击试验，研究了冲击速度、冲击质量和接触刚度对构件动态响应的影响，并指出等效静力设计方法由于不能反映高阶振型的贡献，因此不适用于构件的抗撞设计.Kishi等[4]采用落锤冲击试验研究了无腹筋钢筋混凝土梁在冲击荷载下的动态响应和耗能能力，并指出支座反力比碰撞力更能反映构件内力和抗冲击能力.随着冲击速度的增大，钢筋混凝土构件的破坏模式由弯曲破坏转变为剪切破坏.Saatci等[5]通过落锤试验研究了钢筋混凝土梁的抗剪机制对其抗撞性能的影响，结果表明抗剪机制对构件的弯曲破坏和剪切破坏均发挥了重要作用.Fujikake等[6]研究了钢筋混凝土梁在冲击荷载下的动态响应，并建立了预测最大冲击力和最大变形的弹簧-质量模型.许斌等[7]开展了钢筋混凝土梁抗冲击性能的试验研究，分析了冲击过程中梁的裂缝发展和破坏形态.王明洋等[8]基于弯曲理论建立了钢筋混凝土梁在弹塑性阶段时碰撞力和变形的计算公式.刘飞等[9]从损伤发展和冲击能量转化方面分析了钢筋混凝土构件的冲击响应过程和破坏机理.Kishi等[10]基于36根钢筋混凝土梁冲击试验建立了以最大变形和残余变形为指标的抗冲击设计方法.赵德博等[11]结合冲击试验结果对Kishi等[10]提出的设计方法进行了改进.

理论分析方面，Jones[12]采用移行铰概念建立了钢结构构件冲击响应的分析模型，其中假定梁体材料为理想刚塑性，梁的加速度和速度呈三角形分布.在碰撞开始时刻，梁在撞击处迅速形成塑性铰.随着应力波的传播，应力波到达位置也形成了塑性铰，并逐渐向构件端部移动.移行铰的概念比较清晰，便于理论推导，因此在刚塑性结构力学中得到广泛应用.Symonds等[13]指出移行铰的概念只是假想的，并不具有实际物理意义.刚塑性模型仅考虑应力波沿梁轴向方向传播情况，忽略了其厚度效应.邢誉峰等[14]采用间接模态叠加方法对质点和简支平面应力梁的撞击问题进行了分析，指出剪切变形和厚度效应对梁的冲击响应有重要影响.然而，钢筋混凝土材料本构与刚塑性模型相差较大，梁体很难形成“移行铰”，因此采用刚塑性模型来研究钢筋混凝土梁的动态响应可能会造成较大的误差.另一些学者从波动理论来考察钢筋混凝土梁在冲击荷载下的瞬态响应.童桦等[15]对混凝土中应力波的传播进行了研究.Cotsovos[16]建议采用“有效响应长度”概念来研究钢筋混凝土梁的动态响应.梁的有效长度定义为最大负弯矩之间的距离，碰撞力的传播速度定义为混凝土材料的剪切波速Vs.需要指出的是，Cotsovos采用的冲击荷载为斜坡力，而忽略了碰撞物体之间的相互作用.

冲击荷载下钢筋混凝土梁的动态响应可以分为局部响应阶段和整体响应两个阶段[6，17].梁体动态响应的既有研究大部分集中在整体响应阶段的碰撞力、构件的变形和破坏模式等方面，然而，这些对理解冲击荷载下结构构件的动态响应和破坏机理还不够全面和深入.由于局部响应阶段的持续时间比较短暂，试验测得的数据精度难以得到保证，因此局部响应阶段的研究相对较少.冲剪效应在局部响应阶段比较显著，此时梁往往在出现明显的变形之前发生脆性剪切破坏.只有在局部响应阶段梁不发生剪切破坏的前提下，才能保证整体响应阶段的弯曲破坏，同时局部响应阶段的损伤程度也会对整体响应阶段的承载能力产生影响.

由此可见，局部响应阶段梁的动态响应对碰撞过程具有不可忽视的贡献.本文首先采用有限元软件LS-DYNA对文献[6]中的钢筋混凝土梁冲击试验进行了数值仿真，并验证了有限元模型的可靠性;结合惯性效应和支座反力分析了局部响应阶段梁的内力分布;最后通过大量的参数分析得到碰撞力峰值和支座反力的回归公式，从而建立了钢筋混凝土梁內力计算的经验公式.

1   模型建立与验证

本文基于Fujikake等[6]进行的落锤冲击试验对钢筋混凝土梁的动态响应进行数值模拟.试验梁总长1.7 m，截面尺寸为150 mm（宽）×250 mm（高）;两端简支，净跨为1.4 m.梁截面采用对称配筋，顶面和底面分别配置两根直径为16 mm的纵向钢筋，其屈服强度为426 MPa;箍筋采用屈服强度为295 MPa、直径为10 mm的钢筋;箍筋间距为75 mm.梁几何尺寸和配筋信息如图1所示.混凝土抗压强度为42 MPa，最大骨料粒径为10 mm.落锤质量为400 kg，冲头为曲率半径为90 mm的半球形刚体.落锤分别在距梁顶面0.15、0.30、0.60和1.20 m高度处自由释放来冲击梁体.

钢筋混凝土材料模型采用美国联邦公路局为进行钢筋混凝土护栏安全性分析而开发的连续帽盖模型（MAT_CSCM_ CONCRETE）[18].该模型能够较好地反映低围压下混凝土的应变率强化、刚度退化和应变软化等力学行为.混凝土的单轴抗压强度和最大骨料粒径分别取为42 MPa和10 mm，其它材料参数均可由软件自动生成.钢筋采用弹塑性随动硬化模型（MAT_PLASTIC_KINEM- ATIC），弹性模量为200 GPa，泊松比为0.3，塑性模量为1.5 GPa，失效应变为0.12.采用Cower-Symonds模型[12]来考虑材料应变率效应，钢筋动屈服强度为：

混凝土、落锤和支座装置均采用单点积分实体单元模拟，钢筋采用Hughes-Liu梁单元模拟，梁端锚板采用单点积分壳单元模拟.不考虑钢筋与混凝土之间的相对滑移，采用共节点方式实现两者之间的连接.为了缩减计算时间以及避免出现初始穿透，将落锤与钢筋混凝土梁的初始间距设置为1 mm.通过关键字*INITIAL_VELOCITY_GENERATION赋予落锤不同的初始速度来实现不同冲击高度的撞击作用.采用基于罚函数算法的*CONTACT_EROD- ING_SURFACE_TO_SURFACE来定义落锤与梁、支座装置与梁之间的接触关系.

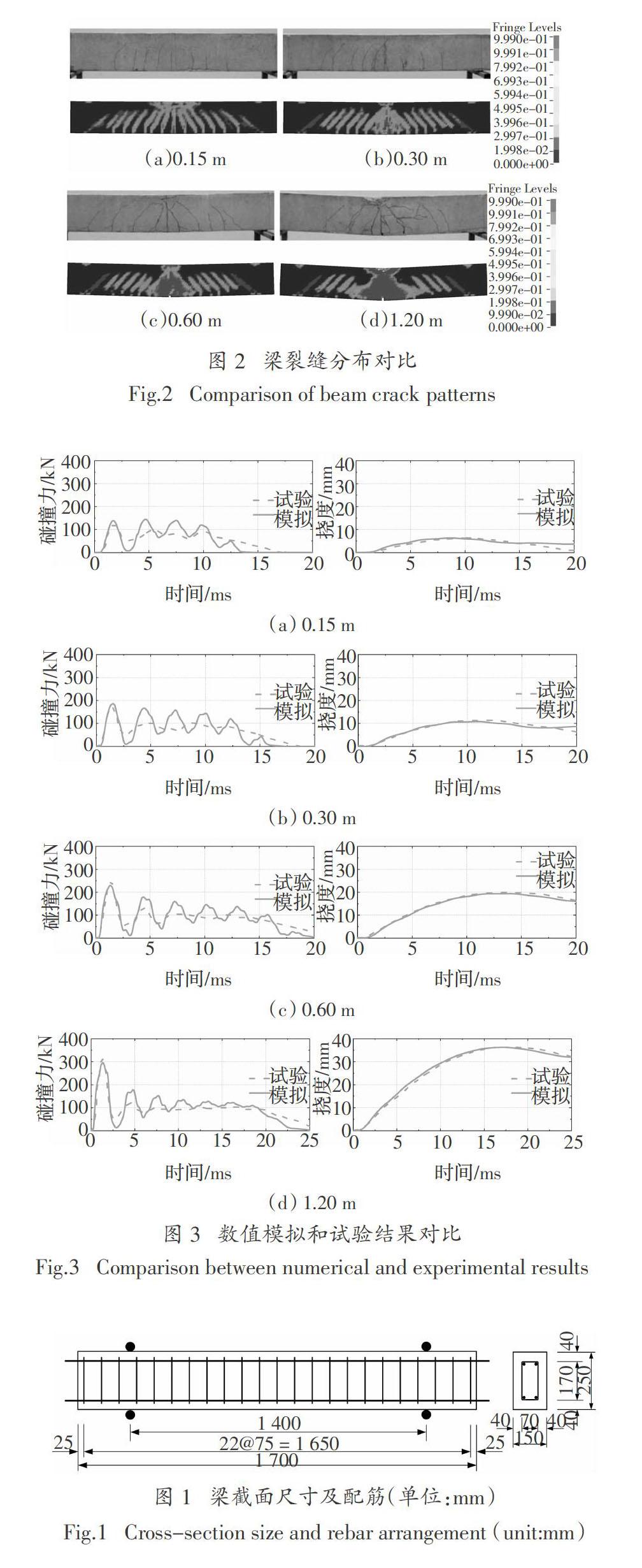
分别对比了在0.15 m、0.30 m、0.60 m和1.20 m冲击高度下钢筋混凝土梁动态响应的数值模拟和试验结果，其中裂缝分布、碰撞力和跨中挠度时程曲线如图2和图3所示.采用数值模拟得到的等效塑性应变分布来反映钢筋混凝土梁侧面裂缝分布.不同碰撞工况下数值仿真和试验得到的钢筋混凝土梁侧面裂缝分布和破坏情况基本一致.数值模拟得到的碰撞力时程曲线与试验结果比较接近，只是碰撞后期发生了一定的震荡，但首次碰撞阶段碰撞力吻合良好.与碰撞力相比，梁跨中挠度时程曲线与试验结果基本一致.可以看出，本文采用的有限元模拟方法和参数取值比较合理，可用于后续的仿真

2   仿真结果

为了深入探讨RC梁的内力分布，本文首先基于文献[6]中的冲击试验对钢筋混凝土梁在不同冲击速度下的碰撞力和支座反力进行分析.由于冲击试验为了研究梁的弯曲破坏性能而将抗剪能力设计过于保守，这里将箍筋间距调整为150 mm.同时，梁的净跨分别取为0.8、1.4和2.0 m;碰撞速度分别取3.4 m/s和13.7 m/s.不同碰撞工况下碰撞力和支座反力时程曲线如图4所示.当构件净跨为0.8 m时，碰撞力以极短的时间传递到支座处，此时大部分碰撞力由支座承担，冲击荷载对梁的瞬态响应和破坏模式影响不太明显.随着梁净跨的增加，惯性效应逐渐增强.在碰撞开始阶段支座反力出现了较大的负值，并且负向支座反力几乎与碰撞力同时达到最大值.负向支座反力随着碰撞速度和跨度的增大而增大;而梁的净跨对碰撞力峰值的影响并不明显.

许斌等[7]发现未施加预应力压梁的钢筋混凝土梁在初始碰撞阶段将会出现梁端部与支座脱离现象.Pham等[19]通过冲击实验得到的碰撞力和支座反力时程曲线如图5所示.在第一个碰撞力峰值区间，除了产生极大的碰撞力，还存在较大的支座负反力.与易造成碰撞点剪切破坏的碰撞力峰值相比，支座负反力更易被忽略.然而，支座反力会影响梁的内力分布，如最大负弯矩等.曾翔等[20]进行的冲击试验结果表明，裂缝的迅速发展甚至破坏就在几个毫秒内发生.这恰好表明，第一个碰撞力峰值区间内碰撞力峰值和支座负反力会显著影响梁的破坏形态.因此，本文对支座反力的研究中仅考虑碰撞力峰值区间的负反力.

3   讨   论

3.1   内力分析

负向支座反力主要是由于梁惯性力引起的，为了便于分析，这里定义γ为支座反力合力与惯性力的比值.剪切波在极短的时间内传播到支座处，此时碰撞作用对梁的影响较小，因此在理论分析时可以忽略该过程.在冲击荷载下梁惯性力沿长度方向的分布一般呈三角形和正弦分布.易伟建等[21]指出在碰撞力达到峰值之前惯性力沿长度的分布可以近似假定为线性分布.这里将惯性力沿梁长度方向假定为线性分布.基于Saatci等[5]和Pham等[22]的研究结果，这里简要地讨论了碰撞力峰值时刻梁的内力分布.当应力波传递到支座后，梁在冲击荷载下的内力分布如图6所示，其中l为梁净跨长度;a为悬臂长度;P为碰撞力;R为支座反力合力.

由于惯性力和負向支座反力的存在，钢筋混凝土梁的内力分布与静载下具有显著的差异.惯性力和负向支座反力不但改变了梁的弯矩分布，而且显著地减小了截面最大弯矩;尽管截面剪力的分布有所改变，但其最大值并未减小.局部响应阶段钢筋混凝土梁的抗弯需求降低，抗剪需求不变，从而造成其更易发生剪切破坏.此外，梁跨中出现了较大的负弯矩，同时反弯点的存在大大减小了碰撞部位梁的有效剪跨比，这些都会影响梁的受力机制.

3.2   支座反力对内力分布的影响

图7给出了不同净跨长度的梁跨中截面最大弯矩、截面最大负弯矩以及反弯点位置随负向支座反力的变化曲线.图中取λ = a/l;Mmax0为支座反力为零时梁跨中截面最大弯矩;Mneg0为支座反力为零时梁剪跨内最大负弯矩.负向支座反力对梁跨内最大负弯矩的影响作用随λ的增大而增大.当γ为0.1时，λ = 0.107的梁最大截面负弯矩约是不考虑负向支座反力时的3倍;而对于λ = 0.075的构件最大截面负弯矩甚至达到了不考虑负向支座反力时的7倍.梁跨中截面最大弯矩与γ呈线性关系，且随着支座反力的增大而减小.当λ较小时，截面最大弯矩对λ的变化不太敏感，当λ超过一定数值后，截面最大弯矩随着λ的增大而迅速减小.反弯点的存在改变了梁在冲击荷载下的受力模式，并有效地减小了梁的实际剪跨比，因此反弯点的位置对梁的动力响应具有重要的意义.反弯点和支座的间距随着λ增大而增大，但增长速率逐渐减小，此时梁体损伤趋于向碰撞位置处集中.

综上所述，支座反力对钢筋混凝土梁剪跨内最大负弯矩、跨中最大弯矩和反弯点位置均具有显著的影响，而以往的研究忽视这一部分的贡献，这会对钢筋混凝土梁内力的计算结果造成一定的误差.

3.3   负向支座反力和碰撞力峰值

图8为28组碰撞工况下支座反力和碰撞力峰值之间的散点图.其中，落锤冲击速度的范围取为1.7～13.7 m/s;跨高比取值范围为3.2～10.4.当跨高比为3.2时，上部支座并不会对构件产生约束作用.然而，当跨高比超过5.6时，不同碰撞速度下的负向支座反力近似与碰撞力峰值呈线性关系，并且两者的比值随跨高比的增大而增大.这与前面理论推导中关于支座反力和惯性力呈正比的假定一致，因此分别对不同跨高比时支座反力和碰撞力之间的关系进行线性拟合，拟合结果如图8所示.

为了研究跨高比对支座反力的影响，这里对计算结果进行拟合得到支座反力关于碰撞力峰值和跨高比的简化公式：

式中：R为支座反力合力（kN）;P为碰撞力峰值（kN）;l为构件净跨（mm）;h为截面高度（mm）.

冲击碰撞是一个极其复杂的物理问题，很难从理论上精确地确定碰撞力峰值的大小.本文通过对数值模拟得到的碰撞力峰值进行拟合来得到碰撞力计算公式.碰撞速度取值范围为1.7～13.7 m/s;碰撞质量的取值范围为50～1 600 kg;梁的跨高比取值范围为3.2～10.4.在局部响应阶段，梁内应力波从碰撞点逐渐向端部传播[16]，此时梁并不能全部有效地参与冲击响应.考虑到有效参与质量随波的传播而不断发生变化，准确地确定梁等效质量是比较困难的.不失一般性地，采用Biggs[23]提出的广义单自由度体系简化设计方法，其中梁的等效质量系数Km为：

式中：ρ为钢筋混凝土梁的线密度;？准（x）为梁的假定形状函数，这里假定？准（x）为线性分布，则悬臂长为 a、净跨为l的梁的等效质量系数Km = 1/3 + 8a3/3l3.从而得到4种不同跨高比梁的等效质量系数分别为：0.351、0.337、0.334和0.334.

考虑到冲击体与梁体的质量比和冲击体速度对碰撞力峰值的贡献最为显著，这里忽略了其他次要因素，对34组碰撞工况的数值分析结果进行多元非线性回归分析，从而得到碰撞力峰值P（kN）关于质量比Ms /meff、冲击速度v（m/s）的经验公式：

式（10）是基于落锤冲击试验的模拟结果所确定的，主要适用于本文所讨论的球形冲头低速冲击小尺寸普通钢筋混凝土梁的情况.碰撞力的拟合公式（10）可为前面的定性结论提供数据支持，以期进一步为其它碰撞工况提供理论参考.

图9给出了该经验公式的拟合优度.从数据统计结果可以看出，碰撞力峰值预测值和拟合值之比的平均值为0.998，变异系数为0.067，决定系数为0.951，可见拟合效果较为理想.

3.4   内力计算

将碰撞力峰值和支座反力的经验公式代入到梁的平衡方程中（如图6所示），可以得到冲击荷载下梁截面剪力和弯矩沿梁长度方向的分布情况，从而可以将梁的抗冲击性能设计转变为截面设计，便于工程应用.根据支座反力和碰撞力的经验计算公式可得负向支座反力合力与惯性力的比值为：

从而梁左半跨内任一截面的弯矩M和剪力V可以表示为：

瞬态响应阶段冲击荷载对钢筋混凝土梁的内力分布的影响远大于变形，因此取碰撞力达到峰值时的截面剪力和弯矩作为研究对象.图10对比了数值模拟和按式（12）（13）计算得到的不同碰撞速度和不同净跨长度时钢筋混凝土梁的内力分布.

总体来看，经验公式计算结果与模拟结果比较接近，只是在碰撞位置附近有一定的差异，这主要是由于在理论分析中将碰撞力简化为点荷载而未考虑碰撞接触面积所造成的.与弯矩分布相比，计算公式所得到的剪力分布更接近数值模拟结果.这恰恰是我们所期待的，因为在局部响应阶段梁的剪切效应比较明显，剪力对梁损伤的影响要远高于弯矩.这进一步表明了惯性力沿梁长度呈线性分布的假定是比较合理的.

4   结   论

本文采用数值模拟技术和理论分析方法对钢筋混凝土梁在冲击荷载下的局部响应特征进行了探讨.基于已有冲击试验验证了数值模拟方法的合理性，并分析了碰撞力、支座反力和内力分布的变化规律.根据荷载平衡原理得到了局部响应阶段梁内力的计算方法.主要结论如下：