用微元数值计算法研究行星椭圆轨道运动
朱佳平 林辉庆
(杭州市余杭高级中学,浙江 杭州 311100)
1 高中物理非线性问题
由于数学知识的限制,高中物理定量研究的问题,一般是物理量不随时间变化或随时间均匀变化的情况.高中物理还涉及很多的非均匀问题,在这些问题中,物理量随时间的变化不均匀,或者说,物理量的变化率不是常数.
对于非均匀问题,教科书一般只作定性介绍或直接给出结论.高中学生具有强烈的求知欲望,对于这些教科书中只作简略介绍的内容,他们迫切希望进一步了解其中的奥妙.例如,对于万有引力定律.
如何用高中学生能接受的方式研究非均匀问题,以满足学生的求知欲,是高中教学需要探讨的问题.
2 行星运动轨迹计算
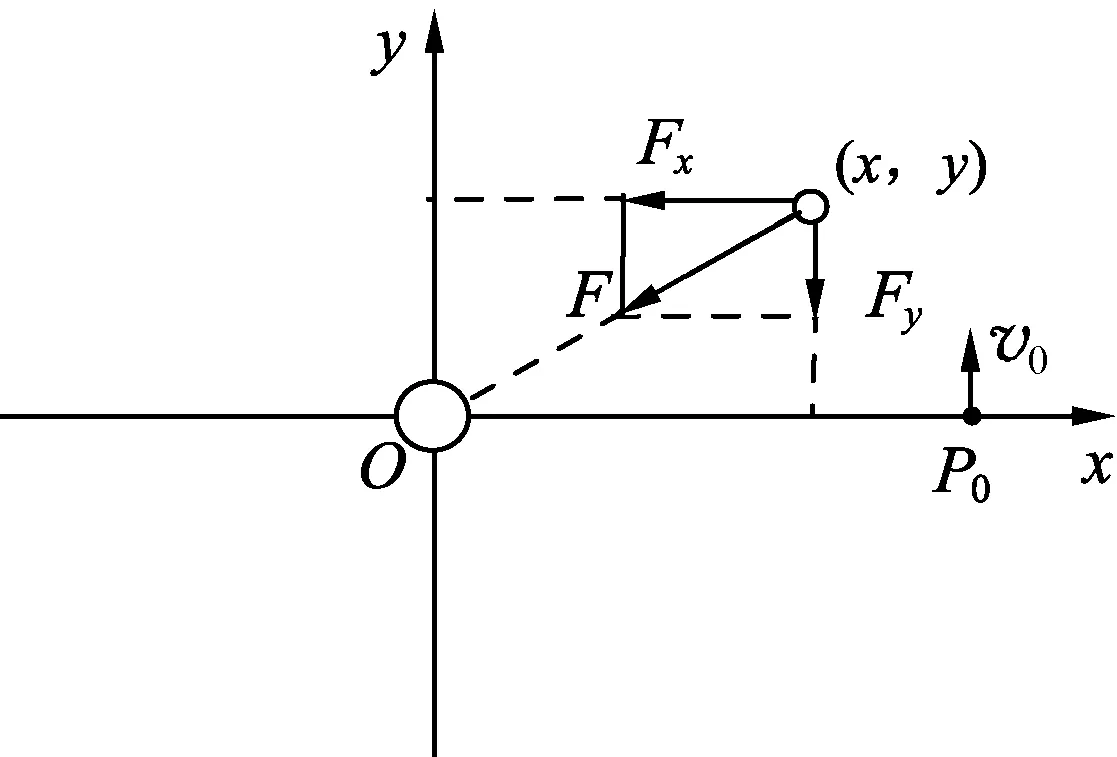
图1 行星收到太阳的引力
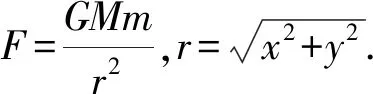
设行星在t=0时刻的位置为P0(x0,y0),速度为v0(vx0,vy0).在随后的一段很短时间Δt内,行星的加速度可以看作不变,它在x轴和y轴的分量分别为
(1)
在Δt时间内,行星在x轴和y轴的平均速度分别为
(2)
在t1=Δt时,行星运动到P1点,坐标为
(3)
在第2个Δt时间内,行星的加速度仍然看作不变,它在x轴和y轴的分量分别为
(4)
行星在x轴和y轴的平均速度分别为
(5)
在t2=2Δt时,行星运动到P2点,坐标为
(6)
同理可以求出t3=3Δt、t4=4Δt……行星的位置坐标.用这些数据就能在坐标平面上作出行星的运动轨迹.[1]
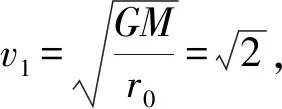
利用Excel的“插入散点图”即可画出行星运动轨迹如图2.可以看出此时行星的运动轨迹为椭圆,初始位置为近日点.
保持x0=0.500,y0=0,vx0=0和Δt=0.1不变,只要改变初速度vy0的数值,就可得到行星的初速度小于和等于“第一宇宙速度”v1、等于和大于 “第二宇宙速度”v2时的运动轨迹,它们分别是以初始位置为远日点的椭圆、圆、抛物线和双曲线.

表1 行星不同时刻的位置坐标
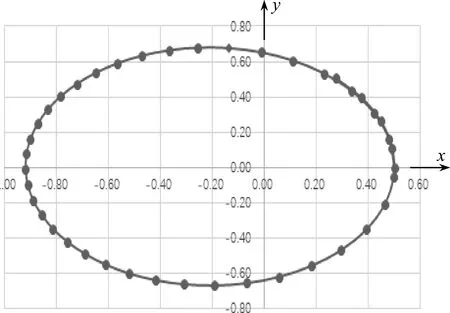
图2 行星的椭圆轨道
3 微元数值计算法
上述计算行星运动轨迹的方法叫作微元数值计算法.
微元数值计算法的要点有两个:一是通过取微元“化变为恒”.将一个随时间t作非线性变化的过程分割为很多个微小的过程,这样的微小过程叫作微元,微元的时间用Δt表示.在各个微元中,物理量可以看作均匀变化,即变化率可以看作恒定不变.二是数值计算.当已知了过程在t0=0时各个物理量的数值,由物理规律算出这些物理量在t0=0时的变化率.然后选取一个恰当的微元Δt的数值,由各物理量在t0=0时的变化率计算出它们在t1=Δt时的数值.由此又可以计算出它们在t1=Δt时的变化率和t2=2Δt时的数值……用这些数值就可以画出各物理量随时间的变化图线或任两个物理量之间的变化图线.[2]
可以看出,微元数值计算法的本质就是求积分,只是后者是Δt→0时的极限值,前者是近似值.由于我们在学校学习中所接触的物理问题大多是能用解析式“精确”描述的,解析式对物理过程的描述是理想化的,是真实过程的近似.在微元数值计算法中,可以靠减小微元的数值或取平均值的方法来减小误差,使结果的准确度达到我们的要求.
4 可行性、必要性与教学效果
4.1 可行性
通过高一物理第1章中瞬时速度概念和第2章中匀变速直线运动位移的学习,学生初步掌握了微元方法和极限概念,这为学习微元数值计算法打好了基础.
在技术上,学生在初中就已经掌握了Excel工作表的功能和用法,能用它处理数据和作图,这是用微元数值计算法研究问题的技术条件.
这样,只要知道一个非均匀物理过程的变化规律,就能借助于Excel工作表或信息技术中其他数据处理工具,用微元数值计算法求出这个过程各个物理量的具体变化情况.
4.2 必要性
真实的过程总是复杂的,绝大多数不能用函数的解析式描述.对这些问题的定量研究,都需要用微元数值计算法求得各个量在不同时刻的数值,描绘出它们随时间变化的图像.随着计算机运算能力的提升,用微元数值计算法解决实际问题的范围随之不断扩大,准确度不断提高.因此,微元数值计算法是实际生产和研究中常用的方法,高中学生有必要了解这种科学方法.
4.3 教学效果

用微元数值计算法求解复杂的非均匀问题,能极大地满足学生的求知欲,使他们深切地体验自然的奥秘和人类智力的伟大,从而增强探索自然奥秘的动力.
信息化是当今社会的主要特征之一.运用信息技术解决复杂物理问题的实践,能有效培养学生在生活、生产和研究中主动运用信息技术工具的意识和能力.

