基于学习进阶的教学构建
——以“速度变化快慢的描述——加速度”为例
应发宝
(北京市中关村中学,北京 100086)
1 设计思路
课程标准要求理解位移、速度和加速度.由于加速度概念的建立,思维跨度大,是教学的难点,所以在概念的建立过程中要建构学习台阶(如图1),放缓概念的建立过程,以进阶的方式降低难度,来突破难点.
通过生活、实验创设问题情景,用驱动性问题串线,以学生思考探索为主,教师引导、学生交互讨论为辅,让学生的学习一步步迈上更高的台阶.先让学生从生活实例中定性认识到,不同物体速度变化的快慢不同,启发学生用己学的物理量描述速度变化快慢,最后定义一新的物理量——加速度.教学设计从感性到理性,从定性到定量,体现概念学习的应有进阶意境,凸显“从生活走向物理,再从物理回归生活”的课程理念.

图1
2 教学过程
新课引入.
人口问题一直是国家发展的重大问题.自国家二胎政策于2016年1月1日起全面正式放开后,据说老大的生活状况发生了很大变化,如图2(b)(gif动态图).这说明人口问题也是每个家庭的问题,是值的每个人关注的社会问题.下面我们来看看(表1)北京市2006—2017年常住人口的数据统计.思考并回答如下问题:

图2

年份常住人口/万人20061601.020071676.020081771.020091860.020101961.920112018.620122069.320132114.820142151.620152170.520162172.920172170.7
驱动性问题1:哪“一年”人口变化最多?哪“一年”人口变化最快?哪“两年”人口变化最快?
驱动性问题2:由统计数据可知,人口的数目多少及人口数目的变化量都不能表示变化快慢,人口数目的变化快慢会与时间有关.那么物体运动速度的变化快慢,又会与哪些因素有关呢?
设计意图:由社会话题引入课题,即培养了学生学习兴趣,又引导学生关注社会问题.开门见山直接提出变化多少、变化快慢,直切主题.
台阶1: 认识生活中存在变速过程.

图3
播放视频(如图3): ① 中国飞人刘翔2004年雅典奥运会110 m跨栏起跑; ② 赛马沙土急停(原来赛马还带刹车功能); ③ 嫦娥一号发射开始阶段.
设计意图:先让学生认识生活中随处都存在变速过程.变速就是速度发生变化,会产生变化量.这一环节,即让学生了解研究变速运动的必要性,又引导学生迈向研究速度变化量的第二个台阶.
台阶2:研究速度的变化量.

图4
过渡语:我们该怎样计算一个物体的速度变化量呢?如图4所示,以射箭为例.(先介绍自制羽箭光电门测速装置:在箭杆的前端安装了约13 cm宽的挡光片,利用光电门传感器通过计算机就可以测出挡光板经过光电门时的速度.)
演示射箭创设情景1:通过DIS界面读出羽箭经过光电门的速度为15 m/s.
驱动性问题1:
(1) 羽箭从静止射出到15 m/s,速度变化量是多少?该怎样计算它的速度变化量呢?
(2) 羽箭速度从15 m/s到0射中靶的过程中,速度变化量是多少?又该怎样计算它的速度变化量呢?
设计意图:学生由于初中思维的惯性,会利用“大减小”很快计算出两种情景都为15 m/s的结果.
驱动性问题2:两个过程不同,结论相同,合适吗?如何处理才能在结果中体现过程的不同?
引导学生讨论:类比物体位置的变化(位移)等于末位置减初位置,所以物体速度的变化量也应是“末减初”,而不是“大减小”.实际上物理学中的所有变化量都是“末减初”.
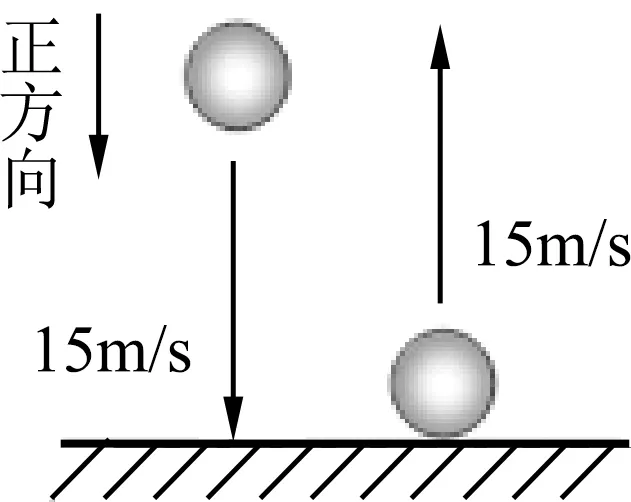
图5
演示弹力球碰撞创设情景2:弹力球垂直撞击水平桌面原速反弹.
驱动性问题3:如何计算弹力球碰撞前后的速度变化量?(如图5)
(学生很容易进入速度变化量是0的误区)
引导学生讨论:弹力球碰撞前后的运动方向明显发生了变化,速度变化量为0的结果说明“末减初”还是不行.原因是进行矢量计算时,方向很关键.我们可以类比同线二力合成的(矢量变标量计算)计算,应先在小球运动方向上选择一个正方向以此来确定速度符号,再来计算速度的变化量,结果中的符号含义表示与正方向的关系.因此,计算速度的变化量要先设运动正方向,再运用带方向的速度进行“末减初”.
设计意图: (1) 利用演示实验的真景实感将课堂保鲜; (2) 从羽箭射出、羽箭中靶再到小球原速反弹,3个情景层层递进,依次出现,通过问题驱动,让学生充分体验探究的过程;从学生原有的认知“大减小”到“末减初”,再到“带方向的末减初”,将“速度的变化量”逐步构建起来,即放缓了概念的建立过程,又逐步修正了学生的认知,最终形成正确的运动观.这样的教学可以使学生领悟到人们对事物的认识是逐渐深入其本质的,事物的发展过程就是“否定之否定”的过程.
过渡语:逻辑性强的计算法具有一定的信服力,但我们能否利用直观的作图法表示速度的变化量?

图6
驱动性问题4(图6):
(1) 如何利用作图表达速度、速度变化量的大小和方向?
(2) 如何从速度与速度变化量的方向关系来判断物体是加速或减速运动?
学生思考、讨论并小结:Δv与v0同向,物体做加速运动;Δv与v0反向,物体做减速运动.
设计意图:对于高一学生,刚刚接触矢量,如果不能很好地理解速度变化量的方向性,就会对加速度矢量的理解造成障碍,这是重难点突破的关键.在这一环节中,通过作图实践,不仅让学生进一步了解速度变化量的方向性,同时也为后面解决“根据加速度与速度的方向关系判断加速、减速”问题做好铺垫.
台阶3:比较速度的变化快慢.
演示鸡蛋落入烧杯创设情景3:命运不同的两颗鸡蛋.

图7
(介绍实验装置:如图7,横杆是为了保证两鸡蛋从同一高度静止释放;在鸡蛋的正下方放有两个烧杯,一杯空置,一杯装入3/4容积的水.)学生观察演示实验.
驱动性问题1:没碎的鸡蛋和碎的鸡蛋与烧杯的撞击过程有何不同?
学生思考讨论:鸡蛋没碎说明它与杯底碰撞的减速过程被水延缓了,即物体变速过程有快有慢.
驱动性问题2:如何比较不同物体变速过程的速度变化快慢?
(1) 理论定性探究.
驱动性问题1:能否用物体的运动速度大小来表示速度变化的快慢?
(推理:飞机匀速飞行,速度很大,但速度没变.)
驱动性问题2:我们要寻求一个新物理量来描述不同运动物体的速度变化快慢,它可能会与哪些因素有关呢(Δv、Δt、Δx)?(学生猜想)
师生活动:教师以米尺为单位,测高个学生的身高,大概1.5个单位;再以三角板为单位测量自己的身高,大概20. 5个单位(完美).这样测量公平吗?
引导学生讨论:要进行比较,就必须选取相同的标准来保证测量的公平性.〔宋〕朱熹“比者,以彼物比此物也.”“彼物”即为比较标准.
驱动性问题3:如何选取相同的标准?类比游泳比赛,相同的Δt或Δx比速度改变Δv(Δv↑,速度变化↑)或相同的速度改变Δv比Δt或Δx(Δt或Δx↓,速度变化↑)?一般选择哪种思维进行比较?(人们习惯正比思维)
驱动性问题4:根据人们的思考问题的思维习惯,一般选择正比思维,即相同的Δt(Δx)比速度改变Δv(Δv↑,速度变化↑).那Δt或Δx是多少会使比较更简单呢?(单位时间)
驱动性问题5:在实际的运动中时间或位移是任意的,不可能正好是1 s或1 m.单位时间或单位长度(如1 s或1 m),容易找到吗?(不容易)
驱动性问题6:由物体运动快慢(或人口变化快慢)类比启发,能否求出单位时间或单位长度的速度改变?
结论:“比值Δv/Δt(Δv/Δx)”表示单位时间(长度)物体的速度改变.比较“比值”,就相当于比较物体在不同时间段或不同位移段速度改变的快慢.因此,“比值”能够描述物体的速度变化快慢.
(2) 实验定量探究(Δv/Δt和Δv/Δx).
实验器材如图8(a)所示,数据记录表如表1所示.

图8
分组实验①:同一斜面、不同倾角、同一位置、静止释放小车(图8b,Δt=0.06 s).

表2
分组实验②:同一斜面、相同倾角、不同位置、静止释放小车(表略).
分组实验③:同一斜面、相同倾角、相同位置、不同大小或方向的初速度释放小车.
设计意图:为了防止学生质疑教师数据造假,现场使用打点计时器设计分组实验等效采集数据,每组准确地测出两种不同条件下的速度值,然后定量地比较这两情况下物体速度变化快慢的情况.
引导学生讨论:
对于同一特性的描述往往可以采用几种不同的方法,究竟哪一种定义方式为最佳?其中一项很重要的、很朴素的哲学判据就是伽利略基于“自然总是以最简单或最经济的方式运作”的不变量优先定义原则.在更多情形下定义结果表现为不变量的定义方式为最优先.



(3)v-t图像直观探究.
驱动性问题8:在分组实验①的v-t图9(a)中,哪条直线所代表的运动加速度更大?

图9
学生思考讨论:
线条①所表示的加速度更大,因为在速度变化量相同的情况下,它所用的时间更少.所以在v-t图像中,线条①的倾斜程度越大,所表示的加速度也越大.
① 速度均匀变化的变速直线运动.
小结:图像的倾斜程度(斜率).

加速度大小和方向都不变的直线运动——匀加速直线运动.
由分组实验②③的v-t图还知:加速度与速度(大小、方向)及初位置无关.
② 速度非均匀变化的变速直线运动——图像不是运动轨迹.
如图9(b)所示,运动过程中某一段时间速度变化的快慢程度——平均加速度;当Δt→0时,时间段就变成了时刻点.运动过程中某一时刻速度变化的快慢程度——瞬时加速度,即速度曲线某点切线的斜率.
(4) 实例应用:播放张培萌与高级教练机比赛视频.
高级教练机FTC2000G:最大平飞表速1000 km/h;最高时速1100 km/h.中国短跑世界冠军张培萌:百米速度10 s.
驱动性问题9: ① 飞机和张培萌最终谁快?用什么物理量描述?
② 短程启动阶段,谁的速度变化快?又用什么物理量描述?
设计意图:通过实例,让学生进一步清楚地认识到,速度、速度变化量、加速度是完全不同的物理量,3者没有必然联系.它们是从不同的角度描述物体的运动.
过渡语:下面请用物理加速度眼光来看世界,请用新的认知来描述生活中的现象.
台阶4:用物理加速度的眼光看世界.
① 自然界中的加速度.
播放:变色龙在捕食和水玉霉弹射孢子视频.
变色龙在捕食时的舌尖移动的加速度最高可达486 m/s2,相当于重力加速度的50倍;水玉霉弹射孢子时的加速度为(2-18万)g,时速高达90 km/h.
② 百姓生活中的加速度.
播放:早高峰十字路口绿灯放行时各种交通工具启动视频和发生车祸时制动视频.
交通管理部门为了交通安全,特制定了死亡加速度500g(g=10 m/s2)这一数值,以醒世人.意思是如果行车加速度超过此值,将有生命危险.那么大的加速度,一般情况下车辆是达不到的,但如果发生交通事故时(车辆碰撞时间大多为毫秒级),将会达到这一数值.
③ 人类科研中的加速度.
播放:科学家科研超重视频.
我们人类生理存受的加速度是有限的.科学家们为了研究加速度对身体的影响(生理效应),付出了很大代价.我们真的要感谢他们,是这些科学家的勇于探索和不断追求让我们对世界的认知越来越清晰.
设计意图:让学生知道物理每时每刻就在身边,随时随地都要遵守交通规则;让学生充分领会人类探索自然规律的科学奉献精神,同时也培养学生自主探究的意识和自信心.
小结:建立加速度的概念我们经历了如下过程,而在这个过程中我们又通过意义、单位、方向、运动性质等几个方面来理解了加速度[图10(a)].
本课结束语:总结本章知识脉络——描述物体的运动.
加速度是本章的最后一节,若进一步梳理本章的知识脉络能让我们更清楚地知道:描述物体的运动经历了怎样的过程,从参考系到加速度,我们的运动观不断地被更新,运动的描述也越来越完善.那加速度会变化吗?若加速度不变,这样的运动又会有什么样的特点呢?让我们在下一章揭开谜底[图10(b)].
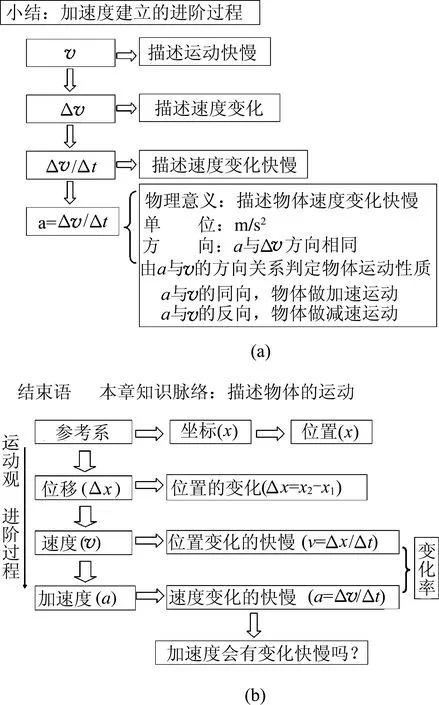
图10
在教学设计中应该把握住两种逻辑,即教材的“知识逻辑”(教什么)和教学的“思维逻辑(如何教).把握住“知识逻辑”,一方面是由于“知识传承”是学科教学目标中最为基础的内容;另一方面还由于在多维教学目标体系中的其他诸如“科学思维”、“科学探究”、“科学态度与责任”等目标都是渗透在“知识传承”过程中才能够实现和满足的.把握住“思维逻辑”,借助教学活动中清晰的思维逻辑线索和合理的逻辑结构,才能切实保障“知识传承”及多维教学目标体系中的其他目标得以实现.思维逻辑的进阶构建,学生才有可能深度学习.

