基于图论的多星综合任务规划双蚁群算法
柴伟杰,张 超
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
采用多个不同类型的遥感卫星,实施分布式观测,能够以多尺度的时间、空间和谱段分辨率获得多时段、多重空间覆盖、多谱段和多极化的目标特征信息。这些信息能够相互验证和互补,减少目标特征理解的不确定性,增加特征提取的全面性和精确性。通过适用的多源信息融合理论和技术,可达到对目标的综合感知,大幅度提高识别能力、定位精度能力。
多星综合任务规划是一个组合优化问题,其解的规模表现为问题规模(观测目标数量、卫星数量、地面站数量)的指数形式:一方面表现为对观测目标的选择问题;另一方面又表现为对观测行为的排程问题。其中,系统建模技术以混合整数规划[2]、约束满足模型[3-5]和图模型[6]为主,求解算法如蚁群算法[7-8]、遗传算法[9-11]和粒子群算法[12-15]等并行程度较高的亚启发式算法最为常见。GabrelV等人研究了单个卫星的多目标的日常规划问题,采用图论对问题进行建模,设计了2个阶段的方法来求解该问题,第一个阶段构造多条有效的路径,第二个阶段采用交互式算法选择较优的路径作为问题的解[16]。GLOBUS A比较了爬山法、模拟退火算法和遗传算法等几种优化算法[17]。Yu Chen综合了遗传过程与微粒子群过程,设计了多星调度混合算法[18]。
现有多星任务规划问题研究难以适应实际工程需要,没有考虑安排充电方案。本文基于图论理论构建了适合蚁群算法求解的独立集模型,综合考虑观测时间冲突约束、数传模式约束、指令模板约束、工作时间约束、文件下传约束和能源约束等因素,设计了双蚁群算法—第一支蚁群规划数传任务,第二支蚁群规划观测任务,为在轨运行的卫星制定合理的观测方案、接收方案和充电方案。
1 多星综合任务规划图论模型
1.1 多星综合任务规划问题
多星综合任务规划问题可以简要描述为:基于一组卫星、多种载荷、多个地面站、不同观测需求、对需要完成的观测任务分配执行时间和资源,考虑多种优化目标,给出优化后的多种任务安排方案,包括观测方案、数传方案和充电方案,如图1所示。
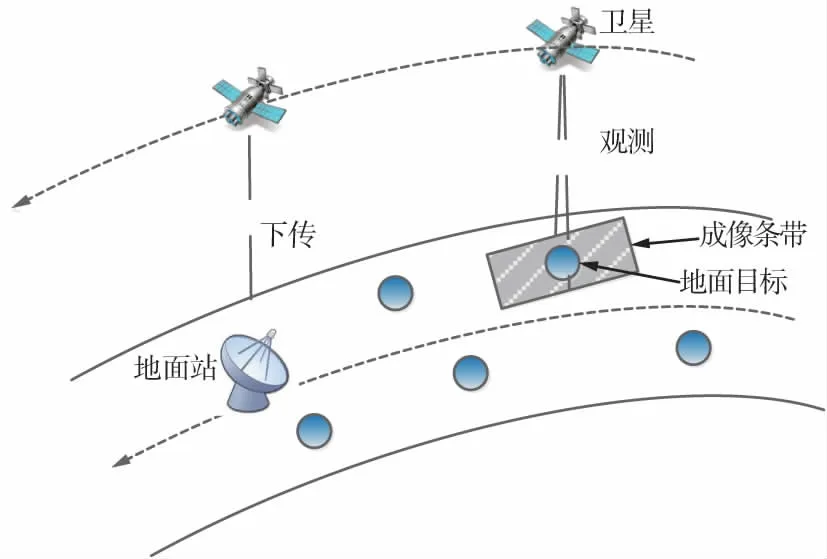
图1 卫星观测与下传示意图
卫星对地观测需要满足以下约束,如表1所示。
表1 约束与冲突表
下面对其中几个主要的约束进行具体介绍。
① 数传固存约束:卫星使用固存来存储数据,受到最大可存储容量限制,如果数据没有及时下传,将导致固存溢出的情况。
② 数传模式:考虑实传、记录、回放以及边记边放模式。
③ 指令模板冲突:卫星相机从一个角度状态变化到另一个角度状态的过程需要一定的时间间隔要求,为了使得前后2个成像任务都能够执行,前一个成像的结束时刻和后一个成像的开始时刻的时间差必须大于或等于它们的模板时间间隔要求。
④ 工作时间:由于卫星工作能力和能量的限制,卫星在单圈次内有一个最大观测时长约束。
⑤ 能源约束:当卫星蓄电池电量不足时,会影响卫星任务执行。所以考虑卫星的能量约束,将卫星充电作为应急任务安排在观测任务中。任务安排,首先检测卫星是否在阳照区,然后检测与后一个任务之间是否可以插入充电任务,如果可以,则安排充电。
约束处理流程如图2所示。
1.2 约束定义
约束①表示每个观测任务最多只能被执行一次,如式(1)所示:
(1)
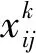
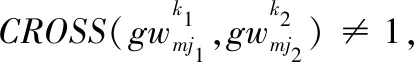
(2)
约束③表示如果卫星j先后执行2个观测任务,则卫星j需要有足够的姿态切换时间。
taskj(a+1).start≥taskja.end+l(taskj(a+1).id,taskja.id),
∀taskj(a+1).id>0且taskja.id>,
(3)
式中,taskja表示卫星j上执行的第a个任务;taskja.start表示第a个任务卫星j的执行开始时间;taskja.end表示第a个任务卫星j的执行结束时间;taskja.id表示卫星j对观测任务id进行观测。
约束④表示如果地面站m先后接收2颗卫星的下传数据,则地面站需要有一定的天线转换时间。
(4)
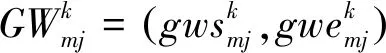
约束⑤表示卫星观测消耗的能量不能超过最大能量限制。
∀k∈{1,2,...,Noj},
∀j∈{1,2,...,NS},
(5)
式中,tdi表示目标i的观测时长;etj表示卫星j在单位时间进行观测或数据下传所需消耗的能量;Ej表示卫星j在单个轨道圈次内可消耗的最大能量。
约束⑥卫星执行观测任务之后,星上存储增加。
(cj(a+1)=cja+tctaskj(a+1).id,
iftaskj(a+1).id>0)
(6)
式中,cja表示卫星j在执行第a个任务后的星上存储;tci表示观测目标i所需消耗的卫星存储。
约束⑦表示卫星上所存储的数据不得超过星上存储器的最大容量。
cja≤Cj,∀j∈{1,2,...,NS},
(7)
式中,Cj表示卫星j的最大存储容量;cja表示卫星j在执行第a个任务后的星上存储。
1.3 图论模型
由时间窗和约束条件所转化的图是建立适宜蚁群算法求解的优化模型的基础,如图3所示。G=(A,E),A表示所有目标与卫星间时间窗集合和所有地面站与卫星间时间窗集合,E由A中点之间的冲突关系而构建,其中冲突关系包含3种:第一、由于模型待观测目标只需选择其和卫星间的一个时间窗进行一次观测即可,所以同一个待观测目标的不同时间窗存在冲突,即约束②。第二、同一颗卫星上的不同目标的时间窗之间存在执行时间上的冲突,即约束④。第三、不同卫星与同一地面站间时间窗存在执行时间的冲突,即约束⑤。
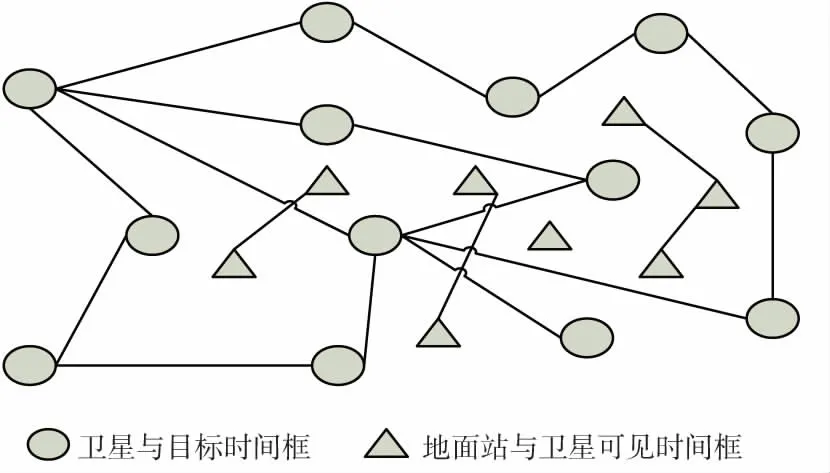
图3 任务冲突构造图
在预先规定的时间段范围内完成数量多的和权重总和综合较大的观测任务集合,也就是在图中寻找使得目标函数最大化的独立集,这就将所构造的任务冲突图转化为适合蚁群算法求解的独立集模型。卫星任务调度模型包括了观测任务和下传任务,还包括了能量的约束,采用双蚁群算法,首先第一支蚁群选择一个地面站与卫星间时间窗点,然后第二个蚁群在第一个蚁群选中的点基础上即确定的地面站资源前提下,选择目标与卫星间时间窗,紧接着第一支蚁群再次选择一个地面站与卫星间时间窗点和第二个蚁群再在已选地面站与卫星间时间窗点基础上选择目标与卫星间时间窗点,如此反复。在规划观测任务之前就已经规划了相应的下传任务,同时每颗卫星的每圈次能量值也是预先得知,即只需在规划观测任务时将下传任务和圈次能量看作成约束条件即可,将问题的模型转化为条件限制下的目标函数最大化的独立集问题。
2 基于双蚁群算法的多星综合任务规划
蚁群具有高度的社会性,蚂蚁之间大规模的协调行动中借助信息素(Pheromone)进行信息传递。蚂蚁觅食时,会在经过的地方留下信息素,后到的蚂蚁能够感知到这些信息素及其强度,选择信息素强度大的路径前进。针对研究问题的特点考虑过与问题相关的启发式信息,如:目标的剩余观测机会数量、目标的权重、目标的执行时间和观测机会的冲突度,下传机会间时间差等启发式信息来构成相应的启发式信息体系来引导蚂蚁,设计了2支蚁群分别释放意义不同的信息素来分别引导2支蚁群构建问题的解。
2.1 适应度函数
适应度函数考虑了已执行的观测任务数量占所有观测任务数量的比例,以及已执行的观测任务的权重之和占所有观测任务的权重之和的比例,调度目标是使它们的加权和最大化,其中,Rnum,Rwgt是比例系数。表达式如式(10)所示:
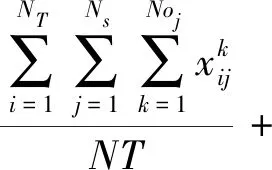
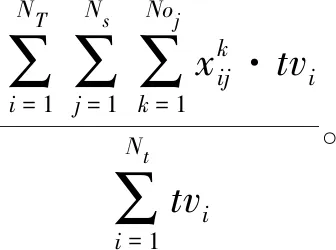
(10)
2.2 信息素更新规则
反复交替执行第一支蚁群和第二支蚁群的操作直到图中的下传机会节点为空为止,便可以得到问题的解,每只蚂蚁开始求解的过程都要首先初始化任务冲突图。每代蚂蚁完成求解后,采取全局最优解对蚁群进行更新信息素,如:式(11)、式(12)来分别对2支蚁群进行信息素更新,其中ρ为信息素挥发系数,Δτ为信息增量依据全局最优解计算而来,此外当发现新的全局最优解时采用式(13)来进行信息素更新。
τi(t+1)=τi(t)*(1-ρ)+Δτ(t),
(11)
Δτ(t)=Fitness(Sbest),
(12)
τi(t+1)=1/ρi∈(Sbest)。
(13)
2.3 局部搜索
局部搜索是从一个基础解出发搜索解的邻域的一种搜索方法,通过执行未观测目标的观测机会来替代已有解中已观测目标的观测机会,以及通过执行已观测目标的其他未执行观测机会来替代已有解中该目标已执行的观测机会使得未观测目标得以观测机会被观测,有效地提高了蚁群算法解的质量,同时蚁群算法接纳了质量更高的解的信息,通过对信息的利用为局部搜索提供更好的基础解,简言之蚁群算法和局部搜索相互交替,提高了整个算法的求解质量。局部搜索伪码如下:
步骤1:获得蚁群算法所得解S0,未观测目标的观测机会集合NA,已观测目标的未观测机会DA。
步骤2:while NA!= null
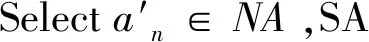
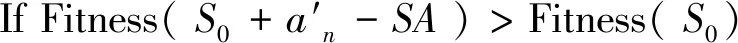
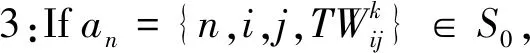
S0.Add(ap)and∃am={m,im,jm,
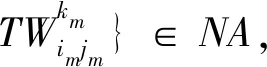
S0=S0-an+ap+am
2.4 算法流程
基于双蚁群算法的多星综合任务规划算法流程如图4所示。
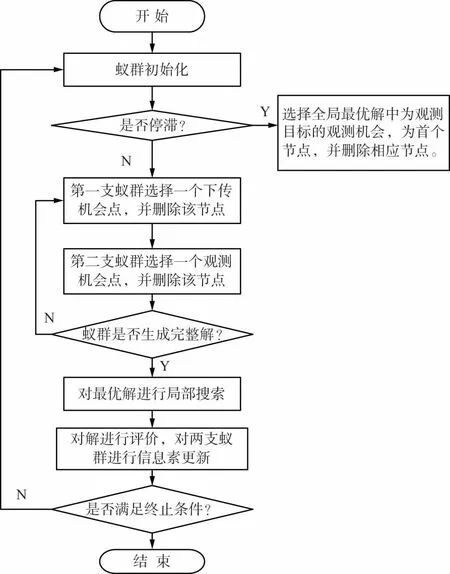
图4 双蚁群算法流程图
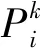
第二支蚁群规划观测任务,选择相应的观测机会点即目标与卫星间的时间窗,将信息素τi释放在图中的观测机会节点之上,即τi表示了蚁群选择编号为i的观测机会执行相应目标的观测任务的“知识积累”。和第一支蚁群类似,第二支蚁群中第k只蚂蚁选择观测任务节点时根据式(14),其中的candidate表示在任务冲突图中,与部分解没有连线的候选观测机会点集合A2。当蚂蚁选中一个节点,首先进行能量约束即约束⑥判断,如果不满足能量约束,则在任务冲突图中以及在A2中删除该点,并重新进入从A2中选择节点的计算,如果满足能量约束,则进入存储约束即约束⑦判断,当其不满足约束⑦,则在A2中删除该点,并重新进入从A2中选择节点的计算,当其满足约束⑦,则该节点成功插入到部分解中,并在任务冲突图和A2中删除与该点有连线的点包括其自身。直到A2无点可选,则重新进入第一支蚁群的运算,开始新的下传机会节点选择。
由式(10)可以看出,本算法只依靠信息素来引导蚂蚁进行求解,而没有利用与问题本身有关的启发式信息。在研究本算法过程中,考虑过与问题相关的启发式信息,如:目标的剩余观测机会数量、目标的权重、目标的执行时间和观测机会的冲突度,下传机会间时间差等启发式信息来构成相应的启发式信息体系来引导蚂蚁,然而由于问题的复杂约束造成了启发式信息不具有前瞻性,使得算法快速的收敛易陷入局部优,并没有提高解的质量,反而由于计算相应的启发式信息而导致算法运行时间的增加。
(14)
3 实验仿真及结果分析
为了验证算法性能,采用C#语言在Windows7操作系统下开发了原型软件,利用美国Analytical Graphics公司开发的卫星工具包(Satellite Tool Kit)随机生成卫星、地面站和点目标、区域目标测试数据。其中卫星数量为2个它们的轨道建立参考了资源三号、高分一号,地面站按照大三角布局密云(40.369 7°,116.843 0°)、三亚(18.243 1°,109.505 0°)、喀什(39.454 7°,75.979 7°),按目标数量50,100,150,200生成4批数据,测试过程分别对各批数据进行了10次测试。双蚁群算法由于采用双信息素表示目标和地面站信息。因此,对各个参数设置如下:蚁群数量均设置为10,观测目标的蚁群α、ρ参数分别设置为0.2、0.2,规划下传任务的蚁群α、ρ参数分别设置为0.5、0.3,最大迭代数设置为100。仿真实验结果如图5所示。
并根据统计学中位数原理,利用目标函数值统计中位数与遗传算法算法、量子遗传算法进行比较如图6、图7所示。其中,对遗传算法的4个参数设置如下:种群规模200、交叉概率0.9、变异概率0.1、迭代次数100。
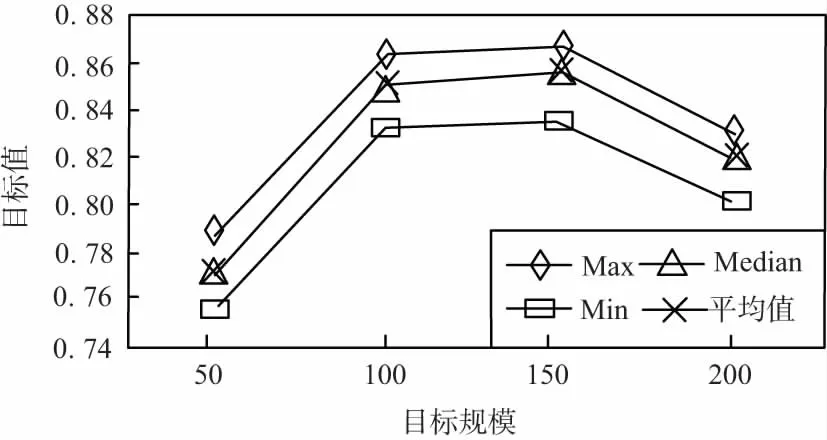
图5 双蚁群算法仿真实验结果
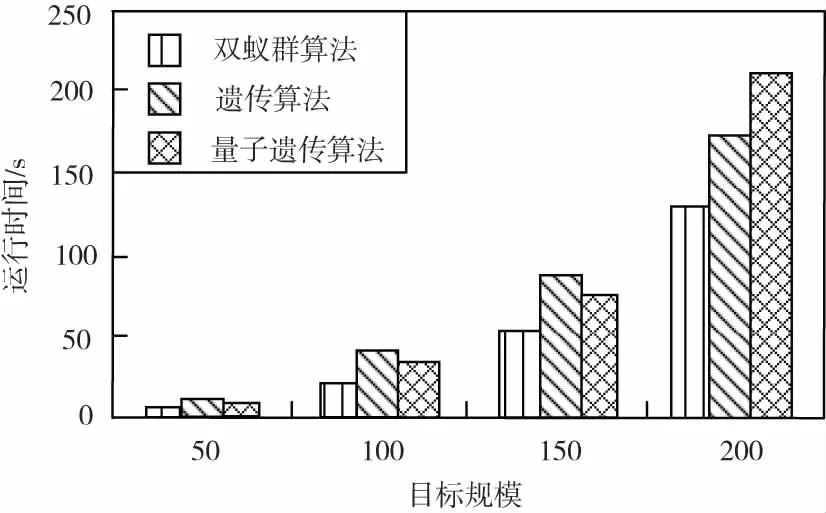
图6 双蚁群算法运行效率分析
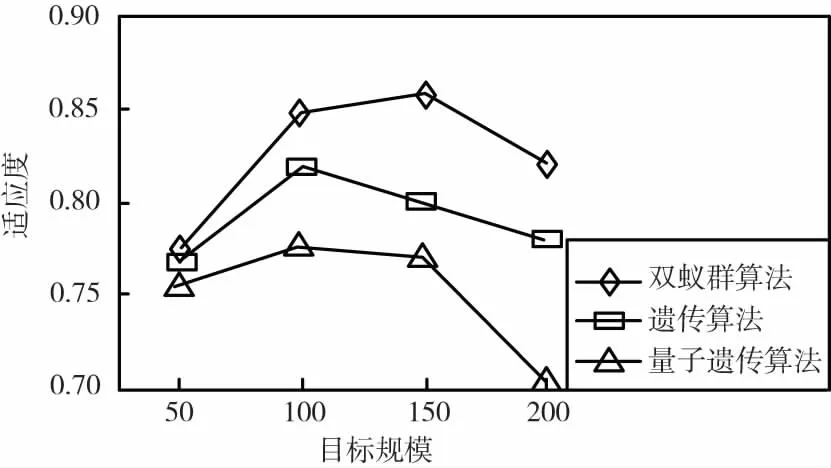
图7 双蚁群算法优效性对比分析
结果分析:双蚁群算法一方面针对问题解空间较大方面,通过采取较大的挥发系数ρ和全局最优解,以及当发现新的全局最优解通过式(16)进行信息素更新,使得问题的解能够有效的收敛。另一方面为了避免算法陷入局部优,在求解下一代解中从全局最优解中未观测目标的观测机会点集合中随机选取一个点作为首个插入到解中的节点,并在任务冲突图中删除与之连线的节点,这样增加了解的多样性的同时也保证了解的质量,因为只有未观测目标可以得到相应的观测机会,才有可能提高解的质量,此外通过局部搜索帮助蚁群跳出局部优也提高了解的质量。
4 结束语
本文针对求解多星对地观测任务规划的工程化应用,设计了新的双蚁群算法,给出了对应的适应度函数、信息素更新规则和局部搜索机制,创新性地将卫星充电作为应急任务在观测任务中进行插入。基于设计进行了算法求解仿真实验,对算法的求解特征及求解规划问题的适应性进行了实验分析。下一步的主要工作是进一步完善底层算法,引入机器学习机制,建立多星对地观测任务规划基本调度策略。

