待定系数法求函数 y=Asin（ωx+φ）+K 的解析式

■杜红全 黄海虹

由三角函数的图像求函数y=Asin（ωx+φ）+K 的解析式，关键是确定参数A，ω，φ，K的值。下面举例说明用待定系数法求函数y=Asin（ωx+φ）+K 的解析式的方法与技巧，供大家参考。

例已知函数y=Asin（ωx+φ）+K的最小正周期为T，且在一个周期内的图像如图1所示，求此函数的解析式。

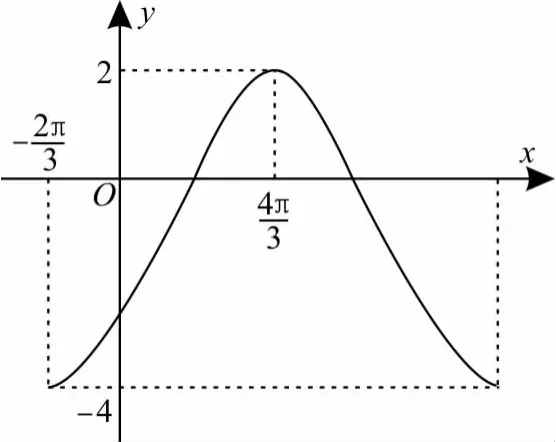
图1

解：由图像可知函数的最大值为2，最小值为 -4，所以由图像可知所以T=4π。由可得此时

下面介绍求φ值的几种方法。

方法1：（代入法）把最高点的坐标代入可得所以Z），解得因为|φ|＜所以故所求函数的解析式为

方法2：（五点法中的“第二点”）由图像可知点为五点法中的“第二点”（即图像的“峰点”），所以把代入ωx可得所以φ=故所求函数的解析式为y=

方法3：（五点法中的“第三点”）设“第三点”的横坐标为x，由于“第三点”与“第二点”之间的距离为函数的周期，且周期T=4π，所以解得把ω=代入ωx+φ=π，可得π，所以故所求函数的解析式为

方法4：（五点法中的“第四点”）设“第四点”的横坐标为x，由于“第四点”与“第二点”之间的距离为函数的半个周期，且周期T=4π，所以解得把代入可得所以故所求函数的解析式为