一类具有脉冲扰动和饱和治愈率的媒介传染病模型研究
董红森,张素霞
(西安理工大学理学院,陕西西安710054)
一直以来,人们面临着各种传染病的威胁,这些传染病一般都是通过细菌、病毒、真菌等引起的,直接感染动物或者人,被感染的动物或人在人与人、动物与动物或人与动物之间相互传播。媒介传染病是通过某种生物载体进行传播的疾病,如以蚊子作为传染媒介,常见的传染病有登革热、疟疾和西尼罗河热等。在这些疾病的传播过程中,被感染的蚊子通过叮咬健康的宿主而将病毒传染给人群,同时健康的蚊子在叮咬被感染的宿主时获得病毒,如此交替循环从而引起此类媒介传染病的传播和蔓延。
传染病动力学模型是研究疾病传播规律的一种有效的方法。针对传染病的特点利用数学模型对其传播过程和传播机理进行研究,以寻求合理高效的疾病管理方法和控制措施。在对媒介传染病研究的过程中,一些学者通过建立不同形式的数学模型来描述疾病发生、发展及控制特点,取得了丰富的研究成果[1-4]。为了研究实施脉冲扰动对管理和控制疾病的影响,脉冲微分方程模型近来被广泛利用,以更准确地描述疾病传播和控制的客观情况[1,4-6]。随着现代医学的发展,医疗技术和医疗水平有了长足的进步,人们对疾病的治疗和管理水平也随之得到显著提高,其治疗程度也被刻画到传染病动力学模型中[7-9]。本文将考虑对媒介实施脉冲控制并对宿主进行饱和治疗的SIR-SI媒介传染病模型,分析脉冲控制周期和强度以及饱和治愈率对模型动力学性态的影响。
1 模型建立
将宿主(人群)划分为三个仓室:易感者类、染病者类和恢复者类,设SH(t)、IH(t)和RH(t)分别表示在t时刻宿主中易感者、染病者和恢复者的数量。将媒介(蚊子)划分为两个仓室:易感者类和染病者类,SM(t)和IM(t)分别表示t时刻媒介中易感蚊子和染病蚊子的数量,从而建立媒介传染病模型:
(1)

由于蚊子相对于人的生存时间较短,这里不考虑蚊子的因病死亡,并假设模型中的参数都是非负的。
2 无病周期解的存在性与稳定性
当宿主和媒介中无病毒存在,考虑式(1)的无病子空间:
Xs={(SH,IH,RH,SM,IM):SH≥0,IH=0,RH=0,SM≥0,IM=0}
则有:
(2)
由于只对媒介实施脉冲控制,即式(2)中关于易感宿主的微分方程无脉冲扰动,则当t→,
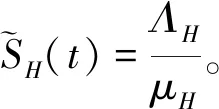

(3)
计算易得该脉冲方程在时间段(nT,(n+1)T]内的周期解为:
由式(3)中第二个等式得:
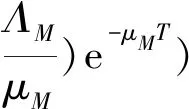


即



并将变换代入式(1),由线性近似可得脉冲微分方程组:

其中:
Q(t)=

为方便计算,令
其中:

其中ΦF-V(t)为x′(t)=(F-V)x(t)的基解矩阵。由于|μH|、|μM|都小于1,则谱半径r(P1eUT)<1。

定义阈值:R0=r(P2ΦF-V(T)),R0表示一个感染者单位时间内传染人数,或者表示一只感染蚊子单位时间内传染蚊子的数量[12]。
3 疾病的持久性
定理2如果R0>1,疾病一致持久,即存在正整数η>0,使得:


(4)
考虑如下系统:
(5)

由比较定理[11],存在t2>t1,ε2>0,对任意的t>t2有:

(6)
考虑系统:
(7)
式中u=(u1,u2)。式(7)的解可表示为u(t,nT,u(nT+))=ΦF-V(t-nT)u(nT+),则u((n+1)T+)=PΦF-V(t-nT)u(nT+)。当R0>1时,随着t→,u1→且u2→,则,
以下讨论两种可能情况:
情况一t足够大时,Ii(t)>η,i=H,M;
情况二t足够大时,Ii(t)值在η处波动,i=H,M。

从而得:
IH(t)≥IH(t1)e-(α1+μH+r+dH)(t-t1)≥
ηe-(α1+μH+r+dH)(t-t1)≥ηe-(α1+μH+r+dH)(n2-n1+1)T
对IM有:
IM(nT+)=(1-p)IM(nT),t=nT,n∈N
可得:
IM(t)≥η(1-p)n2-n1e-μM(t-t1)≥
η(1-p)n2-n1e-μM(n2-n1+1)T
令η1=min{ηe-(α1+μH+r+dH)(n2-n1+1)T,
η(1-p)n2-n1e-μM(n2-n1+1)T},因为n2-n1>0,所以η1>0有界,于是当t∈[t1,t2]时,Ii(t)≥η1>0,i=H,M。当t>t2时,同样存在非零的正整数η2,如此下去可得到序列{ηj},j=1,2,…,k,…,其中:
ηk=min{ηe-(α1+μH+r+dH)(nk+1-nk+1)T,
η(1-p)nk+1-nke-μM(nk+1-nk+1)T}
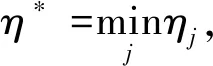
4 数值模拟
为了进一步研究模型的动力学性态,在一定的参数取值下,主要以脉冲强度p和脉冲周期T为控制参数对系统的数值解、时间序列图和分支图分别进行数值模拟。
4.1 脉冲控制周期T的影响
模型中参数取值分别为:ΛM=1 300、ΛH=2.1、βM=0.16、βH=0.88、μM=0.029、μH=0.005、c=0.3、dH=0.08、r=0.005。式(1)的初始值分别取为:SH=100、IH=0、RH=500、SM=300、IM=10。在α1=6,α2=3以及α1=7,α2=4两种不同饱和治愈率情况下,研究脉冲控制周期T对系统动力学性态的影响。图1和图2展示了当脉冲强度p=0.85且脉冲控制周期T在一定范围内取值时,式(1)中各变量的变化情况。
在上述参数取值下,对比图1和图2可以看出,两种不同饱和治愈率下模型出现不同的性态,并且两种情况下系统都具有丰富的动力学行为。以图2(b)为例,当p=0.85,α1=7,α2=4时,出现带有周期窗口的混沌带→倍周期分岔→周期吸引子→混沌→含有周期窗口的混沌带→周期解分支。当参数T的取值在[40, 40.9]之间时,系统进入一个带有周期窗口的混沌区域,特别是参数T的取值大于40.178时,混沌突然消失,出现一个周期窗口。参数T的取值增加到40.9时,因为系统周期解失去稳定性,系统进入到混沌状态,当参数T的取值增加到43时,混沌突然消失,系统再次进入平衡状态。同时由图2(a)可以看到,随着参数T取值的增加,易感人群的最大量是非单调变化的。图3和图4进一步给出了染病媒介和染病宿主的变化情况。由图3(a)可以看出,当T=40.5时,IM随时间呈现出3T周期变化,对应的图3(b)呈现3T周期吸引子的分岔行为。同样,由图4 (a)可以看出,当T=40.5时,染病者IH随时间也呈现周期变化,图4(b)为对应的周期吸引子分岔行为。

图1 当脉冲强度p=0.85,α1=6,α2=3,以脉冲周期为分支参数时式(1)中变量的分支图Fig.1 Bifurcation diagrams of system (1) with respect to bifurcation parameter T when p=0.85, α1=6 and α2=3

图2 当脉冲强度p=0.85,α1=7,α2=4,以脉冲周期为分支参数时式(1)中变量的分支图Fig.2 Bifurcation diagrams of system (1) with respect to bifurcation parameter T when p=0.85, α1=7 and α2=4

图3 脉冲周期T=40.5,式(1)中染病媒介IM的时间序列图以及相应的解轨线Fig.3 When T=40.5, a numerical solution of system (1) about vectors as time tending to infinity and the corresponding trajectory

图4 脉冲周期T=40.5,式(1)中染病宿主IH的时间序列图以及相应的解轨线Fig.4 When T=40.5, a numerical solution of system (1) about infected hosts as time tending to infinity and the corresponding trajectory
4.2 脉冲强度p的影响
当参数与初值的选取与4.1中相同,同样在α1=6,α2=3以及α1=7,α2=4两种情况下研究脉冲强度p对系统动力学性态的影响。当脉冲控制周期T=45时,以p为分支参数,式(1)中各变量的动力学性态如5图和图6所示。

图5 脉冲周期T=45,α1=6,α2=3时,以脉冲强度p为分支参数时式(1)中变量的分支图Fig.5 Bifurcation diagrams of system (1) with respect to bifurcation parameter p when T=45, α1=6 and α2=3

图6 脉冲周期T=45,α1=7,α2=4时,以脉冲强度p为分支参数时式(1)中变量的分支图Fig.6 Bifurcation diagrams of system (1) with respect to bifurcation parameter p when T=45, α1=7 and α2=4
由图5和图6可以看出,两种不同饱和治愈率下脉冲强度都对系统有重要的影响,出现了丰富的动力学性态。
以图6(b)为例,当T=45,α1=7,α2=4时,出现周期分岔→带有周期窗口的混沌带→倍周期分岔→周期吸引子→混沌。当p的取值在[0.8, 0.880 4]之间时,系统一直处于周期分岔阶段,当脉冲强度p的取值大于0.880 4时,系统进入混沌状态。当脉冲强度p的取值在[0.880 4,0.92]之间时,系统进入了一个带有周期窗口的混沌区域。当脉冲强度p的取值大于0.909 8时,混沌突然消失,出现一个周期窗口。
另外,由图6(a)可以看出,随着脉冲强度p取值的增加,易感人群的最大数量是非单调变化的。
图7和图8给出了p=0.91时染病媒介IM和染病宿主IH的变化情况,对应于图6中两个变量的分支图。
由图7(a)可以看出,当p=0.91时,IM随着时间变化呈现出倍周期变化,对应的图7(b)出现5T周期吸引子的分岔。
由图8(a)可以看出,当p=0.91时,IH随着时间变化呈现出倍周期变化,对应的图8(b)呈现5T周期吸引子的分岔行为。脉冲强度p的取值增加到0.917 8时,因为系统周期解失去稳定性,系统又直接进入了混沌区域。
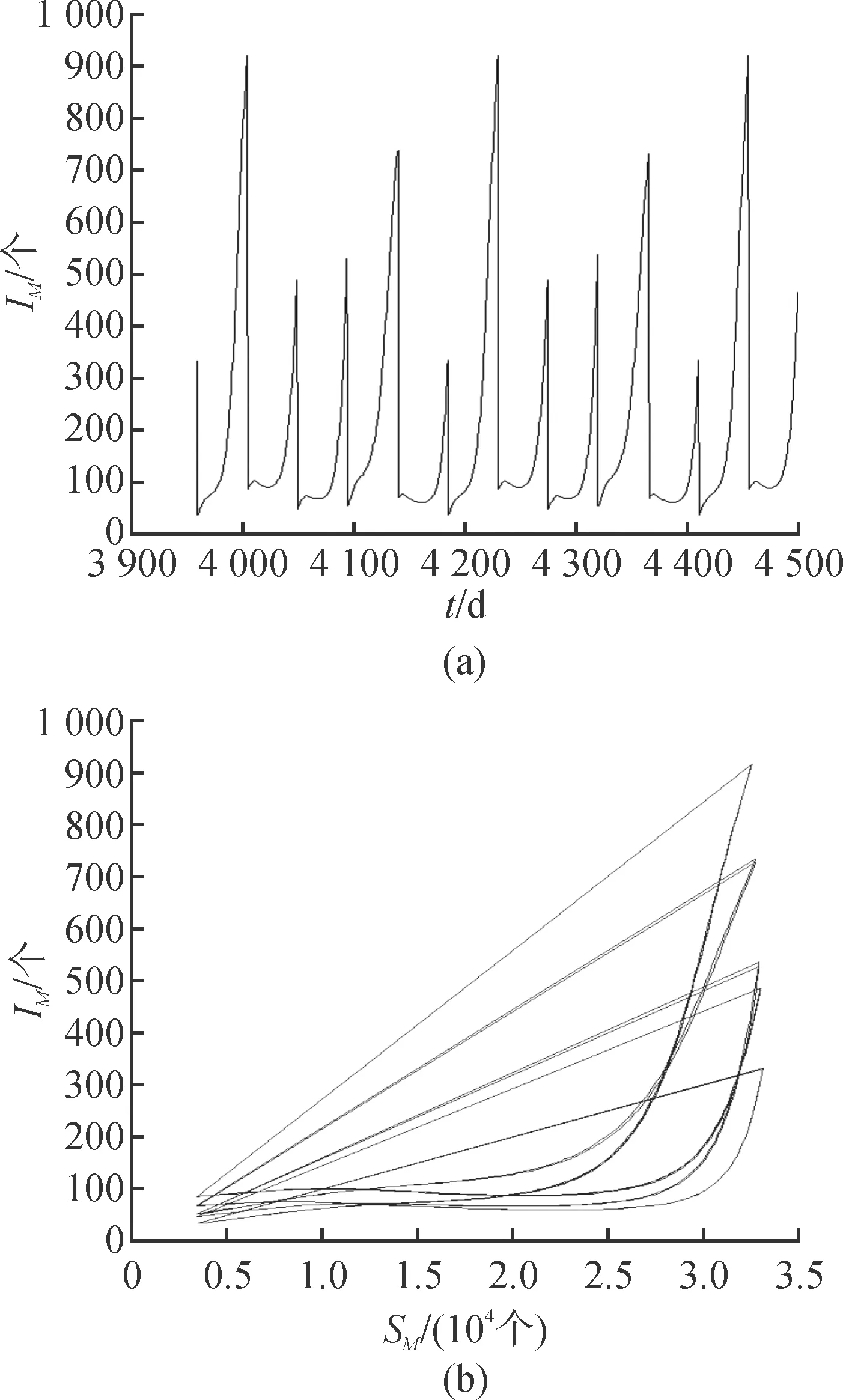
图7 脉冲强度p=0.91时,式(1)中染病媒介IM的时间序列图以及相应的解轨线Fig.7 When p=0.91, a numerical solution of system (1) about vectors as time tending to infinity and the corresponding trajectory

图8 脉冲强度p=0.91时,式(1)中染病宿主IH的时间序列图以及相应的解轨线Fig.8 When p=0.91, a numerical solution of system (1) about infected hosts as time tending to infinity and the corresponding trajectory
5 结 语
本文通过建立一个SIR-SI媒介传染病模型,研究了固定时刻脉冲控制下系统的动力学性态。利用脉冲微分方程理论分析了模型无病周期解的存在性与稳定性,并定义出模型的阈值,即基本再生数,然后利用比较定理证明了当阈值大于1时疾病的一致持久性。同时,通过选取适当参数,对模型的动力学性态进行了数值模拟。主要以脉冲强度p和脉冲周期T为控制参数对系统的数值解、时间序列图和分支图分别进行了数值分析,同时也对比了不同饱和治愈率下系统各变量的分支变化情况。利用本文模型的理论和数值研究结果,可以为控制相关媒介传染病的流行和传播提供参考。

