八连杆抗冲击隔离器设计与性能分析
高 鹏,闫 明,温肇东,张 磊
(1.沈阳工业大学 机械工程学院,沈阳 110870;2.海军装备研究院,北京 100161)
舰艇惯性导航设备能够为其提供速度、姿态及位置信息,是保证舰艇正常运行的关键设备。对于舰艇来说,水下非接触爆炸一般不会击穿船体结构,却会造成电子设备的大范围的破坏,导致舰艇丧失战斗力[1-3]。由于惯性导航设备属于高精密仪器,在水下非接触爆炸冲击环境中,会使其导航精度下降,甚至丧失导航能力,故除提高舰艇本身的抗爆抗冲击能力外[4],对惯导设备进行有效的冲击防护也尤为重要。面对冲击环境的复杂多变,要求惯导设备的抗冲击隔离器需具有以下特点,首先,能够抵御来自任意方向的冲击载荷;其次,具有静态刚度高的力学特性,在受到小幅冲击载荷时,能够相对舰艇处于静止状态;最后,在保证转角精度的同时,隔离器具有较好隔离率,能够卸载冲击载荷,从而保证惯导设备正常工作。
欧美国家对惯导设备冲击防护的研究起步较早,美国Langley研究中心于20世纪末采用了准零刚度技术为航天飞行器研制的隔振器,对于振动和冲击具有理想的隔离能力[5];美国智能自动控制公司为舰载飞机发动机制作的隔振器,能够保证在正常飞行期间减小其发动机振动幅值,为稳态飞行、着陆时抵抗冲击提供最佳参数[6];澳大利亚目前正在研究的将混合式主动隔离技术,以此来减小冲击、振动[7];我国在抗冲击隔离器研发方面,也取得了一些成果,包括研制了截止激励抗冲隔离器、六杆杆隔离器等。
冲击响应属于瞬态运动,主动、半主动控制需要一定的反应时间和外部动力,故被动式隔冲应用较为广泛[8]。所设计的八连杆抗冲击隔离器属于被动式隔冲器,是多环一次闭合并联结构,具有抗冲击能力强等优点,其结构的对称性解决了六杆结构横、纵向刚度不一致的问题,提高了隔离器在复杂环境中的抗冲击能力。通过多体动力学ADAMS软件[9],对比分析了六、八连杆的水平向抗冲击能力,并仿真分析了冲击载荷及阻尼参数变化对八杆结构抗冲击性能的影响,进一步计算了隔离器在不同冲击载荷下的隔离率,并利用500 kg双波冲击试验机对隔离器进行试验验证。进一步得到结论,多杆并联隔离器的结构分析和抗冲击特性研究对精密设备的冲击防护具有重要意义。
1 结构设计及工作原理
1.1 结构设计
八连杆抗冲击隔离器结构主要由8根隔冲杆、设备安装板、基座、上、下铰链结构组成,其中为满足隔离器转角精度的要求,将连接部件设计成具有高精度和高强度特性的球形铰链结构。
其中单根隔冲杆结构主要上、下球铰、推杆、限位结构、导杆、弹性元件组成。由如图1所示,其工作原理为:假定向下为正方向,当冲击方向为正向时,推杆向下运动并压缩弹性元件,一定压缩量后弹性元件回弹,使推杆反向运动,回到初始位置后进一步带动导杆共同沿反向运动,当弹性元件到达限位结构时,弹性元件上端停止运动,导杆底部挤压弹性元件下端使其向上运动,导致弹性元件再次被压缩,到达极限压缩量后,弹性恢复力使导杆向下运动,同时带动推杆一起运动,周而复始,进行冲击隔离,其中弹性元件始终处于压缩状态。

图1 单根隔冲杆结构Fig.1 Single isolated structure
八连杆隔离器整体结构如图2所示,为达到隔离器能够抵御任意方向冲击载荷的要求,将每2个隔冲杆设定成一组抗冲击结构,共4组,沿横、纵向对称布置,并均按其端部夹角60°安装,由此可分别沿垂向、横向及纵向卸载任意方向的冲击载荷。
由于整体结构的特殊性,降低了隔离器高度,扩大了八根隔冲杆所围成的内部空间范围,同时为了降低系统体积和设备的重心,提高系统利用率,将用于模拟设备的质量体反向安装至隔离器内部。

图2 整体结构Fig.2 Whole structure
基于惯导设备对静态刚度高的要求,需对隔冲杆内部弹性元件进行预紧,根据惯导设备的相关标准,设定预紧力为F0,且F0大于所承载的重力,因此当系统没有受到冲击作用时,弹性元件不发生变形;当系统受到振动载荷时,由橡胶片进行隔振;当系统受到冲击载荷F,且F≤F0时,弹性元件不发生变形,冲击载荷F通过隔冲杆内部橡胶片缓冲后作用到被隔离设备上,由于冲击力小于设备允许承受的极限冲击力,因此可保证设备安全运行;当F>F0时,弹性元件发挥缓冲作用。
1.2 横、纵向隔冲原理对比分析
基于传统六连杆结构横、纵向刚度不一致以及相邻隔冲杆组间角度过大导致弱项杆组不能完全发挥作用的问题,所设计的隔离器在杆组数量及结构对称性方面做出了适当的改善。如图3所示,左、右两组图分别为六杆、八杆结构的三维以及横、纵向隔冲原理图。杆组在水平向上的隔冲夹角分别为120°、90°,F为来源于任意方向的瞬时冲击载荷。
分别对两种结构的横、纵向隔冲原理进行分析,图3(a)中,六杆结构的C向杆组将承受主要冲击,而A、B向杆组为弱项杆组,即C向杆组发挥主要隔冲作用,而弱项杆组A、B则按照冲击角度的差异分别承载大小不同的冲击载荷,其中


(a) 六杆结构(b) 八杆结构
θA+θB= 120°
(1)
当θA>θB时,弱项杆组B将承受更多瞬时载荷,同理当θA<θB时,杆组A将承受更多瞬时载荷,即杆组A、B所承受的载荷大小与其相隔冲向和冲击向的夹角成反比。由此可见,瞬时载荷的分配不均匀性降低了隔冲杆组的利用率。
而在八杆结构中,由于4组隔冲杆为对称布置,故其横、纵向刚度具有高度的一致性,且
θD+θE= 90°
(2)
即杆组与冲击方向的夹角范围更小,提高了载荷分配的均匀性,实现了在复杂冲击环境中,隔离器可沿垂向、横向、纵向对来源于任意方向的冲击载荷进行缓冲隔离。
1.3 机构自由度分析
(3)
并不适于多自由度、多环的空间机构自由度计算,故将以螺旋理论[10]为基础,通过反螺旋自由度原理计算八连杆结构的自由度。
八连杆结构为对称的多环一次闭合并联结构,共有8个分支,所有分支的上端与动平台发生闭合,下端与静平台发生闭合。
图4中每个分支(隔冲杆)中间为移动副,两端均为球面副,故单根隔冲杆的螺旋系为
$S1=(1 0 0 ;0 0 0)
$S2=(0 1 0 ;0 0 0)
$S3=(0 0 1 ;0 0 0)
$p1=(0 0 0 ;d1e1f1)
$S4=(0 1 0 ;d4e4f4)
$S5=(1 0 0 ;d5e5f5)
$S6=(0 0 1 ;d6e6f6)

图4 单独分支螺旋系Fig.4 Single branched helix system
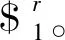
假定上、下球铰为限制绕隔冲杆轴线转动的球销结构,则单支隔冲杆螺旋及反螺旋系如图5所示,其螺旋系可表示为
$S1=(0 1 0 ;0 0 0)
$S2=(1 0 0 ;0 0 0)
$p1=(0 0 0 ;e1d1f1)
$S3=(1 0 0 ;e3d3f3)
$S4=(0 1 0 ;e4d4f4)

图5 单独分支螺旋及反螺旋系Fig.5 Single branched helix and reverse helix

(4)
(5)
分别对机构的自由度进行求解验证,其中式(4)中的d=6-λ=5。
由式(4)得到
式(5)中过约束u应等于平台承受反螺旋的总数与对应独立的反螺旋数之差,由于八个分支的结构相同,形成的反螺旋系的秩为1,故u=8-1=7,则由式(5)得到
两个公式的计算结果均为5,在单支不存在局部自由度的情况下(单支结构运动螺旋发生线性相关),动平台自由度为5,即设备安装板沿垂向的扭转自由度被限制。
综上,能够使设备安装板具有六自由度的球铰结构设计合理。
2 仿真分析
2.1 六、八连杆结构水平向抗冲击性能对比
根据前文分析,所设计的八连杆抗冲击隔离器具有横、纵向刚度一致性的优点。同时,相比于六杆结构而言,其杆组布置形式的特殊性减小了隔冲方向间的夹角范围,提高了隔冲杆组利用率,故将通过仿真计算对此结论进行进一步分析。
首先,建立六连杆隔离器的三维模型,如图6所示,并将其导入至ADAMS软件中,设置单位类型为MKS即m、kg、s(米、千克、秒);与八杆结构相同,利用ADAMS建立该虚拟样机的运动副,其中在上、下球座与基座、顶板之间和外部套筒处建立固定副,隔冲杆内部建立移动副,上、下球铰结构建立球副。

图6 六连杆结构Fig.6 Six connecting rod structure
其次,通过准静态压缩试验,获得隔冲杆的静刚度曲线,并将其拟合成样条曲线作为六、八连杆隔离器的刚度参数,刚度曲线如图7所示。
同时,设定其他仿真参数,本次仿真中采用冲击函数法(Impact)进行接触计算,接触类型为实体与实体(Solid-Solid),材料接触刚度为1×108N/m,贡献指数(Force Exponent)为2.2,切入深度为1×10-4m;利用AKISPL函数,将输入载荷拟合为正负双正弦的样条曲线作为水平向的冲击驱动,其正波脉宽6 ms,负波脉宽14.5 ms,正波加速度峰值为120.51g,负波加速度峰值为65.6g。其冲击方向如图8所示,分别沿横向、纵向对六杆隔离器的进行冲击仿真。而由于八杆结构中水平向上的横、纵向结构及刚度一致,故只对其进行横向冲击仿真。

图7 静刚度曲线Fig.7 Static stiffness curve
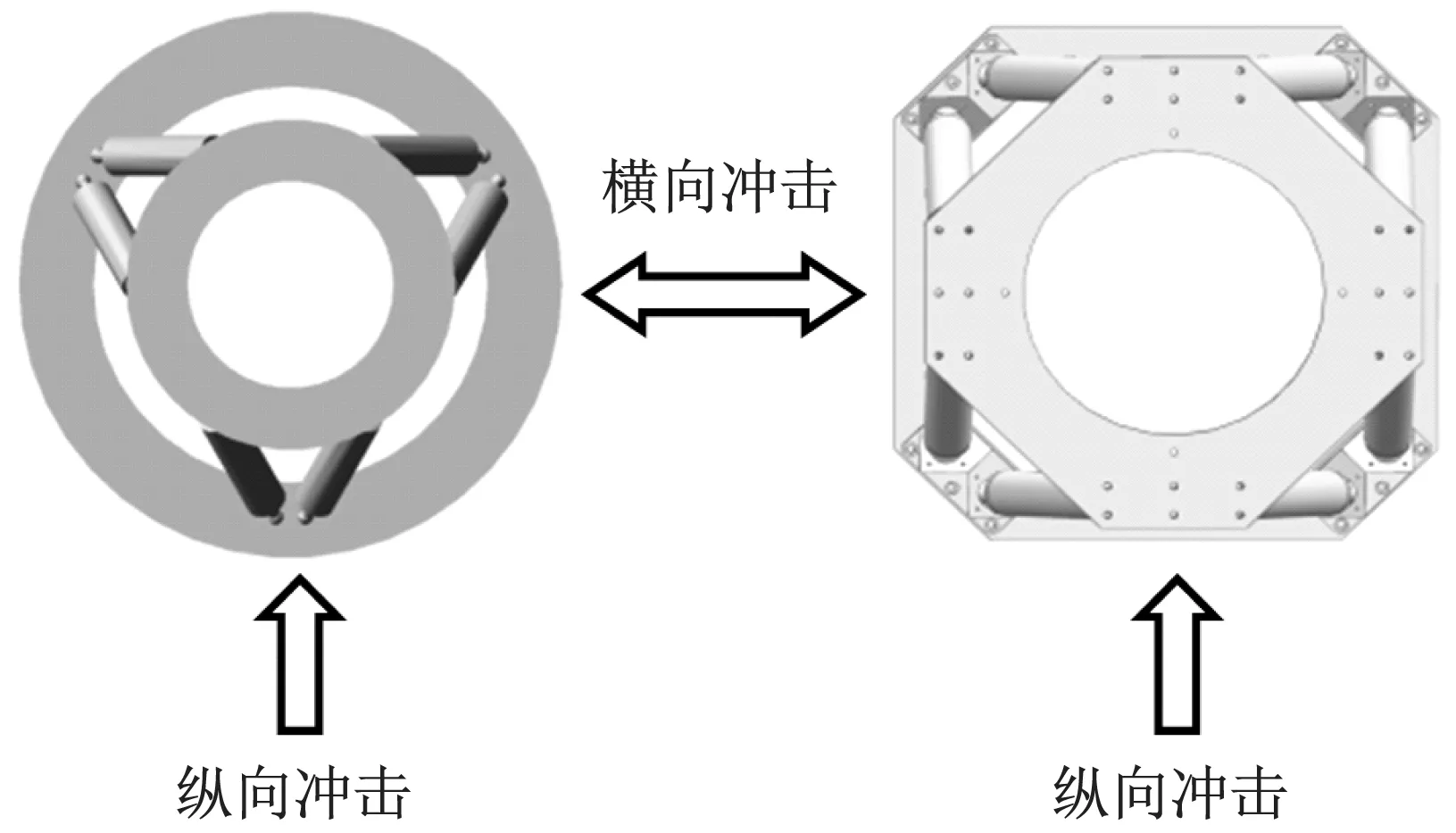
图8 冲击方向Fig.8 Impact direction
最后,对六杆及八杆结构进行仿真计算,设定仿真步数为1 000,时间为0.3 s。
从图9两种结构的水平向加速度响应中得出,六连杆隔离器的纵向冲击加速度响应略小于横向,且响应曲线更平滑。横向的加速度响应曲线存在较多突变的峰点,且该响应结果曲线在0.07~0.17 s间存在非规律性变化,除计算误差外,很有可能是六连杆隔离器隔冲夹角范围大、隔冲杆利用率低导致的响应突变和响应曲线的随机性变化。综合对比八连杆结构,在初始阶段,八杆对加速度的隔离效果好于六杆结构,但两种结构区别不大;在随后的时域曲线中,明显得出八连杆结构的准零特性较为明显,水平向对冲击载荷的隔离效果明显好于六杆结构。

图9 六杆及八杆结构的加速度响应Fig.9 Acceleration response of six and eight rod structure
2.2 冲击载荷与阻尼对隔离器的影响
设备加速度响应和相对位移响应是评价抗冲击性能的两个重要参数,因此,将通过改变阻尼系数,分析不同的阻尼系数对加速度及相对位移响应的影响,以了解阻尼系数与冲击响应幅值的一般规律。
固定隔冲杆的几何参数以及刚度特性,在Design Variable中设定参数C,其值为隔冲杆内部的阻尼系数,将其取值为0.01 N·s/m、0.1 N·s/m、10 N·s/m、40 N·s/m、100 N·s/m,由此得到不同阻尼系数下,八连杆抗冲击隔离器中被隔离设备的加速度以及相对位移响应,如图10、11所示。

图10 不同黏性阻尼下的加速度响应变化Fig.10 The change of acceleration response under different damping
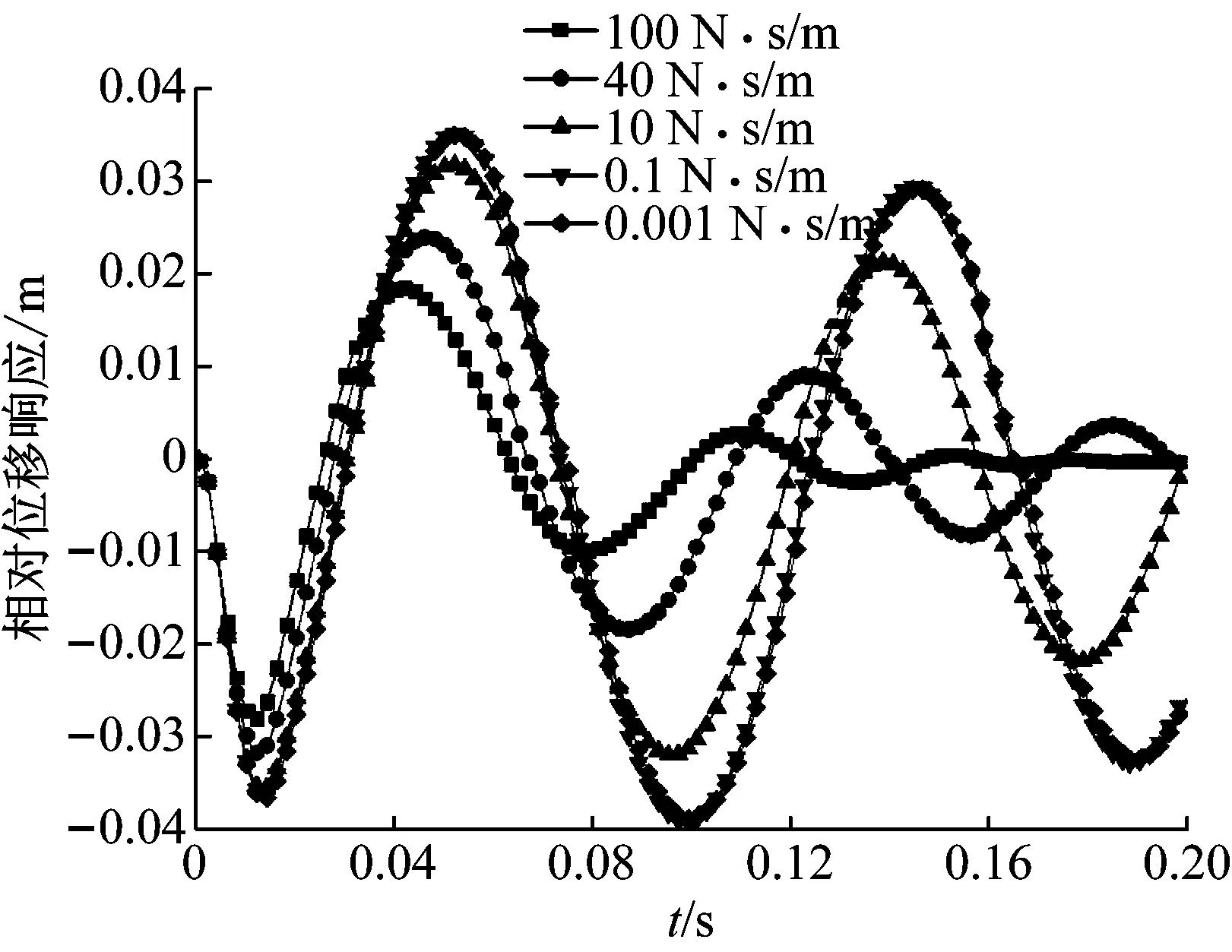
图11 不同黏性阻尼下的相对位移响应变化Fig.11 Change of relative displacement response under different damping
由响应结果可知,阻尼系数对设备加速度及相对位移响应的衰减周期有较大影响,即当阻尼系数增大时,能够使设备响应加速衰减。在响应幅值方面,设备相对位移响应幅值和阻尼系数呈反比关系,但对于加速度响应来说,当黏性阻尼系数变化幅度较小时,改变阻尼大小对设备加速度响应幅值影响并不明显。
为分析所设计的八连杆抗冲击隔离器在不同脉宽下的抗冲击特性,将对隔离器进行多工况下的冲击仿真,将三折线谱转化为正、负双正弦信号作为冲击激励。在谱加速度、谱位移不变的条件下,改变谱速度能够改变双正弦激励的正波脉宽,同时保证正波加速度峰值保持不变,故设定谱速度分别为5 m/s、6.2 m/s、7.4 m/s以及8.6 m/s,对八连杆抗冲击隔离器进行垂向冲击仿真,从而分析不同的冲击脉宽下的隔离器抗冲击性能。
从图12的加速度响应波形上看,改变脉宽对设备的加速度响应衰减周期影响不大。在幅值方面,改变脉宽会使加速度响应幅值变大,但增长幅度较小。由此可得出所设计的八连杆隔离器具有广泛的抗冲击区间,隔冲范围满足抗冲击要求。
图13的位移响应曲线上得出,在正波加速度峰值不变的条件下,随着脉宽变大,位移响应幅值有微量增加,变化并不明显,体现了隔离器稳定的抗冲击性能。

图12 不同谱速度下的加速度响应变化Fig.12 The change of acceleration response at different spectral velocity

图13 不同谱速度下的相对位移响应变化Fig.13 Variation of relative displacement response at different spectral velocities
3 冲击试验及仿真对比
为验证八连杆抗冲击隔离器的隔离率是否满足要求,将根据德国BV043-85的相关规定,通过500 kg双波冲击试验机对隔离器进行冲击,冲击方向为沿垂向及倾斜30°表示的横向。图14、15中,将加速度传感器分别安装置至设备顶面中心和冲击台面上,以此来获得冲击及响应加速度、速度及相对位移,其中垂向冲击加速度幅值为139.31g,横向冲击加速度幅值为110.78g,冲击脉宽约为20 ms。

图14 垂向冲击试验Fig.14 Vertical impact test

图15 横向冲击试验Fig.15 Lateral impact test
同时,将试验获得的冲击数据生成样条曲线,作为仿真中的冲击激励,其余参数设定与前文中一致,通过仿真计算响应结果并与试验数据进行对比,其中图16为冲击仿真示意图。

图16 垂向及横向仿真示意图Fig.16 Schematic diagram of vertical and lateral simulation
通过图17、18的数据显示,试验及仿真结果的加速度响应曲线均呈矩形分布,耗能效率更高,体现了隔离器的准零特性。而在后期的衰减结果中,垂向加速度响应在仿真数据中略大于试验结果,这是由于八杆结构的复杂性,导致其加工存在一定的误差,以及隔冲杆内部弹性元件间剧烈摩擦产生的库伦阻尼加速了衰减过程。
同理,分别在垂向、倾斜横向的安装位置下,逐级施加不同的冲击载荷,对比分析试验及仿真的加速度响应幅值,见表1、2。

图17 垂向加速度响应对比Fig.17 Comparison of vertical acceleration responses
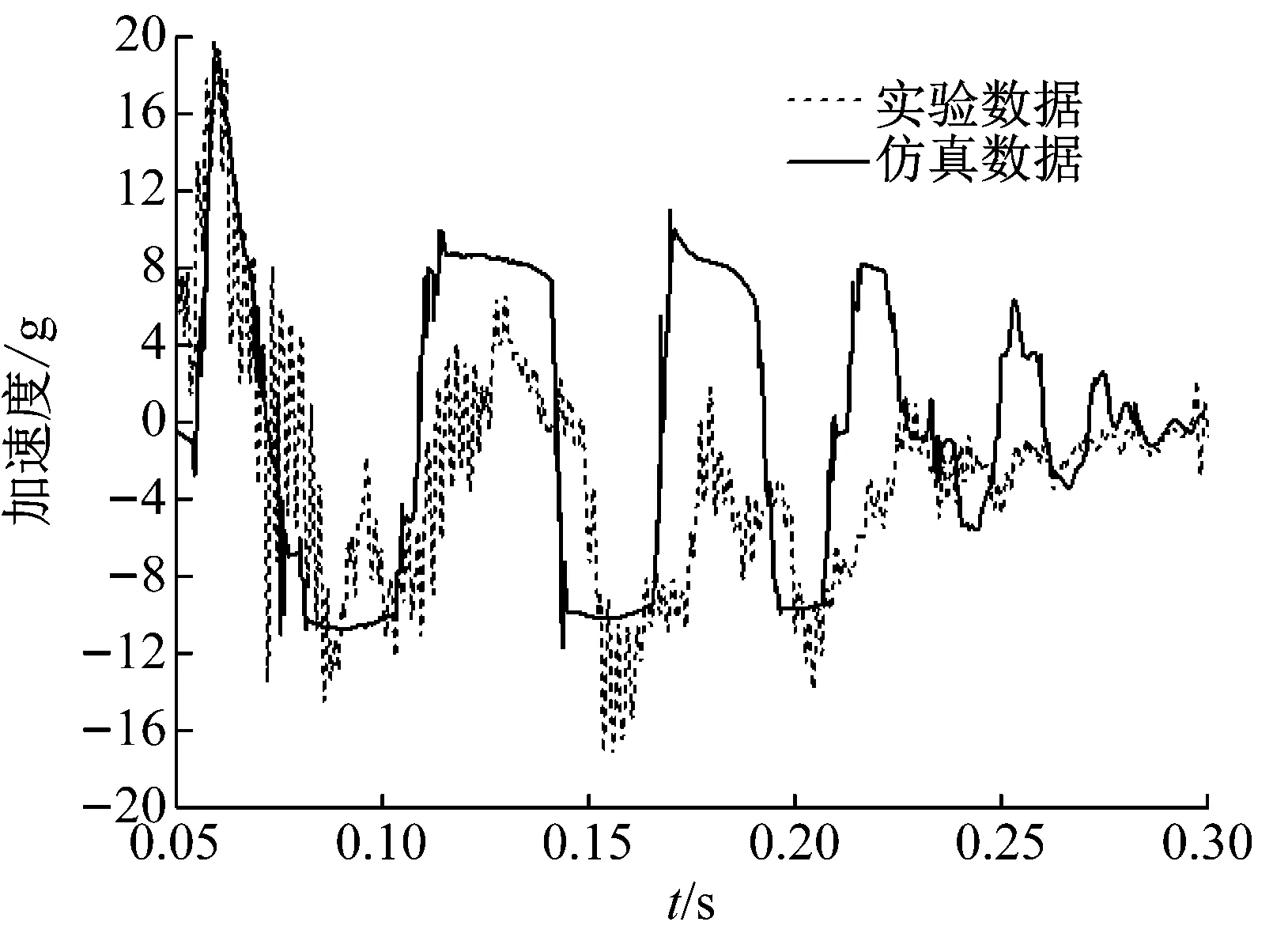
图18 横向加速度响应对比Fig.18 Comparison of lateral acceleration responses

表1 垂向加速度响应对比Tab.1 Comparison of vertical acceleration responses
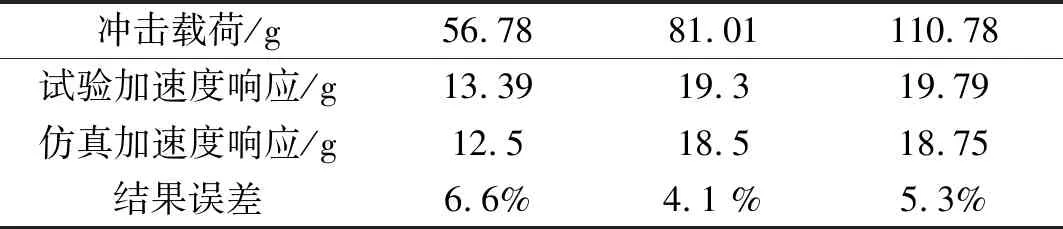
表2 横向加速度响应对比Tab.2 Comparison of lateral acceleration responses
明显得出,仿真及试验的响应幅值误差在5%左右,验证了理论计算的合理性。表中仿真幅值略小于试验幅值,这是由于碟簧在长期放置后产生微小的塑性变形,导致刚度增大,软特性被削弱,使试验结果相对较大。
为验证隔离效果,需计算冲击隔离率,其值越大,表示隔离器的冲击隔离作用越显著。冲击隔离率η计算公式为
(6)
式中:Amax1是激励加速度幅值;Amax2是设备加速度响应幅值。
垂向及横向冲击的隔离率计算结果如表3、4所示。

表3 垂向隔离率Tab.3 Vertical isolation rate

表4 横向隔离率Tab.4 Lateral isolation rate
数据显示,随着冲击载荷的逐渐提高,隔离率显著提升,而较小冲击载荷下,虽然隔离率小于百分之八十,但由于隔冲后产生的加速度响应更小,故不会对设备产生冲击破坏,即该结构的隔离效果满足抗冲击要求。
而在横向冲击载荷为81.01g及110.78g时,其加速度响应结果差别不大,体现了隔离器具有稳定的抗冲击性能。
4 结 论
(1)设计了一种多杆并联的八连杆抗冲击隔离器,具有静态刚度高、体积小、高度低、受惯性力影响小的特性;同时其八杆结构的特殊性使杆组与冲击方向的夹角范围更小,提高了载荷分配的均匀性和杆组利用率。
(2)通过螺旋理论验证了所设计的八连杆抗冲击隔离器具有6个自由度,结构合理。
(3)通过仿真对比分析了六、八连杆隔离器的水平向抗冲击能力,得出八连杆抗冲击隔离器水平向加速度响应更小,响应结果更稳定,即抗冲击性能更好。
(4)利用仿真分析了阻尼及冲击载荷对隔离器的影响,得出结论:
在时域上,改变阻尼系数能够缩短响应的衰减周期。在响应幅值方面,阻尼系数对相对位移响应幅值影响较大,但当黏性阻尼系数变化幅度较小时,改变阻尼系数大小对设备加速度响应幅值影响不大。
当增加冲击脉宽时,设备的响应周期基本不发生变化,虽然加速度响应幅值有所增大,但增长幅度非常小,说明八连杆抗冲击隔离器的隔冲范围广。同时,位移响应曲线基本没有发生变化,也说明了该结构具有稳定的抗冲击性能。
(5)根据冲击试验验证了理论结果的正确性,并通过计算垂向及横向的隔离率,得到随冲击载荷的逐渐提高,隔离率有显著提升,隔离器效果满足抗冲击要求;在分析横向冲击结果时发现,当冲击载荷较大时,加速度响应结果差别不大,说明八连杆隔离器具有稳定的抗冲击性能。
综上,所设计的八连杆抗冲击隔离器结构合理,并具有理想的抗冲击特性。进一步得出,机械设计理论与冲击领域的深度结合,能够为隔离装置的优化设计提供理论依据。

