曲面隔震结构的动力模型与振动台试验研究
田 坤,刘文光,孙 实,何文福
(上海大学 土木工程系,上海 200444)
地震灾害会造成巨大的经济损失和人员伤亡,因此,如何减小地震造成的损失是土木工程学科研究的重点。基础隔震技术可以有效减小隔震结构的地震响应,不仅可以保护建筑主体结构的安全,也可以保护建筑物的附属构件不受破坏。基础隔震技术从20世纪70年代开始在实际工程中应用,经过将近50年的发展,在橡胶支座试验和理论分析等方面都取得了丰富的成果。Gent等[1-3]对橡胶块的力学性能进行了系统的研究。Takayama等[4]对铅芯橡胶支座的极限变形和耗能能力进行了试验研究。Abe等[5-6]对橡胶支座在多向加载情况下的性能进行了试验和理论研究。张子翔等[7]提出一种用于描述支座在水平方向加载力学性能的宏观滞回模型。
随着隔震技术的发展和隔震建筑的兴建,国内外学者对隔震结构在理论研究、试验和应用方面已经展开研究。吕西林等[8]完成了高宽比为2.2的组合隔震结构振动台试验。吴香香等[9]给出了基础摩擦隔震的高宽比限值及竖向地震的影响。Kaplan等[10]对40层钢框架高层隔震结构进行了优化设计研究。Ariga等[11]研究了基础附加摩擦隔震系统的10层高层建筑结构在长周期地震作用下的共振响应。Ikeda等[12-15]采用空间振动地震响应分析程序对高层隔震结构的上部结构地震响应进行研究,并评价了支座的提离现象;他们也研究了水平和竖向地震作用对高层隔震结构支座拉伸的影响,并考察了实际强震下大高宽比隔震结构拉伸反应。何文福等[16]对5层钢框架隔震结构模型进行了振动台试验,研究不同高宽比隔震模型在多维地震作用下的动力响应。刘文光等[17]基于基底剪力和能量等效原则提出一种可快速计算高层隔震结构地震响应的单纯质点法。刘阳等[18]对复杂博物馆结构1/30缩尺模型进行了振动台试验。朱宏平等[19]在考虑隔震支座水平竖向力学性能耦合作用的基础上对隔震结构在近断层水平-竖向地震联合作用下的动力响应进行了研究。
当水平隔震结构遭受强地震作用时,隔震层会发生较大的水平位移,对橡胶隔震支座的竖向承载力产生影响,当隔震层水平变形超过隔震沟预留宽度时,建筑结构会与挡土墙发生碰撞,影响结构整体稳定性。因此,为了控制隔震结构的隔震层水平位移,增加上部结构稳定性,本文提出了曲面隔震结构这一新型隔震结构体系,在小幅增加上部结构加速度响应的前提下控制隔震层位移。根据整体结构的支座平面布置及隔震层曲率半径,对曲面隔震结构隔震支座的竖向标高及倾角进行精细化设计,然后对隔震支座承台进行调整,确保隔震层进行曲面运动时所有隔震支座变形协调。根据上部结构柱端反力与相应隔震支座的倾斜角度对支座实际受力状态进行计算,根据隔震支座实际受力情况对隔震层支座进行统一设计。倾斜隔震支座竖向分量的力承担上部结构重量,由于隔震层整体是一个对称的球面,隔震支座均朝向隔震层曲率中心倾斜布置,因此隔震层中支座水平方向分量的力相互平衡,对整体隔震效果不会产生不利影响。当受到地震作用时,上部结构绕隔震层曲面的曲率中心转动,隔震层运动轨迹是一个球面(图1)。然后针对曲面隔震结构体系建立了隔震支座倾斜布置的简化单质点分析模型,对其加速度传递系数和位移传递系数进行了理论分析。最后制作了曲面隔震结构模型,与平面隔震结构模型和非隔震结构模型分别进行了振动台试验,对比分析了曲面隔震结构模型与平面隔震结构模型及非隔震结构模型的地震响应。
1 简化模型理论分析
图2为曲面隔震结构双排支座简化分析模型,其中x为曲面隔震结构隔震层水平位移,x1为上部结构质心处水平位移,xg为地面的地震位移,R为曲面隔震结构隔震层的曲率半径,H为上部结构质心高度,2B为结构宽度,Kh1为单排橡胶隔震支座水平刚度,Kv1为单排橡胶隔震支座竖向刚度。
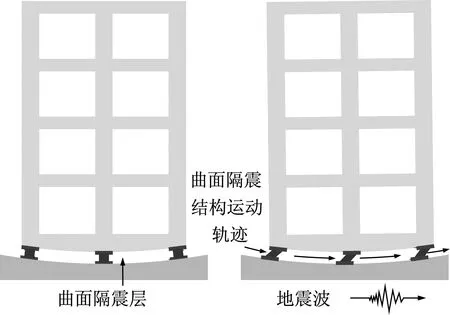
图1 曲面隔震结构概念图Fig.1 Schematic of curved surface isolated structure
曲面隔震结构径高比定义为隔震层曲率半径与结构高度的比值,假设结构重心位于结构形心,结构总高度为2H,径高比可写为
(1)
曲面隔震结构由于支座倾斜布置,因此在图2所示曲面隔震结构简化分析模型当中,橡胶隔震支座自身的水平刚度和竖向刚度在整体模型水平方向分解之后的等效水平刚度Ke可写为
Ke=2Kh1·cosθ+2Kv1·sinθ
(2)
其中θ为支座倾斜角度,简化分析模型中两排支座倾斜角度相同,因此式(2)可写为
Ke=Kh·cosθ+Kv·sinθ
(3)
其中Kh为隔震层隔震支座水平刚度之和,Kv为隔震层隔震支座竖向刚度之和。
根据几何关系上式可写为
(4)
曲面隔震结构水平方向动力学方程为
(5)
模型上部结构质心处水平位移和隔震层水平位移之间存在如下几何关系
(6)
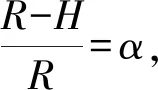
(7)
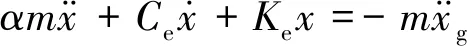
(8)
定义曲面隔震结构体系的水平方向固有频率ωn及阻尼比ξ

(a)曲面隔震结构力学模型
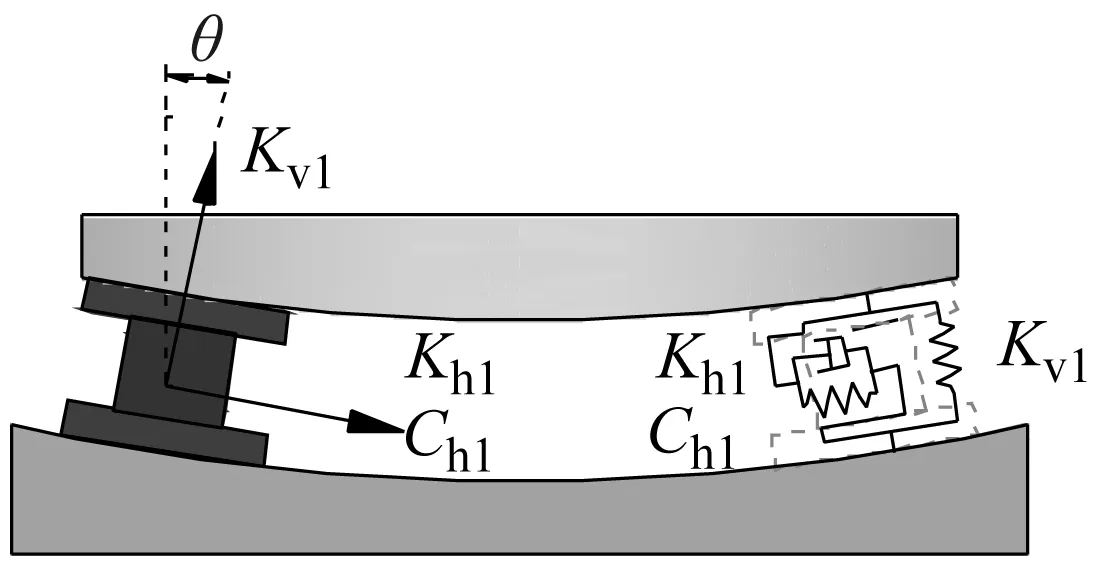
(b)曲面隔震结构隔震层力学模型图
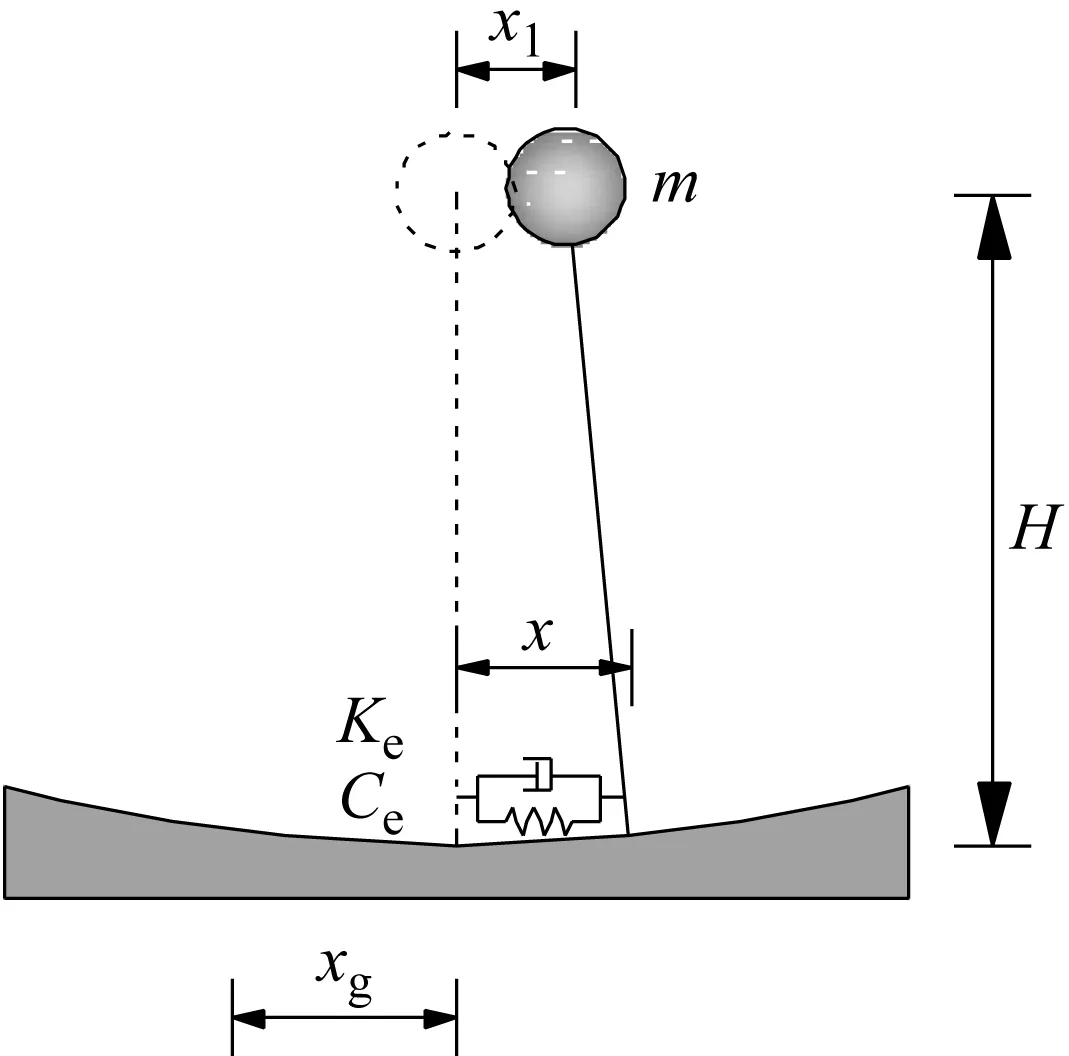
(c)曲面隔震结构简化分析模型
(9)
(10)
式中:ωnh代表隔震层总体水平刚度对应固有频率,ωnv代表隔震层总体竖向刚度对应固有频率。
曲面隔震结构水平方向动力学方程式(7)和式(8)分别可写为
(11)
(12)

(13)
由此可得曲面隔震结构加速度传递系数
(14)
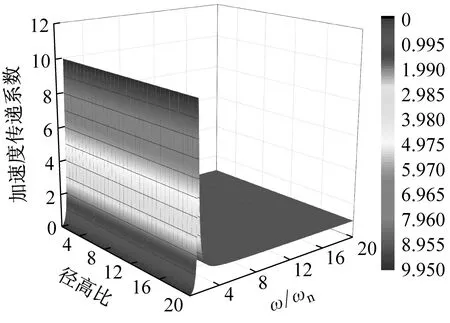
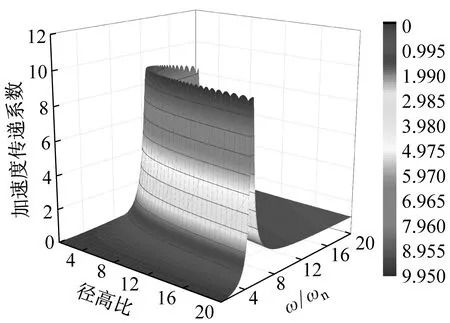
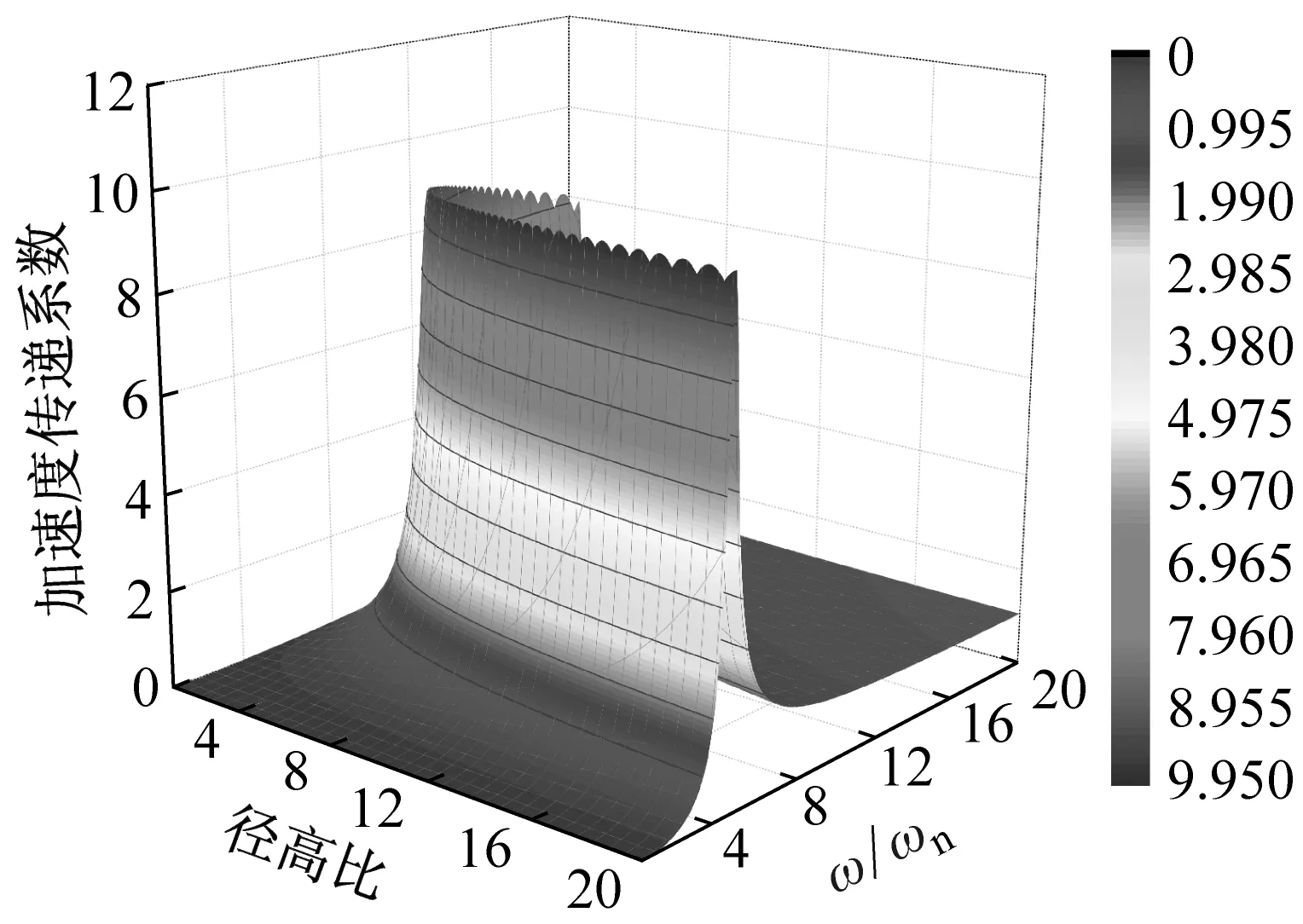
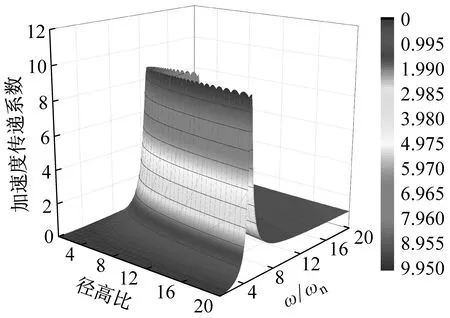
根据式(14)画出曲面隔震结构加速度传递系数与结构径高比γ和外部激励频率与结构自振频率比值ω/ωn之间关系的三维图。平面隔震结构加速度传递系数三维图参照结构动力学[20]公式进行绘制。图3(a)为平面隔震结构加速度传递系数三维图,图3(b)、(c)、(d)分别为结构高宽比为3、4、5时曲面隔震结构加速度传递系数三维图。
从加速度传递系数三维图中可以看出,平面隔震结构加速度传递系数只有一个峰值,但是曲面隔震结构加速度传递系数有多个峰值,并且随着结构径高比的变化,加速度传递系数峰值出现位置也发生变化,这是由于曲面隔震结构隔震层曲率与外部激励产生共振引起的,进行曲面隔震结构设计时应避开这个径高比范围。曲面隔震结构加速度传递系数大于平面隔震结构,随着结构径高比的增大,曲面隔震结构加速度传递系数趋向于平面隔震结构。
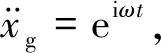

(15)
由此可得曲面隔震结构位移传递系数
(16)
参照式(16)画出曲面隔震结构位移传递系数与结构径高比γ和外部激励频率与结构自振频率比值ω/ωn之间关系的三维图。平面隔震结构位移传递系数三维图参照结构动力学[20]公式进行绘制。图4(a)为平面隔震结构位移传递系数三维图,图4(b)、(c)、(d)分别为结构高宽比为3、4、5时曲面隔震结构位移传递系数三维图。
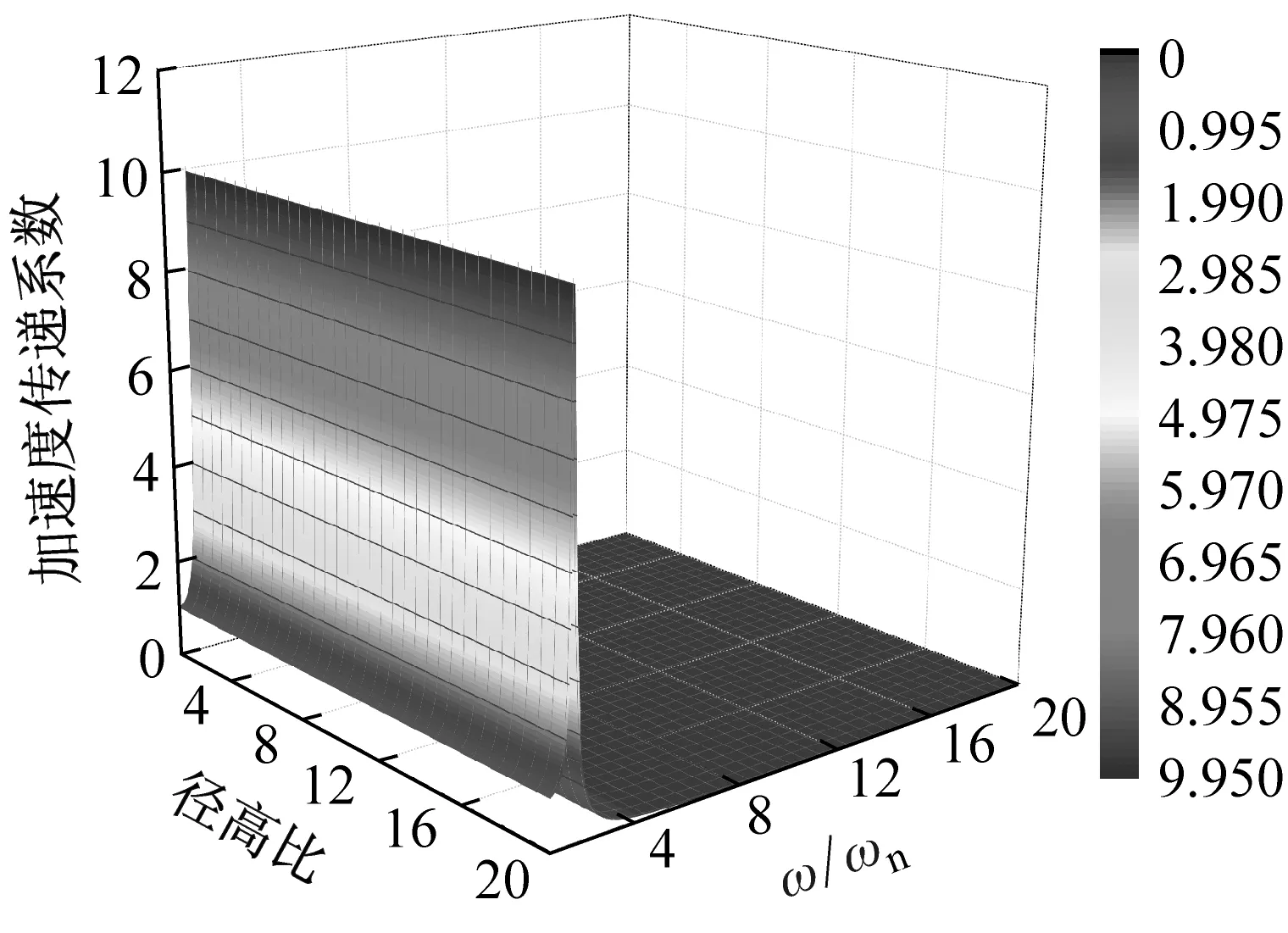
(a)平面隔震结构
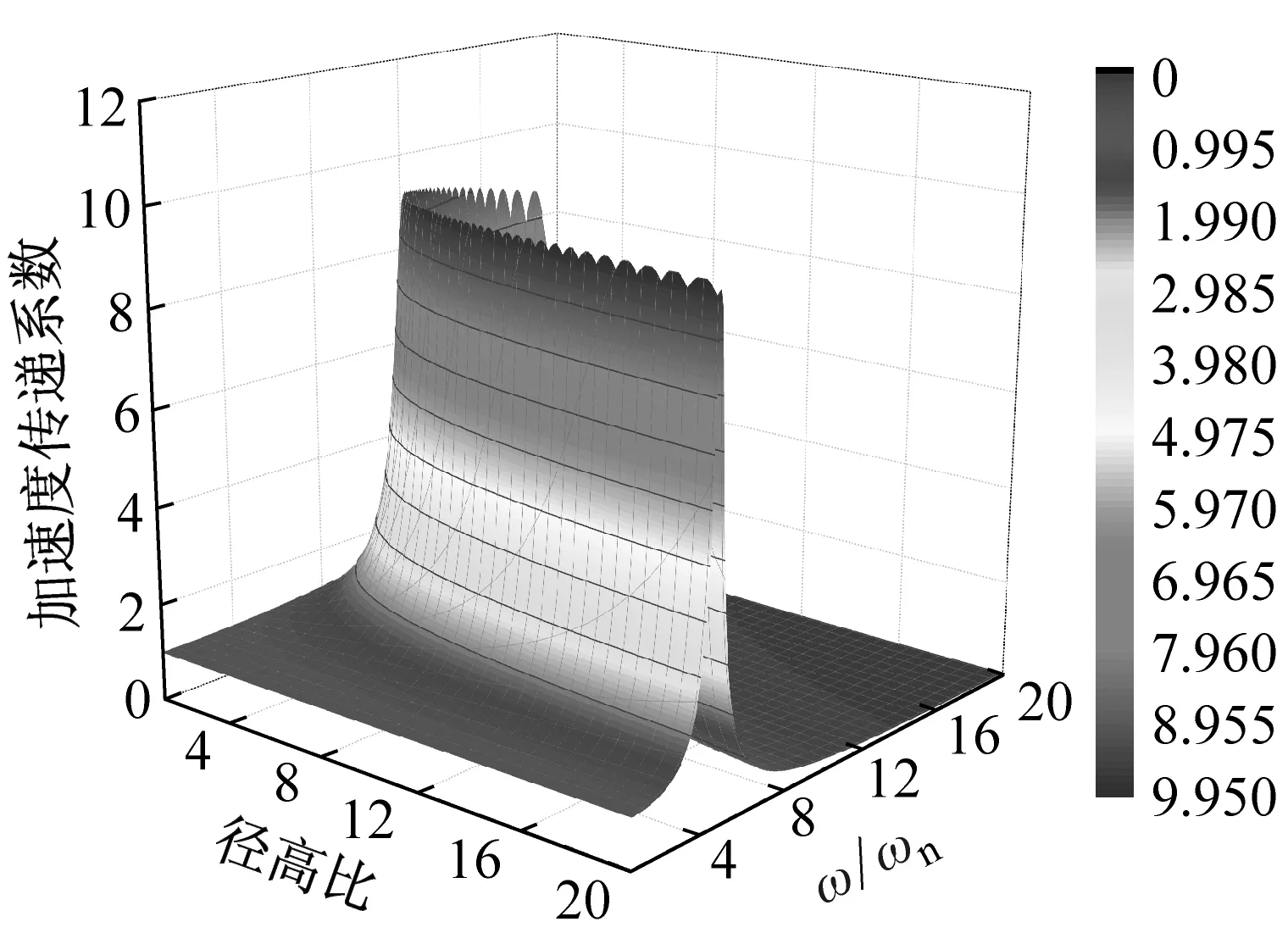
(b)曲面隔震结构(高宽比3)

(c)曲面隔震结构(高宽比4)

(d)曲面隔震结构(高宽比5)
(a)平面隔震结构
(b)曲面隔震结构(高宽比3)
(c)曲面隔震结构(高宽比4)
(d)曲面隔震结构(高宽比5)
位移传递系数三维图表现出与加速度传递系数三维图相类似的规律,但是在结构径高比较小时曲面隔震结构位移传递系数小于平面隔震结构,随着结构径高比的增大,曲面隔震结构因产生共振使得位移传递系数增大并超过平面隔震结构,随着径高比的进一步增大,曲面隔震结构位移传递系数趋向于平面隔震结构。
2 试验概况
2.1 试验模型设计
试验上部结构模型采用的是5层钢结构模型,梁柱节点与梁梁节点均为焊接,模型各层层高均为980 mm,隔震层高度为380 mm,模型总高度为5 280 mm。模型X方向宽度为810 mm,高宽比为6;模型Y方向宽度为1 620 mm,高宽比为3。试验模型各构件均采用Q345钢材,各杆件截面尺寸如表1所示,图5和图6分别为试验模型柱和底梁构件尺寸详图。在模型1层和模型顶部各布置1 t配重,模型2~5层各布置2 t配重,配重总计10 t。试验模型相似关系如表2所示。根据曲面隔震结构加速度传递系数与位移传递系数的理论分析,在减小结构位移反应的径高比范围内选取此次振动台试验曲面隔震结构模型径高比,综合考虑结构加速度响应、位移响应和倾斜连接件加工等因素,此次振动台试验曲面隔震结构模型径高比γ定为2.6。根据曲面隔震结构隔震层设计方法,将隔震支座均朝向隔震层曲率中心倾斜布置,曲面隔震结构模型照片及立面尺寸如图7所示,曲面隔震层具体构造形式如图8所示。

表1 试验模型杆件截面信息Tab.1 Member sections of model structure

(a) 试验模型柱构件尺寸详图(侧视图)(b) 试验模型柱构件尺寸详图(俯视图)(c) 试验模型柱构件尺寸详图(截面图)
试验选取LRB100支座,支座直径100 mm,高度70 mm,橡胶总厚度20 mm。铅芯直径13 mm,支座屈服力1.43 kN,隔震层屈重比4.9%。隔震层高度380 mm,其中支座高度70 mm、三向力传感器高度140 mm和倾斜连接构件及过渡板总高度170 mm。为防止上部结构倾覆,在模型两侧分别安装防倾覆装置,防倾覆装置主要由底部防倒塌支撑钢墩和上部挡梁构成。非隔震结构模型是将上部钢框架通过螺栓固定于振动台台面。非隔震结构周期为0.31 s,平面隔震结构通过理论计算得到隔震周期为0.87 s,曲面隔震结构通过理论计算得到隔震周期为0.71 s。为方便描述,后文图中将曲面隔震结构(Curve Surface Isolated Structure)、平面隔震结构(Normal Isolated Structure)和非隔震结构(Non-Isolated Structure)分别简写为CS-ISO、NOR-ISO和NON-ISO。
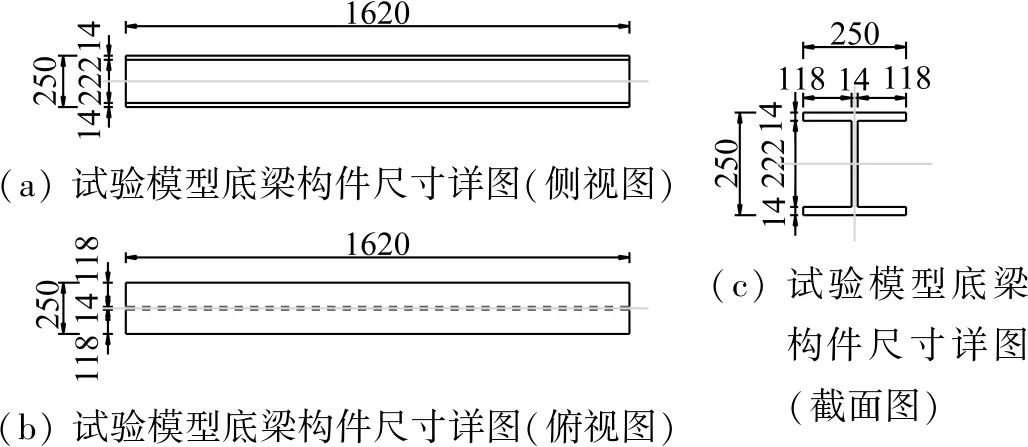
(a) 试验模型底梁构件尺寸详图(侧视图)(b) 试验模型底梁构件尺寸详图(俯视图)(c) 试验模型底梁构件尺寸详图(截面图)
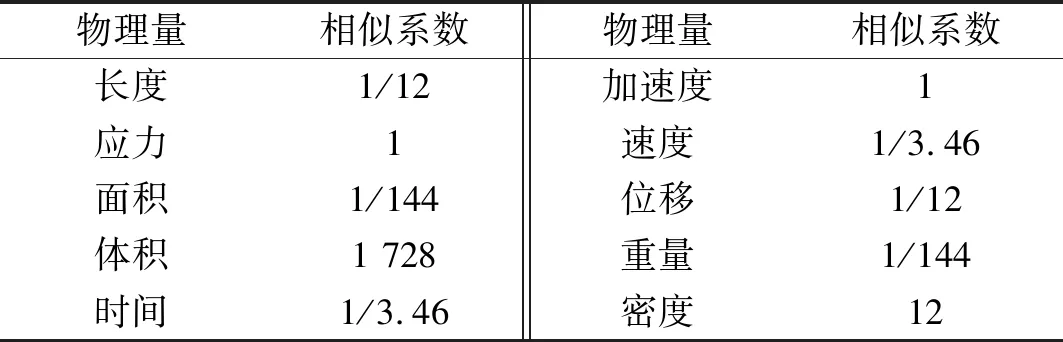
表2 试验模型主要相似系数Tab.2 Similitude factors of model structure

图7 曲面隔震结构试验模型及立面尺寸示意图(mm)Fig.7 Elevations of curved surface isolated structure model(mm)

图8 曲面隔震结构试验模型隔震层构造形式详图Fig.8 Detail of isolation layer for curved surface isolated structure
为测量隔震层及上部结构的位移,分别在隔震层和上部结构的第1层、第3层和第5层顶部布置拉线式位移传感器。为测量上部结构的加速度响应,在上部结构各层顶部布置三向加速度传感器。为测量橡胶隔震支座的受力状况,在橡胶支座底部安装三向力传感器。
2.2 地震波选取及试验工况设计
此次试验所选地震波为El Centro波和Taft波,强震记录来源于太平洋地震工程研究中心地面运动数据库,地震波信息详见表3。

表3 试验选用原始地震波参数Tab.3 Information of original seismic waves
地震波按照时间相似系数压缩后按框架XYZ三方向输入,实际加载工况见表4。此次试验中分别对曲面隔震结构、平面隔震结构和非隔震结构三种结构模型进行了地震模拟振动台试验,对比分析这三种结构的地震响应。出于安全性考虑,非隔震结构三向加载试验只进行了加速度峰值为0.15g试验工况。
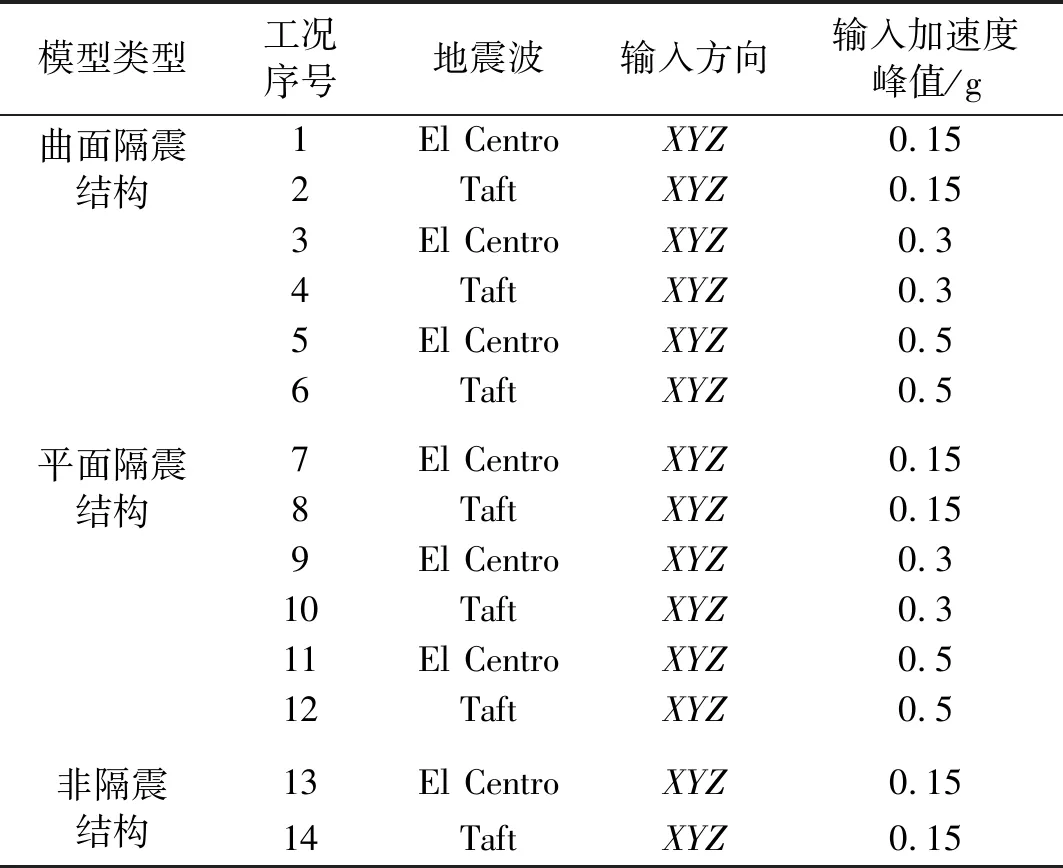
表4 试验工况Tab.4 Test cases
3 试验结果分析
3.1 隔震层响应
隔震结构模型振动台试验中,隔震层的地震响应是关注的重点。图9和图10分别为三向加载El Centro地震波和Taft 地震波不同加速度峰值工况下曲面隔震结构和平面隔震结构支座滞回曲线对比图。
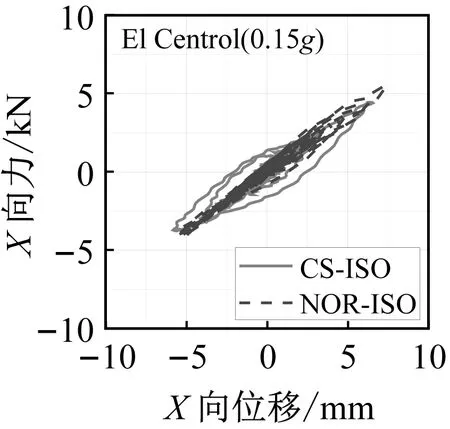
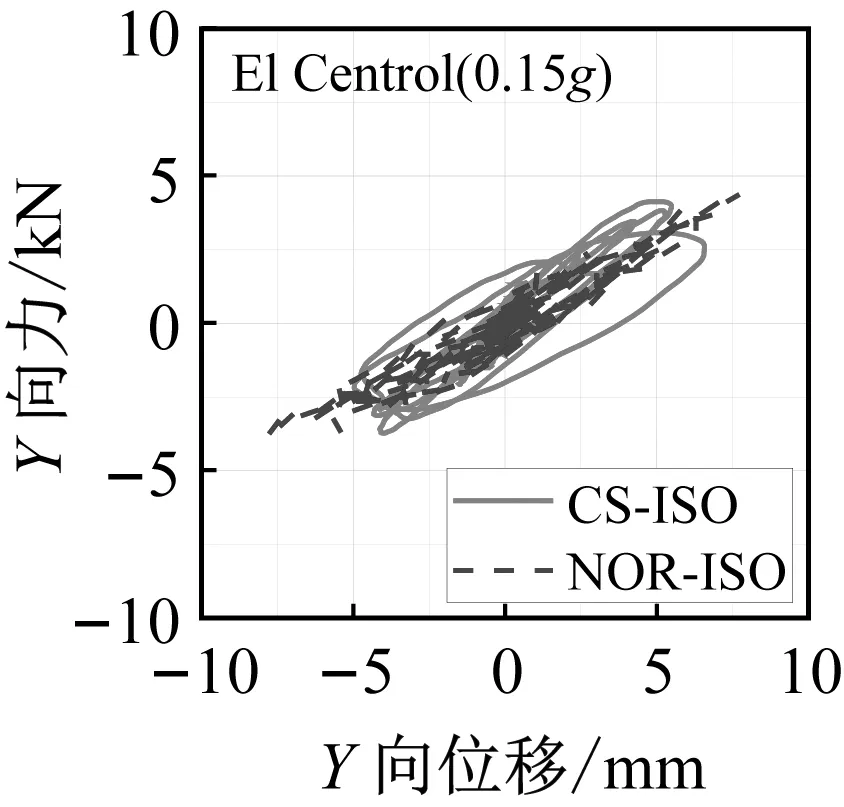
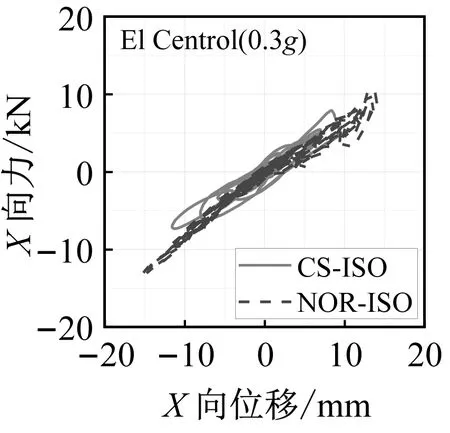

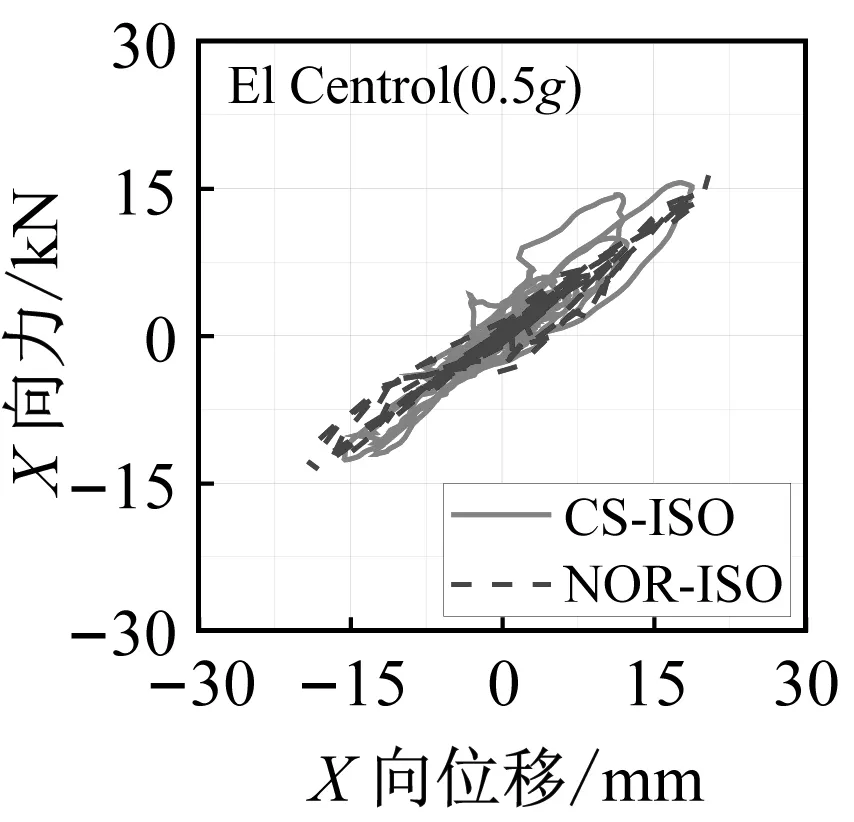
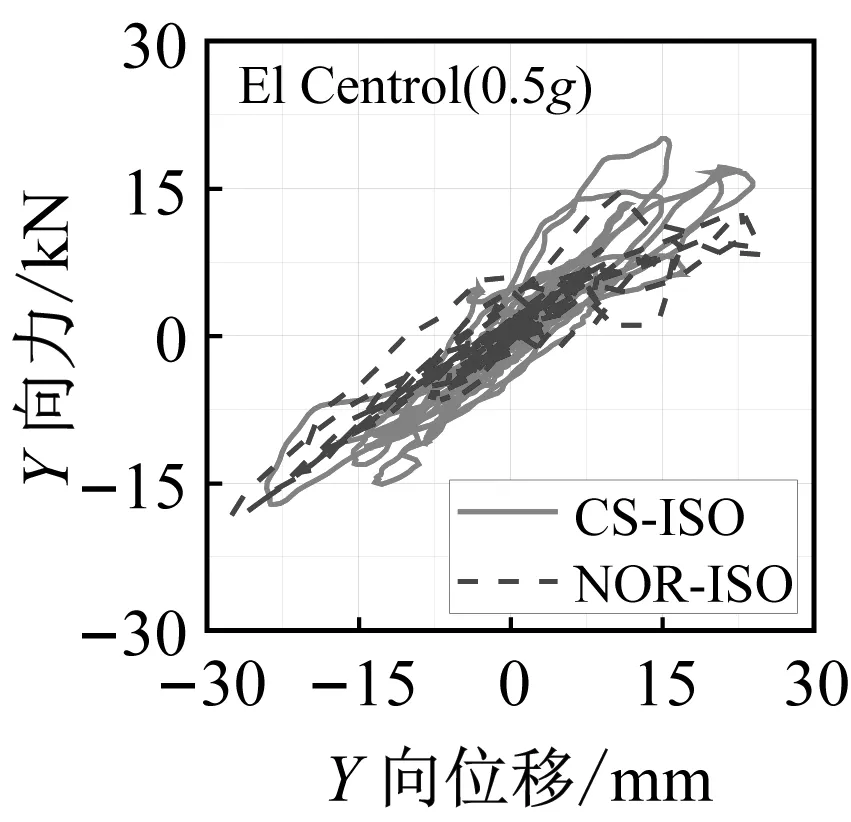
图9 三向加载El Centro地震波工况支座滞回曲线Fig.9 Hysteretic curves of the bearings under El Centro ground motion
从隔震支座的滞回曲线中可以看出,曲面隔震结构模型支座的滞回曲线相对于平面隔震结构来说更加饱满,并且隔震层位移也相应减小。这是由于曲面隔震支座倾斜布置,支座自身的竖向刚度在水平方向产生额外分量造成的。
图11为Taft地震波不同加载加速度峰值工况下隔震层位移时程对比,图12为隔震层位移峰值对比图,图中减小率表示的是曲面隔震结构模型隔震层位移峰值相对于平面隔震结构的减小程度。
三向加载El Centro地震波工况下,隔震层X方向和Y方向位移峰值减小均值分别为15.2%和14.6%;三向加载Taft地震波工况下,隔震层X方向和Y方向位移峰值减小均值分别为32.2%和11.2%。从隔震层位移时程对比中可以看出,曲面隔震结构不但可以有效减小位移峰值,在除峰值外的其他时程区间位移减小率更加明显。由于曲面隔震结构的曲面运动特性及上部结构重力作用,曲面隔震结构隔震层位移衰减速度快于平面隔震结构,有助于结构快速恢复稳定。
3.2 上部结构响应
图13和图14分别为三向加载El Centro地震波和Taft地震波不同加速度峰值工况下曲面隔震结构和平面隔震结构上部结构各层加速度峰值图。
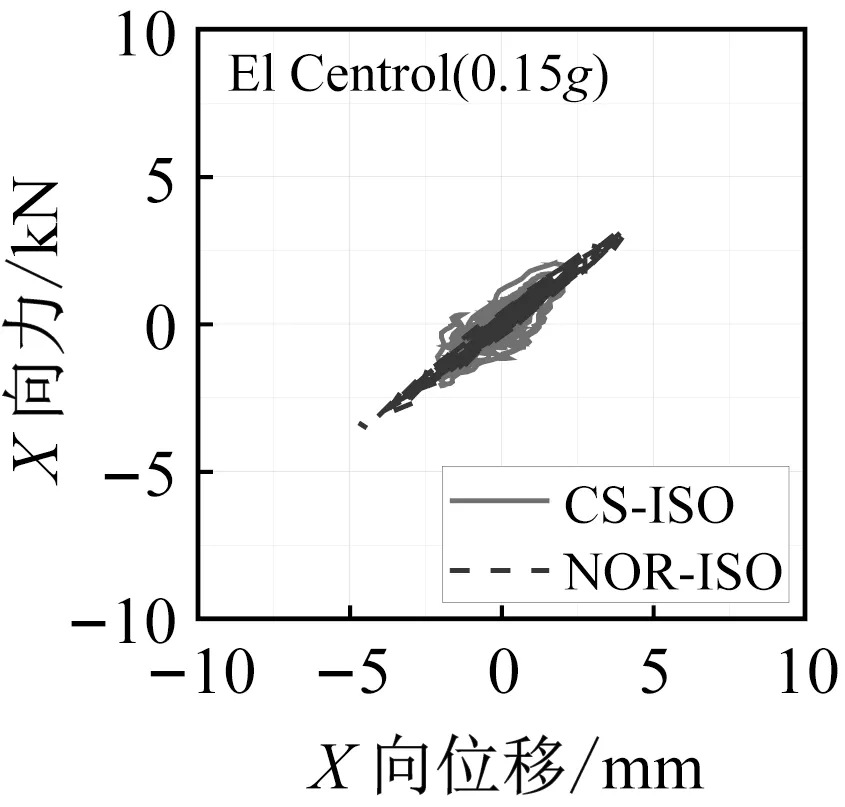
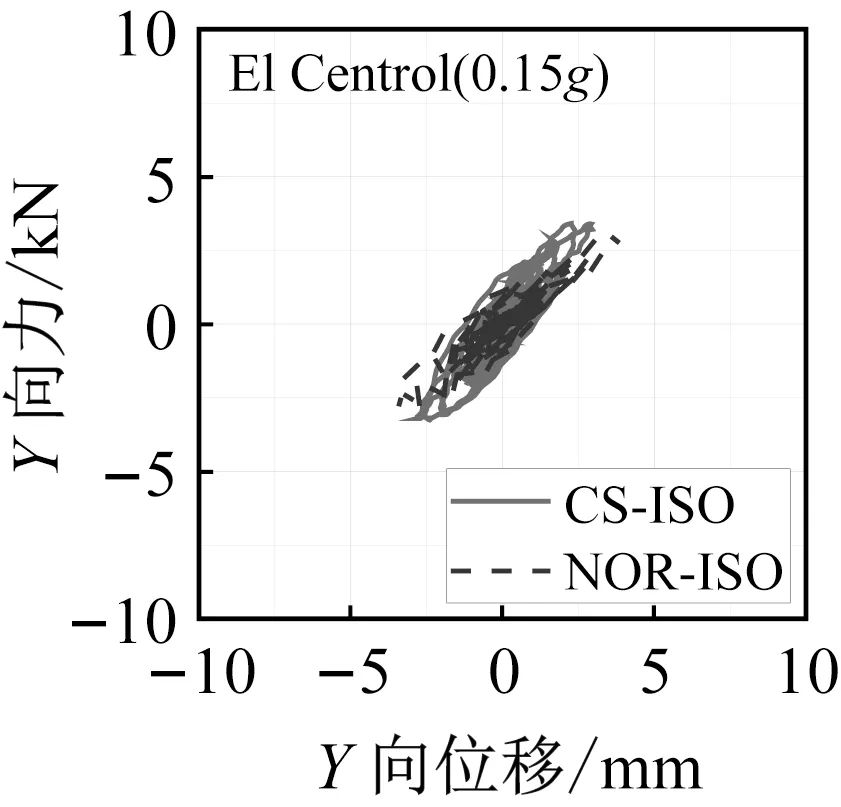



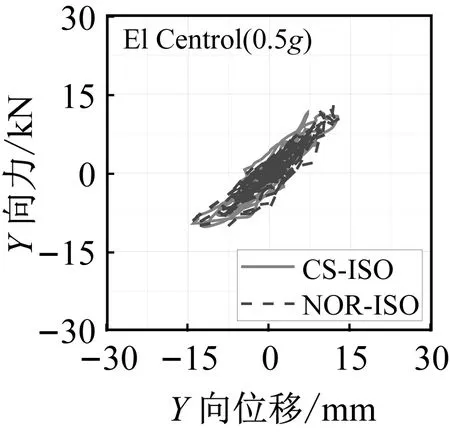
图10 三向加载Taft地震波工况支座滞回曲线Fig.10 Hysteretic curves of the bearings under Taft ground motion
从上部结构加速度峰值图中可以看出,曲面隔震结构加速度响应较平面隔震结构有所放大,但是相对于非隔震结构加速度响应减小程度更加显著,曲面隔震结构的隔震效果良好。
图15和图16分别为三向加载El Centro地震波和Taft地震波不同加速度峰值工况下曲面隔震结构和平面隔震结构层间变形图。图17和图18分别为三向加载El Centro地震波和Taft地震波不同加速度峰值工况下曲面隔震结构和平面隔震结构各层水平位移峰值图。
从上部结构层间变形图中可以看出,由于曲面隔震结构加速度响应放大的原因,造成上部结构层间变形的增大,但是隔震层位移得到有效控制,隔震层位移控制效果相对于上部结构层间位移增大程度更加明显。
从上部结构各层水平位移峰值图中可以看出,平面隔震结构模型在0.15g加速度峰值输入工况下,上部结构各层位移峰值差别很小,上部结构以平动为主,随着输入加速度峰值的增大,上部结构摇摆运动逐渐增大,各层水平位移峰值差距逐渐增大,结构顶部水平位移峰值大于结构底部;曲面隔震结构模型在0.15g加速度峰值输入工况下,上部结构各层水平位移峰值X方向差别不大,但是在Y方向,结构顶部位移峰值小于结构底部,上部结构呈现出绕隔震层曲率中心转动的运动特性,随着输入加速度峰值的增大,这种运动趋势更加明显。综合考虑结构层间变形和结构各层水平位移峰值,平面隔震结构层间变形小于曲面隔震结构,各层位移峰值大于曲面隔震结构并呈现出顶部外甩的运动趋势,可以看出平面隔震结构的倾覆摇摆运动较曲面隔震结构更加明显。曲面隔震结构模型整体位移均小于平面隔震结构,结构在地震作用下的稳定性优于平面隔震结构。
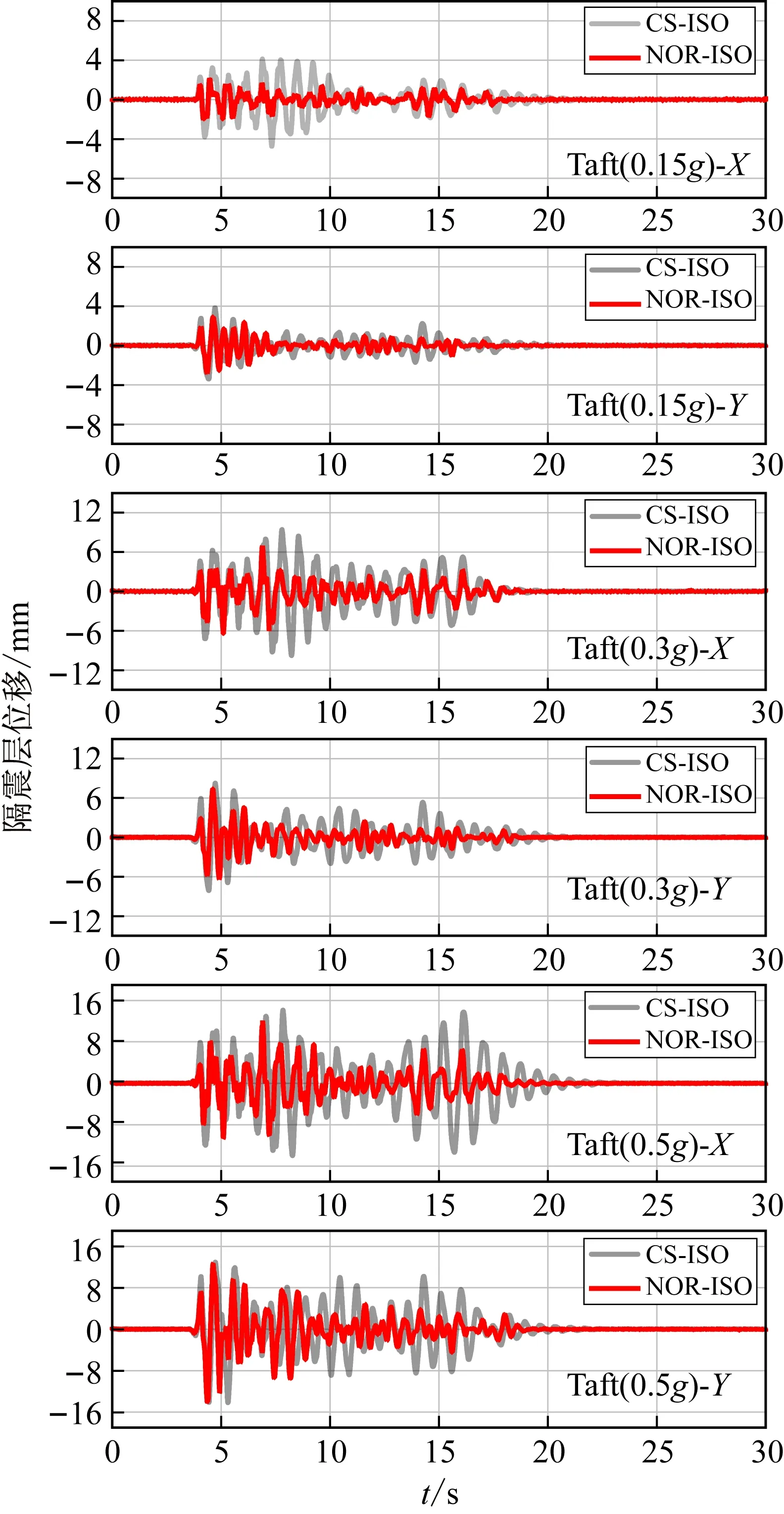
图11 Taft地震波加载工况隔震支座位移时程Fig.11 Displacement time history curves of the bearings under Taft ground motion
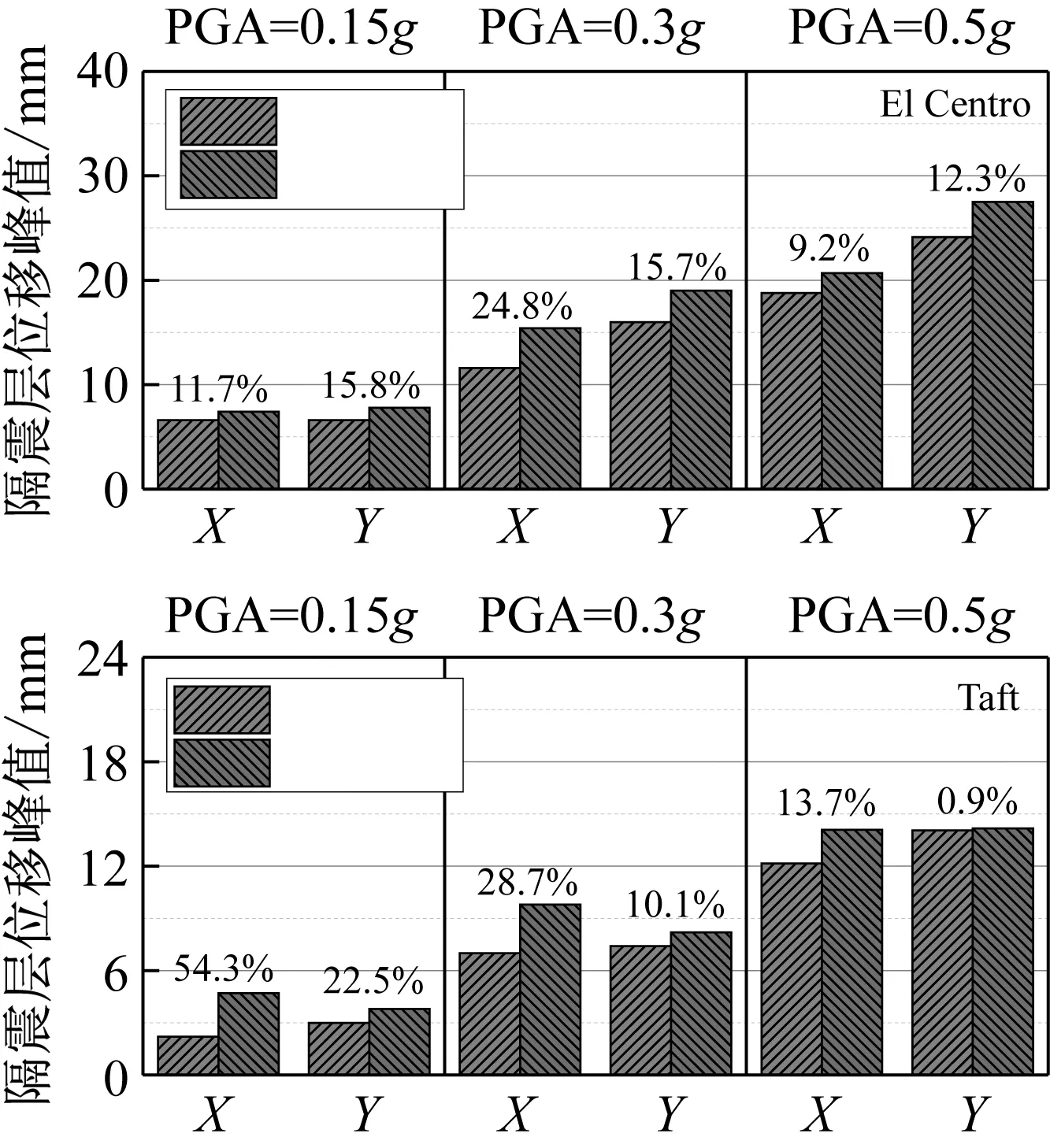
图12 隔震层位移最大值对比详图Fig.12 Comparison of maximum displacement of isolation layer for CS-ISO and NOR-ISO
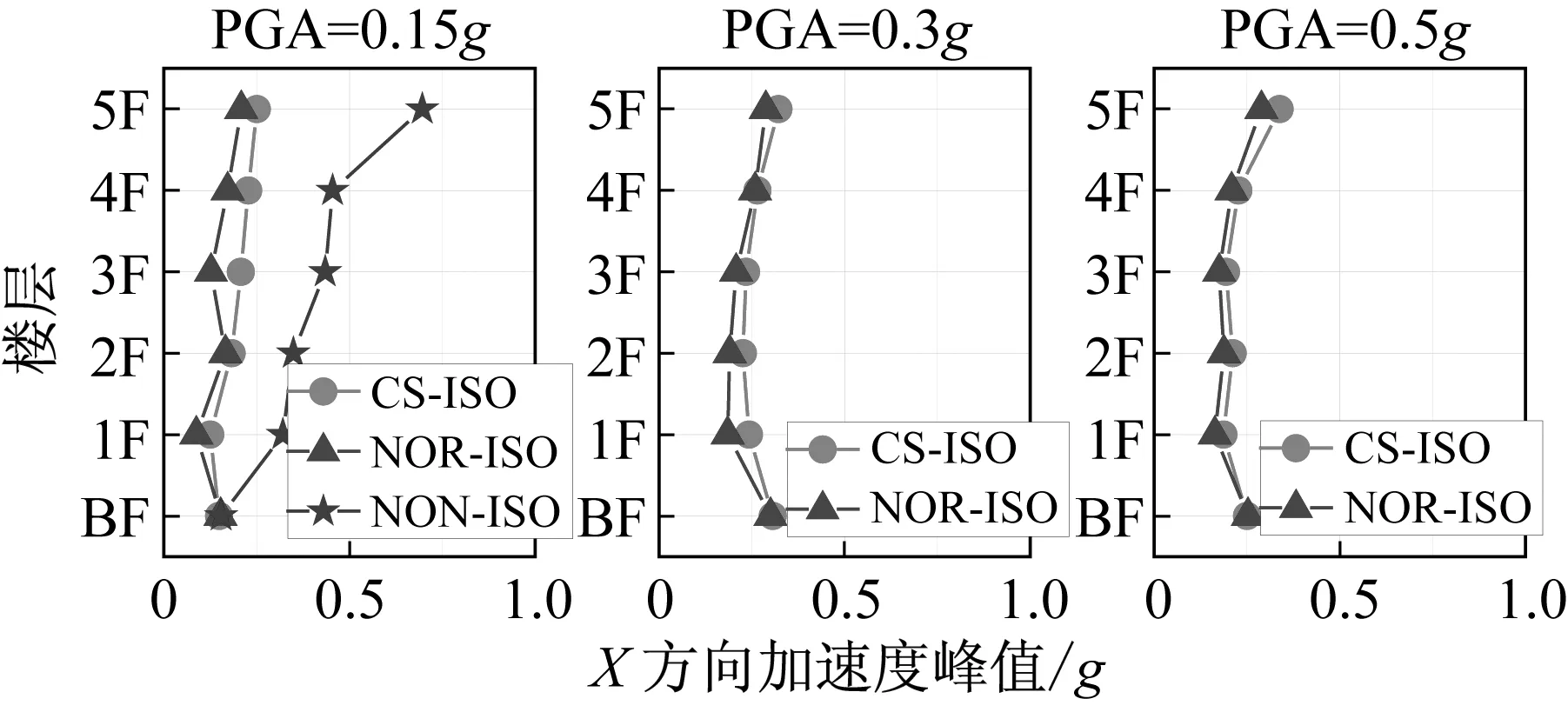
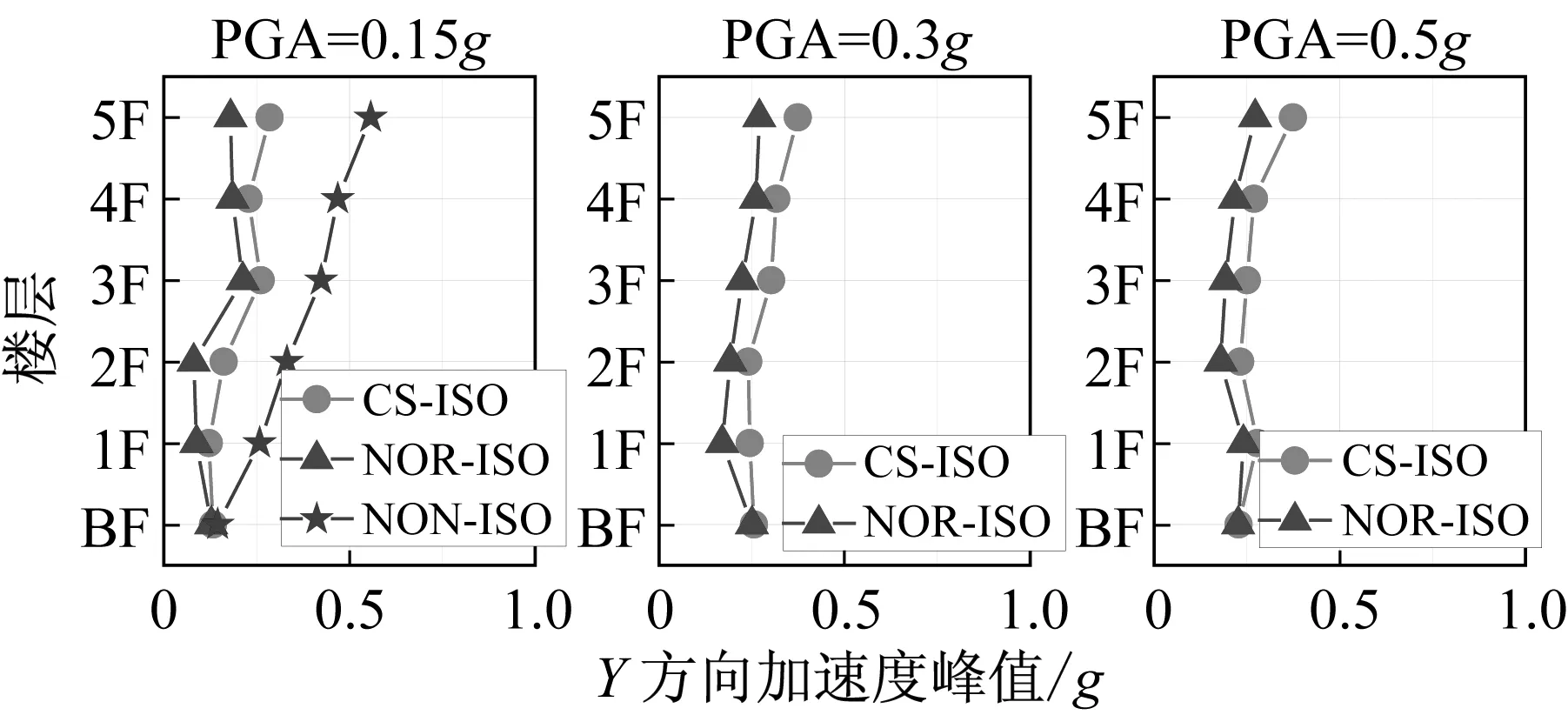
图13 三向加载El Centro地震波工况各层加速度峰值Fig.13 Peak acceleration responses of each floor under El Centro ground motion

图14 三向加载Taft地震波工况各层加速度峰值Fig.14 Peak acceleration responses of each floor under Taft ground motion
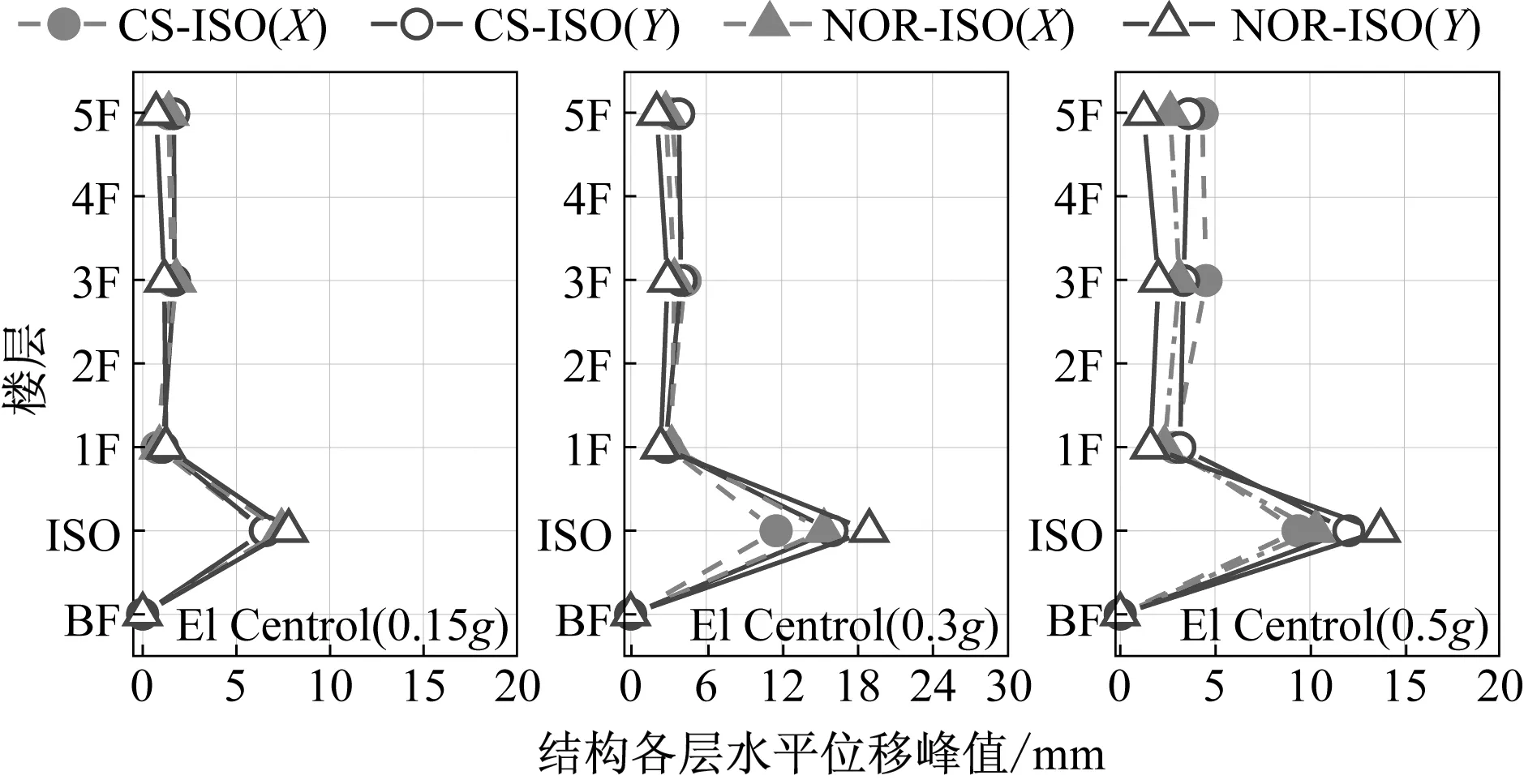
图15 三向加载El Centro地震波工况上部结构层间变形Fig.15 Peak interlayer deformation of superstructure under El Centro ground motion
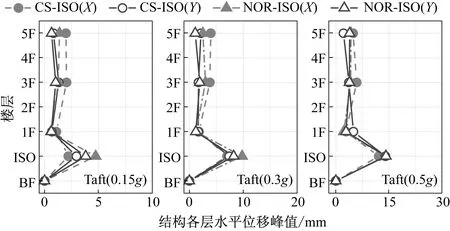
图16 三向加载Taft地震波工况上部结构层间变形Fig.16 Peak interlayer deformation of superstructure under Taft ground motion

图17 三向加载El Centro地震波工况上部结构水平位移峰值Fig.17 Peak horizontal displacement of superstructure under El Centro ground motion
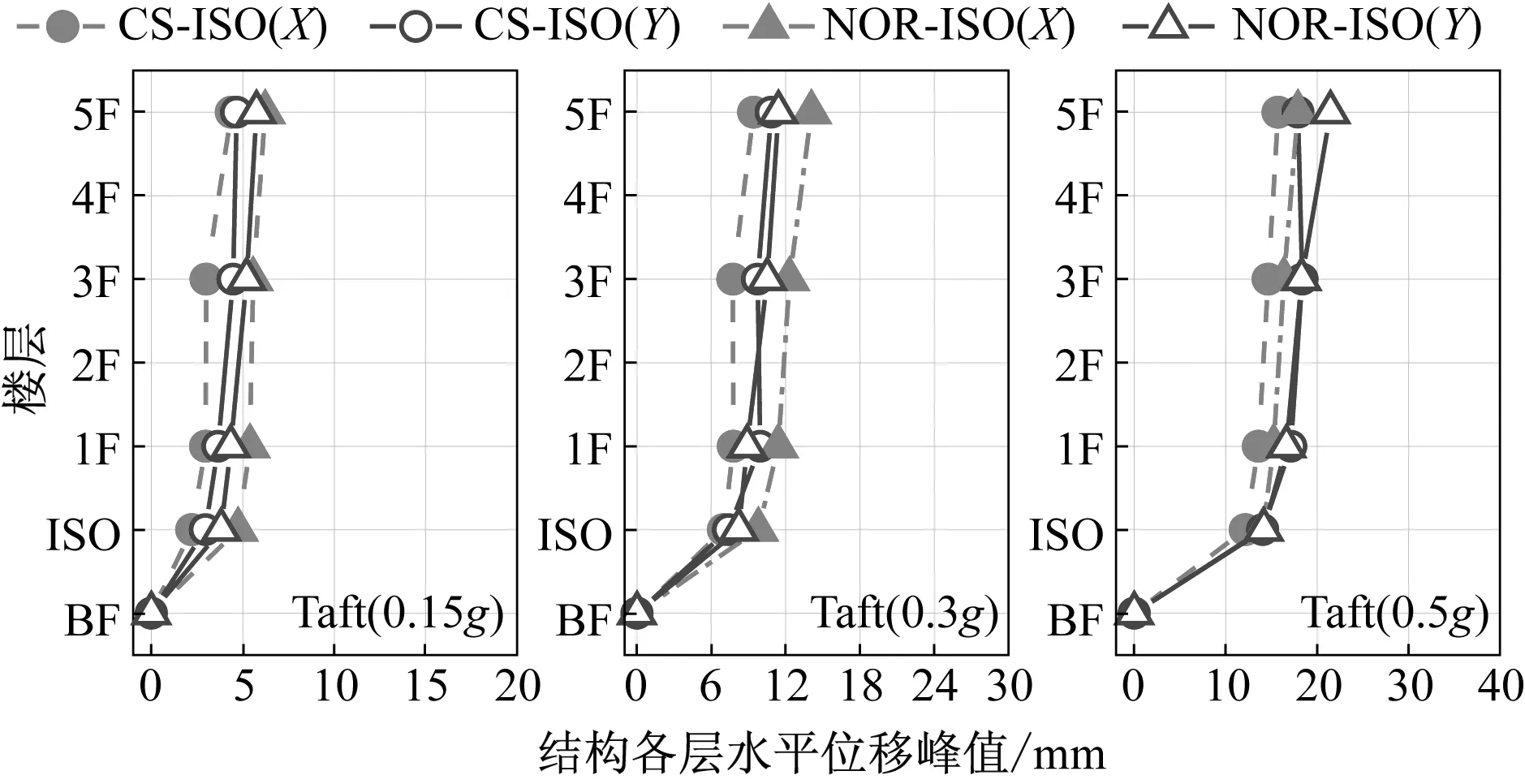
图18 三向加载Taft地震波工况上部结构水平位移峰值Fig.18 Peak horizontal displacement of superstructure under Taft ground motion
4 结 论
本文针对提出的曲面隔震结构这一新型隔震结构体系建立了单质点简化分析模型并对其进行了理论分析,制作了钢框架曲面隔震结构模型,与平面隔震结构模型和非隔震结构模型分别进行了地震模拟振动台试验,得到以下几点结论:
(1)理论分析结果表明,曲面隔震结构体系加速度传递系数和位移传递系数会因为隔震层曲率半径的原因产生新的共振峰值,并且共振峰值出现位置随着结构径高比的变化而变化。曲面隔震结构的加速度传递系数大于平面隔震结构;当结构径高比较小时,位移传递系数小于平面隔震结构,随着结构径高比的增大发生共振,曲面隔震结构位移传递系数逐渐增加并且超过平面隔震结构。合理选择结构径高比,可以在小幅增加隔震结构加速度响应的前提下减小位移响应,控制隔震层位移。
(2)曲面隔震结构模型加速度响应相对于平面隔震结构有所增加,但是显著小于非隔震结构;曲面隔震结构模型隔震层位移及上部结构整体位移均小于平面隔震结构,综合考虑结构层间变形和结构各层水平位移峰值,曲面隔震结构倾覆摇摆运动小于平面隔震结构。
(3)由于曲面隔震结构支座倾斜布置,支座的竖向刚度在水平方向产生一个分量,使得曲面隔震结构隔震支座的滞回曲线相对于平面隔震结构更加饱满。
本文的研究对象主要针对民用建筑展开,今后将进一步开展核电站等重要建筑的曲面隔震地震响应控制研究。

