基于基尼系数校验的电网年度投资方案优选实践

马倩，陈黎军，王璟，姜念，姜文建

（1.江苏省电力公司，南京 210024；2.无锡市供电公司，江苏 无锡 214101；3.天地电研（北京）科技有限公司，北京 102206）

0 前言

随着电网公司进入特高压、大电网、高负荷时代，电网投资规模保持高位运行，对投资决策提出了挑战[1]。电网投资管理是电网企业实现可持续发展的重要基础工作[2,3]。省级电力公司一般下设多个分分公司，对于每个分公司具体应该根据什么方法进行分配，分配多少投资额，都缺乏相应的实际方案和理论支撑。面对这一实际问题，提出电网年度投资计划方案优选体系。

1 年度投资计划方案优选思路

1）初定年度投资总额。以投资效益为着眼点，选取售电量等指标，初步给出全省投资总额以及地市公司分摊投资额。

2）确定投资优先级。根据负荷、容载比等指标确定各地市、各电压等级的投资排序，定性给出投资需求的轻重缓急。

3）判定投资合理性。以投资分配的公平性为主要考量，使用基尼系数衡量投资分配的公平性，采用多目标多约束条件求解最小总和基尼系数的方法得出最终投资分配方案。

2 年度投资计划方案优选体系

2.1 年度投资总额预测

利用统计分析软件的相关性分析模块对售电量-年度投资进行相关性分析，利用线性回归模块建立两者的线性回归模型，然后利用线性回归法进行全省售电量预测，并按照上一年度各地市售电量占比，得出各地市分公司售电量，最后利用售电量-年度投资线性回归模型，计算各地市年度投资初始分配，计算流程见图1。

图1 年度投资总额计算流程

2.2 年度投资优先级排序

根据负荷增长情况对地市总投资进行优先级排序，综合考虑现状供电能力和负荷增长水平，按照负荷增长率越高且供电能力弱的区域，投资优先安排的原则。根据各地市分公司现状容载比曲线与网供负荷增长率曲线数据，进行合理数理变换，创新从两者的偏离度对220 kV投资、110 kV投资进行优先级排序，二者间的偏离距离越大，说明容载比偏离网供负荷增长率越大，即网供负荷增长率较低，而220 kV容载比却很大，对于此类地市投资优先级低。

2.3 投资合理性分析

经过研究，优选单位投资增售电量、220 kV容载比、110 kV容载比等作为投资控制指标，利用熵值法确定各指标的权重，然后绘制各控制指标的洛伦兹曲线，并根据该曲线计算各控制指标的基尼系数，根据各控制指标权重进而求得总和基尼系数，最后利用单目标多约束条件规划求解最小基尼系数，得出各地市分公司最优投资分配分按，计算流程见图2。

图2 年度投资合理性分析流程图

2.3.1 投资分配思想

洛伦兹曲线由美国统计学家马克斯.洛伦兹提出，用于研究国民收入在国民之间的分配问题。洛伦兹曲线将人口按收入由低到高进行排序，以横轴和纵轴分别表示人口累计百分比和收入累计百分比，计算任意累计百分比的人口得到的收入累计百分比，见图3中的LC。

图3 洛伦兹曲线

基尼系数由意大利经济学家基尼提出，是根据洛伦兹曲线、绝对平等曲线和绝对不平等曲线定义的一个比值指标，用于定量分析收入分配的不平等程度。

基尼系数G见式1：

式中：SA表示绝对收入分配绝对平等曲线OC与洛伦兹曲线LC围成的面积；SB表示洛伦兹曲线LC与收入分配绝对不平等曲线OXC围成的面积。

2.3.2 基尼系数控制指标及其权重

综合考虑了指标的科学性，数据的可得性，选取单位投资增售电量、220 kV容载比以及110 kV容载比等三个指标对初始投资额分配方案进行优化。

采用熵值法确定指标权重以反映各个指标对投资额分配影响的重要程度。这里假设表示第i个地市的初始投资分配额，zij表示第i个供电企业的第j个指标的实际值，则第i个地市的第j个指标的单位投资额表示为：yij=xi/zij。由此，得到这里，pij表示第j个地市在该指标所占比重。于是有：

式中，ej表示第j个指标单位投资额的信息熵。于是，得到：

式中，wj表示第j个指标的权重，j=1，2，…，m。这里m表示指标数目，在本分配模型中m=3。

2.3.3 绘制洛伦兹曲线

首先计算各个地市单位控制指标的投资额（洛伦兹曲线中各点的斜率，即各地市的投资额/控制指标值），然后将所得数据从小到大排序，并计算排序后各地市的投资累计百分比和各控制指标累计百分比，进而绘制各地市投资和控制指标的洛伦兹曲线。由于容载比越小，所能承受的投资增幅却越大。为了保证后面各个地市在洛伦兹曲线上排序标准的一致性，这里特对容载比指标进行倒数处理。

2.3.4 计算基尼系数

计算排序后各地市投资的累积百分比和各控制指标的累积百分比，采用梯形面积法计算出各控制指标的基尼系数，计算公式为：

式中，j为各个控制指标编号；i为地市编号；Gj为基于某一指标j的基尼系数；Xj(i)为指标j的累积百分比；Mj(i)为第i个地市j指标值；Yj(i)为基于指标j的投资分配量累积百分比；Wi为第i个地市的投资额度；n为地市个数；当i=1 时，(Xi-1，Yi-1)视为 (0，0)。

2.3.5 求取最小基尼系数目标函数：

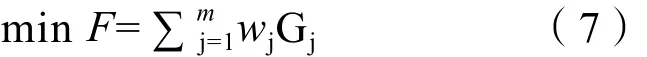
式中：F为目标函数；wj指标j权重；Gj指标j基尼系数；

约束条件包括：总投资额调整幅度的限制；单个地市投分公司资额调整幅度的限制；调整后各控制指标对应的基尼系数小于等于调整前的基尼系数(基于各指标的投资额分配公平性不变差)；优化后每个基尼系数控制指标的洛伦兹曲线上各地市排序不能发生变化。

3 算例分析

本文以某省级电力公司为研究对象，该公司下辖5个地市供电分公司。部分地市基础数据见表1。

表1 地市分公司基础数据

根据基础数据，利用统计分析软件计算得出售电量与年度投资相关系数为0.9261，为高度相关正相关，可以建立回归模型。因此，使用线性回归模型得到售电量-年度数学模型，计算2017年全省售电量预测值，再分摊到各地市分公司，从而得到地市2017年投资初始分配见表2。

表2 地市分公司2017年预测数据

以220 kV电网为例，得到各地市容载比、负荷增长率曲线以及电网投资排序见图4、图5。

图4 地市分公司220 kV容载比、负荷增长率曲线图

图5 地市分公司220 kV电网投资排序图

根据信息熵原理，指标的信息熵越小，表明指标值的变异程度越大，提供的信息也越多，则其权重应越大，反之权重越小。从投资额分配的角度，若某个指标的单位投资额的地区差异越大，其熵权值就越大，对分配的影响也越大。根据上文公示（2）、（3）计算个指标控制权重，见表3。

表 3 各控制指标权重计算表

计算各个地市分公司控制指标的投资额（洛伦兹曲线中各点的斜率，即各地市分公司的投资额/控制指标值），然后将所得数据从小到大排序，并计算排序后各地市的投资累计百分比和各控制指标累计百分比，进而绘制各地市投资和控制指标的洛伦兹曲线。按照熵权值权重，合成基尼系数，见表4初始基尼系数。

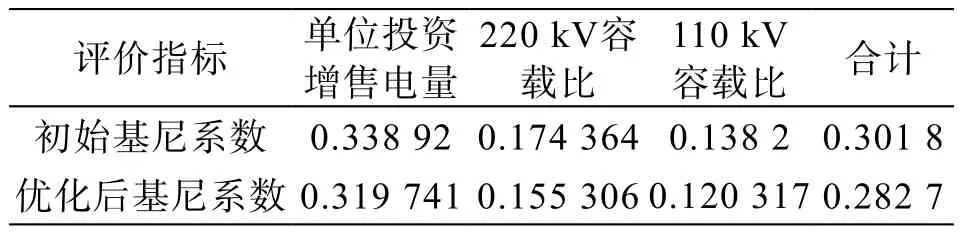
表4 基尼系数计算表

按照初始分配的投资，基尼系数为0.301 8，属于相对合理水平。为了取得满足地区用电需求的基础上，获得最高的公平性，故利用单目标多约束条件规划求解最小基尼系数，得出各地市分公司最优分配投资，按照上文的计算约束条件和边界范围，设定各地市投资调整控制在±15%以内，全省投资控制在±5%以内等条件为约束，优化后计算后获得最优基尼系数为0.282 7，属于比较平均，优化后基尼系数，同时得出优化后各地市分公司投资分配额度，详见表5。

表5 地市分公司优化后投资

4 结束语

本文提出了电网年度投资计划方案优选体系，解决了省级电力公司在实际工作中遇到的实际问题，即下一年度各地市电网投资额分配方案的设计，保证了全省电力资源的优化配置。该优选体系不仅定性给出投资需求的优先级排序，而且定量给出具体投资额度。随着电量预测工作的深入研究，可将更科学的电量预测引入到本体系中。此外，各省级电力公司也可研究更适宜本省实际的控制指标衡量投资分配的公平性。