统计检验力的分析流程与多层模型示例
赵礼 王晖
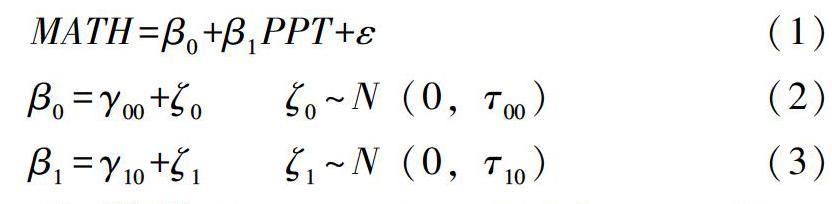
摘 要 影响统计检验力的因素包括研究设计因素、研究工具因素和统计学因素。统计检验力分析是实验设计中非常重要的一部分:先验统计检验力分析可以帮助研究者在实验开始之前确定样本量以节约人力物力;后验统计检验力分析可以在研究完成之后帮助研究者审视研究效力,为后续研究提供帮助。当研究问题或实验设计较为复杂时,可借助Optimal Design设计多阶层统计检验力分析。建议在本科及研究生阶段重视统计检验力分析的教学,在科研中注重统计检验力分析的应用,以优化实验设计并增加研究结果的可靠性。
关键词 统计检验力; 多层分析; 效应量; 假设检验; Optimal Design
分类号 B841.2
DOI: 10.16842/j.cnki.issn2095-5588.2019.05.002
统计检验力(power)是指能正确拒绝错误的零假设(null hypothesis)的概率,是经典统计决策理论和假设检验模式中不可缺少的一部分。近年来,统计检验力分析越来越受到重视,很多学术期刊已经明确要求研究者在论文中提供统计检验力相关内容。但在目前国内的心理学教学与研究过程中,统计检验力分析仍未得到充分的重视。本文着重探讨了统计检验力影响因素和基本分析流程,并且讨论了统计检验力分析中可能遇到的实际问题,并借助Optimal Design来展示如何设计多阶层统计检验力分析,可为当下心理学教学与研究中统计检验力分析与应用提供参考。
1 统计检验力的影响因素
影响统计检验力的因素有很多,主要包括研究设计因素、研究工具因素和统计学因素。
第一,研究设计因素。例如,问卷设计中存在的雷区不只会对研究数据产生影响,也会影响统计检验力。在用词与表述上,研究者不应使用复杂难懂、过于专业的词汇。研究问题不应对被试造成引导性影响,诸如“你是否同意流产——一种谋杀无辜人类的做法——应该取缔?”这样的问题在研究中应当避免。除有意引导外,一些问题可能会因其表意含糊不清而产生歧义。另外,非开放式问题通常比开放式问题的检验力要高,因为开放式问题的答案多样性更高。这些用词与表述问题会使得研究随机误差增加,从而降低统计检验力。并且,由于取悦效应以及研究中可能涉及敏感问题的存在,被试可能会隐藏他们的真实想法,从而导致组间差异变小,进而降低检验力,因此实验中的保密和匿名原则很重要。同样,实验的设计也会影响统计检验力。如果被试间的差异可以得到控制,统计检验力会增加,例如重复测量设计比独立样本设计的统计检验力要高。但是不可单纯追求控制被试差异,在取样过程中,如果抽样框架是错误的(例如包括非理想群体或者理想群体被排除),检验力也会降低。
第二,研究工具因素。例如,量表的精细程度会影响统计检验力。粗糙的量表会造成相关系数的降低(Aguinis, Pierce, & Culpepper, 2009),这类问题是由于研究工具本身所决定的。例如,李克特量表可以用来测量被试的态度(例如1表示非常不同意,5表示非常同意),然而由于量表本身的限制,被试只能在1到5这五个数字中选择,从而造成1.6与2.6或者2.7与3.4之间的比较无法测得,进而降低统计检验力。
第三,统计学因素。(1)数据的范围限制会影响统计检验力。例如,要研究大学GPA和课堂出勤率的关系,如果对GPA的范围加以限制,例如只选取GPA在1~4之间的学生,从而导致研究相关关系的数据受限,会造成统计检验力降低。(2)违反统计假设也会造成统计检验力的降低(Maxwell, Delaney, & Kelley, 2018)。例如对于统计检验力的分析通常基于正态分布的假设,如果违反此假设则需要对统计检验力重新进行解释。非参数检验(例如Kruskal-Wallis H检验)可以应用在非正态分布的情况,并且变量的转换(例如对数转换)可以改变分布的形状使其为正态分布。(3)测量的信度也会影响统计检验力,通常长测验比短测验要更加可靠,因为长测验的变异性较低(Coe, 2002)。例如一个有100个项目的测验的标准差比一个有10个项目的测验标准差要低,所以信度较高,进而统计检验力较高。(4)连续变量二分化会降低统计检验力(Altman & Royston, 2006),此过程会导致很多信息丢失。假设研究学生身高和体重之间的关系,如果把收集到的数据只分为“高”“矮”两类,那么身高和体重之间相关关系的测量会因为身高变量的变异性降低而降低准确性。
2 统计检验力分析的组成部分
统计检验力分析的主要组成部分为:效应量、样本量、第一类错误率(α)和第二类错误率(β)。各成分对统计检验力的影响在已有文献中已有不少讨论与总结(参见吴艳,温忠麟,2011;
温忠麟,范息涛,叶宝娟,陈宇帅,2016;
郑昊敏,温忠麟,吴艳,2011),在本文中将不做重复说明与讨论,只在说明此四部分间基本关系的基础上,再做一些补充。
四成分之间的基本关系如下:(1)效應量和样本量结合可得非中心参数,即零假设样本分布和备择假设样本分布之间的区别。效应量可影响统计检验力,两总体分布的差异可以影响效应量,进而影响统计检验力。当差异增大时,统计检验力增大,反之亦然。(2)样本量越大则统计检验力越大。(3)随着第一类错误率的增大(例如从0.01到0.05),第二类错误率会降低,所以统计检验力(1-β)会升高。(4)与使用不同水平的情况类似,使用单侧检验或者双侧检验也对统计检验力有影响。在同一自由度下,单侧检验比双侧检验要更加具有统计检验力。(5)当变异性增大时,统计检验力会变弱。例如由于影响被试间差异的因素得到了控制,重复实验设计的统计检验力更高。
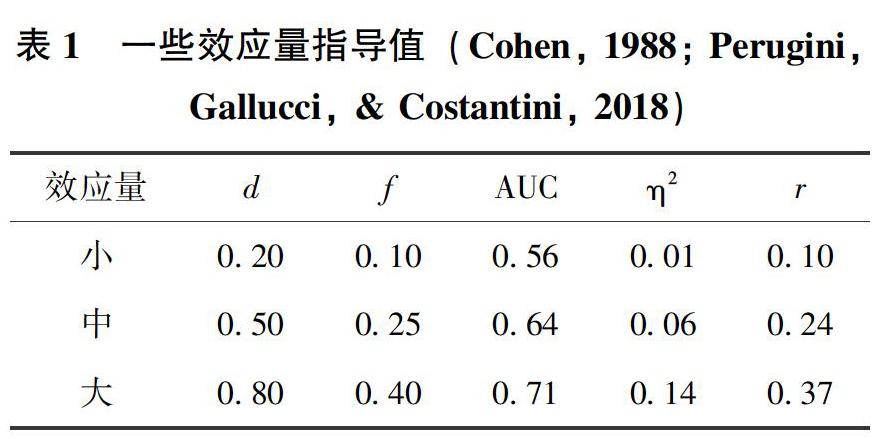
在计算效应量时,观察值(例如1,2)和变异性(例如s)都假设与其真实的参数值(例如μ1,μ2和σ)相等。然而这些真实的参数值很难测得,所以需要估计效应量的值。Howell(2017)提到三种估计效应量的方法:(1)根据先前的研究来决定效应量。具体来说,先前的研究可以提供样本均值和标准差的相关信息,这些信息可以用来作为其他研究中假定可以体现实验处理效应的参数值的参考。(2)在没有相似的先前研究时,效应量的估计则应建立在个人评估的基础上,即研究者主观认为的重要差异的大小(μ1-μ2)。假如研究者想研究一种减肥药,他们决定此种减肥药有效的标准为可以使个体减重5 kg,那么减肥前后的差异(5 kg)就可以用来计算效应量。此选定的差异值可以在正式实验之前通过试验研究(pilot study)来获取经验。例如在社会心理学研究中,研究者经常会研究一些特别新奇的问题,所以他们会在正式研究之前来做试验研究得到可能有实验处理效应的差异值。这个方法不仅可以用来估计效应量,也可以帮助研究者找出错误,从而避免人力物力的浪费。(3)Cohen指导值(表1)(Cohen, 1988, 1992)。
根据不同的效应量水平,研究者可以计算出在某一显著性水平下达到某检验力的样本量的范围。通过10000个研究的元分析发现平均效应量为0.5(Lipsey & Wilson, 1993),一般推荐研究者为达到足够统计检验力的效应量为0.8(Lenth, 2001)。
在以上三种方法中,方法(1)是最为推荐的,当方法(1)和方法(2)都不可用时才根据方法(3)来估计效应量,其原因为此方法中三个水平在一定程度上说为任意制定的(Howell, 2017)。并且Lenth(2001)提出研究者不能只依據计算效应量时的分子和分母的比,也应依据分子和分母本身的数值,因为在先前提到的减肥例子中,研究者不仅应该注重被试服药前后体重的差和样本标准差的比,也应注重被试服药前后体重本身数值的差,更进一步地说,应注重服药前后体重本身的数值。
3 统计检验力分析的两大类型
3.1 先验检验力分析
统计检验力分析是实验设计中的重要的一部分,此分析可以帮助研究者更加深入地思考如何开展该研究,例如思考如何对实验设计进行优化。由于假设检验在社会和行为科学中的实证研究有着非常广泛的应用,在实验研究开始之前研究者通常要对研究做出统计检验力分析来确定能够检测到统计学差异的必要样本量(吴艳,温忠麟,2011)。一些研究人员不重视对研究进行统计检验力分析,他们在研究的过程中发放数以百计,甚至数以千计的问卷来收集数据,然而事实上,这些研究不需要如此之大的样本量,这样就造成了人力物力的浪费,然而这些浪费只需要进行先验检验力分析(priori power analysis)就可以避免。所以,一个合理的样本数量在实验设计中是非常重要的,特别是在经费紧张或者需要人类作为被试的情况下。
3.2 后验检验力分析
后验检验力分析(post-hoc power analysis)是在数据收集和分析之后进行的统计检验力分析。当样本量和效应量(effect size)都已知的情况下,统计检验力可以在某个指定的显著性水平(significance level)(例如0.05,0.01)下计算得到。很多科学家推荐进行事后分析,特别是在研究结果不显著以及效应量分析为中和大时(吴艳,温忠麟,2011;Lenth, 2001)。
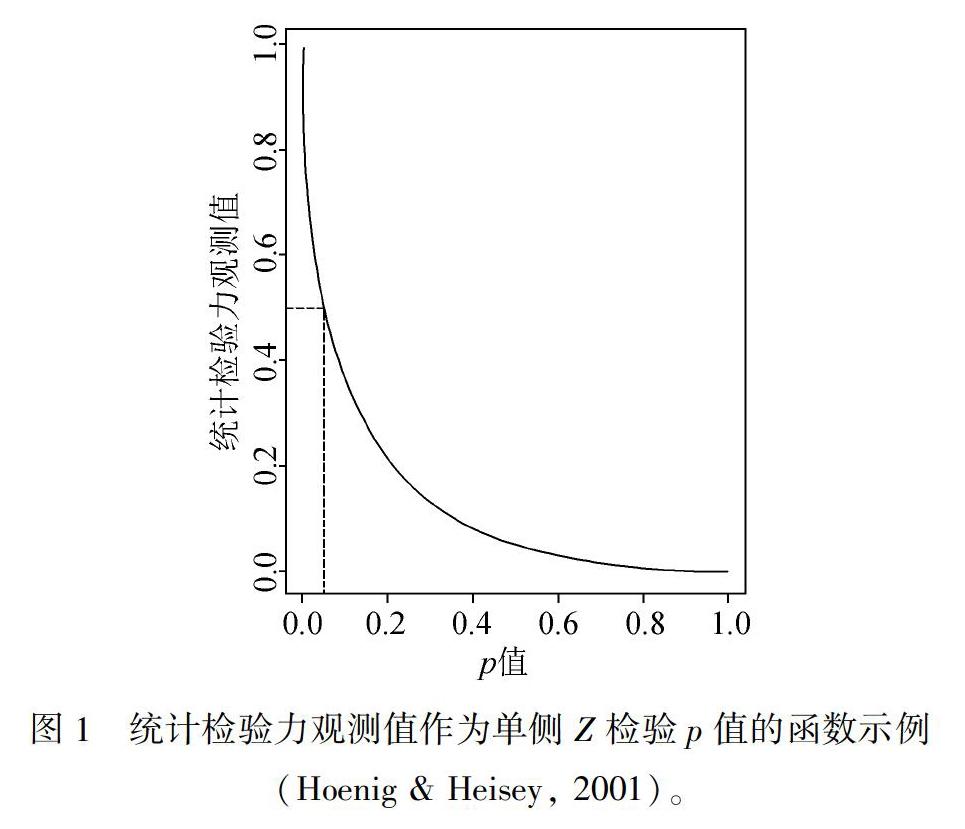
然而,在实际操作中存在不少不恰当使用后验检验力分析的情况。一些研究者认为统计显著性未达到(例如,p>0.05)且基于效应量观测值计算得到的统计检验力值较高的情况为零假设为真提供了证据,然而这种后验检验力分析是不正确的。Hoenig和Heisey(2001)指出统计检验力值是p值的1∶1函数,一旦得知p值,那么计算所得的统计检验力值也就不再提供新的信息。并且此1∶1函数使得非显著p值与低统计检验力值相对应(图1)。当p值为0.05时,相对应的统计检验力值为0.5。当p值增大时,统计检验力观测值则会降低,所以拒绝零假设的同时又有高后验检验力值的情况是不可能的。例如,如果统计检验力值1 为0.4,统计检验力值2 为0.2,基于图1它们分别对应的p值大约为0.075和0.225。所以越高的统计检验力值代表了越大拒绝零假设的几率,而不是为证明零假设为真提供更多的证据。
后验检验力分析的另一个应用为得出可检测效应量(detectable effect size),此效应量可根据变异性和预期统计检验力(例如0.8)计算而得。此后验检验力分析应用的支持者认为根据此方法得到的效应量为真实效应量的上限,即真实的效应量越是接近可检测效应量,那么零假设为真的可能性则越大。然而使用后验检验力分析来计算可检测效应量是不科学的。第一,在同等显著性水平下,若两个实验的结果均不显著、两总体均值差和样本量均相同,且如果(假设为Z检验)Z1>Z2,则标准差σ1>σ2。因为可检测效应量可以通过预期统计检验力(例如0.8)和观测标准差的值(例如σ1,σ2)计算而得,那么第一个实验的可检测效应量应小于第二个实验的相应值,又由于σ1<σ2,那么第一个实验中的总体均值差要小于第二个实验的相应值。因为Z1>Z2且具有统计显著性的两总体均值差是真实差值的上限,那么真实差值越接近具有统计显著性的差值,则拒绝零假设的可能性越大。第二,如果两实验在同等统计显著性水平和样本量下都有非显著的实验结果,且Z1>Z2,那么估计效应量应为:效应量1>效应量2,假设两实验的标准差相等,那么要想达到理想的统计检验力水平,可检测效应量应相等。所以越接近真实效应量的值越代表能拒绝零假设。另外,用基于标准差观测值来计算可检测均值差异也是不可取的,因为我们也应考虑到标准差的变异性。
在研究完成之后再修改统计检验力是很难的,后验检验力分析永远不可以代替事前分析。尽管对于事后分析的结果有时会有误解,但是如果研究者可以正确解释该结果,那么对未来的研究是非常有利的,例如研究者可能得出使用不同的显著性水平更加合适(用0.05而不是0.01)或者发现整个实验设计存在缺陷而需要重新设计。
3.3 存在的问题
在研究者为复杂实验设计做统计检验力分析时可能会遇到一些实际问题。第一,当研究中的自变量有多组时,需要调整显著性水平来控制整体第一类错误率。例如如果使用Holm-Bonferroni方法来控制第一类错误率,那么统计检验力分析则变得复杂起来。Holm-Bonferroni矫正会导致第二类错误增多,因为随着对比对数的增多,统计检验力会降低。例如如果我们需要对比5组,即共有10组对比,当设显著性水平为0.05时,即第一类错误率为0.05,在Holm-Bonferroni矫正之后,α=0.005,可能导致第二类错误率升高。
第二,当模型很复杂时没有统一的方法做出相应的统计检验力分析。例如在混合线性模型(linear mixed model)中,相对来说固定效应(fixed effects)的统计检验力分析比随机效应(random effects)或者固定效应与随机效应混合在一起时要容易分析。并且若考虑到交互作用或协方差,模型会变得更加复杂。然而变量之间的交互对研究者非常重要,但是在统计检验力分析软件中又很难把这一部分添加进去,所以一个可以用来做统计检验力分析的通用且准确的方法是很重要的。
第三,统计检验力分析的结果无法泛化。一旦实验的研究方法、实验设计或者统计方法改变,统计检验力分析就需要重新计算。并且通过检验力分析所得的样本量为理论上可行样本量,但针对某些特定统计方法或实际情境,此样本量可能并不够,例如逻辑回归分析(logistic regression analyses)就需要非常大的样本量,研究者在实验开始之前通过相应的统计检验力分析来确定的样本量对于逻辑回归分析而言可能依然不够。如果样本量不够,由此而得的研究结论则不可信。所以在统计检验力分析之外,研究者也需要考虑到现实因素。另外,因为统计检验力分析是建立在一些假设和猜想上的,且考虑到缺失值的问题,研究者采用的样本数应该比计算而得的样本数在合理范围内稍大。
第四,用来计算统计检验力的软件也存在一些问题:(1)可以用来计算统计检验力的软件有限,通常使用的只有: SamplePower, GPower, PASS, SAS, R和Optimal Design;(2)这些软件大部分都比较昂贵,尽管有的大学提供使用密钥,但是对于老师学生以及很多研究者来说还是无法方便地使用;(3)有一些软件不具备在复杂实验设计下简便计算统计检验力的能力,并且无法在模型中加入交互作用;(4)这些软件可以进行的统计检验力分析类型有限,例如计算多层次统计检验力可以用Optimal Design或者PASS,选择并不多,但前者只有Windows版本,而后者又相当之昂贵。这些因素都限制了统计检验力分析的应用与普及。
4 多层模型统计检验力分析及Optimal Design实现
多层模型,顾名思义涉及到多个层次的数据,例如研究者研究在某一大学中使用幻灯片教学是否对大一学生的数学学习有帮助这一问题,收集到的数据可以分为不同的层次。学生的年龄、性别、数学成绩等都是学生本身的变量,而专业的规模、男女比例、教学所使用教学楼的地理位置等是专业层次的变量,再往高层次来看,学校的规模、地理位置、是否为211或985等因素为学校层级的变量。如此数据在多层模型中发生了嵌套。多层模型分析方法很多,本文着重统计检验力的分析方法。在此以包含一个随机截距和一个随机斜率的多层线性回归模型为例来展示检验力分析的过程:
假设研究者研究在某一大学中使用幻灯片教学是否对于大一新生的数学学习有帮助这一问题,大一新生被随机分配在实验组(使用幻灯片教学)或者控制组(不使用幻灯片教学),研究者设定实验区块(block)为不同学生所学的不同专业。因此,在每一个专业中,新生会随机分配到使用或不使用幻灯片教学的班级中。
如果不考虑协变量,模型使用Raudenbush和Bryk(1992)注释为:
下面使用Optimal Design(Radudenbush, 2011)來展示多层次统计检验力的过程。首先利用此软件及模型可以计算在研究者期望达到的统计检验力水平下所需的样本量。其所需要设定的参数有:(1)显著性水平(α=0.05);(2)预期统计检验力(β=0.80);(3)样本量/簇大小(待决定);(4)被协方差解释的方差大小(R2);(5)被区块解释的方差大小(B);(6)效应量(Δ);(7)效应量变异性(σ2)。
假设研究者预期使得专业为区块可解释40%的结果的变异性,如果使用一个随机效应模型且将效应量变异性设定为0.05时(如果研究者使用的是固定效应模型,效应量变异性应设定为0),并且在先前设定信息的基础上,假如基于试验研究,研究者预期使用幻灯片的学生比不使用幻灯片的学生的表现要好0.2个标准差单位,也就是说设定效应量为0.2。所以,当研究者想在达到0.8的统计检验力并且从每一个专业挑选30个学生的情境下能探测到此效应量时,他们一共需要多少个专业?选择Person randomized trials → multisite(blocked) trials → Power on y axis → power vs. total number of sites(J),将已设定的参数输入Optimal Design,基于图2,可以看出需要28个专业,即一共需要840个被试。
如果考虑协变量,假设基于一个基线调查(baseline survey)(例如IQ,SAT, ACT 等的测量),前测(pretest) 可以解释结果的60%的变异性,如果我们把协变量(IQ)也包括在模型里,可计算得一共需要19个专业(图3),即一共需要570个被试,比不包括协变量时少了270个被试,此模型为:
其中假设IQ可解释学生数学成绩中60%的变异性。
其次,使用Optimal Design还可以计算效应量。例如,设定前测可以解释结果的60%的变异性,如果研究者只能从15个专业中选取被试,并且每个专业选取30人,那么如果想要达到0.8的统计检验力至少需要的效应量是多大?在Optimal Design中需设定的参数为:(1)显著性水平(α=0.05);(2)预期统计检验力(β=0.80);(3)样本量/簇大小(15个专业,每个专业选取30人);(4)被协方差解释的方差大小(R2);(5)被区块解释的方差大小(B);(6)效应量(Δ)(待计算);(7)效应量变异性(σ2)。
在Optimal Design中选择Person randomized trials→multisite(blocked) trials→MDES on y-axis→MDES vs. number of clusters(J)。 当只能从15个专业中选被试时, 效应量大约为0.29(图4)。 如果在此分析中考虑协方差, 效应量大约为0.23(图5)。
5 总结与建议
统计检验力分析是科学研究中重要的组成部分,在研究开始之初,统计检验力分析可以指导研究者确定研究样本量以达到不同的效应量或统计检验力要求。在研究完成之后,统计检验力分析可以帮助研究者印证或审视显著或不显著的研究结果,进而指导研究者不拒绝零假设或者再增加被试量进行进一步的研究。
在本科階段,所使用的教材中假设检验相关章节已非常普及,但与此相关的统计检验力分析、效应量分析等知识章节并不常见,与此相关的教学也并不普及,有一些老师在教学过程中加入此方面相关知识,但讲解也并不深入。学生往往只知当p值在小于0.01或者0.05时拒绝零假设,说明不同实验处理之间存在显著差异,或当p值大于设定的显著性水平时不拒绝零假设,说明不同实验处理之间不存在显著差异。但更进一步,学生不知如何解释p值、置信区间、统计检验力和产生研究结果的原因。之后硕士及博士阶段,随着科研难度及数量的增加,如果研究者不了解统计检验力分析相关知识可能会在研究开始之前无所适从,例如究竟需要多少被试呢?在这种情况下,往往研究者会在未设定样本量的情况下开始实验,直到研究结果显著时停止收集数据,从而影响研究结果的可靠性。因此,从教学上来说,从本科阶段开始,要逐步普及统计检验力分析的重要性及方法,为日后科研工作做出铺垫。
在研究过程中,研究者应谨慎、正确地进行统计检验力分析。它可以帮助科研人员确定样本量的大小,从而避免人力物力的浪费,也可以在一定被试量下得出统计检验力的信息,例如,如果只有75个可用的被试,而所得统计检验力非常低,则没有必要进行这样的研究。在论文发表时或者科研基金申请时,通常都要求研究者说明统计检验力的相关信息,统计检验力的高低虽不是判断研究好坏的唯一标准,但是高的统计检验力是使得研究结论可靠的重要的一方面。
参考文献
温忠麟, 范息涛, 叶宝娟, 陈宇帅(2016). 从效应量应有的性质看中介效应量的合理性. 心理学报, 48(4), 435-443.
吴艳, 温忠麟(2011). 与零假设检验有关的统计分析流程. 心理科学, 34(1), 230-234.
郑昊敏, 温忠麟, 吴艳(2011). 心理学常用效应量的选用与分析. 心理科学进展, 19(12), 1868-1878.
Aguinis, H., Pierce, C. A., & Culpepper, S. A.(2009). Scale coarseness as a methodological artifact: Correcting correlation coefficients attenuated from using coarse scales. Organizational Research Methods, 12(4), 623-652.
Altman, D. G. & Royston, P.(2006). The cost of dichotomising continuous variables. BMJ, 332(7549), 1080.
Raudenbush, S. W & Bryk, A. S.(1992). Hierarchical linear models: applications and data analysis methods. Chicago, IL: Sage.
Coe, R.(2002). Its the effect size, stupid: what effect size is and why it is important. Retrieved May 25, 2018, from: https://www. leeds. ac. uk/educol/documents/00002182. htm.
Cohen, J.(1988). Statistical power analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum Associates.
Cohen, J.(1992). A power primer. Psychological Bulletin, 112(1), 155-159.
Hoenig, J. M., & Heisey, D. M.(2001). The abuse of power: the pervasive fallacy of power calculations for data analysis. The American Statistician, 55(1), 19-24.
Howell, D. C.(2017). Fundamental statistics for the behavioral sciences. Boston, MA: Cengage Learning.
Lenth, R. V.(2001). Some practical guidelines for effective sample size determination. The American Statistician, 55(3), 187-193.
Lipsey, M. W., & Wilson, D. B.(1993). The efficacy of psychological, educational, and behavioral treatment: Confirmation from meta-analysis. American Psychologist, 48(12), 1181-1209.
Maxwell, S. E., Delaney, H. D., & Kelley, K.(2018). Designing experiments and analyzing data: A model comparison perspective. New York: Routledge.
Perugini, M., Gallucci, M., & Costantini, G.(2018). A Practical primer to power analysis for simple experimental designs. International Review of Social Psychology, 31(1), 1-23.
Raudenbush, S. W., et al.(2011). Optimal Design Software for Multi-level and Longitudinal Research. Retrieved May 21, 2018, from http://www. wtgrantfoundation. org.

