基于优化迭代算法的细胞荧光光谱解析

都 月，孟晓辰，祝连庆

(北京信息科技大学 光电测试技术北京市重点实验室,北京 100192)

引言

光谱测量方法具有高效、快速、环保、选择性好、测量精度高等优点，应用领域非常广泛。近年来，为了更加精细地分析细胞特性而进行多色法荧光测量，即使用多种荧光染料标记微粒，并且使用光学扫描显微镜来检测各个荧光染料被激发后所发射的荧光。然而目前所使用的荧光染料的激发或发射光谱较宽，发射光谱范围会有一定的干扰重叠，形成重叠峰，这是定性和定量分析的一大障碍[1]。因此，必须提出有效的理论和方法来分离光谱信号重叠峰。

针对此问题，国内外进行了深入的研究。早期，Kauppinen等[2]提出傅里叶变换的自去卷积技术，被广泛地用到光谱信号的解析，但较难选取合适的去卷积函数，且过程中噪音会呈指数增加，在提高分辨率的同时也降低了信噪比，易产生负旁瓣效应。随着现代信息处理方法的发展，冯飞等[4]利用小波变换对光谱信号进行多尺度分解，结合高斯函数进行光谱拟合，但结果受小波母函数及分解层数的影响较大，且拟合具有较大的随机性；陶维亮等[5]提出将光谱信号转到小波时频域后进行分形维数计算，并利用人工神经网络法进行独立峰提取，可以较高精度分离重叠峰，但效率不高且算法较为复杂。此外，人们发现可以借鉴分析化学中的数学工具来研究光谱信号，为解析光谱重叠提供了新的方式。严彩娟等[6]通过单峰平移缩放对原始峰型进行修正，利用纵向迭代算法实现重叠峰分离；叶国阳等[7]在传统垂线法和切线法的基础上进行改进，提出交点垂线法及比例分配法，提高了峰面积的计算精度，但误差相对较大；朱强等[8]基于函数二分原理，重新规定了迭代方向，但结果受原始峰型的影响较大。上述方法虽对分析化学信号的重叠峰的解析取得了一定的运用效果，但仍具有一定的局限性。因此，为进一步有效分离细胞荧光重叠峰，本文提出一种优化迭代算法，既保证了迭代效率，又提高了分峰的准确性和面积的计算精度。

1 优化迭代算法实现

1.1 重叠峰数学模型

多色分析时细胞样本携带多种荧光染料，可以同时被相同波长的激发光源激发，得到不同的发射光谱。由于目前的荧光染料发射出的荧光具有比较宽的光谱范围，即使每种荧光的发射峰不同，发射光谱范围仍会有部分的光谱重叠[1]。但光谱并不是离散的谱线，而是表现为Gaussian、Lorentz线型等形式的结构相近的谱峰[4]。因此，为方便研究，可假设构成重叠峰的单峰都是相似的。

以高斯模型ae-(x-b)2/2c2作为各个单峰数学模型，其中：a为高斯曲线峰值；b为其对应的横坐标；c为标准差(高斯RMS宽度)。实际情况中，三峰以上重叠的现象较少，所以本文仅对两峰及三峰重叠的情形进行分析。

两峰重叠时，建立对应模拟曲线图如图1所示。定义重叠峰为F，构成重叠峰的单峰分别为A和B，可用下式来表示两峰重叠时重叠峰的构成情况：

(1)

(1)式即为双峰重叠时重叠峰的数学模型。如图1，其中：横坐标表示模拟光谱范围；纵坐标表示荧光强度。

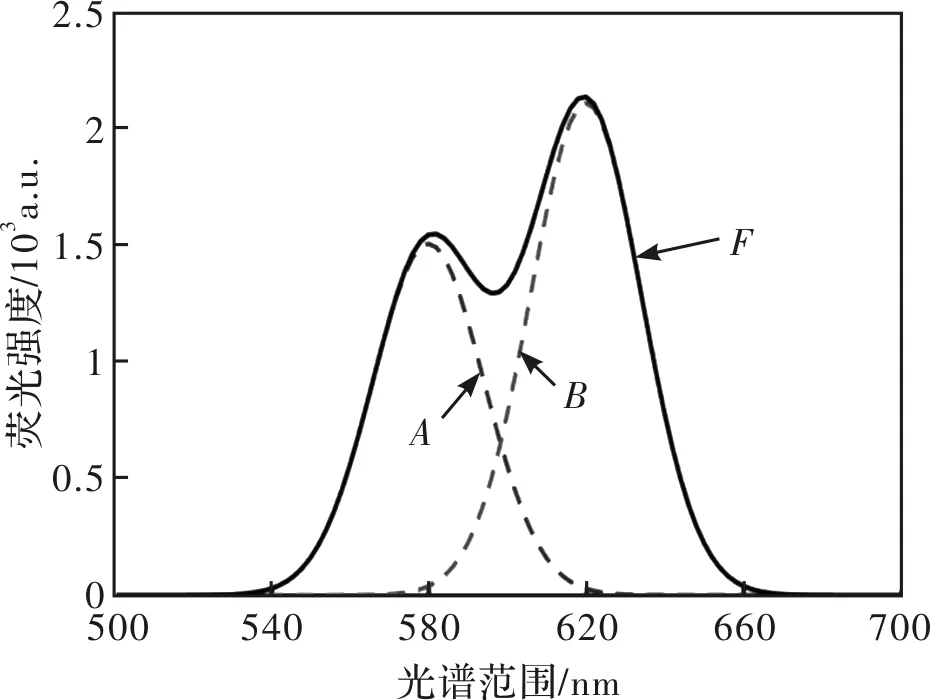
图1 双峰重叠时重叠峰模型Fig.1 Overlapping peaks model of two peaks superimposed

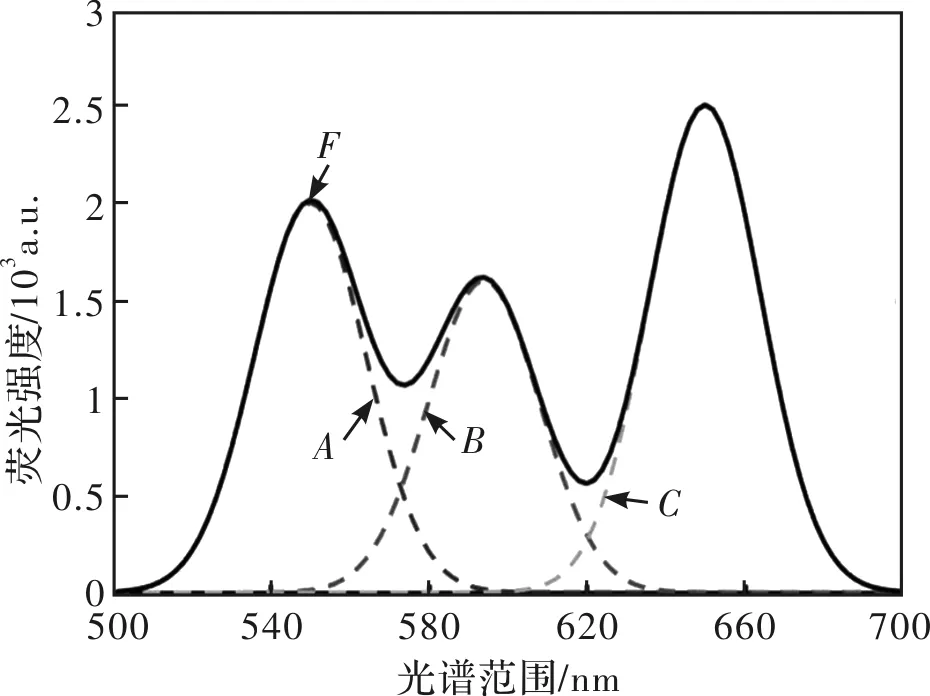
图2 三峰重叠时重叠峰模型Fig.2 Overlapping peaks model of three peaks superimposed

同理，三峰重叠时，建立对应模拟曲线图如图2所示，同时满足(2)式：

(2)

(2)式即为三峰重叠时重叠峰的数学模型。其中A、B、C为构成重叠峰F的三个单峰。

1.2 优化迭代法的算法步骤

为便于描述和理解，本节仅讨论双峰重叠时的重叠峰分峰步骤。根据构成重叠峰的单峰的相似性，重叠峰的前沿和后沿的重叠程度很小，主要重叠部分大部分分布在除前后沿以外的中间部分。故可利用前后沿对中间重叠部分进行修正，通过迭代实现对单峰的逼近[6]。确定每次的构造峰顶点是本文提出算法的关键，具体步骤如下：

1) 寻找重叠峰F的两个顶点，并以此作为第1次构造峰的顶点。重叠峰的前沿即为第1次左构造峰g11的前沿，根据顶点求出纵向修正系数K1，对重叠峰后沿使用系数K1进行修正，得到g11的后沿，即构造出第1次左构造峰g11；用重叠峰F的面积减去左构造峰g11的面积，即得到第1次右模拟峰f12。同理，可得出第1次右构造峰g12和右模拟峰f12，如图3所示。

图3 第1次构造峰和模拟峰Fig.3 Primary tectonic and simulated peaks

2) 在此基础上计算出模拟峰f11、f12的顶点，作为第2次构造峰的顶点。求出纵向修正系数K2，对f11的前沿使用系数K2进行修正，得出第2次右构造峰g22的前沿；同时f12的后沿即为g22的后沿，即构造出第2次右构造峰g12。同理可得出第2次左构造峰g11。最后用重叠峰F分别减去左右构造峰，得到第2次模拟峰f21和f22。前两次得出的模拟峰如图4所示。

3) 按上述步骤继续修正，得到第3次构造峰g31和g32。第3次模拟峰构造方式如下：如果满足g31+g32F，则f31=(g31+g21)/2，f32=(g32+g22)/2，即模拟峰取本次构造峰和上次构造峰的中值；如果满足g31+g32=F，则迭代停止，g31和g32即为所要求的单峰。

4) 重复3)中的步骤，当fn1+fn2无限接近F时，迭代停止。fn1、fn2即为所分离出的单峰。

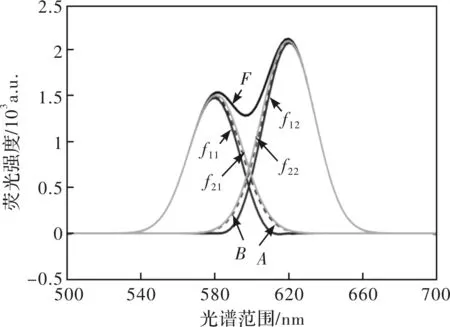
图4 第1、2次模拟峰Fig.4 The first & second simulated peaks

2 算法评价

在重叠峰分离的过程中，分离结果会受单峰的峰高比和原始重叠峰的分离度影响。本文分别模拟了相同峰高比下不同分离度和相同分离度下不同峰高比的重叠峰模型，然后分别算出原始重叠峰在优化迭代算法、原纵向迭代算法及平分迭代算法下的解析误差，进一步对比和验证优化迭代法的分离性能。在分离之前，首先对以下参数进行定义。

1) 峰高比:

(3)

其中HA和HB分别为两单峰顶点高度。

2) 分离度:

(4)

其中:μ1和μ2分别为两单峰位置:ω1和ω2分别为单峰峰宽。R越大，则表明两峰分离越好。通常说当R=1.0时，分离度可达98%。

3) 解析误差:

(5)

其中：S′为计算峰面积；S为真实峰面积。

4) 迭代效率比:

(6)

通常，迭代效率用达到一定计算精度所需的迭代次数来表示。本文定义迭代效率比为相同迭代次数下，进行对比的两种方法的相对解析误差，用来表明迭代效率的提高程度。其中：w1为进行对比的第1种方法达到该迭代次数时的解析误差；w2为进行对比的第2种方法达到该迭代次数时的解析误差。迭代效率比越大，说明后种方法的迭代效率相对前种方法越高。

首先分析了优化迭代算法分离重叠峰的解析误差。为进一步精确地讨论优化迭代法的性能，本次分析使用的重叠峰数学模型均由两高斯峰的叠加而得到。调整高斯函数的各个参数，首先分别计算了在分离度为0.621 8的情况下，峰高比分别为1∶1、1∶2、1∶3、2∶1和3∶1时不同形状重叠峰的解析误差，及在峰高比为2∶3的情况下，分离度分别为0.466 3、0.559 6、0.632 8、0.777 2和0.808 3时不同形状重叠峰的解析误差，分别迭代6次，并与传统纵向迭代法及平分迭代法进行了比较。计算结果如表1、2所示，并作出对应柱状图如图5、6所示。

结果表明，分离度一定时，随着峰高比的增加，传统纵向迭代法的误差较大且会随之增加，平分迭代法的误差稳定在1%之内，优化迭代法的误差相对较小，且维持在0.15%之内；峰高比一定时，随着分离度的减小，传统纵向迭代法的误差较大且也会随之增加，平分迭代法的误差稳定在0.5%之内，优化迭代法的误差相对较小，且维持在0.1%之内。

表1 分离度为0.621 8时的解析结果

表2 峰高比为2∶3时的解析结果

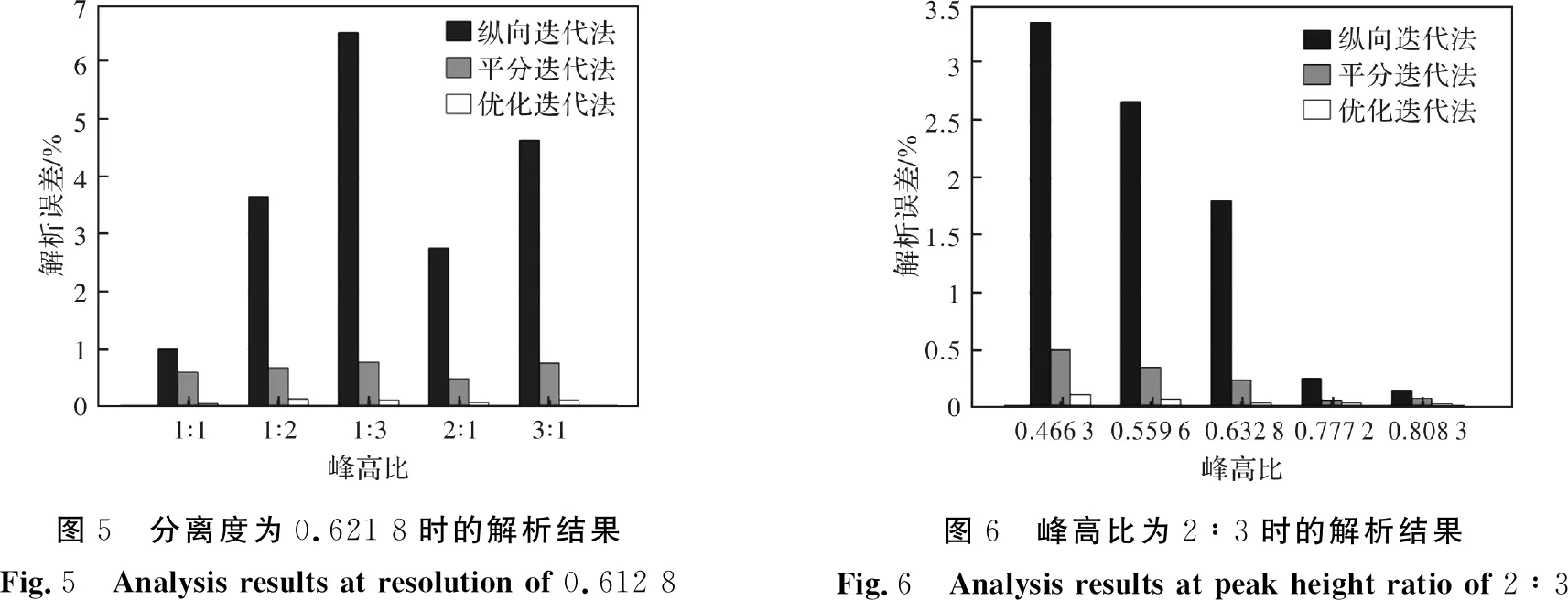
图5 分离度为0.621 8时的解析结果Fig.5 Analysis results at resolution of 0.612 8图6 峰高比为2∶3时的解析结果Fig.6 Analysis results at peak height ratio of 2∶3

其次分析了优化迭代算法分离重叠峰的迭代效率。考虑到实际操作时会遇到三峰重叠现象，本次分析使用的重叠峰数学模型为三个高斯峰的叠加。其中：峰A、B、C的峰高比为4∶5∶6；峰A、峰B分离度为0.621 8，峰B、峰C分离度为0.466 3，峰A、峰C分离度为1.088 1。分别使用优化迭代法、纵向迭代法、平分迭代法分离该重叠峰，根据所得的误差大小来比较三者的迭代效率。三峰重叠时的解析结果如表3所示。由表3可知，由于在第1、2次迭代时，三个方法得出构造峰的方式相同，故有相同的迭代效率；在进行第3至第6次迭代时，使用优化迭代法时明显效率更高；迭代第6次时，迭代效率相对于纵向迭代法和平分迭代法分别提高了88.46%和66.67%。

表3 三峰重叠时的解析结果

此外，还对含有随机噪声时分离重叠峰的迭代效率进行了分析。为方便实验，本次分析使用的重叠峰数学模型为峰高比为3∶4、分离度为0.621 8的两个高斯峰的叠加，解析结果如表4所示。由表4可知，迭代第6次时，迭代效率相对于纵向迭代法和平分迭代法分别提高了57.73%和32.20%。

表4 加随机噪声时的解析结果

3 实验及结果分析

为进一步分析算法性能，使用纵向迭代法、平分迭代法和优化迭代法对实际光谱进行了分离及计算。将淋巴冻干粉与血清混合1 000 μL作为待测细胞，分别加入60 μL异硫氰酸荧光素(FITC)染剂、60 μL藻红蛋白(PE)染剂及30 μL藻红蛋白-得克萨斯红(ECD)染剂将其进行染色。将染色后的细胞充分拌匀后避光静置15 min，并将其放置在共聚焦培养皿上，用共聚焦荧光显微镜观察细胞染色情况，并对其测量到的细胞荧光光谱数据进行曲线拟合。拟合结果如图7所示。

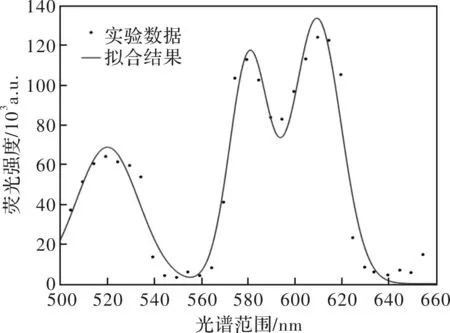
图7 细胞荧光光谱拟合图Fig.7 Fitting results of cell fluorescence spectrum

对数据进行高斯拟合后，分别用纵向迭代、平分迭代和优化迭代法进行解析的结果如表5所示。从表中可知， 迭代6次后，优化迭代法的解析误差为0.36%，优于纵向迭代法和平分迭代法。并且，此时迭代效率相对于其他方法分别提高了90.55%和75.17%。故使用优化迭代法的分离结果更接近实际情况，进而进一步验证了该算法精度。

表5 细胞荧光光谱解析结果

4 结论

针对荧光光谱谱峰重叠现象，本文结合并改进了传统纵向迭代法和平分迭代法，重新确定构造峰的构造方式，提出优化迭代重叠峰分峰新方法。为评估该算法精度，通过模拟不同峰高比和分离度的重叠峰，计算其面积的真实值与解析结果，并同纵向迭代法及平分迭代法进行了比较。结果表明优化迭代算法解析误差稳定在0.15%以内；加入随机噪声后，解析误差可稳定在0.85%以内，均优于另外两种算法。此外分析了该算法的迭代效率，其中三峰重叠情况下，迭代效率在原有基础上提高了66.67%；引入随机噪声时，迭代效率在原有基础上提高了32.20%。对实际细胞荧光光谱中的重叠峰进行了解析，在相同迭代次数下，优化迭代法的解析误差为0.36%，优于纵向迭代法和平分迭代法；且迭代效率分别提高了90.55%和75.17%。此实验进一步验证了优化迭代算法的精度，故可使用该算法对重叠光谱准确进行定性和定量分析。