能量收集型无线传感器网络中高效的能量调度算法
康亚威, 姚彦鑫
(北京信息科技大学 信息与通信工程学院,北京 100101)
0 引 言
能量收集技术使无线设备能够从其环境中的自然资源中获取所需的能量并储存在电池中用于将来使用。这一技术使无线传感器节点的使用寿命大大增加,且提高了能量的利用率[1]。现阶段针对此技术的研究已经成为一个新的研究热点,如何高效利用储存的能量成为一个亟待解决的问题。
由于能量收集具有随机性的特点,能量收集通信系统与传统的通信系统相比需要设计良好的能量调度策略,在随机能量收集情况下使吞吐量最大化。传输过程中,可用能量不能消耗太快,否则可能会由于能量短缺使传输中断。但是假如能量消耗得太慢,电池的能量会大量溢出,引起能量的浪费以及错过下次能量收集机会[2-3]。此类问题在近期的文献中得到了广泛的研究。文献中考虑的情形主要分为在线和离线两部分。离线情况下,虽然现有的研究中提出计算最优离线调度的算法[4-7],但是此类算法计算量大;在线情况下,由于未来的能量到达为未知且随机的,需要动态地确定能量调度方案。
最佳的能量调度方案为传输功率随时间保持恒定,同时确保不会由于电池容量有限而溢出[4]。文献[5]中对于特定的马尔科夫决策过程(Markov Decision Process, MDP)制定了最大化吞吐量的在线解决方案,文献[6-7]中在此基础上与动态规划相结合,研究了在衰落信道下吞吐量最大化的策略,但此类方案只是在特定模型下实现最优,不能紧密贴合实际场景。而当能量收集为全随机模型时,文献[8]中提出了一种应用于一般遍历的平稳过程,证明电池趋于无穷大的渐进最优。文献[9-10]中证明离线最优解可以用多个不同的水位表示,并且将注水法与能量分配相结合,得出离线最优策略。文献[11]中考虑了能量传输成本,用凸优化得出最优策略,但上述策略的计算量都比较大,占用计算空间。文献[12]中提出了一个更为简单的能量调度策略(Fixed Fraction Policy,FFP),用于能量收集为独立同分布(i.i.d.)时的情况,此策略被证明可以与最佳长期平均吞吐量保持恒定的间隙,但此方案仅在能量到达符合独立同分布(i.i.d.)时适用。此外,多用户场景[13]以及MIMO信道预编码策略[14]的离线优化进展明显。
本文提出了一种简单高效的离线能量调度策略。假设能量到达呈周期性变化时,每个周期T看作一个传输阶段,阶段内能量到达近似相等,各阶段之间能量到达符合随机模型。此模型近似可看作太阳能能量收集情况,在一定时间内太阳能辐射近似不变,在下一时间段由于受到云层的遮挡等影响而随机产生变化。本文结合了FFP算法简单高效的特点,针对其只适用于能量收集为(i.i.d.)的特点进行了改进。
1 系统模型
考虑具有能量收集的无线传感器网络节点之间单信道的传输的场景,目标是最大化系统运行时期预期吞吐量。传感器节点配备有限存储容量的可充电电池。假设能量收集发生在每个时隙的开始,信道状态保持恒定不变。每个传输阶段共有T个时隙,每个时隙均进行能量的收集和调度。用Ek表示在第k个阶段的能量收集,且Ek在该阶段的时隙保持不变。在第k阶段的第i时隙结束时,数据到达发射机,发射机通过收集并存储的能量进行数据传输,数据通过静态信道传输至接收机,如图1所示。
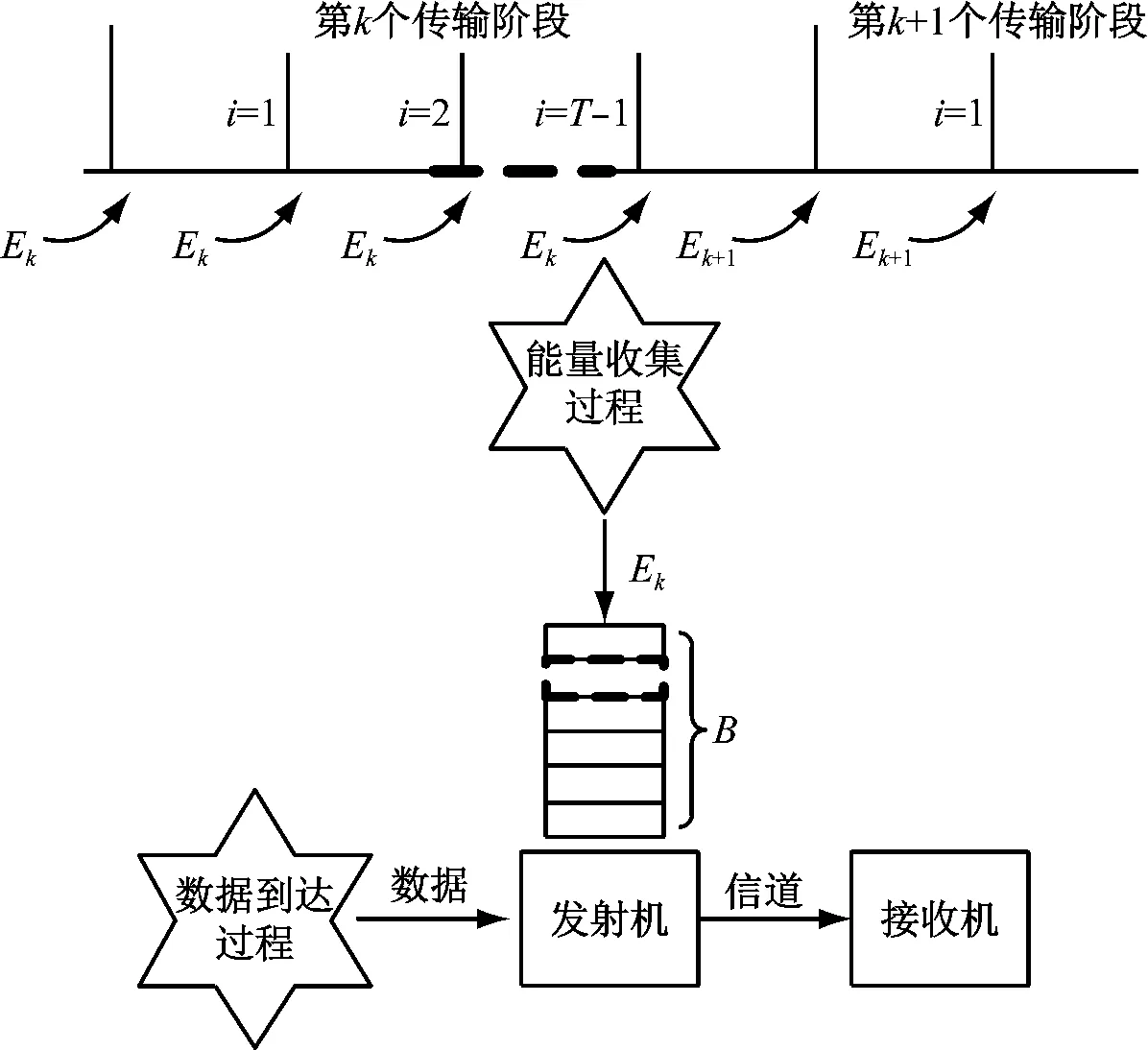
图1 具有能量收集和数据到达的EH通信系统
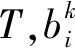
(1)
0≤Ek≤B,k=1,2,…,K
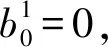
(2)
式中:W为信道的带宽;N0为高斯信道的噪声功率谱密度。对于策略集合P,可以定义当总传输时间为N,且能量收集为E1,E2,…,EN时的总吞吐量为
则同一策略的长期平均吞吐量可定义为
(3)
本文的目标是得出最优的离线能量调度策略以及最大吞吐量,即
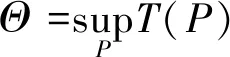
(4)
2 算法实现
由于恒定功率传输数据,且能量没有溢出时系统吞吐量最大,根据FFP策略的理论证明,对于时隙t中电池的现有能量bt取固定的比例q(q∈[0,1])的能量进行数据传输可实现次最优的实验效果,其离线策略pt表示为
pt=qbt,t=1,2,…
(5)
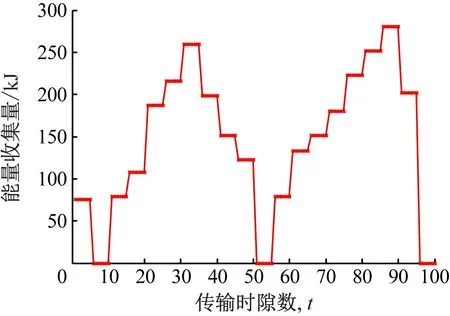
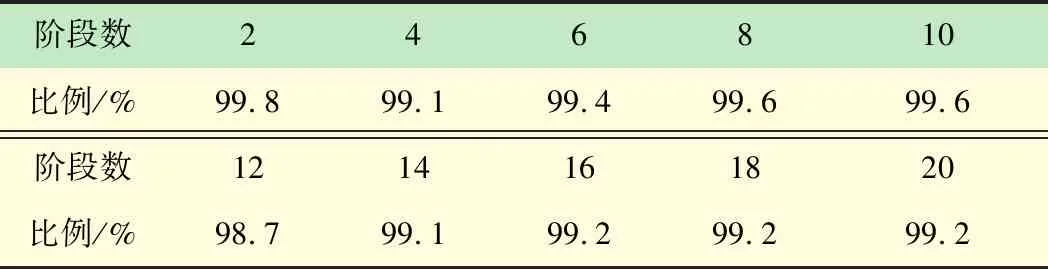
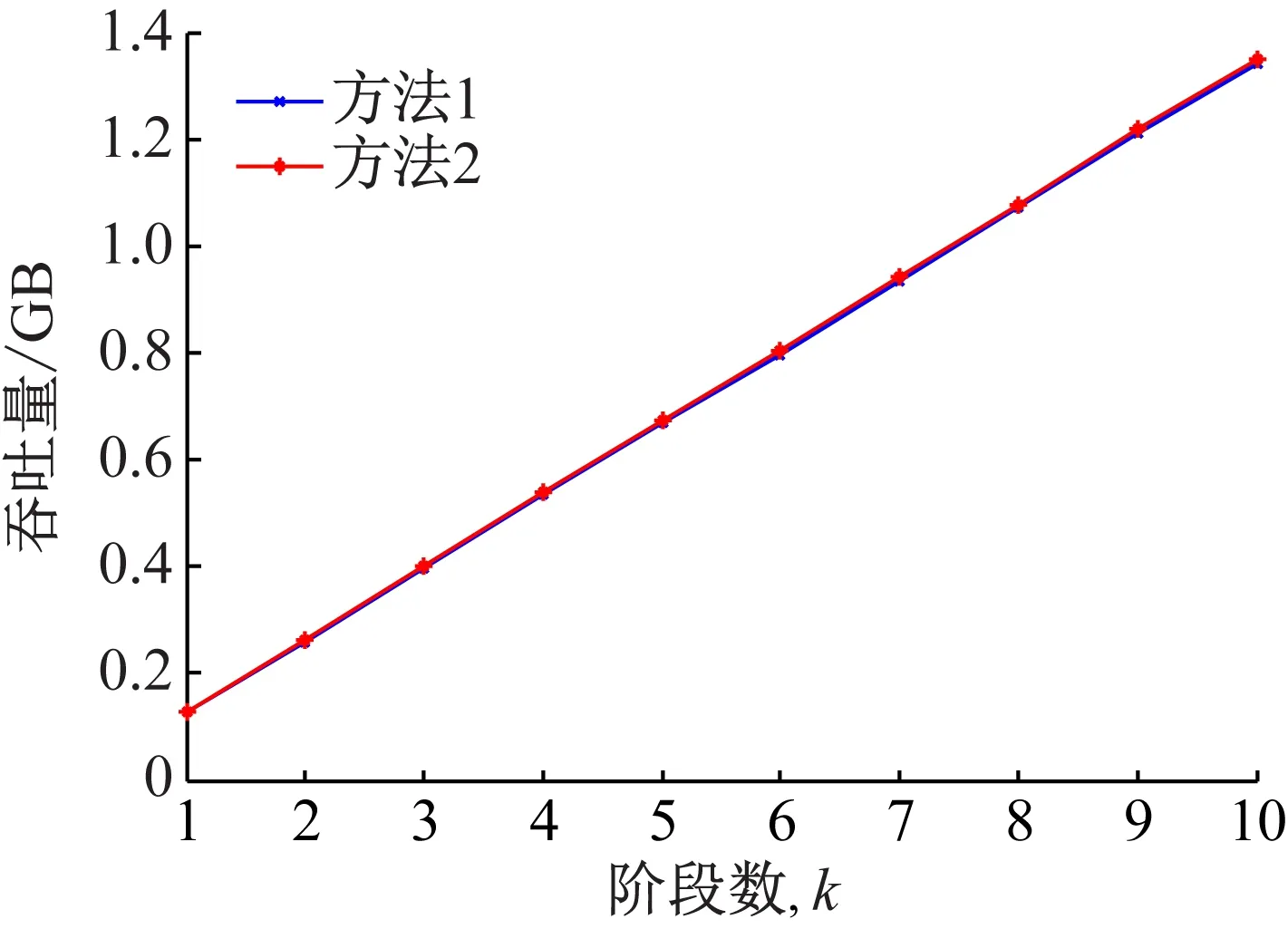
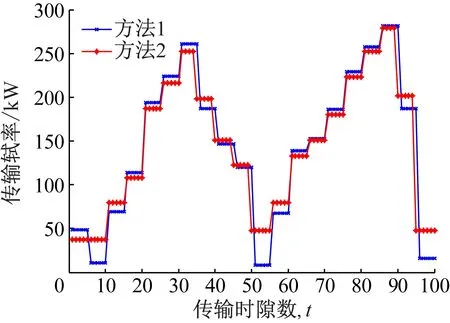
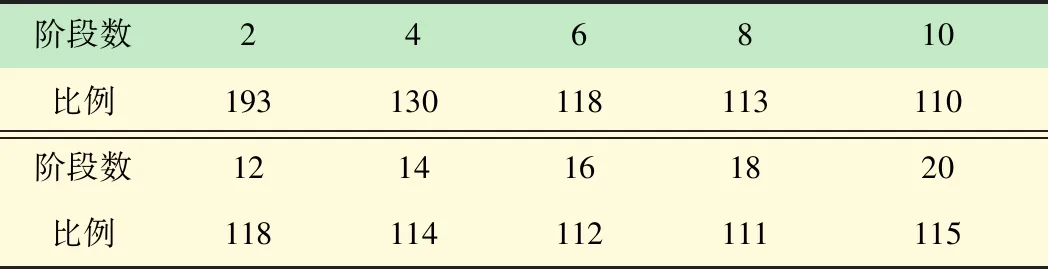
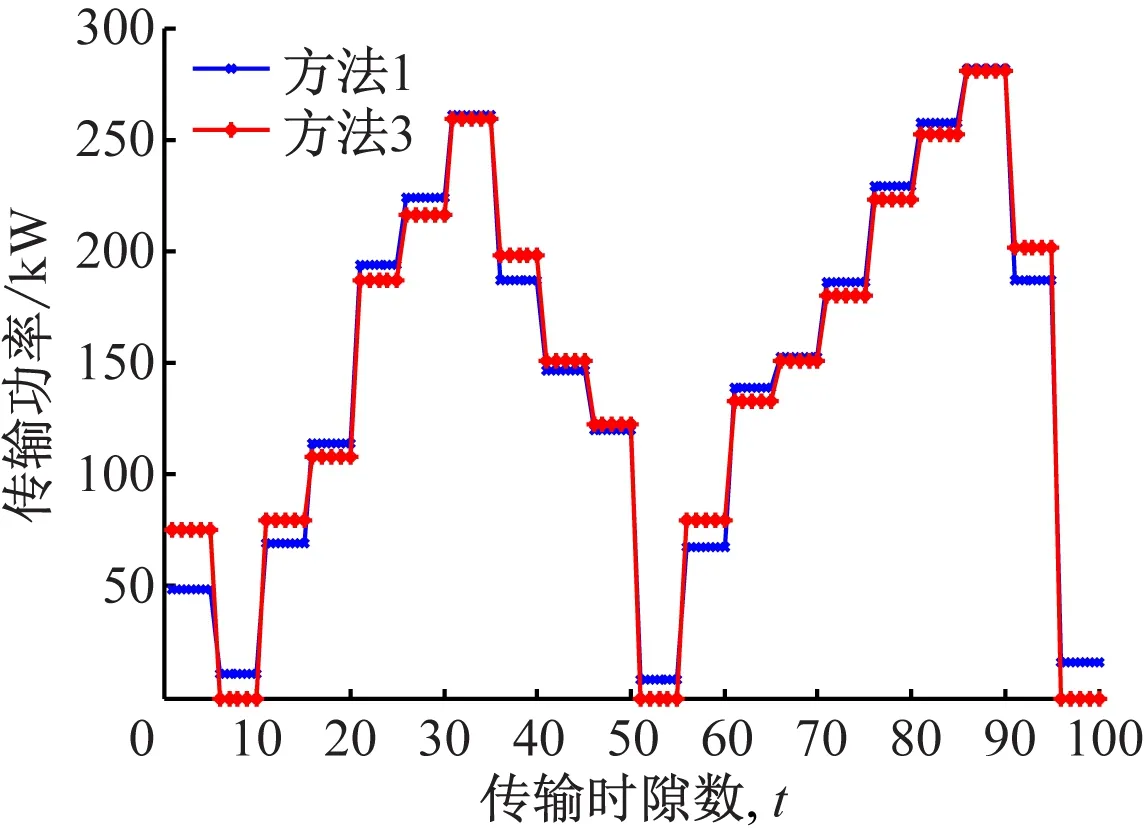
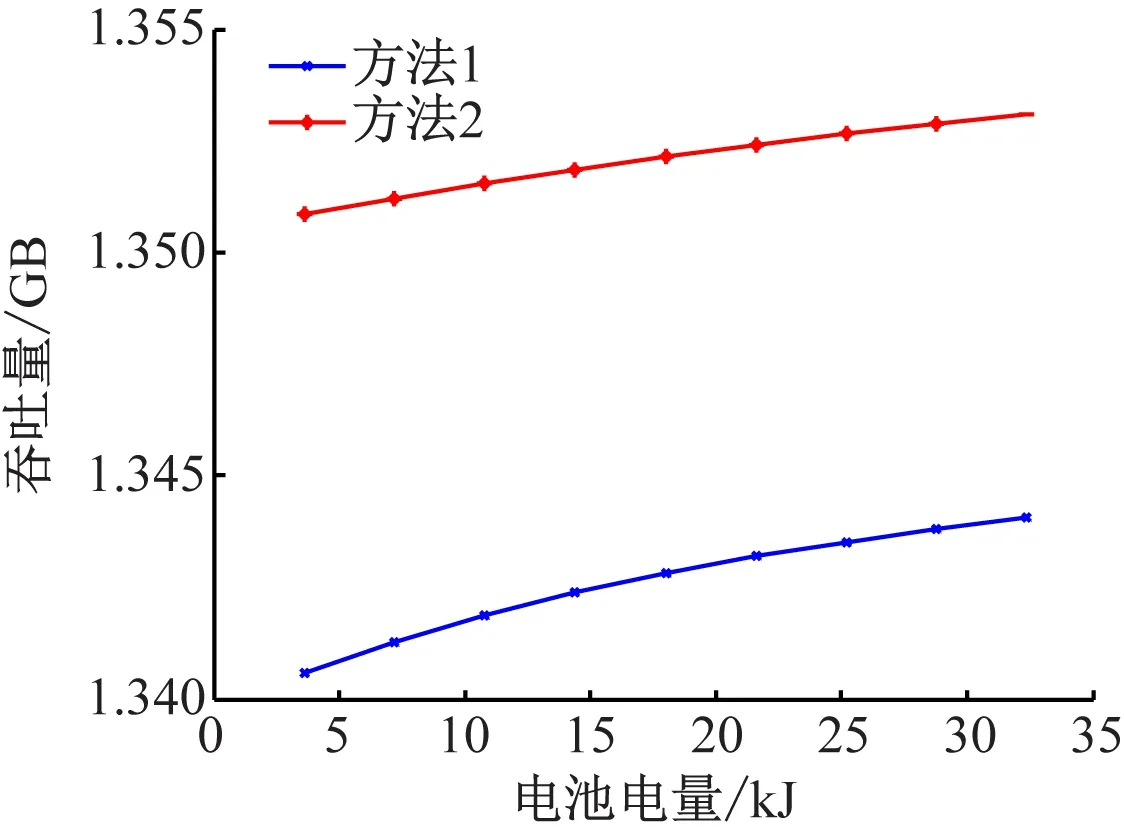
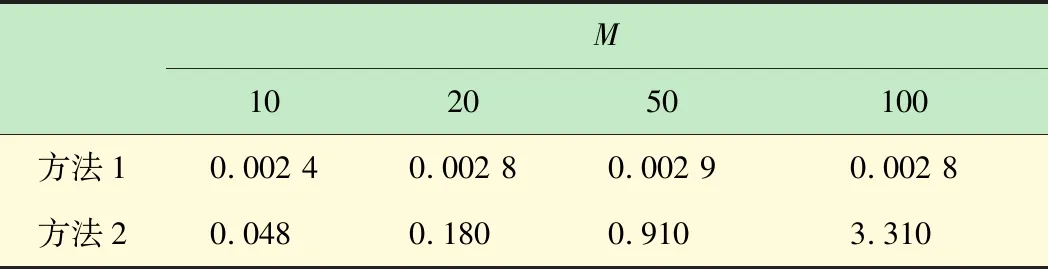
结合本文的模型,当能量收集Ek (6) 由式(6)得出在传输阶段k内能量溢出的限制条件为 (7) 当满足此条件时,可以将第k阶段T时隙的电池状态表示为 (8) 根据式(7)以及(8)可得出当能量溢出时,能量的调度策略为 (9) 为表示方便,将Q定义为 (10) (11) (12) 由式(9)与(11)得出qk的表达式为 (13) 当满足式(13)时,qk的取值可以确定在当前传输阶段能量不发生溢出,即满足式(7)的限制条件。 (14) 根据式(7)且已知能量收集分布,可以将qk取值范围表示为 (15) k=1,2,…,K-1 根据能量收集的分布模型,结合式(13)以及(15)建立qk的取值范围如下: (16) 当进行到传输最后一个阶段,即第K阶段时,能量溢出的条件为式(7),则制定新的能量调度策略,将此阶段按照恒定功率的策略进行传输数据,其传输策略为: (17) 综上,本文的能量收集模型建立以下的能量调度策略: (18) 为了验证文中能量调度策略的性能,将本文算法与最优离线算法[4]和贪婪算法[15]进行对比。为了便于表示,将改进的FFP算法设为方法1,最优离线算法设为方法2,贪婪算法设为方法3。 在数值分析中,使用基于IEEE802.15.4e[16]通信系统的参数。将传输阶段长度设定为1 h,每个阶段共有T=5个时隙,每个时隙时间为12 min,可用带宽W=1 MHz。电池容量B=36 MJ,信道的增益为H=1.655×10-13,噪声功率密度N0=10-20.4W/Hz,则根据式(3)可计算吞吐量。能量到达分布为太阳能辐射监测实验室网站下载的现实数据,此数据近似符合本文的能量收集分布模型。将能量数据对3个算法分别进行仿真,其太阳能能量收集分布如图2所示。 图2 能量到达分布图 将传输阶段分为k=20个阶段,在数据传输过程中,对能量收集的分布使用方法1与方法2进行传输,两种算法在传输阶段内的总吞吐量与阶段数的关系如表1所示。 表1 方法1吞吐量占方法2的比例 由图3可以清晰地得出方法1具有高效的传输效率,在整个传输阶段中,方法1的吞吐量曲线紧贴方法2。当传输阶段k=20时,方法2的吞吐量比方法1高0.01 GB。根据表1可得出方法1在能量随机变化的情况下,传输效率保持稳定,吞吐量约占方法2的99%左右。 图3 方法1与方法2吞吐量对比 根据图4得出,方法1的策略整体上跟随方法2的变化趋势,能量利用率均为100%,但是曲线的趋势仍有背离的部分,例如时隙t=1~10的部分,方法2保持恒定传输,方法1则出现波动,这就是方法1与方法2吞吐量出现差距的原因。 图4 方法1与方法2传输功率对比 其他仿真条件不变,根据能量到达分布,将方法1与方法3进行对比,其仿真结果如图5所示。 图5 方法1与方法3吞吐量对比 由图5可得,方法1相对方法3吞吐量具有明显的提升,在传输阶段中,虽然方法3的吞吐量曲线与方法1的轨迹大致相同,但是吞吐量差距很大。当传输阶段k=20 时,方法1的吞吐量比方法3提升0.178 GB。根据表2可得出方法1其吞吐量较方法3至少提升110%。 表2 方法1吞吐量较方法3吞吐量的提升 根据图6可得两种算法的传输功率趋势大致相同,能量利用率均为100%。但是当太阳能能量到达为0时,方法1为恒定的非0的功率,而方法3的对应时隙的功率则为0,此为方法1与方法3吞吐量出现明显优势的主要原因。 图6 方法1与方法3传输功率对比 图7展示了电池电量B对预期数据传输总量的影响。可见,对于所提出的算法,预期数据传输总量随电池容量B增加而增大。总的来说,方法1的性能约是方法2的99%。 图7 电池大小对吞吐量的影响 (2) 方法2计算量。设电池共M个状态,即单个阶段传输功率可有M种情况。方法2类似于用穷举法将每个阶段可能的传输功率情况进行枚举,找出在有限长的传输阶段下最优的传输策略。当传输阶段为k=N时,方法2中加法的计算次数为2NM,乘法的计算次数为4NM,对数运算的计算次数为NM。 (3) 计算量对比分析。相对来说,对数运算的计算量要大于乘法运算,加法运算的计算量最小。因此,只考虑乘法和对数运算。当电池状态数M=4时,方法2的计算量就必定大于方法1,可以得出电池的状态不仅仅只有4种,当电池的状态越多时,方法1计算量降低便会越大,大大提高了策略的时效性,节省了计算空间。 为了比较方法1与方法2在运算时间上的差距,首先设定电池的状态数M,而后对算法中运算的时间进行对比。由表3的数据分析得知,随着电池状态的增加,方法1运算时间几乎不变,而方法2的运算时间增长迅速。由此可得出,当电池状态越多时,方法1更加节省计算量以及运算时间。 表3 两种算法运算时间 s 本文考虑了能量随机收集的通信系统,其中发射机具有能量收集装置和有限容量的电池。当信道为静态信道时,着力对传输阶段总传输数据最大化问题进行了研究。针对离线优化问题,对文中所述能量收集模型的功率控制在原有FFP算法的基础上进行了改进,确定了次最优的传输策略。其性能可以达到最优离线算法的99%,比传统的贪婪策略性能至少提升约110%,并且分析了改进的FFP算法与其他算法产生吞吐量差异的原因。最后,进行了计算量与算法运算时间的对比,下一步的研究工作是在此基础上找到最优的在线能量调度策略。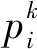
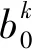
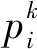
3 仿真实现
3.1 吞吐量分析

3.2 计算量分析
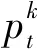
4 结 语

