第二十二届北京高中数学知识应用竞赛决赛试题及参考解答
一、标准田径场被俗称为400米田径场,如下图所示.最内侧跑道由两条86米长的直道和两条半径约为36.3米的半圆弧线弯道构成.每条跑道宽度1.25米,共有8条跑道.一所新建学校,由于面积狭小,不能建立标准田径场,只能建300米的小田径场,它的最内侧跑道内沿全长为300米且和标准田径场比例相同,共有六条1米宽的跑道.
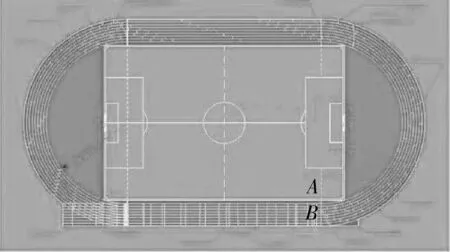
(1)计算小田径场最内侧跑道中一条直道的长度及弯道的半圆弧线的半径;
(2)把田径场完整地放在一个刚好能包容它的矩形中,这个矩形称为这个田径场的“占地矩形”.小田径场设置了百米直道,能否在占地矩形内象标准田径场那样将百米赛终点线设在AB处(如图)?如果不行,线段AB至少向右延长多少米?
(3)如果在小田径场上进行400米比赛,不允许运动员变道,终点为百米赛的终点,最内侧跑道的起点设在百米起跑线处,每条跑道长度按照内侧线长度计算,求第六条跑道的起点位置;
(4)在(3)中给了赛跑路径及计算赛程的要求,也就是给了“模型假设”,你认为对400米赛跑有不尽合理之处吗?
解(1)设小田径场最内侧跑道内沿的一条直线段长度为x米,半圆弧线半径为y米.
由条件可知,2x+2πy=300,x:y=86:36.3,解得:x≈64.49,y≈27.22.
(2)若百米赛终点线设在AB处,在占地矩形的长边可用直线赛道长度为
64.49+27.22+6≈97.71(米),
可见,无法在占地矩形内将百米赛终点线设在AB处.至少向右延长2.29(米).
(3)各条跑道的每一圈长度互不相等,第一道(最内侧跑道)是300米,第六道是
2×64.49+2×(27.22+5)π=332.32(米).
按比赛规定,在400米赛中,既然终点为百米赛的终点,第一道的运动员起点设在百米赛的起跑线处刚刚合适,若第六道的运动员起点也设在百米赛的起跑线处就不合适了,他比第一道的运动员将多跑32.32米.因此,第六条道的起跑点位置应当设在百米起跑线右边32.32米处.
(4)有两个不合理之处.
第一个,每个运动员在自己的跑道上刚好跑完一个完整的弯道全程,而弯道的长度是彼此不同的,也就是任两个运动员在400米赛中的直道、弯道距离都不等,略显不公.
第二个,计算赛程是以跑道内沿长度为准,而实际上,运动员若踩着内侧线跑步就是犯规,于是,若不踩线犯规,运动员就要离开边线一段距离,于是,跑完全程就要多于400米.
二、在1772年,自然学家J.R.Forster首先提出:生物种数量是随着区域的面积扩大而增加的.这是一个最基本的生态学规律.从这之后,一批自然学家走遍全球各地的岛屿,搜集并记录了大量的面积与相应生物种数的数据,它们的生态模式和趋势慢慢地显示出来了,生物种的增加速率出现了降低的趋势.基于大量的统计数据,1920年,O.Anenius给出了物种-面积的幂函数表达式,即生物种-面积模型
S=cAz
(*)
式中A表示岛屿的面积,S表示岛上生物种的数量,常数c和z由观测资料确定,z一般是很小的一个数,通常在[0.2,0.3]的范围内.
因为这个幂函数来自于对观测数据的拟合,仅仅描述了现象,并没有从生物进化上给出解释,所以,有的自然学家对幂函数的模型提出了质疑.尽管遭到质疑,这个函数表达式仍然是一个可供参考的生态学规律.
(1)有人关注林地面积对生物种数的影响,猜想:如果有50%的现存林地被毁掉,将有50%的生物种灭绝.请利用(*)式,在z=0.25的条件下对这个猜想作出判断;
(2)如果岛屿的90%或99%的面积被大海淹没,用(*)式作预报,在z=0.25的条件下将分别有多大比例的生物种保存下来;
(3)依据上述计算结果,分别阐述生物种-面积模型的合理性以及“有的自然学家对幂函数的模型提出了质疑”的合理性.
解(1)将现存林地面积记作A0,毁林后的林地面积为A1,现存的生物种数量为S0,毁坏林地后的生物种数为S1.则有A1=A0-50%A0=50%A0,根据(*)式,有
于是有
即S1=84%S0.即灭绝的生物种数为现存生物种数的16%.猜想是错的.
(2)将现在的岛屿面积记作A0,淹没k%后的岛屿面积为Ak,现在的生物种数为S0,淹没后的生物种数为Sk.则有Ak=A0-k%A,根据(*)式,有
于是有
即岛屿的90%的面积被大海淹没,保存下来的生物种数是原来的56%;岛屿的99%的面积被大海淹没,保存下来的生物种数是原来的32%.
(3)由(1)产生的计算结果告诉我们,虽然随着面积的减少生物种也要减少,但生物种数的减少比例相对面积的减少比例要小很多.一般来说,物种的灭绝是一个极其缓慢的过程,生存面积的变化,首先影响到的是生物种内的个体数逐渐减少(可能成为“受威胁的”物种),如果是继续减少的趋势,这个物种就被看作是“濒危的物种”,再下去将出现物种灭绝.面积的减少最直接的影响是生物种内个体数的减少,至于出现生物种数量的减少(即生物种的灭绝)还需要一个漫长的过程.生物数与生物种数是两个不同的概念,生物数量与生物种数减少情况差别很大.
另外,人们观察记录的数据是在一定面积的封闭区域内(如岛屿)生物种的数量经过漫长时间复杂的进化演替过程后的最终的结果.生物种-面积模型仅仅是对这个最终结果前提下面积与生物种数状况的描述,并没有涉及到生物种演化的具体过程.彼时观察到的数据形成的结论能不能用来表示又经过几百年生物进化后的此时的生物种数与面积的关系?谁也说不准,这样简单地将物种数量归结为面积的大小是不全面的.再看(2)的结论,当海岛面积减少到原来面积的1%时,保存下来的生物种数是原来的32%,这个结论有点出乎意料,在地域较大的情况下也许没问题,当面积较小时,再缩到原来的1%,很难说还会有原来32%的物种.因此,质疑生物种-面积模型是有道理的.

三、在北京地铁4号线的车厢里,到处可见漂亮的弯管扶手,如右图,我们将弯管形状近似地看成是圆弧,已知弯管向外的最大突出有15公分,跨接了6个坐位的宽度,每个座位宽度43cm,求弯管的长度.
解下图是弯管形状的示意图.每个座位宽度43cm,六个坐位总宽度为2.58m.依题意,在右图中,AB=2.58m,CD=0.15m,所求为AB弧长.
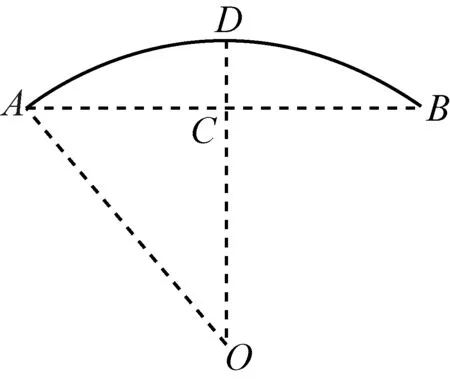
设弧所在圆的半径为r,由图可得
r2=(r-CD)2+AC2=(r-0.15)2+1.292,
得r=5.622(m).
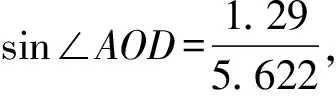
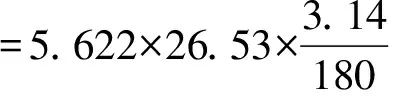
≈2.6032(m).
即弯管的长度约为2.6米.
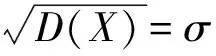
(1)人们直观地认为:用多次测量的平均值来估计μ,要比用一次测量值好.请你通过数学的定量分析予以证明;
(2)如果天平的精度σ=0.05,用天平测量多少次能使估计值的精度达到0.01?
注:在回答问题中,可能要用到随机变量均值和方差的如下性质:
1°设X是随机变量,a是一个常数,则
E(aX)=aEX,E(X+a)=EX+a,
D(aX)=a2D(X),D(X+a)=D(X)
2°设X1和X2是随机变量,则
E(X1+X2)=EX1+EX2
3°设X1和X2是独立的随机变量,则
D(X1+X2)=D(X1)+(X2)
解(1)假设做了n次独立的测量,测量值分别是X1,X2,…,Xn,这n次测量值的平均值是
利用方差的性质,有
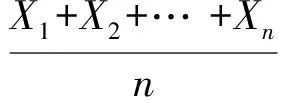
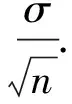
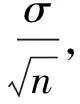
五、有一种病毒在人群中传播,使人群成为三种类型:感染病毒后康复(所有康复者都对病毒免疫),记作R型;没感染病毒但可能会感染病毒,记作S型;已感染病毒,记作I型.病毒防疫部门每周统计一次病毒传播情况,将第n周的感染病毒后康复人群记作Rn,将第n周的没感染病毒但可能会感染病毒人群记作Sn,将第n周的已感染病毒人群记作In.
经长期统计数据发现规律:如果开始时整个人群是S型,那么,第n周的S型人群在n+1周时,其中93%仍为S型,7%为I型;第n周的I型人群在n+1周时,其中65%为I型,35%为R型;第n周的R型人群在第n+1周时仍为R型.
(1)根据已知条件,将前两周各种类型人群发生的概率填在下面树状图的括弧内;
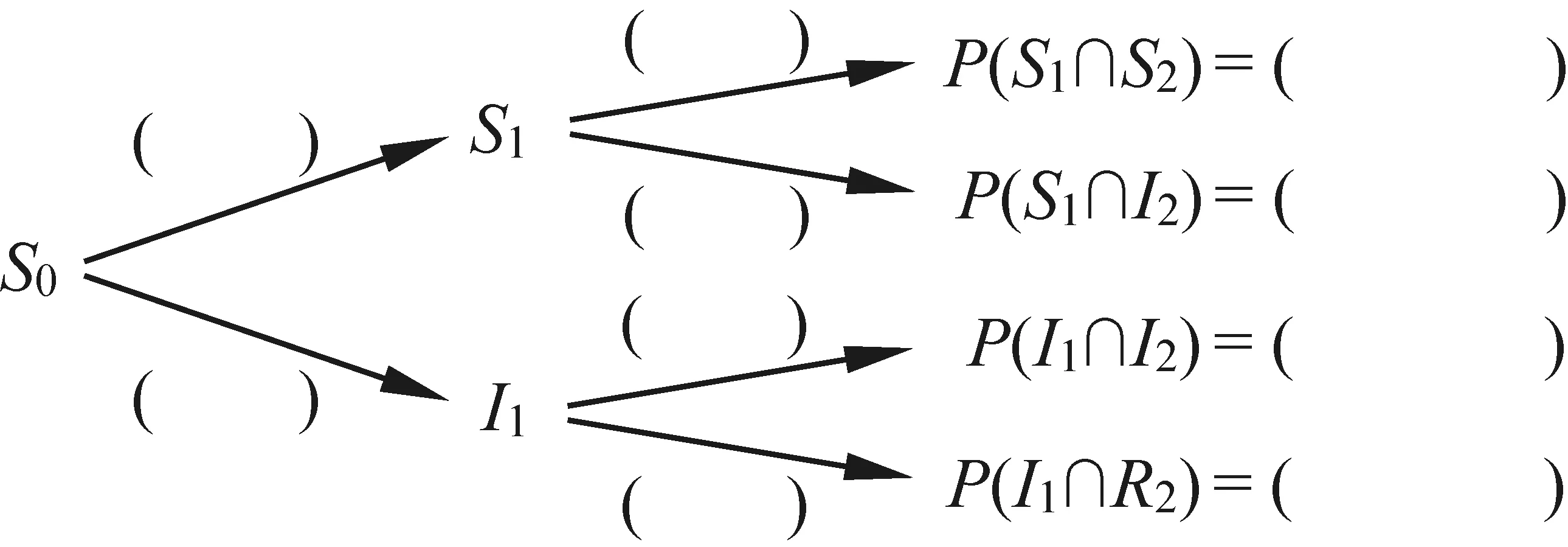
(2)对于任意自然数n,将事件Sn、In、Rn的概率分别记作un,vn,wn,即un=P(Sn),vn=P(In),wn=P(Rn).分别求数列{un}和数列{vn}的通项公式;
(3)对病毒传播的长期演变做出推断.
解(1)括弧中的数为发生的概率

(2)根据统计规律有
un+1=0.93un
①
vn+1=0.65vn+0.07un.
②
由①,得{un}是公比为0.93的等比数列,又因为u0=P(S0)=1,
所以,{un}的通项公式un=0.93n.
由②,得vn+1=0.65vn+0.07un
=0.65vn+0.07×0.93n,
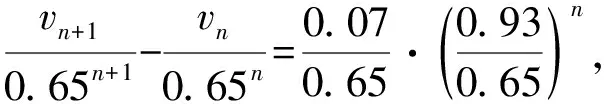
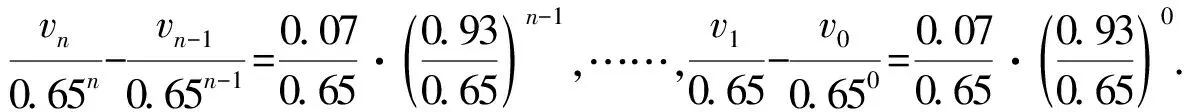
以上各式左右分别相加,注意v0=0,得
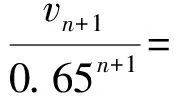
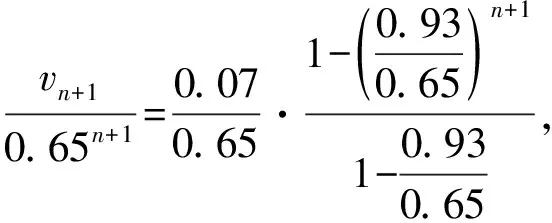
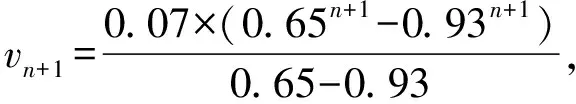
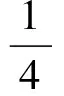
所以,{vn}的通项公式为
(3)因为人群只可能是S、M、I三种类型,所以un+vn+wn=1.
又因为数列{un}是公比为0.93的等比数列,当n充分大以后,un趋近于0;数列{vn}是公比都小于1的两个等比数列的差,因此当n充分大以后,vn趋近于0.
于是,数列{wn}趋近于1.因此,从长远来看,所有人都可以对病毒免疫.

