四开关Buck-Boost变换器同步双载波单模式控制策略
魏 青, 刘宝泉, 杨 振
(陕西科技大学 电气与控制工程学院, 陕西 西安 710021)
0 引言
近年来,电力电子技术快速发展,尤其是DC/DC变换器的发展和应用取得了长足进步.因为DC/DC变换器具有效率高、损耗少、可靠性高等优点,它的应用涉及到通信电源[1-3]、光伏发电[4-6]、计算机、家用设备和工业等各个领域.本文所介绍的是四开关Buck-Boost变换器(FSBB),它可以实现从输入到输出同相的宽范围升降压变换[7,8],为实际应用提供了更多的可能和便捷,这也意味着更复杂的控制和切换过程.
针对FSBB的传统控制策略主要有两模式控制策略[9-11]和三模式控制策略[12,13].文献[9]提出两模式控制下其实只有两个开关管在同时工作,开关损耗大幅降低,电感电流脉动大幅度减小,电感电流有效值减小,从而减小变换器的导通损耗.但两模式控制存在以下缺点:当输入电压与输出电压很接近时,FSBB将会在两个模式下来回转换,大大降低效率,影响电路的稳定性.为了解决这个问题,文献[10]中提出了滞环控制,但当输入电压处于滞环内时,输出电压无法稳定的达到设定值.
文献[11]提出了FSBB 三模式双频两沿精确调节控制策略.该控制策略下48 V输入时变换器的效率可达 97.8%,大幅度减小了开关损耗,进一步提高了升降压模式变换器的效率.但该控制策略存在以下缺点:该模式下FSBB工作在两种频率下,增加了驱动电路的复杂程度,三种模式间也难以实现平滑切换.有学者提出FSBB三种模式控制的软开关实现方式[14-17],三种工作模式对应三种频率变化关系,存在不同频率间切换的不稳定问题.还有学者提出了混合控制模式[18],但实现方法较为困难.
本文提出了一种同步双载波单模式控制策略,使得该拓扑可以在整个调压范围内实现平滑的切换,并且只存在一种工作模式.
1 四开关Buck-Boost变换器分析
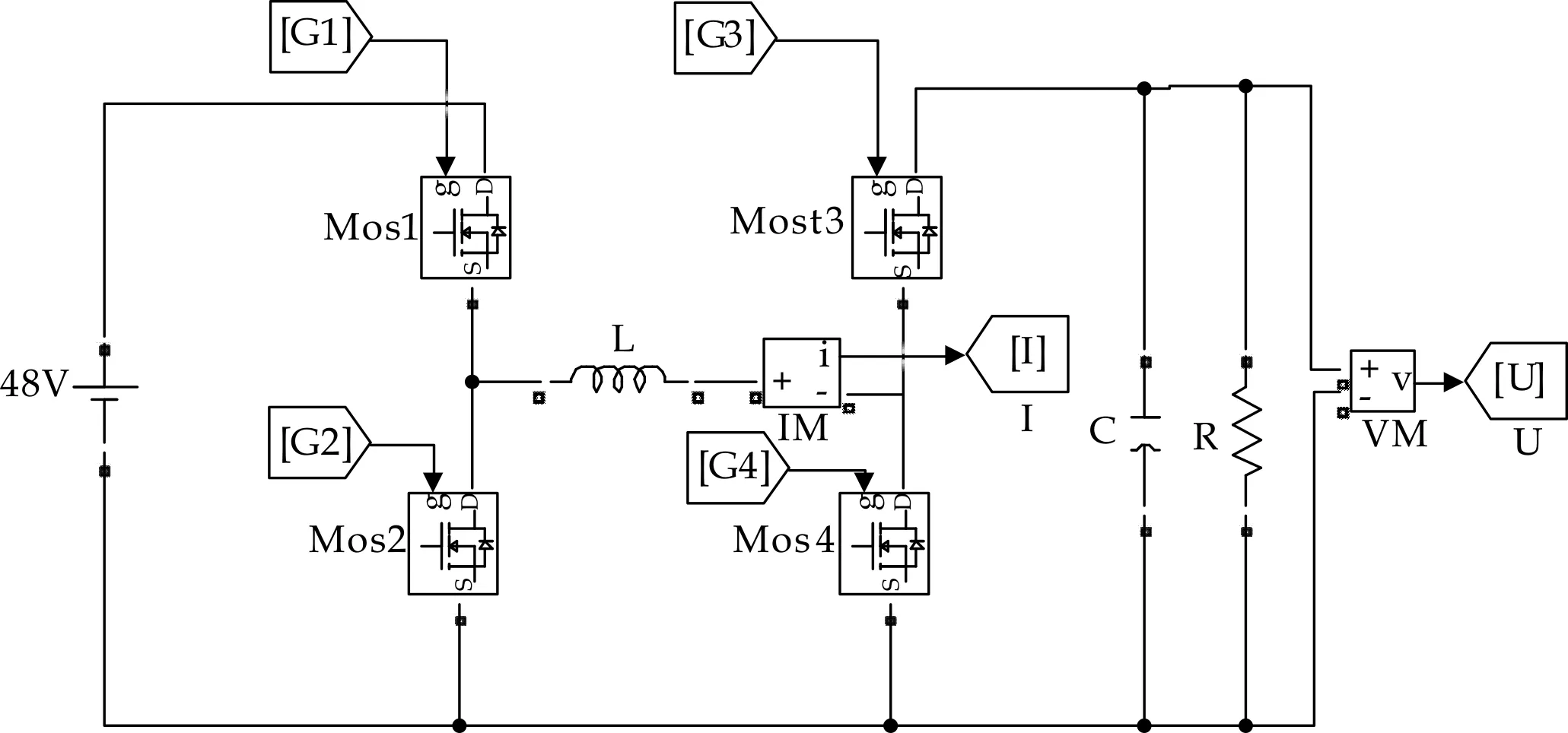
四开关Buck-Boost变换器的电路结构如图1所示.该电路可以实现从输入到输出同相的升降压变换,即可以实现从宽范围输入电压到固定输出电压,也可以实现从固定输入电压到宽范围输出电压.
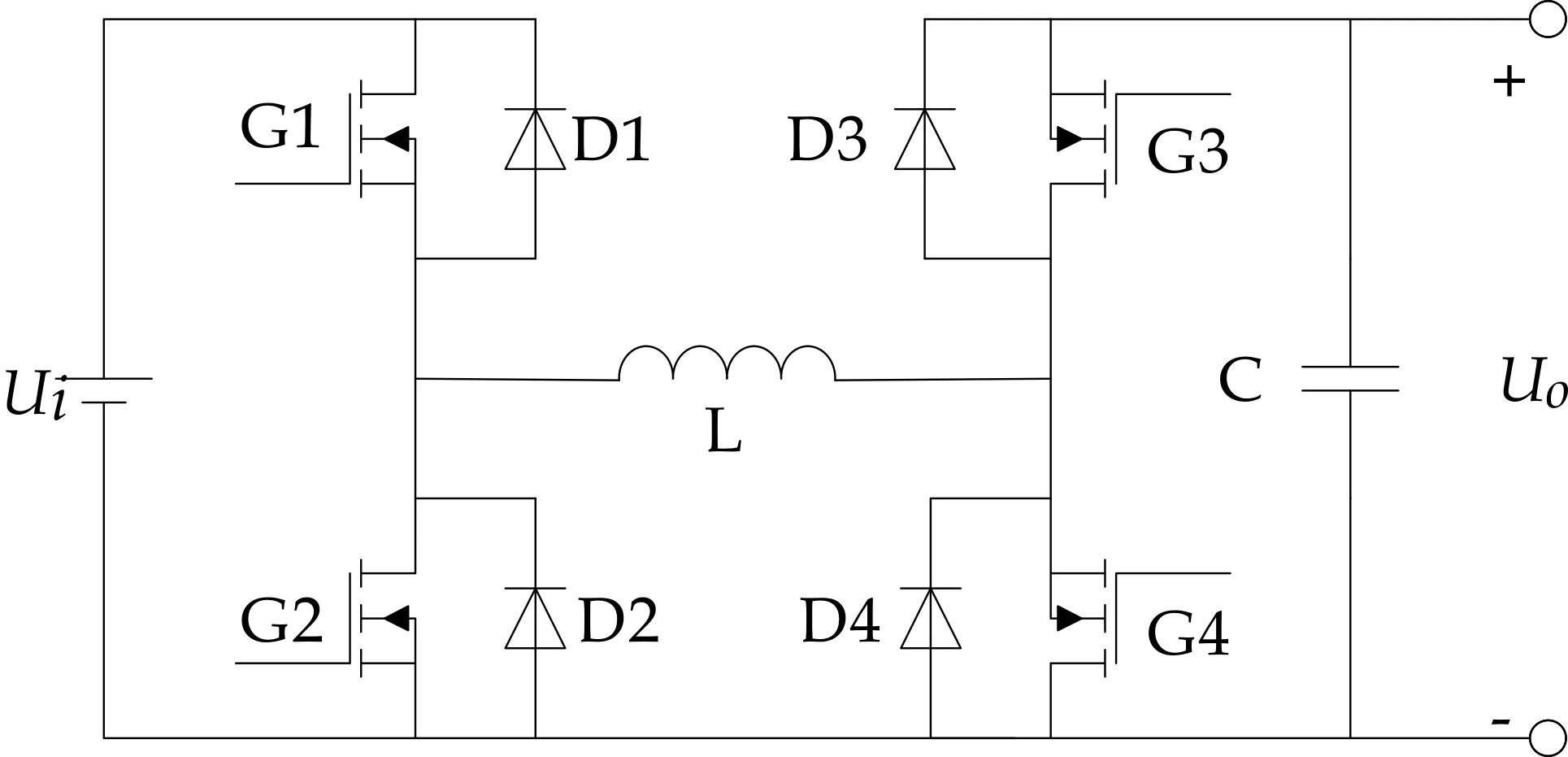
图1 四开关Buck-Boost变换器的电路结构
该电路可以看作由两个单元组成,开关管G1、G2组成Buck单元,G1、G2总是反向导通,G1为其控制管,假设其占空比为d1;开关管G3、G4组成Boost单元,G3、G4总是反向导通,G4为其控制管,假设其占空比为d2.
FSBB的四个开关管可以组成四种工作模态,分别为A、B、C、D模态,如图2所示.
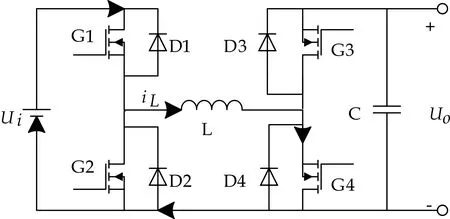
(a)工作模态A

(b)工作模态B

(c)工作模态C
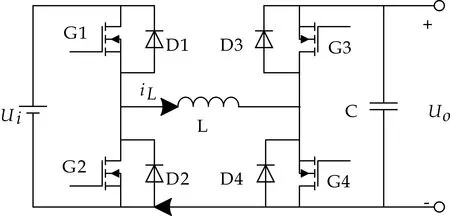
(d)工作模态D图2 FSBB的四种工作模态
工作模态A:是Boost电路的一种状态,该状态下开关管G1、G4导通,G2、G3关断,形成Ui-G1-L-G4通路.假设这一状态持续时长为To1,这一阶段电感电流连续上升,电感电流变化量为Δi1.其电感电流与输入电压的关系为:
(1)
工作模态B:即是Buck电路的一种开关状态,又是Boost电路的一种开关状态.该状态下开关管G1、G3导通,G2、G4关断,形成Ui-G1-L-G3-Uo通路.假设这一状态持续时长为To2,这一阶段电感电流变化量为Δi2,其电感电流与输入输出电压的关系为:
(2)
工作模态C:是Buck电路的一种状态.该状态下开关管G2、G3导通,G1、G4关断,形成G2-L-G3-Uo通路.假设这一状态持续时长为To3,这一阶段电感电流连续下降,电感电流变化量为Δi3,其电感电流与输入输出电压的关系为:
(3)
工作模态D:该状态下开关管G2、G4导通,G1、G3关断,形成G2-L-G4通路.这一状态电感电压应力为0,电感电流变化量也为0.
对于这四种模态,A、B组合为Boost电路的两种开关状态;B、C组合为Buck电路的两种开关状态.四种模态可以进行不同的组合,通过调节不同模态的工作时间以实现输出电压的改变.
2 同步双载波单模式控制策略
2.1 同步双载波单模式控制策略
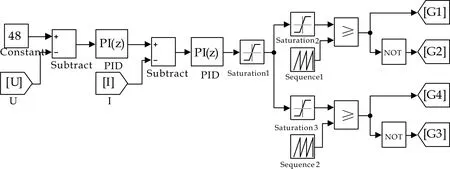
为解决两模式和三模式中遇到的问题,本文提出了同步双载波单模式控制策略.该模式下两个主开关管G1、G4始终是同时开通的,均在每个开关周期的开始时刻,且有两个载波序列,这两个载波序列具有不同的电压偏置,同时设置开关管的最大最小导通角,从而产生四个开关管的触发脉冲.在这种控制策略下,FSBB只存在一种工作模式.该模式下的开关管驱动电路如图3所示.
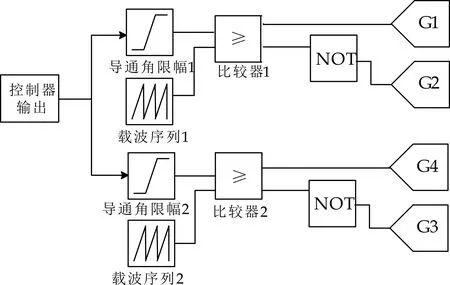
图3 FSBB开关控制电路
在图3中,控制器输出是指PI调节器的输出;导通角限幅1是对G1、G2的最大最小导通角进行限幅制,导通角限幅2是对G3、G4的最大最小导通角进行限幅制;比较器1、2的作用是将控制器输出与载波序列进行比较,产生四个开关管的脉冲序列;两个载波序列具有不同的直流偏置,本设计中载波序列相关参数设计如下:
第一路载波序列的幅值设置为[V1,V2],限幅值为[VBk-min,VBk-max];
第二路载波序列的幅值设置为[V2,V3],限幅值为[VBt-min,VBt-max].
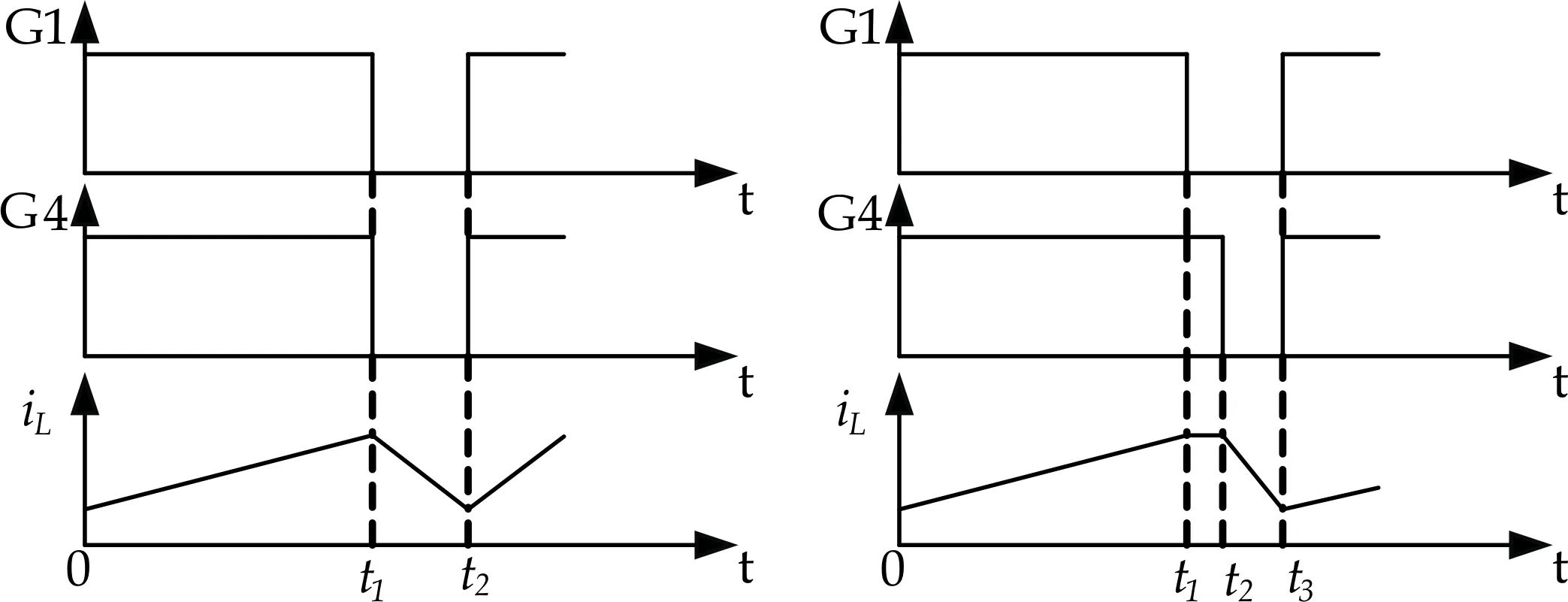
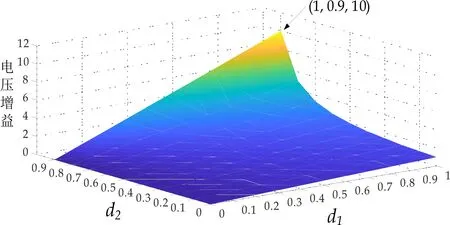
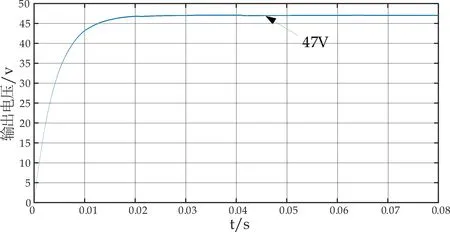
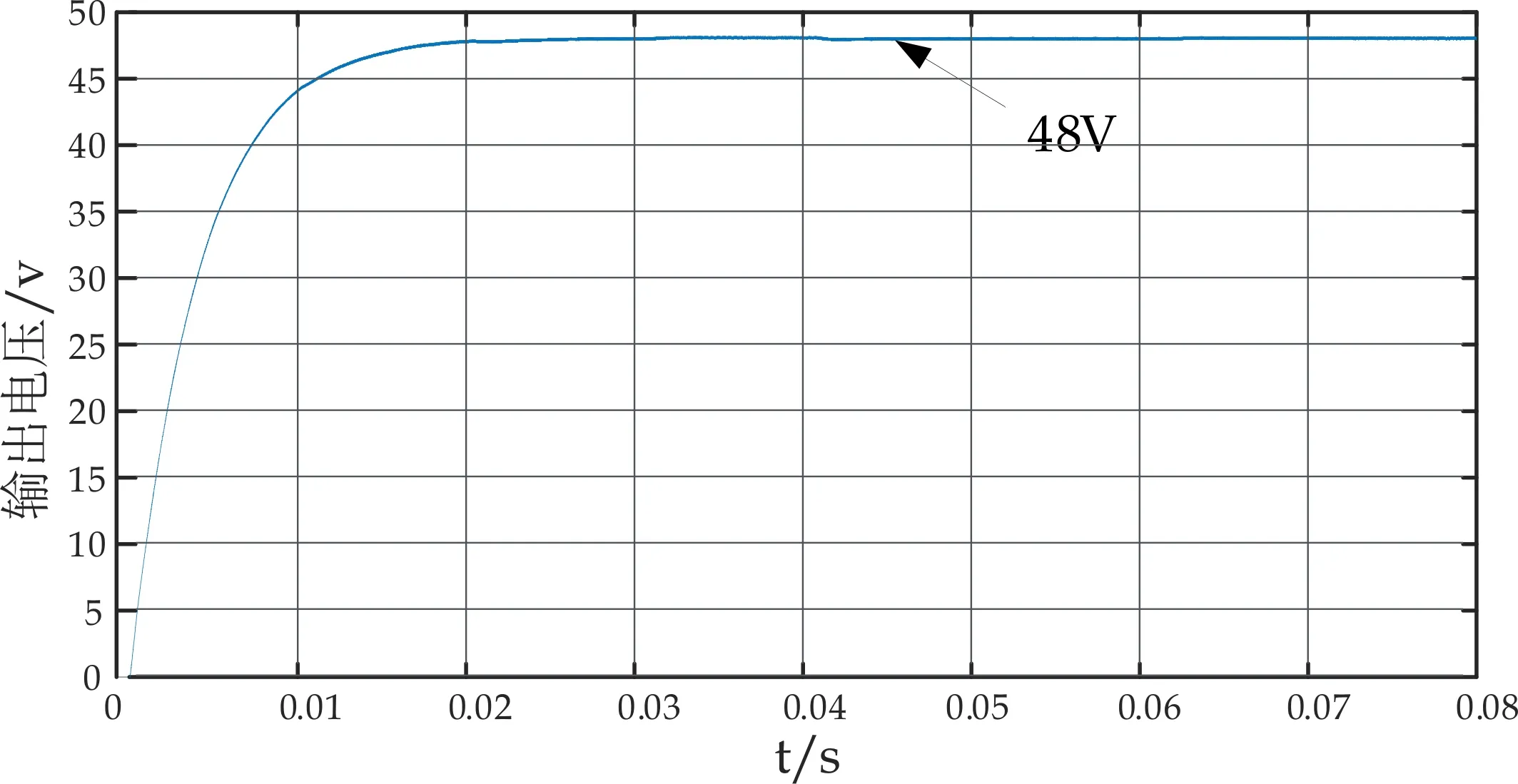
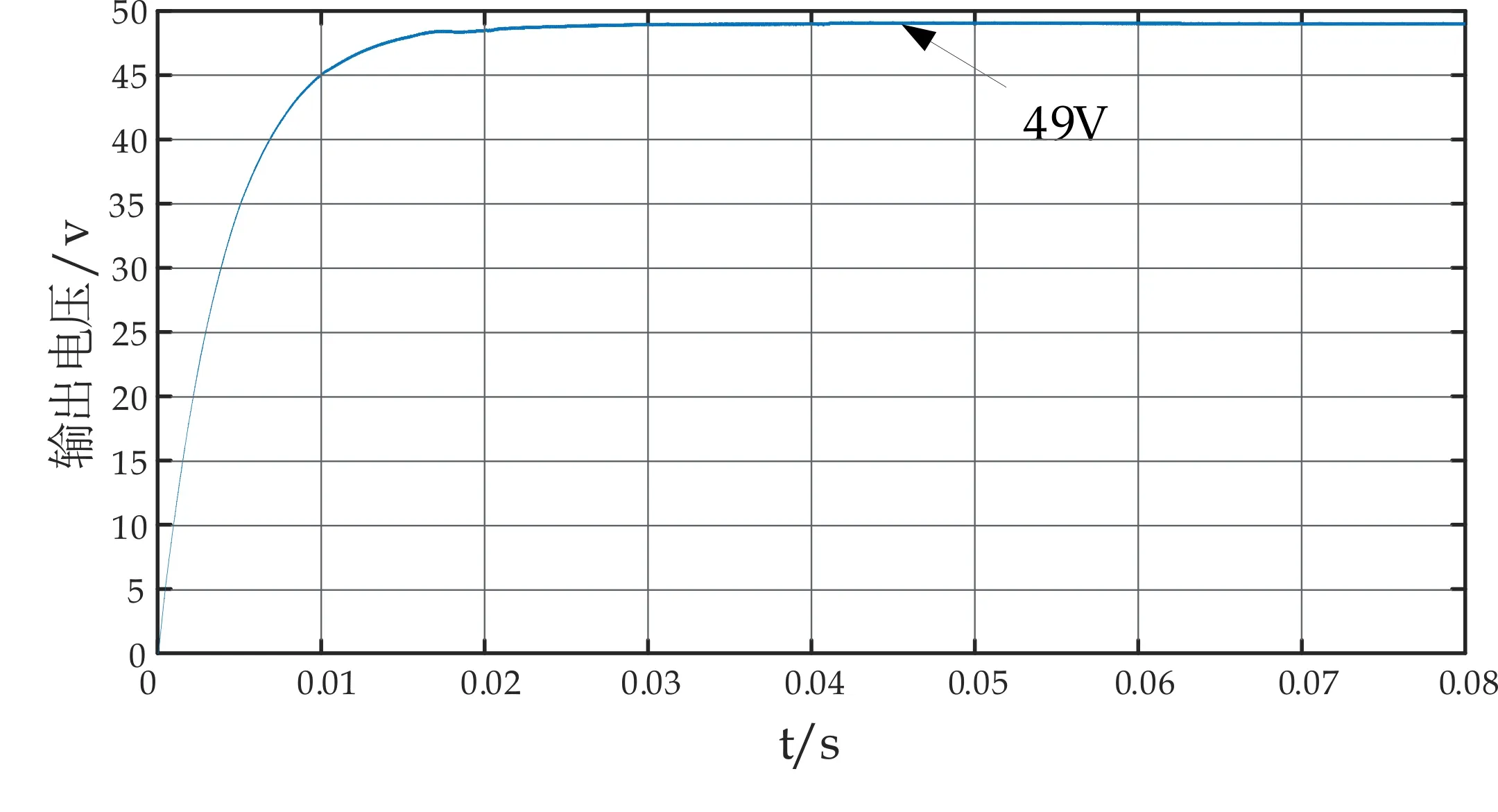
其中,V1 当控制器输出值在[VBk-min,VBk-max]范围内时,其与第一路载波序列比较后产生具有一定占空比的两路相反的控制脉冲G1、G2.由于第二路载波序列的幅值范围大于第一路的幅值范围,但其又有一定的限幅,所以此时经过与输入值的比较后,第二路产生始终维持在最小导通角DBt-min状态的触发脉冲G4和与其反向的脉冲G3. 当控制器输出值在[VBt-min,VBt-max]范围内时,与第二路载波序列比较后产生具有一定占空比的两路相反的控制脉冲G4、G3,由于第一路载波序列的幅值范围小于第二路的幅值范围,但其又有一定的限幅,所以此时经过与输入值的比较后,第一路载波序列产生始终维持在最大导通角DBk-max状态的触发脉冲G1和与其反向的脉冲G2. 该控制模式下,占空比的改变是连续的,因此,电路可以在不同的输出电压间进行平滑的切换,并且可以通过调节A、B、C、D四种模态的工作时间,即调节d1、d2的值实现不同的输出电压.不需要切换模式,不需要改变频率. 在前面分析了FSBB的开关管的四种工作模态,根据DBk-min、DBk-max、DBt-min、DBt-max的不同,每个周期内存在2~3种工作模态,以不同的工作顺序呈现.图4表示不同占空比下的时序图. (a)DBk-min≤d1 (c)DBt-min (e)d2=DBk-max (f)DBk-max 由图4可知,在同步双载波单模式控制策略下,FSBB的工作顺序有:A-B-C、A-D-C、A-C.图4的每种时序图对应的模态分析如表1所示. 表1 时序图对应模态分析 对于每种工作时序,都假设0~t1时间段内电感电流的变化量为Δi1,持续时长为To1;t1~t2时间段内电感电流的变化量为Δi2,持续时长为To2;t2~t3时间段内电感电流的变化量为Δi3,持续时长为To3,周期为T. 对于时序图4(a),Δi1=Δi3、To1=d1T、To3=T(1-DBt-min) . 对于时序图4(b),Δi1=Δi2、To1=Td1、To2=T(1-d1) . 对于时序图4(c),Δi1+Δi2=Δi3、To1=DBt-minT、To2=T(d1-DBt-min)、To3=T(1-d1). 以上三种情况分别代入公式(1)、(2)、(3)中,可得占空比与输入输出电压的关系式均为: (4) 对于时序图4(d),Δi1=Δi2+Δi3、To1=d2T、To2=T(DBk-max-d2)、To3=T(1-DBk-max). 对于时序图4(e),Δi1=Δi2、To1=Td2、To2=T(1-d2). 对于时序图4(f),Δi1=Δi3、To1=DBk-maxT、To2=T(d2-DBk-max)、To3=T(1-d2). 以上三种情况分别代入公式(1)、(2)、(3)中,可得占空比与输入输出电压的关系式均为: (5) 由以上分析可知,同步双载波单模式控制策略下占空比与输入输出电压的关系可以总结为: (6) FSBB的增益与占空比关系的曲面图如图5所示. 图5 FSBB增益曲面图 由式(6)可知,当d2为0时,电路工作在Buck状态,当d1为1时电路工作在Boost状态.由图5可直观地看出,当d1、d2为其他可能的值时,FSBB将工作在单模式下,因为占空比的改变是连续的,电路可以在不同的输出电压间进行平滑的切换,即通过调节A、B、C、D四种模态的工作时间,也就是通过调节d1、d2的值实现不同的输出电压. 当占空比在0~1范围内时,变换器的增益范围为0~10.可见该控制模式下可实现较宽范围的输出电压. 本文的相关设计指标为: (1)输入电压:48 V; (2)开关管工作频率:100 kHz; (3)功率:200 W. FSBB的双闭环仿真模型如图6所示. (a)主电路仿真图 (b)控制电路仿真图图6 FSBB的仿真模型 文章对FSBB进行了双闭环控制,图6(a)是FSBB主电路仿真图,图6(b)是FSBB的双闭环控制电路仿真图. 输入电压为48 V,输出电压为47 V、48 V、49 V时的输出电压波形分别如图7(a)、(b)、(c)所示. (a)47 V输出电压波形图 (b)48 V输出电压波形图 (c)49 V输出电压波形图图7 输出电压波形图 由图7可以看出,输出电压为47 V、48 V、49 V时的波形非常稳定,解决了两模式控制中输出电压靠近输入电压时,输出在两个模式下来回切换的问题,并且只有一种频率、一种工作模式和一个控制器.由此可见,同步双载波单一模式控制策略下,可以使输出电压在较宽范围内稳定平滑的输出. 对四开关Buck-Boost变换器提出了一种同步双载波单模式控制策略,可以在较宽范围内实现平滑稳定的改变输出电压,不需要增加变频电路,不需要模式切换,控制电路和驱动电路都相对简单.该控制策略通过具有不同直流偏置的两路载波序列,对其设置不同的限幅值,使开关管具有一定的初始和最大导通角,从而为四个开关管提供触发脉冲,实现同步双载波单模式控制策略.同时通过对FSBB的模态分析、驱动电路分析和时序分析,得到了输入输出电压与实际占空比的关系,分析结果表明通过调节A、B、C、D四种模态的工作时间,电路可以在不同的输出电压间进行平滑的切换,从而达到稳定的输出电压.最后对FSBB进行了双闭环仿真,结果表明FSBB在该控制策略下输出电压可以实现平滑的切换,证明该控制策略有效可行.2.2 时序分析



3 仿真验证
4 结论

