谐波分析在贵阳市降水预测中的应用
周 林,李 扬,彭科曼,罗乃兴
(贵州省贵阳市气象局,贵州 贵阳 550001)
1 引言
我国气候灾害发生率较高,因此短期气候预测一直是我国气象学家重点关注及研究的问题。而降水预测是短期气候预测的重要内容之一,其是制定防灾减灾对策的重要依据,并且对国家防御和减轻气象灾害具有重要贡献。对于降水这一长期时间序列,其包含月、季、年等多种时间尺度,也就是说它包含有各种复杂的波动,而谐波分析是用来识别和提取时间序列周期项的有效方法,根据谐波分析原理,任一时间序列可以看作是由一系列正弦波迭加而成。谐波分析方法在气象上有诸多应用,不仅可以对时间序列进行谐波分析研究其周期变化,另外还可用来分析空间场,将它用于空间高度场上,可以定量分析出长波、超长波的振幅、方差贡献百分比以及槽(脊)位置随时间的变化,用于天气分析和预报[1-5]。
由于谐波分析是识别和提取时间序列周期项的有效统计分析方法[6-8],因此谐波分析方法在短期气候预测中有较多的应用。例如谐波分析可用于气象要素时间序列的滤波处理,周成霞等[9]采用谐波分析将我国冬、夏季平均气温和降水序列分解为慢、快变分量(其对应年代际、年际变化分量),并且分析慢、快变分量序列中气温和降水间的局地同期相关联系,为揭示年代际、年际变化对我国气候异常特征的影响提供了重要依据;段明铿等[10]利用谐波分析研究了我国夏季东部降水异常的年际和年代际成因。另外谐波分析在气象要素气候趋势预测分析中有较多运用[5,7],例如邢纪元[3]利用谐波分析对泰安年、月降水进行了分析和预报,收到了良好预测效果;王斌生等[11]通过对气候要素旱涝的谐波分析建立预测模型,并应用于气候旱涝预测中,成功预测了降水旱涝年,效果良好;李安国[12]使用长达几十年的连续时间序列资料,消除“常用周期”后进行谐波拟合,并将其应用于气候趋势预测中,预测效果较为满意;吕新等[13]应用谐波分析方法建立了拟合模型,并对石河子未来年份的春季晚霜进行了预测;迟道才等[14]建立了基于谐波分析的降水预测模型,结果表明谐波分析模型具有高的精度和稳定性。综上所述,谐波分析在短期气候预测中具有较好的预测效果,为此本文将谐波分析应用于贵阳市旱涝预测中并对其预测效果进行检验。
利用贵阳市7个气象观测站多年降水资料,在统计分析的基础上应用谐波分析方法,建立贵阳市旱涝预测模型,并在已有降水历史资料的基础上,利用预测模型计算预测年份降水距平预测值,并与实际降水距平值进行比较,检验其预测效果的好坏。
2 资料和方法
2.1 资料
选取1963—2017年共55 a的贵阳市7个常规气象观测站(贵阳、乌当、清镇、息烽、开阳、修文、花溪)的逐日降水资料,根据逐日降水资料计算出每个气象观测站的历年降水量。将贵阳市1963—2012年的历年降水距平序列作为样本值,利用谐波分析,建立降水预测模型,然后对2013—2017年的年降水异常值进行预测,并对其预报效果进行检验。文中距平值均为原始值与气候均值(1981—2010年)的差值。
2.2 主要方法
2.2.1 谐波分析的基本原理[6-7]谐波分析是用来识别和提取时间序列周期项的方法,目的是从不规则的振动曲线中分离出若干振幅和位相不同的简谐波,以便逐个研究其统计规律与特征。设有一个已知周期T的气象时间序列,若以整个周期内n个等距观测值,y1、y2、…、yn来代表,可以发现其观测值随时间的演变曲线并不是光滑的,在基本周期T上,还迭加着许多其它的周期振动或随机扰动。
2.2.2 谐波分析的数学模式[7]根据傅里叶级数理论,一个以基本周期T为区间的函数f(t),若满足一定的条件总可以表示成一系列频率成倍增加的谐波之和,即
(1)

将(1)式变换为下列形式
(2)
(2)式即为谐波分析的一般模型,其中a0,ak=cksinφk,bk=ckcosφk称为傅里叶系数,其中:
(3)
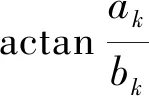
根据最小二乘法和三角级数的正交性,对于离散的时间序列y1、y2、…、yn,按照周期区间(0,T)上的n个等间距时刻估计系数ak和bk,则傅里叶系数的计算式为
(4)
由于序列的长度n有限,实际上只能取有限个正弦波来逼近序列{yt} ,一般来说所取的谐波数最多只能为n/2,因此(2)式等号右边只能为有限项。即
(5)
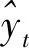

波数k12…K周期Tkn/1n/2…n/K频率ωkω2ω…Kω

2.2.3 谐波分析的显著性检验 利用正交性可以证明原序列{yt}的总方差和各谐波分量的振幅ck有如下关系
(6)
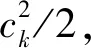
(7)

3 计算结果及预报检验
3.1 贵阳地区降水的年际和年代际变化特征
根据贵阳地区1963—2017年的降水资料序列,通过计算得出贵阳地区1981—2010年近30 a的气候平均年降水量为1 107.05 mm。根据一元线性回归方程[15],近55 a贵阳地区年降水量呈递减趋势,递减率为-13 mm/10 a,但未通过显著性检验,表明贵阳地区年降水变化趋势并不显著,但是年际间波动振幅较大(图1)。年降水量最多的年份是1977年,其年降水量为1 491.56 mm,降水距平百分率为34%(图1),其降水量是气候平均值的1.3倍;而2011年的年降水量最少,只有794.07 mm,降水量较常年偏少近三成。从图1和表1可以发现贵阳地区年降水在某些年为明显的极端旱涝年,其中1977、1996和2015年为降水极大值年,而降水极小值年出现在1966、1981和2011年。

图1 1963—2017年贵阳地区年降水距平百分率及其7 a滑动平均值的年际变化Fig.1 The percentage of annual precipitation anomaly and its seven-year sliding average in Guiyang region from 1963 to 2017
表1为贵阳地区各年代的年降水量统计结果,可以发现20世纪80年代和21世纪00年代的年平均降水量均低于气候平均年降水量,再结合图1给出的7 a滑动平均曲线,可见贵阳地区年降水量具有显著的年代际变化,其中20世纪80年代和21世纪00年代降水相对偏少;20世纪60年代到70年代、20世纪90年代和21世纪10年代降水相对偏多。这与图2的Mann-Kendall突变检验[15]是一致的,图中UF和UB两条曲线在1980年相交,表明贵阳地区年降水在1980年左右发生突变,降水由之前的偏多转为偏少。

表1 1963—2017年贵阳地区各个年代的降水量Tab.1 Precipitation in different periods in Guiyang region for the period 1963—2017

图2 1963—2017年贵阳地区年降水量Mann-Kendall突变检验序列,短虚线表示5%的显著性检验水平Fig.2 Mann-Kendall test of annual precipitation in Guiyang region for the period 1963—2017, the short dashed line indicates the 5% significant level of the Mann-Kendall test
3.2 谐波分析在贵阳地区降水上的模拟应用
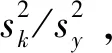

表2 贵阳地区1963—2012年年降水距平的谐波分析参数Tab.2 Harmonic analysis parameters of precipitation anomaly in Guiyang region from 1963 to 2012
注:*表示通过信度0.05的显著性检验
查F分布表可知,在25个谐波中只有K=2、7、17、20、23等5个波是通过信度α=0.05显著性水平的F检验,这5个波占总方差的比重是53.80%,其分别对应周期是25 a、7.14 a、2.94 a、2.5 a、2.17 a(表2),可见贵阳地区的年降水存在显著的25 a和7 a左右的年代际周期振荡,另外还存在明显的准2~3 a的年际周期振荡。根据前文公式(5),运用这5个显著的谐波对贵阳地区年降水量距平序列进行谐波拟合,其拟合方程为:
(8)
利用(8)式对贵阳地区1963—2012年的年降水距平序列进行拟合,并预测2013—2017年的年降水距平值,其计算结果见表3和图3。
从表3和图3可以发现,运用谐波分析得到的降水预测模型对贵阳地区的年降水距平进行拟合及预报中,降水距平拟合值和实况值的变化趋势基本一致,其中拟合得到的峰值和谷值与实况也比较符合,但是其对谷值的拟合效果明显优于对峰值的拟合效果(表3);另外本模型对一些突出的旱涝年也能较好的模拟和预测出来,如1966年和1981年降水异常偏少是明显的旱年,其都模拟正确;另外2015年是涝年,预测正确(图3)。
从2013—2017年的年降水距平预测值与实况值的比较可以看出(图3),模型预测的降水偏多年和偏少年与实况完全吻合,其预报的降水变化趋势完全正确。应用该预测方程预测2018年的降水变化情况,计算结果表明,2018年贵阳地区年降水量较常年略偏少,出现大旱的可能性不大。

表3 1963—2012年贵阳地区降水实况值与模拟值的验证情况Tab.3 The verification of actual value and simulation value of precipitation in Guiyang region from 1963 to 2012

图3 贵阳地区1963—2012年降水距平值和拟合值以及2013—2017年的降水距平预测值(红线)Fig.3 Precipitation anomaly value and fitting value from 1963 to 2012 and precipitation anomaly prediction value in 2013—2017 (red line) in Guiyang region
4 结论
①通过对贵阳地区的年降水距平序列统计分析发现,贵阳地区的年降水存在明显的年际和年代际变化特征。贵阳地区近55 a的年降水量呈递减趋势,但变化趋势不显著,年降水量最大值为1 491.56 mm(1977年),年降水量最小值为794.07 mm(2011年);20世纪80年代和21世纪00年代降水相对偏少,20世纪60—70年代、90年代和21世纪10年代降水相对偏多,并且利用Mann-Kendall突变检验发现贵阳地区年降水量在1980年发生年代际突变。
②利用谐波分析发现,贵阳地区年降水量在年际变化上存在明显的2~3 a的年际周期振荡,而在年代际变化上存在准25 a和7 a左右的年代际周期振荡。
③利用谐波分析得到的降水预测模型对贵阳地区年降水距平进行拟合及预测后,与实况值对比分析表明,降水距平拟合值和预测值与实况值的变化趋势基本一致,并且该预测模型对一些突出的旱涝年也能较好的模拟和预测出来。该预测模型方法简单,可操作性强,并且预测结果良好,可在实际业务中推广应用,其在贵阳市降水短期预测中具有一定参考价值。

