对冲基金分布复制模型的协方差估计与算法实现

孙慧萍， 王美清， 洪倩颖

(福州大学数学与计算机科学学院， 福建 福州 350108)

0 引言

对冲基金充分利用金融衍生品的杠杆效应， 追求高收益， 是众多投资者喜爱的投资模式[1]. 近年来, 随着母基金(fund of funds)的出现， 对冲基金复制策略[2]成为均值-方差模型的一类有效补充， 受到了基金业界人士的关注. 分布复制法是对冲基金复制技术之一， 文献[3]于2003年首次尝试这一复制方法. 文献[4]应用基于 copula的动态复制策略， 选择传统金融资产的期货合约作为复制工具提出基于投资者现有投资组合的依赖结构的分布复制法. 在此基础上， 文献[5]提出改进， 在不完全市场中利用期权的对冲策略方法构造动态投资组合. 文献[6]在Papageorgiou模型的基础上， 提出了满足初始投入最小的动态投资组合策略的分布复制法.

金融回报的协方差矩阵估计在资产配置的过程中具有十分重要的位置. 经典的估计方法有基于因子模型[7]、 基于收缩模型[8]、 指数移动加权平均等估计方法. 而随着近些年高频交易的深入研究和发展， 协方差矩阵估计也迎来了新的挑战. 文献[9]构造了一种方便计算的综合协方差矩阵的非线性收缩估计量. 文献[10]提出了一种基于金融回报是多元时间序列的协方差矩阵的估计方法， 针对非同步交易以及微观结构噪音污染， 文献[11]提出了一个不假设资产综合协方差矩阵具有特殊结构的非参数特征值正则化的综合协方差矩阵估计量(nonparametrically eigenvalue-regularized integrated covariance matrix estimator， NERIVE).

本研究主要讨论在Takahashi模型[6]中波动率矩阵的计算过程中, 如何确定协方差矩阵. 采用基于因子模型的估计方法和基于收缩模型的估计方法来替代指数移动加权平均法. 另外， 考虑到金融数据具有噪声， 本研究对市场数据进行了去噪预处理[12].

1 Takahashi模型

(1)

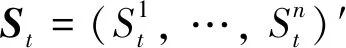
(2)

若σt可逆， 那么存在唯一的风险市场价格θt和唯一的状态价格密度过程Ht

(3)

(4)

文献[13]提出当末端资产分配的权重是关于状态价格密度的减函数时，x=E[HTX]将得到最小值， 其中E为期望函数. 因此给定末端回报的分布函数， 可以通过复制该分布使得初始投入最小， 从而达到收益最大.

假设ξ是具有给定目标分布函数Fξ的随机变量；Lt是如下定义的随机变量：

(5)

FLT是LT的分布函数， 且FLT可逆. Takahashi模型[6]证明了当末端回报随机变量X定义如下时， 与ξ同分布：

(6)

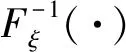
当r、μ和σ是关于时间t的确定函数时， 参考文献[6]给出了如下定理.

定理1假设r、μ和σ是关于时间t的确定函数， 则在完全市场中， 公式(4)～(5)给出的末端回报f(LT)对应生成的动态投资组合可以表示为：

(7)

2 分布复制投资组合模型计算

式(7)给出了由分布复制法确定的动态投资组合计算公式. 实际计算时，需要确定随机向量θt，Ht，LT， 以及函数f(·). 风险市场价格θt与状态价格密度过程Ht可以通过式(3)计算获得，Lt与f(·)分别由式(5)与式(6)给出， 其中Fξ为待复制策略分布，F(LT )与Ht相关. 所以动态投资组合的计算最终归结为rt，μt与σt三个参数的计算. 其中无风险利率rt可以直接从市场中获得， 因此只要再确定漂移率μt与波动率σt即可.

2.1 样本协方差矩阵

定义风险资产i在时刻t(d)的日对数收益率：

(8)

(9)

2.2 指数加权移动平均

假设{xt}是一个时间序列, 指数加权移动平均方法(exponentially weighted moving average， EWMA)通过计算一个平均值序列{St}来分析时间序列数据的特点. 如果时间窗口为m, 则计算公式为：

(11)

其中, 0<λ≤1表示衰退系数. 衰退系数越小， 则靠近t时刻的收益值权重越大.

2.3 波动率矩阵与漂移率

(12)

(13)

3 协方差矩阵估计

对协方差矩阵进行估计， 一方面可以减小噪声对波动率矩阵的影响， 另一方面可以避免由矩阵奇异对求逆造成的影响.

参考文献[6]直接采用指数加权移动平均法来估计协方差矩阵：

(14)

(15)

然而指数移动加权平均法完全依赖样本数据， 且如果样本过多， 则计算量大. 本研究采用基于因子模型的估计方法和基于收缩模型的估计方法来替代指数移动加权平均法. 从而减少数据的维数， 并降低估计误差. 基于收缩模型的估计方法， 将用户预定义的一个矩阵和利用式(10)计算的协方差做线性组合， 以减少样本协方差的估计误差.

3.1 基于因子模型估计

因子模型可以通过给协方差矩阵定义一定的结构， 从而减少数据维数， 通常可以分为单因子模型与多因子模型.为了简便起见， 本研究仅考虑单因子的市场模型：

(16)

(17)

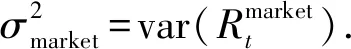
(18)

其中:T为风险资产回报Rt的时间长度.

3.2 基于收缩模型估计

虽然样本协方差矩阵Σt是协方差的一个无偏估计， 但是当风险资产个数n较大时， 经常是病态的. 因此基于收缩模型的估计方法考虑一个用户预先给定， 且一般是良态的协方差的估计值M为初始值， 通过与样本协方差线性组合向协方差矩阵收缩：

(19)

其中:ρ表示收缩强度.

参考文献[8]证明了在资产回报Rt是正态独立同分布的假设下， 式(19)及其中的收缩强度ρ可以用如下公式计算：

(20)

其中:n为风险资产的个数;T为Rt的时间长度;Idn为n维单位矩阵; tr表示矩阵的迹.

4 算法实现

4.1 数据预处理

金融数据通常包含噪声， 具有复杂的不规则结构， 因此， 在进行金融数据挖掘之前， 需要进行去噪处理来清洗数据. 以获得更加准确的结果. 本研究使用修剪过的均值滤波器[12]， 这个滤波器本质上是一个均值滤波器，其不同之处在于， 先对数据Xt的一个滤波窗口大小为N的子集进行排序， 然后对得到的顺序统计量R(1), …,R(N)进行修剪， 去掉r个最小的和s个最大的顺序统计量， 则可以得到(r,s)-修剪过的均值滤波器：

(21)

4.2 算法

基于分布复制的动态投资组合算法具体描述如下:

4) 将风险市场价格θt代入式(3)， 得到状态价格密度过程Ht； 代入式(5)， 可以得到Lt.

5) 将θt，Ht，Lt， 代入式(7)可以得到φt， 式(7)中的f(LT)可以根据式(6)求得， 在本研究中，FLT与Fξ都假设是正态分布.

6) 将φt与波动率矩阵σt代入式(11)， 可以得到动态投资组合πt.

5 实证与分析

本研究使用道琼斯瑞士信贷对冲基金指数作为对冲基金的表现， 可以从其主页上下载每月的数据. 同时， 本研究使用美元兑日元汇率(USD/JPY)和日元黄金(GOLD)作为复制对冲基金指数的工具， 选择S&P 500期货合约作为基于因子模型估计的市场指标.

5.1 误差分析指标

5.2 实验结果对比与分析

首先， 本研究在未经去噪处理和经过去噪处理的情况下， 分别对比了不同协方差矩阵估计方法下， 2006年1月3日到2007年1月3日目标资产与复制策略之间的均方误差以及对数收益率的分布情况， 如表1～2所示. 其中， 由于目标资产只有月度数据， 因此根据其均值方差以及Black-Shores模型， 给出其可能的资产增长情况. 而去噪处理过程中， 本研究使用的滤波窗口N=7， 在每个窗口内， 去掉1个最小的和1个最大的顺序统计量.

表1 未经去噪处理目标资产与不同方差估计模型下复制策略比较

表2 去噪处理后目标资产与不同方差估计模型下复制策略比较

6 结论

本研究基于Takahashi的初始投入最小的分布复制模型， 研究了对资产价格进行去噪处理， 以及对对数收益率的协方差矩阵进行不同的估计， 所对应的复制策略的资产分布以及与对应目标资产的比较. 经过实证分析可以发现， 经过去噪处理后的复制策略， 一般所含的风险更小. 在三种不同的协方差矩阵估计方法中， 由于复制的资产个数并不多， 因此因子模型并没有体现出在降维方面优势， 则对应得到的复制策略对比使用指数加权移动平均估计协方差的复制策略并没有更高单位风险价格； 而运用收缩的协方差矩阵估计， 所获得的复制策略的单位风险价格明显高于使用指数加权移动平均估计协方差的复制策略.