基于BP神经网络原理的人造岩心配比设计模型*

秦正山，罗 沛，张文昌，刘先山，谢 晶，周建良

（1.重庆科技学院石油与天然气工程学院，重庆 401331；2.中原油田石油工程技术研究院，河南 濮阳 457000）

0 前言

在石油开发研究领域，利用天然岩心进行室内物理模拟实验是石油开发技术人员进行理论研究的重要手段［1］。随着多年来对天然岩心的使用，可用的天然岩心数量逐渐减少。各大油田原始取心已难以满足后期石油开发研究的需要；取心成本较高，取心的完整性受到工艺技术、地层条件的制约。利用人造岩心模拟已知物性参数的原位地层来替代天然岩心，已成为石油开发室内研究的一种趋势［2］。

人造岩心通常有3种，即石英砂填砂管、石英砂环氧树脂胶结岩心、石英砂磷酸铝胶结岩心。其中应用最广泛的石英砂环氧树脂胶结岩心是通过粒度调节控制渗透率、孔喉比；通过调节胶结物加量和压制压力控制孔隙度［3］。但人造岩心物性参数的影响因素是多元的，孔、渗参数、粒度中值受到如粒径配比、胶结剂用量、压制压力、黏土含量、碎屑含量等因素的共同影响。按照传统人造岩心的孔渗参数控制图版所制的岩心物性参数模拟误差大，模拟范围窄，缺乏精确定量数据支持，一般需要制作多块岩心进行筛选。砂砾用量调整后导致孔隙度、渗透率、粒度中值等均发生变化，若只进行单因素调整来制备符合物性要求的岩心，显然存在所制岩心误差较大及多目标参数难以同时控制的问题。

以数据为载体，建立物性参数与数据化后影响因素的函数关系，对于解释多因素影响条件下难以用具体的函数表达式反映目标参数与影响因素之间的相关关系具有独到之处。国内在人造岩心制备领域，基于实验数据和数学算法的人造岩心制备研究方面几乎空白。笔者通过综合、全面的考虑人造岩心物性参数的主要影响因素，基于实验数据和BP神经网络原理［4］，建立人造岩心不同粒径砂配比设计模型，比较了根据该模型制备的人造岩心物性参数与期望物性参数的误差。

1 实验部分

1.1 材料与仪器

石英砂，安徽凤阳胜利石英砂厂；磷酸，工业级，上海阿拉丁生化科技股份有限公司；氢氧化铝，分析纯，天津致远化学试剂有限公司；蒸馏水。

选用江苏拓创科研仪器有限公司的RZYX-2型人造岩心制作装置，岩心模具用优质不锈钢材料制成，设计压力为40 MPa；压制岩心长度25数300 mm，压制岩心直径为25、28 mm。

1.2 实验方法

1.2.1 实验设计

（1）将人造岩心的物性参数作为岩心仿真度的目标参数，包括孔隙度、渗透率、粒度中值；（2）综合全面考虑人造岩心的物性参数可能存在的影响因素，建立人造岩心配比设计正交方案，根据方案制备人造岩心并测定其物性参数；（3）分析预考虑影响因素与物性参数的关系；（4）采用灰色关联法，分别计算各影响因素与物性参数的关联度，明确岩心孔隙度、渗透率、粒度中值的主要控制参数，分析和判断预考虑影响因素的合理性；（5）基于影响因素分析结果、实验数据及BP神经网络原理，建立人造岩心配比设计数学模型，检验模型的稳定性和误差范围，直到满足误差要求；（6）设定10块岩心期望物性参数值，由模型计算不同粒径石英砂和胶结剂加量，并以此为据制备岩心，对比物性参数测试值与期望值，检验误差。

1.2.2 标准实验岩心的制备

将磷酸、氢氧化铝、水以质量比100∶20∶30混合均匀，快速加温至沸腾并间歇搅拌，沸腾持续至氢氧化铝粉末完全溶解后停火，自然冷却制得磷酸铝胶结剂。按0.224数 0.45 mm（70数 40 目）、0.154数0.28 mm（100数 60 目）、0.074数 0.18 mm（200数 80目）3 种粒度范围筛选精制石英砂。岩心制作时仅用石英砂，未添加黏土、碎屑等其他矿物。在不同粒径的精制石英砂中加入磷酸铝胶结剂，制备标准岩心。

1.2.3 实验方案

制定岩心配比设计正交方案（表1），制作21 块实验岩心，制备工序可参考文献［5-7］。

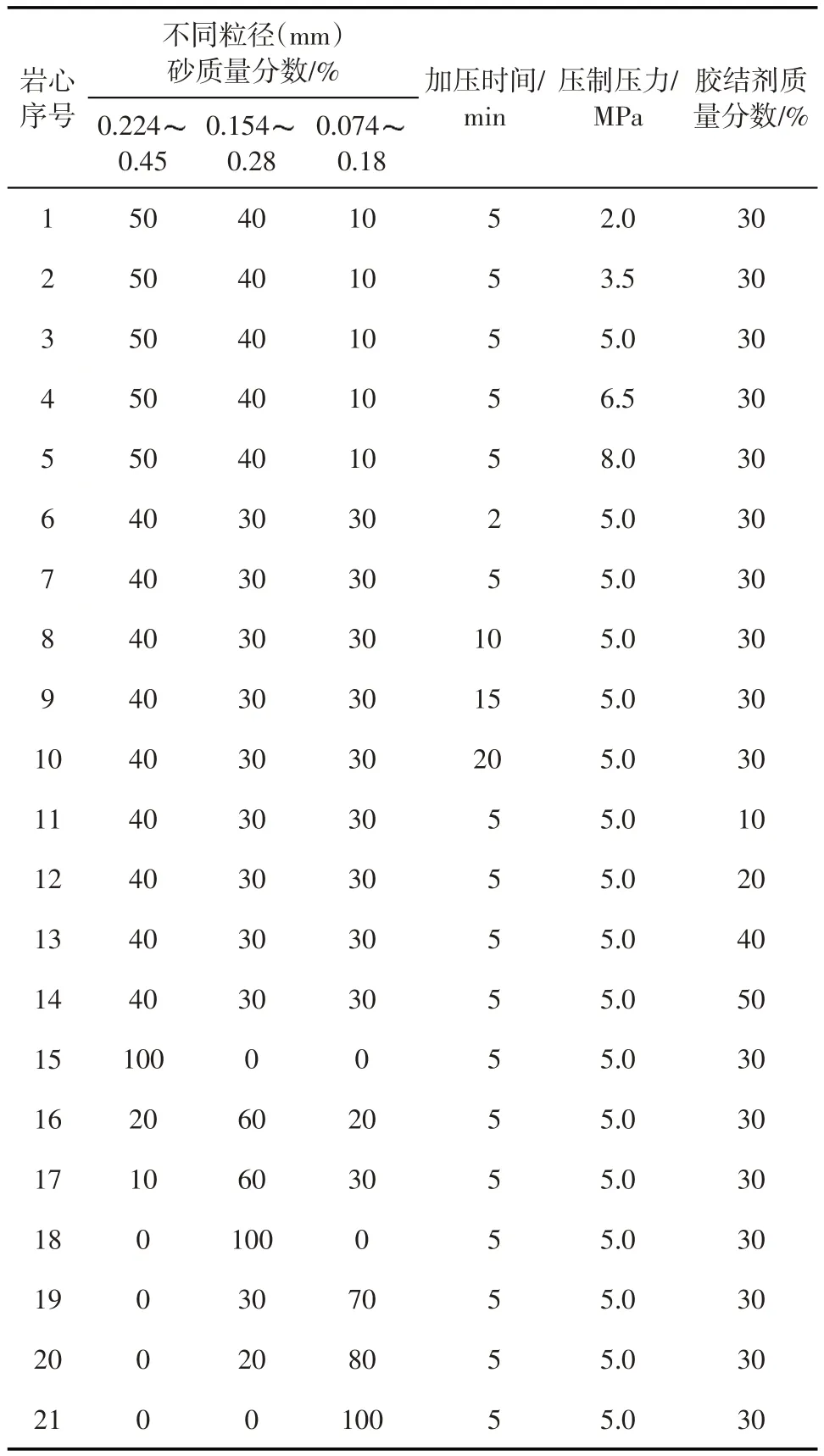
表1 岩心配比设计正交方案

2 结果与讨论

2.1 岩心物性参数影响因素

2.1.1 不同粒径石英砂加量

不同粒径石英砂加量对岩心孔隙度、渗透率和粒度中值的影响见图1。不同粒径石英砂加量是影响岩心物性参数的重要因素。岩心物性参数的测试值受到3种粒径砂粒用量的共同作用。由图1中的相关系数可知，0.224数0.45 mm、0.074数0.18 mm粒径石英砂加量对岩心孔隙度、渗透率和粒度中值的影响较大。

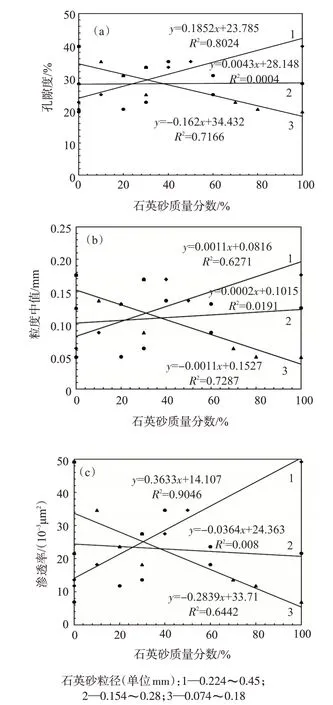
图1 岩心孔隙度（a）、粒度中值（b）、渗透率（c）与不同粒径砂加量的关系

2.1.2 压制压力与加压时间

压制压力与加压时间是人造岩心两个重要的制备参数。随着压制压力或加压时间的增大，岩心孔隙度、渗透率和粒度中值逐渐减小（图2）。随着压制压力持续增大，砂砾之间接触强度增大，部分砂砾压碎、破裂，孔喉结构改变较为明显；随着加压时间的增大，压实作用表现得更加充分，颗粒间距离随时间的增加而逐渐减小，颗粒表面的胶结剂移动也更加充分，从而使岩心渗透率、孔隙度和粒度中值不断减小。

图2 岩心孔隙度、渗透率和粒度中值与压制压力（a）、加压时间（b）的关系

2.1.3 胶结物加量

天然岩心中的碎屑颗粒主要是由胶结物胶结成坚硬的岩石，因此胶结物的加量和胶结类型对岩石的物性和储集性有重要影响［1］。人造岩心中碎屑颗粒的胶结强度及物性参数受到胶结剂用量的影响。由图3可知，在一定用量范围内，随着胶结剂加量的增大，岩心孔隙度、渗透率和粒度中值逐渐减小。

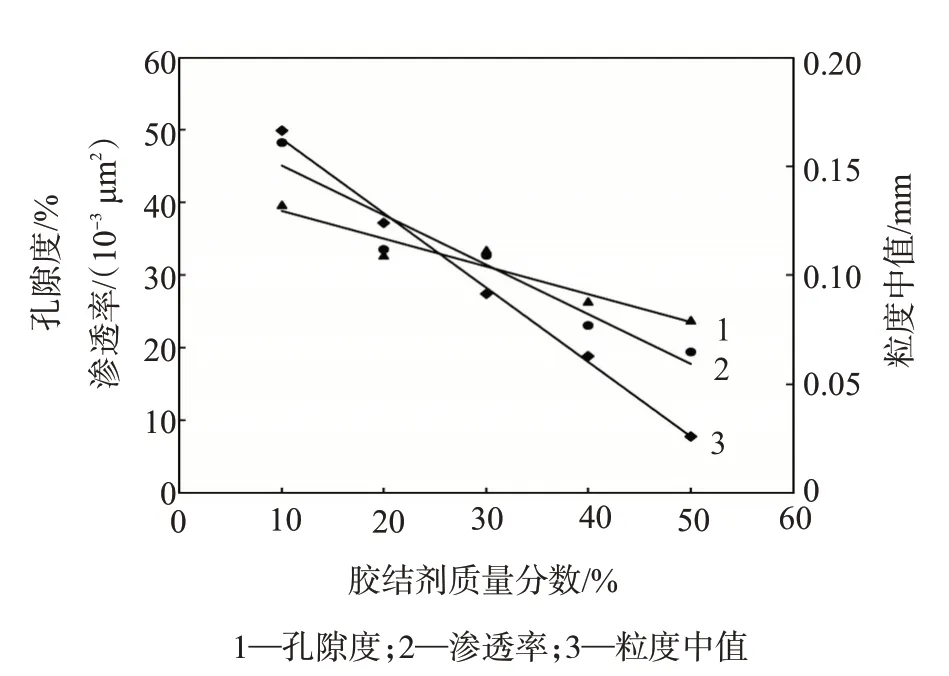
图3 岩心孔隙度、渗透率和粒度中值与胶结剂加量的关系

岩心各特性参数是各种因素综合作用的结果，且各因素影响程度不同，仅盲目调整某一单因素或几个因素来同时控制多目标参数是不可行的。

2.2 基于灰色关联法的人造岩心物性参数控制参数分析

考虑到影响人造岩心物性参数的影响因素主要有砂型配比、胶结物加量、压制压力、加压时间等，制作不同物性参数的人造岩心通常是由改变这些影响因素的种类或水平来实现。本次岩心制作未设具体岩心要求，仅作为通用方法的研究。若需要添加黏土、碎屑等其他矿物，或对润湿性有要求，则需要增加影响因素个数。灰色关联分析法［8］是一种多影响因素统计分析方法，以各种影响因素的样本数据为依据，用灰色关联度的大小来描述影响因素之间联系的强弱与顺序关系。

（1）预考虑的影响因素与孔隙度的关系。灰色关联法计算步骤参考文献［8］，用均值法作为去量纲方法，分辨系数ρ取0.1，计算得到不同粒径（0.224数 0.45 mm、0.154数 0.28 mm、0.074数 0.18 mm）砂加量、加压时间、压制压力和胶结剂加量与孔隙度的关联度分别为 0.4847、0.5626、0.4367、0.5325、0.5779、0.5783。预考虑影响因素按关联度从大到小依次为：胶结剂加量>压制压力>0.154数0.28 mm砂加量>加压时间>0.224数0.45 mm 砂加量>0.074数0.18 mm砂加量。

（2）预考虑的影响因素与渗透率的关系。不同粒径（0.224数 0.45 mm、0.154数 0.28 mm、0.074数0.18 mm）砂加量、加压时间、压制压力和胶结剂加量与渗透率的关联度分别为0.4809、0.4683、0.4124、0.4495、0.4698、0.4710。预考虑影响因素按关联度从大到小依次为：0.224数0.45 mm 砂加量>胶结剂加量>压制压力>0.154数0.28 mm砂加量>加压时间>0.074数0.18 mm砂加量。

（3）预考虑的影响因素与粒度中值的关系。不同粒径（0.224数 0.45 mm、0.154数 0.28 mm、0.074数0.18 mm）砂加量、加压时间、压制压力和胶结剂加量与粒度中值的关联度分别为0.4421、0.4657、0.3436、0.4546、0.4556、0.4455。预考虑影响因素按关联度从大到小依次为：0.154数0.28 mm 砂加量>压制压力>加压时间>胶结剂加量>0.224数0.45 mm砂加量>0.074数0.18 mm砂加量。

由灰色关联法计算结果可知，胶结剂加量和压制压力对孔隙度影响程度大；粒径为0.224数0.45 mm 砂加量对渗透率影响最大；0.154数0.28 mm 砂加量对粒度中值影响最大；0.074数0.18 mm砂加量对孔隙度、渗透率和粒度中值的影响最弱。应用最为广泛的石英砂环氧树脂胶结岩心是通过粒度调节控制渗透率、孔喉比，通过调节胶结物用量和压力控制孔隙度［3］，物性参数控制因素与灰色关联分析得到的主控影响因素相同。但仅改变单一因素来实现对多目标参数的定量控制，明显存在缺陷。

2.3 基于BP神经网络原理建立人造岩心配比设计模型

人造岩心物性参数受制于多种因素的影响，其中部分影响因素之间也存在某种函数关系，无法建立以目标参数为导向、精确的解析关系式。笔者采用基于人工智能原理的神经网络方法，建立人造岩心配比设计数学模型。部分BP算法［4］如下（网络误差与权值调整公式）。

输出层输出向量用O表示，其中列向量Ok为输出层第k个神经元对应的输出向量；期望输出向量用d表示，其中列向量dk为输出层第k个神经元对应的期望输出向量；输入层到隐含层之间的权值矩阵用ν表示，其中列向量νij为由输入层第i个神经元输入隐含层，在隐含层中第j个神经元对应的权向量；隐含到输出层之间的权值矩阵用w表示，其中列向量wjk为由隐含层第j个神经元输入输出层，在输出层中第k个神经元对应的权向量。i表示输入神经元个数；j表示隐含层神经元个数；k表示输出神经元个数。BP 算法中，各层权值调整公式相同，均由3个因素决定，即：学习率η、本层输出的误差信号δ以及本层输入信号y（或x）。三层感知器的BP算法权值调整计算公式为：

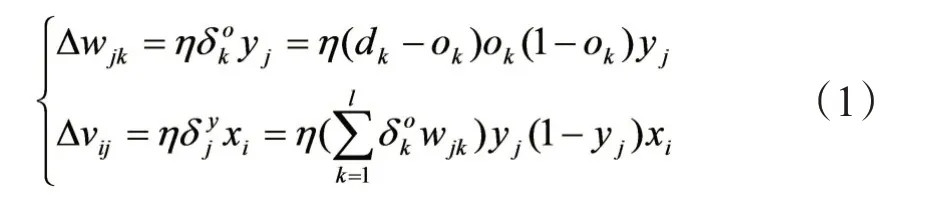
对于多层感知器，设共有h个隐层，按前向顺序各隐层节点数分别记为m1，m2，…，mh，各隐层的输出分别记为y1，y2，…，yh，各层权值矩阵分别记为w1，w2，…，wh，wh+1，则各层权值调整计算公式如下：

输出层：

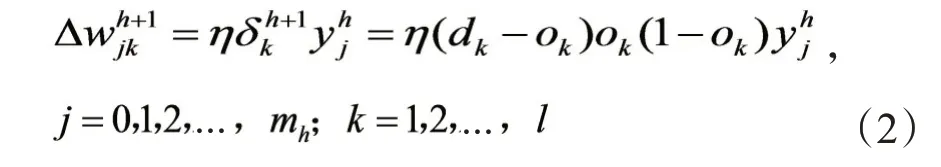
第h隐层：

按以上规律逐层类推，则第一隐层权值调整计算公式为：

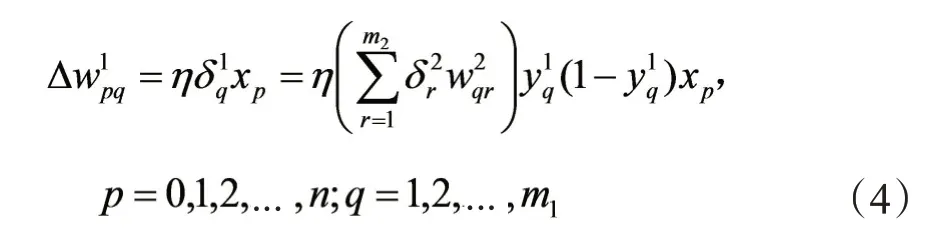
其中，Δ为网络权值的调整量。

使用最常用的输入层—隐含层—输出层三层BP 神经网络结构。输入参数有孔隙度、渗透率、粒度中值、压制压力和加压时间；输出参数有胶结剂加量和粒径为0.224数0.45 mm、0.154数0.28 mm、0.074数0.18 mm砂加量；隐层节点数根据删除法和扩张法确定［9］。设置BP 网络参数，包括目标精度、最大训练次数、网络训练效率值、网络动量因子值等。观察网络误差随训练次数变化图是否达到预设精度要求。如未达到预设精度，可通过调整训练函数、传递函数、训练效率值、目标精度等参数，直至达到目标精度且训练时间较短，利用模型计算胶结剂加量和3 种粒径砂加量，将其与实验加量值对比，检验模型的计算误差。

通过多次调试BP 模型网络参数，当隐层神经元个数为12、目标精度为0.0001、网络训练效率值为0.1，BP 网络最大训练次数为80000 次时，计算精度与训练时间较为理想。

由自编程序进行BP神经网络建模。BP神经网络结构见图4，岩心中不同粒径砂加量、胶结剂加量计算值与实验值的比较见图5，网络误差随训练次数变化见图6。通过比较21块岩心不同粒径砂在模型中计算得到的配比加量和前期制备岩心的实验加量（图5）可知，计算值和实验值重合度很高。观察图6，网络误差随训练次数的增加逐渐降低，达到目标精度，说明多次调试模型后，模型的稳定性和精度较为理想。

图4 BP神经网络结构

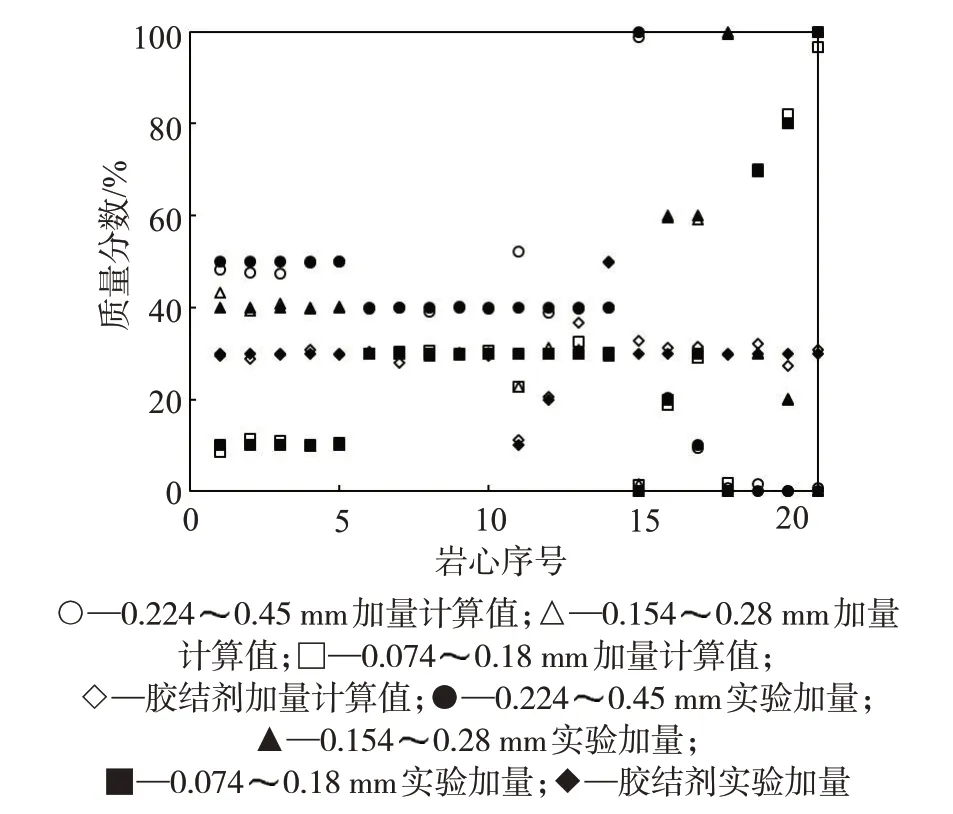
图5 岩心中不同粒径石英砂加量、胶结剂加量计算值与实验值的比较

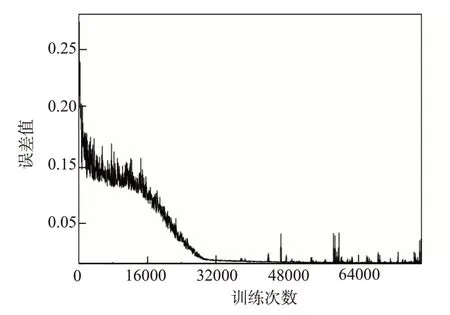
图6 网络误差随训练次数的变化

设定10块岩心物性参数期望值，由模型计算不同粒径砂加量和胶结剂加量（表2），并以此为据制备岩心。由制备岩心的物性参数测值（表2）可见，岩心期望物性参数值与实验测值的平均相对误差在10%以内。为提高精度，可增加岩心配比组数、岩心个数，继续充实数据库，完善模型。

需要指出的是，分析岩心设计的影响因素时需要注意两点：（1）全面性。即全面考虑所有影响目标参数的影响因素，定性分析预考虑参数是否符合现有的理论认识，判断预选影响因素的合理性。（2）数据化、定量化。数据是建立复杂函数关系的载体。用数据表征所有考虑到的影响因素，进行定量研究。

表2 10块岩心不同粒径砂配比计算结果与测试检验*

3 结论

预考虑影响因素的全面性和影响因素数据化、定量化是建立模型的基础。影响人造岩心物性参数的影响因素主要有砂型配比、胶结物加量、压制压力和加压时间等。胶结剂加量和压制压力对孔隙度影响程度大；粒径为0.224数0.45 mm石英砂加量对渗透率影响最大；0.154数0.28 mm石英砂加量对粒度中值影响最大；0.074数0.18 mm石英砂加量对孔隙度、渗透率和粒度中值的影响最弱。基于实验数据与BP 神经网络原理，建立了人造岩心配比设计数学模型。根据模型计算结果制备人造岩心的物性参数与计算值的误差较小。为提高模型计算的稳定性，减小制备误差，可增加岩心配比组数和岩心个数，充实数据库，完善数学模型。