带有扰动的一维波动方程的镇定

邢永峰，武晓辉

(山西大学 数学科学学院， 太原 030006)

近几十年来，分布参数系统已被广泛研究。例如,文献[1-2]考虑了含源项和阻尼项的非线性波动方程的解在有限时间内爆破。文献[3]通过边界控制可以使得波方程系统稳定。对于带有内部和外部干扰的波方程的控制问题也得到广泛研究[4-5]。在控制理论中,处理扰动的技术方法有许多，例如鲁棒控制[6]、自适应控制[7]、滑模控制[8]、李雅普诺夫方法[9]等，然而它们多数基于一个精确的模型，通常针对最坏的情形，这样使得控制器的设计相当保守且不能合理地利用资源。

为了解决这一问题，自抗扰控制器首次被韩京清提出[10]。自抗扰控制技术设计理念明显不同于前者，它主要是通过输出把干扰估计出来，之后在反馈环节消除。它解决了响应速度与超调性之间的矛盾，通过补偿消除了模型未知部分和外部未知扰动综合对控制对象的影响，实现了动态系统的反馈线性化。在波系统的控制器设计中，自抗扰控制技术已经被广泛应用于处理系统未知的内部和外部扰动[11-12]。特别地,文献[13]利用自抗扰控制技术考虑了边界含有未知扰动的波方程的镇定。本文在此基础上，进一步考虑了含有内部和未知边界扰动的波动方程的镇定。首先，通过量测位移的加权平均来设计扩张状态观测器对扰动进行估计；其次，设计相应的反馈控制器来使系统镇定；最后，证明闭环系统解是渐近稳定的并且通过数值仿真进一步验证本文的结论。

系统由下面方程给出：

(1)

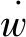
1 控制器的设计及主要结论

首先估计扰动d(t)。对Y(t)关于t求两阶导，并结合式(1)：有：

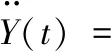
(2)

令Y1(t)=Y(t),则式(2)可以写成如下微分器形式：

(3)

设计如下状态观测器来估计干扰：

(4)

其中，g∈C1[0,∞)是时变的增益函数，并且满足：

(5)

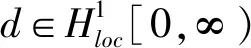
(6)

令

(7)

则由式(3)和(4)可知，误差系统(7)满足：

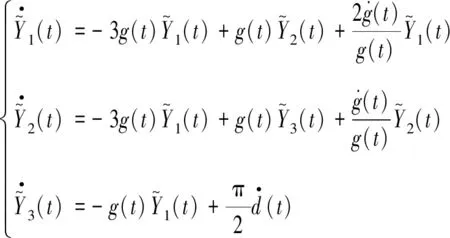
(8)

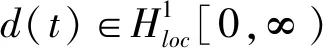
当t→∞时，

(9)

证明根据存在唯一性定理[14]可知系统(8)的解存在且唯一。下面证明系统(8)解的稳定性。

容易验证，如下矩阵G是Hurwitz矩阵：

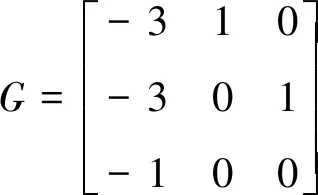
(10)

因此，存在正定矩阵V，使得GΤV+VG=-I3成立，其中I3为3阶单位矩阵。

构造 Lyapunov 泛函如下：

(11)

则有，

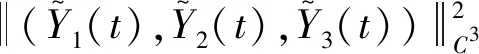
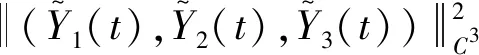
(12)

其中λmin与λmax分别为矩阵V的最小与最大特征值。L(t)关于t求导，并结合式(8)，有：

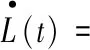
(13)

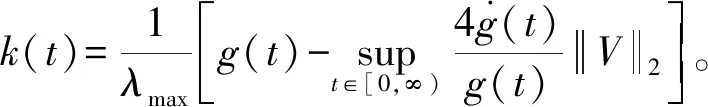
当t→∞时,k(t)→∞

(14)

因此，存在t0>0使得

k(t)>0， ∀t≥t0

(15)

结合式(13)，有：

∀t≥t0

(16)

直接计算可得：

(17)

由于式(14)，当t→∞时，式(17)右边第一项收敛到0，对式(17)右边第二项运用 L’Hospital法则，得到：

(18)

从而，当t→∞时，

(19)

(20)

其中k>0是一个设计常数。由式(1)、(4)以及(20)可以得到如下闭环系统：

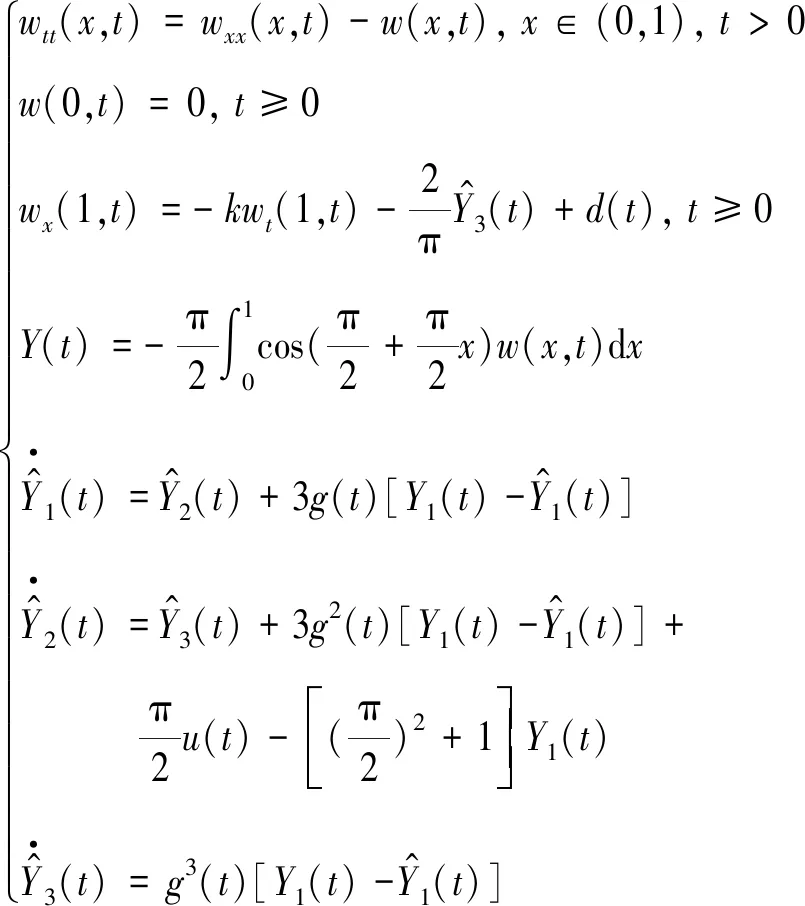
(21)

2 闭环系统的适定性与稳定性

注意到系统(8)，直接计算可得式(21)等价于

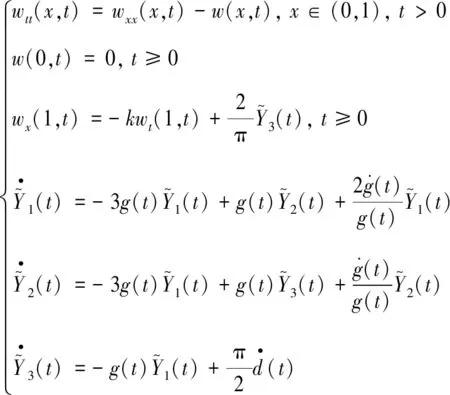
(22)

(23)

〈(f1,g1),(f2,g2)〉X=

∀(fi,gi)∈X,i=1,2

(24)

将系统(23)写成如下抽象形式：

(25)

其中：B=(0,δ(x-1))，δ(·)是Dirac分布，算子A定义如下：

f(0)=g(0)=0,f′(1)=-kg(1)}

(26)

定理1算子A由式(26)定义，g(t)满足式(5)，d(t)满足式(6)，则对任意的初值(w0,w1)∈C([0,∞);X)，系统(23)存在唯一的解(w,wt)∈C([0,∞);X)。此外，

(27)

证明1) 对任意的(f,g)∈D(A)，有：

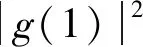
(28)

所以，A在X中耗散。

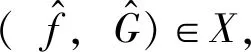
(29)

其中，

(30)

根据Sobolev嵌入定理[15]可知：A-1存在且在X中是紧的。由Lumer-Phillips定理[16]得：A在X中生成压缩C0-半群。

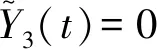
(31)

此时，为系统(23)构造如下Lyapunov泛函为：

F(t)=NE(t)+φ(t)+αψ(t)

(32)

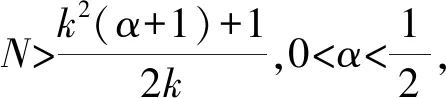
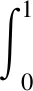
(33)

以及

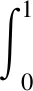
(34)

直接计算可得：

(35)

F(t)关于t求导,应用Young不等式，我们有

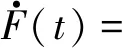
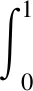
αw(1,t)wx(1,t)≤

(36)

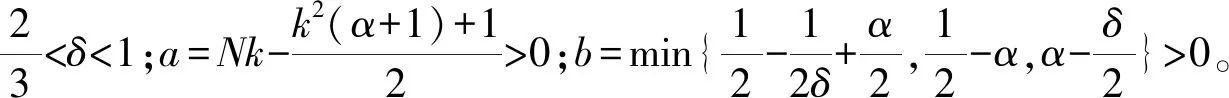
∀t≥0

(37)

因此，

∀t≥0

(38)

所以A在X上生成指数稳定的C0-半群eAt。

3 数值仿真

进行数值模拟来说明理论结果。在仿真中，采用中心差分的方法对空间和时间进行离散。设计常数k=1,空间步长dx=0.005，时间步长dt=0.005。时变增益为:

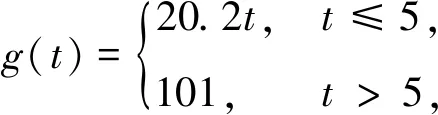
(39)

扰动

d(t)=cost+0.1sin5t

(40)

初始条件如下：

w0(x)=sinπx

w1(x)=cosπx

(41)

图1表示系统的位移，系统(21)的状态收敛到0。图2中，绿色线代表干扰，红色线代表它的估计值。从图中可以看出：一定时间后，干扰可由扩张状态观测器很好地估计出来。与文献[11]和文献[13]中的常增益扩张状态观测器相比，采用变增益扩张状态观测器可以有效抑制超调的产生。由图2可以看出：干扰和干扰的估计始终在同一数量级。

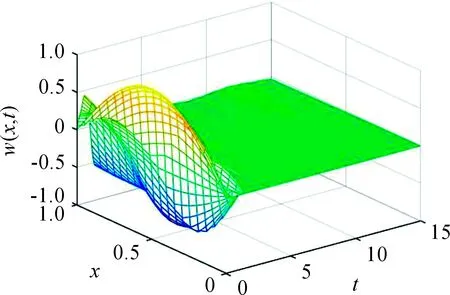
图1 带有扰动的一维波动方程的镇定

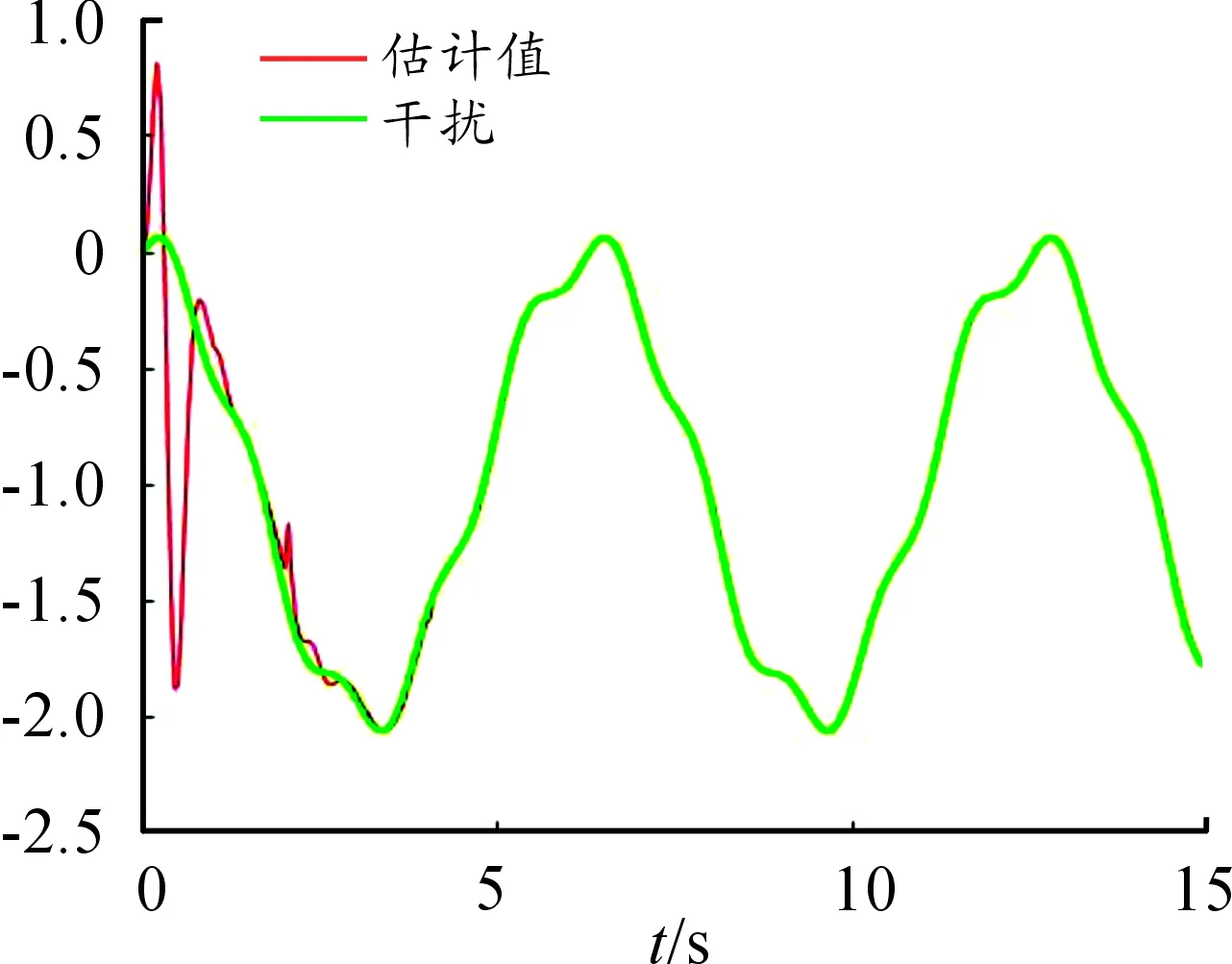
图2 干扰和它的估计值

4 结束语

本文基于量测位移的加权平均设计了时变的扩张状态观测器对系统的干扰进行估计，从而设计了一个控制器来稳定带有干扰的一维波动方程。设计的扩张状态观测器对扰动具有较为准确的估计，相应的反馈控制器的设计使得系统稳定。通过算子半群理论和李雅普诺夫方法证明了系统解的适定性和渐近稳定性。从理论和实践两方面验证了此方法的有效性。我们的方法可以延伸到只通过量测系统状态的加权平均来对系统做输出反馈控制，这也是今后研究和努力的方向。