农机作业履带式行走张紧系统的自适应控制策略
杨张利
(重庆电子工程职业学院, 重庆 401331)
随着我国经济的快速发展,农机作业自动化程度已取得了明显的进步,履带行走装置因其接地比压低、转弯半径小、牵引力大与爬坡能力强等优势在农业机械作业中得到广泛的应用,特别是在大中型自行式机械中应用比较普遍。履带行走性能对农机作业效率有举足轻重的影响。如履带张紧装置的预张紧力偏低或者太小,必然导致履带松驰,履带失去张紧作用,从而引起履带上方的跳动与振动,使摩擦力增加,致使机件的磨损增大;如履带张紧装置的预张紧力过大,必然导致履带刚性增加,过大的刚性使张紧装置失去缓冲功能,增加履带行走机械的内摩擦力,因为丧失缓冲功能,轻则使履带行走能耗增大并加速履带磨损,重则会在行走过程中因受到外界冲击而导致履带断裂,甚至在行走过程中产生履带脱轨等重大事故。因此,合理的张紧力控制对农机作业有重大作用,被公认为是履带行走装置的核心技术[1-4]。以履带弹簧张紧为例,借助油压机使弹簧获得一定的预张紧力,如果履带在行进中遇到冲击时,那么弹簧就可以起到缓冲作用,将外界冲击力的变化直接转换为弹簧的伸缩运动,从而避免履带行走机构受到外界冲击力影响。针对上述存在的问题,以下对履带式农机作业行走过程中如何保持最佳张紧状态从控制论角度针对控制策略进行探讨。
1 张紧过程的控制论特性
农机作业的工作环境是非常复杂的,野外作业有很多因素是不可控的,在不同行驶状态和路况下行走具有很大的不确定性,而行走机构的设计是在参数确定的情况下完成的,因此张紧装置中的控制系统显得特别重要。只有张紧系统的控制策略与张紧过程的控制论特性匹配才能确保高效率的农机作业,保证行走机构一直保持在最佳张紧力状态下运行。张紧过程表现出如下控制论特性:农机作业中履带张紧过程受众多不确定与难以预测因素的影响,过程参数具有时变性、随机性和未知性;履带张紧过程具有时滞与高度非线性特性,其时滞特性因受到不确定性因素影响,且时滞特性本身同样具有时变性和未知性;履带张紧过程具有惯性特性,过程复杂,变量众多,并且变量之间存在着复杂的关联性;农机野外作业环境存在各种干扰的不确定性、随机性、多样性和未知性。野外地质情况相对变化较大,导致履带张紧力难以达到均匀和稳定,经常引起张紧力波动。上述特性表明,履带张紧过程中充满了不确定性和复杂性,因此对张紧过程采用数学方法实施建模控制是难以取得期望控制效果的,有必要探讨与其过程控制论特性相匹配的控制策略与控制算法[5-9]。
2 控制策略与控制算法
2.1 控制策略选取
面对张紧过程的不确定性、参数时变性、高度非线性和时滞特性等控制论特性,从自动控制理论角度考虑,可供选择直接用于控制的策略并不多。如采用传统与近代控制理论的控制策略,其控制器的分析与设计都是基于精确的数学模型,而张紧过程是难以数学建模的,因此对张紧过程采用数学手段描述的定量范式控制策略几乎是不可能的,即使忽略一些难于处理的因素,勉强地建立了数学模型,其实施的控制效果也不可能令人满意。随着自动控制理论和人工智能的发展,给控制策略选择提供了全新的控制思路。如神经网络控制,但因受张紧过程不确定性因素影响,很难从事先试验中获得学习试验样本。对张紧过程而言,因方法的局限性,该控制策略并非是有效的控制策略。专家控制系统可处理各种精确、定量、模糊与定性的信息,但很难建立完备的知识库,此外,因张紧过程存在不确定性,在特征信息采集与表达等方面显得更加难以实现,所以专家系统用于张紧过程控制并不现实。模糊控制基于模糊集合理论可以对张紧过程进行描述并归纳出控制规则,但张紧过程的复杂不确定性特性可能导致其隶属函数难于确定,可能导致难于归纳出适合于张紧过程控制的控制规则,从而难以实施优化控制。值得关注的是智能控制策略,该策略无须人工干预,在过程动态特性变化范围内,智能控制器可自主地驱动被控制过程,使其自动地达到期望的控制目标。仿人智能控制HSIC ( human simulated intelligent controller)[10]就是模拟人类控制行为的控制器,误差及误差变化率是可借助物理手段检测的,并且可采用产生式规则描述其控制行为与推理过程,能方便地基于广义控制模型设计控制器,将控制专家的知识和过程操作者的控制经验、智慧与技巧融入控制算法以改善控制品质,从而增强控制器的鲁棒性能,完美地协调张紧过程中相互矛盾的控制品质要求,因此HSIC控制策略应当是一种较理智的选择。
2.2 控制模型与控制模式
图1为基于知识的负反馈广义控制模型。

图1 基于知识的广义控制模型


图2 张紧控制过程的系统误差相平面
2.3 控制算法
由上述两种基本控制模式,基于图1所示的负反馈广义控制模型[11-14],可以构造出基于仿人智能的HSIC基本控制算法:
各符号的物理意义如图1所示:U为HSIC控制器的输出;e为过程系统误差。在基本算法中,em, j表示系统误差最大值的第j次峰值,Kp为比例系数,k为抑制系数。
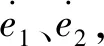
3 实验仿真及其结果分析
3.1 实验仿真
考察控制策略的自适应性,实质上就是考察该控制策略的鲁棒性能。对过程跟踪控制而言,鲁棒性强的控制器有很强的自适应性,其跟踪性能很少受外部干扰和内部控制参数变化的影响。对张紧过程恒值控制系统而言,外部干扰和内部控制参数变化也同样几乎不影响其控制品质。以下借助实验仿真验证基于仿人智能控制策略的强鲁棒性能。鉴于张紧过程是一个具有惯性的时滞过程,因此可以用1阶惯性加时滞环节对其过程动态特性进行描述。考察张紧过程对不同控制策略的过程响应,就可比较不同控制策略的强鲁棒性能,为了方便,选择以PID控制策略(控制算法1)为参照与仿人智能控制策略HSIC(控制算法2)相比较,通过改变过程的结构阶次以及施加外部干扰模拟作业现场工况的变化,如果其调节时间短、响应时间快、运行平稳、不存在超调或者超调小和稳态控制精确度高,那么该控制策略因其强鲁棒性一定是可取的。
设1阶惯性时滞过程模型为W(S)=Ke-τs/(Ts+1),基于 Matlab环境,借助Simulink搭建仿真模型,在阶跃输入为2的信号作用下,取K=7.8,T=74,τ=20,分别采用PID和HSIC控制同一过程,其过程响应如图3所示。
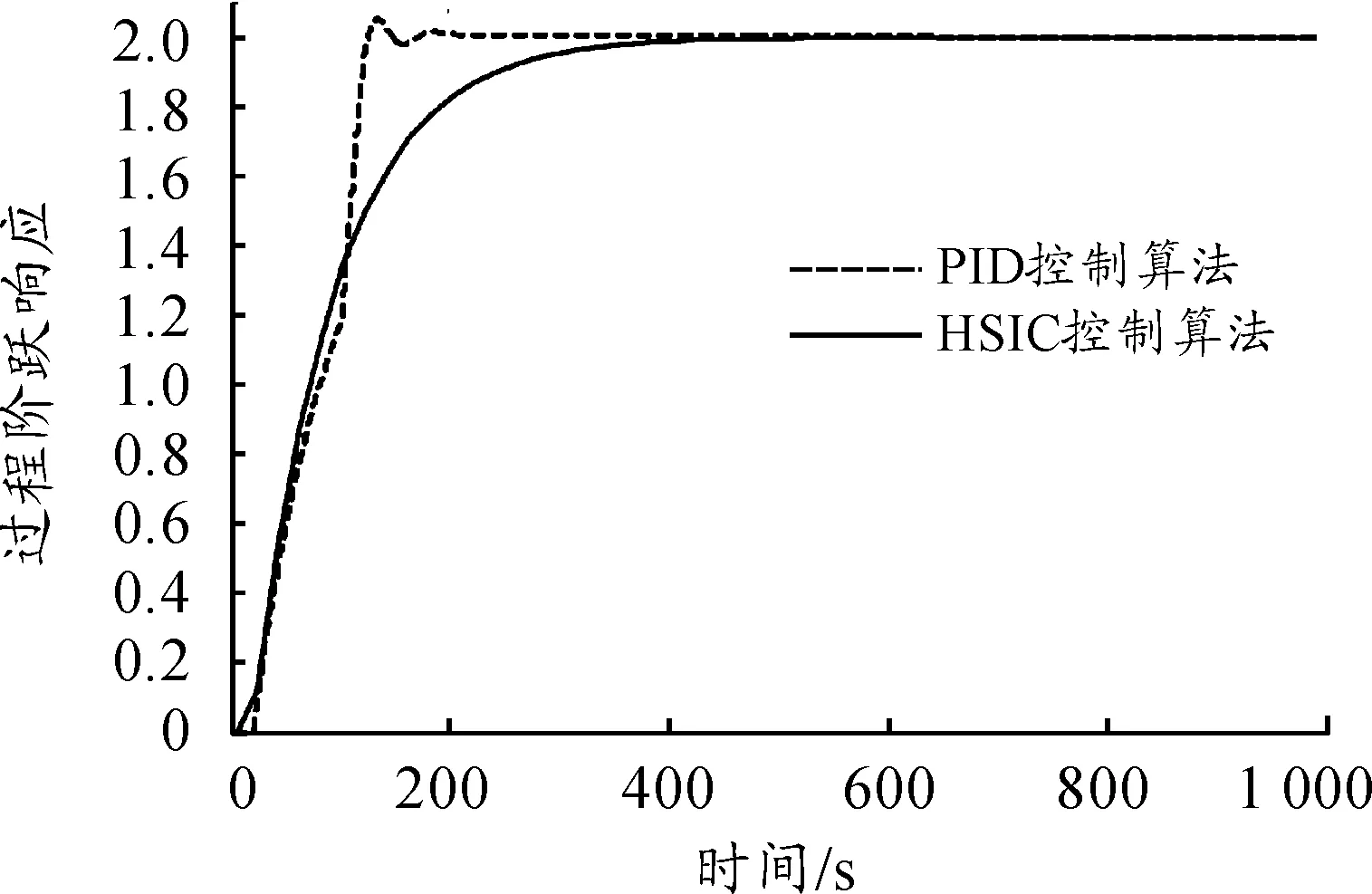
图3 PID和HSIC控制下的过程响应
从过程控制参数变化角度考察控制算法的鲁棒性能。如果在原一阶惯性时滞过程模型中增加一个惯性环节,即过程模型变为W1(S)=Ke-τs/(Ts+1)(5s+1)时,当原模型参数仍然保持不变,即K=7.8,T=74,τ= 20,显然其过程模型已经由1阶惯性时滞过程变为2阶惯性时滞过程,过程阶次也已经由原来的1阶变为现在的2阶过程,当然,过程参数也相应地产生了变化,在保持上述实验仿真条件不变的情况下,两种控制算法的过程响应曲线如图4所示。

图4 增加惯性环节后的过程响应
从抗外部干扰性能角度考察控制算法的鲁棒性能。在保持上述实验仿真条件不变的情况下,在t=100 s施加一个宽度为10 s、幅度为0.5的定值扰动信号,两种控制算法在外部干扰下的过程响应如图5所示。
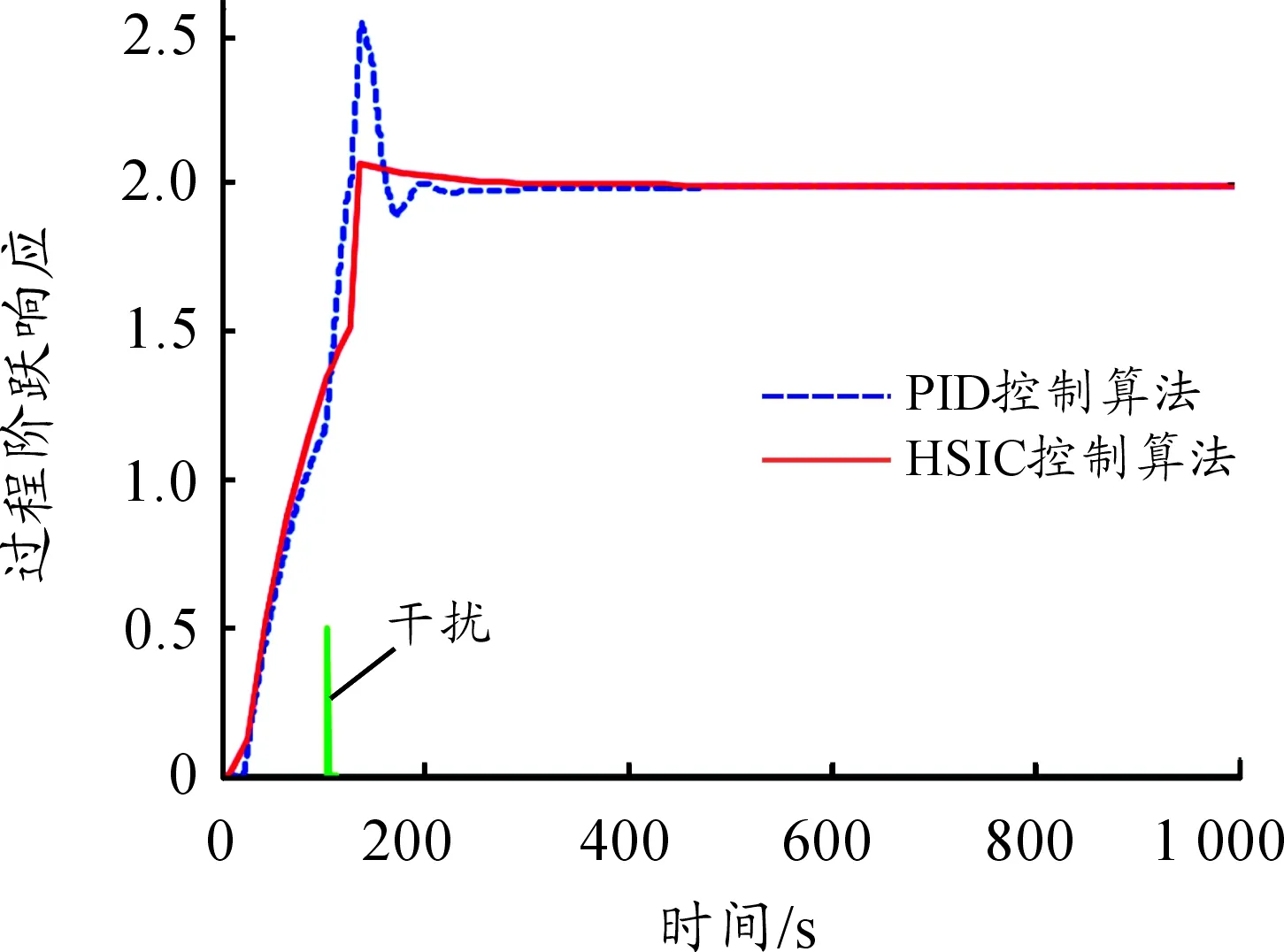
图5 外部干扰下的过程响应
3.2 实验结果分析
从图3的过程阶跃响应曲线可知,PID控制算法1出现振荡与超调量,HSIC控制算法2的过程平稳,不存在振荡与超调量,显然HSIC 控制更适应于张紧过程的控制。对比分析图4可知,即使原1阶惯性时滞过程增加一个惯性环节后,HSIC控制算法仍能对过程实现平稳的控制,既不产生振荡也不产生超调,其控制过程的响应速度与调节时间也是令人满意的。对比分析图5可知:HSIC控制产生的超调量是非常小的,而且没有产生任何荡频;对PID控制而言,不仅仅产生大幅度的超调,而且还产生振荡,并且其产生的振荡频率和幅度均比较大。由上述实验结果分析可见,与PID控制相比,基于仿人智能的HSIC控制策略鲁棒性能强,具有很好的适应过程参数变化与抗外部干扰的性能。
4 结束语
农机作业履带式行走张紧控制系统因其张紧过程具有不确定性、参数时变性、高度非线性和时滞特性等过程控制论特性,从自动控制理论角度考虑,可供直接选择应用的张紧控制策略并不多。本文探讨的张紧过程自适应控制策略的强鲁棒性能表明:基于仿人智能的HSIC控制策略对农机作业履带式行走张紧控制跟踪具有自适应性,是一种比较好的可供张紧控制系统设计参考的控制策略。

