水流作用下的渔网水动力数值方法研究
胡 克,耿宝磊,赵 旭,沈文君
(交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 工程泥沙交通行业重点实验室, 天津 300456)
*通讯作者:耿宝磊(1980-), 男,副研究员,主要从事港口及海洋工程水动力研究。E-mail:tksgengbaolei@163.com
随着人口的急剧增长,对于食品的需求也在不断增加。海洋面积约占地球面积的70%,目前,人类食品的主要来源仍来自陆地,海洋所提供的食品来源比重很小,未来海洋养殖业将会成为人类食品的主要来源之一。因此,网箱在波流载荷下的水动力问题将会成为未来研究的重点。
网箱通常放置在有水流的地方,以便改善网箱内的水质,同时进行网箱内氧气的更新,所以流速对于网衣的水动力和容积影响是研究人员关注的重点。Aarnses[1]通过对重力式网箱进行的拖曳试验研究了作用于网箱上的阻力以及网衣的变形和箱体内的流速衰减规律。目前,网衣数值结果比较多的试验是Lader[2]进行的三维网衣在不同流速和不同配重下的水动力试验,通过研究发现,网衣的受力与网衣的变形相互影响;网衣的受力受到雷诺数的影响很大;在计算柔性网衣的受力时,如果使用基于弹性很小的单片网衣得到的阻力公式计算,将会产生很大的误差。此外,还通过试验测量了不同流速和配重下的网衣升力和阻力,并拟合出升力和阻力相对雷诺数的经验公式。除了试验研究外,Schlichting[3]最早将尾流场的概念描述成“尾流远场的平均速度损失”。 Løland[4]通过研究发现,水流经过网平面后,在网衣的宽度范围内是呈均匀分布的,而且衰减后的流速并不随着远离网衣的距离增大而明显减小。此外,他还根据研究成果推导出了速度衰减的经验公式[5]。
与大尺度结构波浪力计算方法不同[6],网箱与牧场周围围栏设施[7]等属于小尺度结构物。计算网衣水动力的模型主要有两种:Morison方程模型和网平面模型。对于Morison方程模型来说,是将每根网线看作圆柱体,根据圆柱的雷诺数和KC数来计算网衣的水动力系数,进而根据Morison方程求解水动力。对于网平面模型,是先将网衣按照不同密实度(Solidity Ratio)和与来流攻角测量出网衣的法向和切向力系数,再将网箱上每个网目按照响应的法向和切向力系数计算出来。
目前,使用Morison方程计算网衣的方法较多,例如Huang[8]、赵云鹏[9-10]和许条建[11]等都使用了这一方法计算波流作用下的重力式网箱。在他们的水动力计算模型中都是在每个迭代步后根据雷诺数更新水动力系数的,在对网衣结构的模拟是基于集中质量点法的,这种方法假定网衣的质量集中在节点处,相邻节点之间使用弹簧连接并模拟刚度。另一方面,Moe[12]和Li[13]则使用有限元方法来模拟网衣合股线结构,但是水动力模型进行了简化,即根据流速和网衣合股线直径计算出雷诺数再选取固定的阻力系数计算网衣的水动力。除了Morison方程以外, Kristiansen[14]则基于网平面模型用于计算网衣的水动力。在他对网衣研究成果中,首先根据Rudi[15]进行的单片网衣试验结果,使用傅里叶级数的方式拟合出升力系数和阻力系数关于网衣密实度和攻角的经验公式,再计算出网衣的水动力。在他的网衣模型中也是集中质量点法来模拟网衣的结构。本文尝试使用一种新的方法:根据网衣的物理特性,基于有限元方法对网衣结构进行离散,建立相应的系统控制方程,计算求解网衣的动力响应,并基于文献[14]中的水动力模型,准确求解出网衣的水动力。
为了实现这一方法,本文基于ABAQUS用户子程序的二次开发技术,采用FORTRAN语言,编写了适合于网衣的水动力计算子程序。根据这一方法,先通过每个迭代步输出的节点信息(包含速度和加速度)计算出网目雷诺数以及与来流的夹角,然后根据试验所得的单片网衣阻力和升力系数,计算出每个网目的阻力和升力,进而得到各个时刻下的整个渔网的水动力。
1 基本理论介绍
1.1 运动方程
当网箱处于波流作用下,其结构的动力平衡方程可以表示成为

(1)
Fext=G+fb+fw+fc
(2)
式中:[m]为质量矩阵,[c]为阻尼矩阵,[k]为刚度矩阵。结构的外载荷用Fext表示,如式(2)所示,共包含四个部分:重力G,浮力为fb,波浪力为fw,水流阻力为fc。
式(1)和式(2)中,重力可以由静态浮力计算得到,浮力fb由结构的瞬时浸没的浮圈结构计算得出。
1.2 水动力模型
对于网衣结构,本文使用的是网平面模型计算。每个网目上的升力和阻力都是按照如下公式进行计算的
(3)
(4)
Rudi等人[15]首先通过试验方法对平面网衣平面下不同来流攻角下,不同密实度的网衣进行阻力系数和升力系数测量,在试验中的网衣密实度Sn包括0.130,0.144,0.184,0.243和0.317,试验流速包括0.159,0.316和0.966 m/s。Kristiansen[14]对这次试验中的阻力和升力系数使用正弦行数曲线在不同攻角(θ)和网衣密实度(Sn)的网衣平面的阻力系数和升力系数进行拟合。得到的结果如下
CD=cd(α1cosθ+α3cos3θ)
(5)
CL=cL(b2sinθ+b4sin3θ)
(6)
在式(5)和式(6)中,α1和α3分别等于0.9和0.1,b2和b4分别等于1和0.1。cd、cL则参照文献[14]中的计算方法进行计算。
1.3 几何非线性理论
基于小变形假设,建立平衡条件时不必考虑物体位形的变化,因而应变可以采用位移的一阶偏导进行度量。在本文所处理的网箱变形中由于大挠度和大转动的存在,使其不满足小变形假设,在有限元求解中必须考虑几何非线性的影响。
1.3.1 应变-位移之间的关系
当结构需要考虑几何非线性时,应力与应变的关系可以写成
(7)

(8)
式中:[B0]是线性应变项,与位移{δ}e呈线性关系;[BL]是大位移应变项,是位移{δ}e的函数。
1.3.2 应力-位移之间的关系
单元内部应力增量和应变增量关系可以表示成为:
d{σ}e=[D]d{ε}e
(9)
式中:[D]为材料的本构关系矩阵。联合式(4)、(5)和(6)可以得到如下形式
(10)
式中:{ε*}e和{σ}e分别代表单元的虚应变和虚应力,{δ*}e为单元节点虚位移,{F}e为单元节点力。
联合式(7)和(10)可以得到
(11)
再对式(11)进行微分后可得
(12)
式(12)又可以写成
([k0]+[kσ]+[kL])d{δ}e=d{F}e
(13)
式(13)为几何非线性问题的求解方程。其中,[k0]是小位移线性刚度阵;[kL]为大位移非线性刚度阵;[kσ]是初始应力非线性刚度阵;以上三个刚度阵分别表示为
(14)
(15)
(16)
1.4 等效网目计算方法介绍
网箱的网衣在计算水动力时,由于实尺度网衣上的单元较多,因此很难将计算模型的单元数与实尺度的网衣单元保持一致,事实上,网衣计算模型需要简化。对于简化后的模型,应该保持质量和刚度与简化前一致,如式(17)~(18)所示
Mtruss=M
(17)
(EAsection)truss=ΣEkAsection_k
(18)
式中:A和Asection代表网衣合股线的投影面积和横截面积,M代表网衣的质量,E代表网衣的弹性模量。苏炜[16]和Moe[12]曾验证过使用等效网格将网目合并后计算网衣模型与试验模型中网衣的变形,并得到很好的计算结果,本文将基于这一方法简化网衣模型。

图1 浮筒分段浮力计算示意图Fig.1 Buoyancy calculation of floating collar′s segment
1.5 网箱体积计算方法介绍
网箱的体积变化直接影响到养殖物的生存空间,因此,对于网箱容积的变化是网箱水动力研究的主要部分,为了对网箱容积变化进行研究,首先将网箱在波流作用后的容积与静止时的网箱比值定义为网箱的容积变化率,如式(19)所示
(19)
式中:Cv为水流条件下网箱的容积变化率,Vc为波流作用下的网箱容积,V0为网箱在静止状态下的体积。
对于网箱的容积计算,本文使用的是如下计算方法:首先,将网箱沿中轴线等分为若干楔形体,而每个楔形体又近似看做为棱柱结构,将每个棱柱结构可以分为3个四面体结构,如图1所示。

图2 四面体示意图Fig.2 Sketch of tetrahedron
对于任意四面体OABC的体积计算方法(如图2所示),其计算公式可以写为
(20)
按照式(20)将图1中的三个四面体的体积计算出来以后再相加,就得到了一个棱柱的体积,最后再将网箱上每个棱柱的体积相加,就得到了此时网箱的容积。
1.6 流速衰减计算方法介绍
水流经过网衣平面后会出现流速减小的情况。Løland[5]曾经对流速衰减进行了研究,他将网箱分解成若干网片,并对流速通过网衣后的阻力进行了总结,得到了不同网衣密实度Sn下的网衣的流速衰减系数r和阻力系数之间的关系式,得出公式(21)的表达式
r=1.0-0.46Cd
(21)

图3 网衣水动力施加方法示意图Fig.3 Sketch of the method of hydrodynamic force acting on the twine
2 水动力施加方法介绍
本文使用的方法水动力模型是基于试验结果得到的,其水动力系数计算方法已经在1.2节中进行了阐述,在这里只介绍在ABAQUS中的网衣水动力施加方法。

3 计算结果分析与讨论
3.1 网衣疏密变化的比较
根据Moe[12]的介绍,计算的网衣模型的整体直径为1.435 m,深度为1.44 m,网目的边长为1.76 cm,合股线直径为2 mm,网衣的密实度是按照如下公式进行计算的
(22)
在式(22)中,d代表网衣合股线直径,λ表示网目边长。计算得出Sn=0.214,此外,根据Moe[12]提供的参数,网衣的刚度EI=8.2×107Pa。在网衣的最上端为刚性圆圈,且由均匀分布四个简支的支点固定。沉子为16个800 g、600 g和400 g的重块,根据Moe[12]的介绍,重块在水中的重量分别为6 N、4.5 N和3 N,在本文的计算模型中将以集中力的方式施加到网衣底部。为了研究不同网格数对于网箱水动力计算结果的影响,在本文中使用了两种网格数的网衣,分别为64×21和32×12。与Lader的试验模型相同,本文建立的网衣模型也是没有底部网衣的,两种网格的网衣模型如图4所示。
图5给出了两种数量的网格模型计算结果。在本文计算的流速中,共进行了三个流速:0.2 m/s,0.34 m/s和0.5 m/s。从总体上看,两种网格的计算结果在不同流速下较为相近,在流速为0.5 m/s时,计算值小于试验值,此时的相对误差为9.5%,这可能是由于此时的网衣变形最大,所以相对误差要大于流速较小的情况。对于升力,网箱的升力是通过网箱顶部固定的四个节点在垂直方向的合力减去沉子的重力后得出的。从趋势来看,数值模拟的结果与网箱的实验结果都是随着流速的增大而增大的。在流速为0.5 m/s时计算值与实验结果的相对误差较大,为10.8%。


4-a 64×214-b 32×12图4 网格对比Fig.4 Comparison of different grids of the net cage图5 网箱试验和计算的阻力和升力结果对比图(16×800 g)Fig.5 Comparisons of drag force and lift force between model tests and calculated result in numerical analysis(16×800 g)
图6中显示的是在流速为0.34 m/s情况下,通过不同网格数下网箱的变形情况与试验结果的比较可知,疏网格(32×12)与密网格(62×21)的变形大体上是一致的,同时结合阻力与升力的计算结果,可以使用疏网格计算网衣的阻力和变形情况。此外,为了节省计算时间,下面将使用疏网格(32×12)对网箱的水动力进行计算。
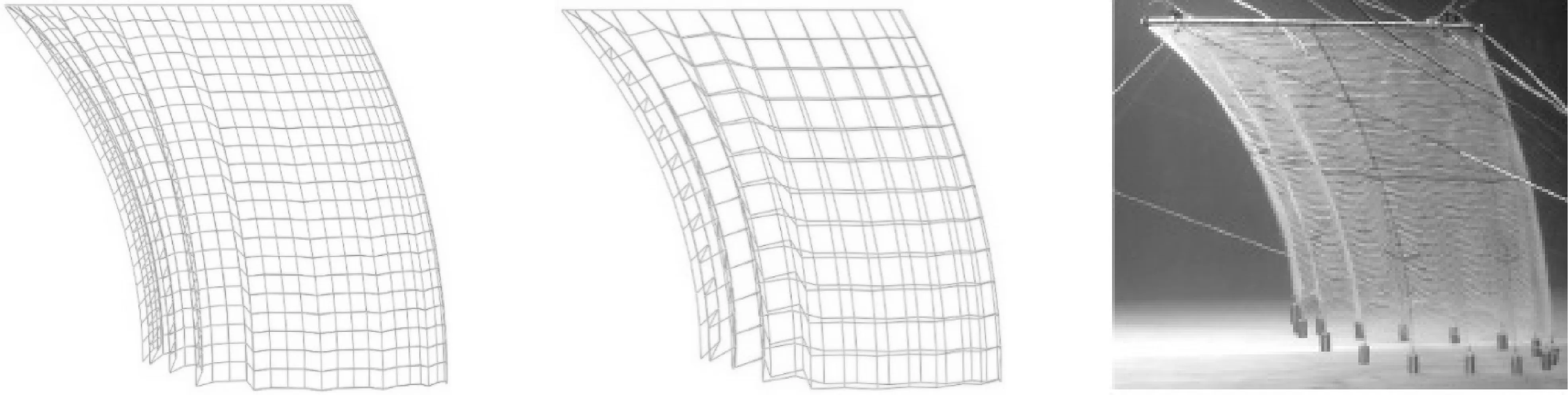

6-a 64×216-b 32×126-c 模型试验[5]图6 在流速为0.34 m/s时不同网格的数值模拟变形与模型试验结果对比Fig.6 Comparison of deformed shape from numerical models with detailed and coarse mesh and physical model(current velocity of 0.34 m/s)
3.2 不同沉子重量下网箱的水动力
为了研究沉子的重量对于网箱的水动力的影响,本文对比Lader[2]的试验结果,计算不同沉子质量下的网箱的水动力。在3.1节计算了16×800 g沉子的情况,在这里显示的是其余两个配重的计算结果。
对比图6~8,可以看出,计算得到的阻力和升力随流速的变化趋势与试验结果是相同的,都是随着流速的增大而增大的。同时通过对比不同沉子下的阻力和升力的计算值与试验值结果,发现两者较为吻合。此外,随着流速的增大,计算结果相对实验的误差也是在逐渐增大的。在本文计算的几个工况中,最大的阻力和升力误差为沉子16×400 g且流速为0.56 m/s的情况(如图8所示),其与试验结果的相对误差分别为13.1%和10.7%。Kristiansen[2]曾对该试验进行了误差分析:由于渔网具有吸水的特性,使得试验时的渔网直径相对实际直径较小。同时,该试验中的沉子在测量水中的质量时也存在一定的误差。所以,由于试验存在一定不确定性因素可能使得计算结果较试验结果存在一定的误差。
3.3 不同流速下网箱的容积变化规律研究
为了研究流速对于网箱容积的影响,本文首先根据静止状态下的网衣各节点坐标,利用公式(20)计算出网箱初始容积。为了更加方便的导出计算结果,本文基于Python语言,编写了可以直接将ABAQUS结果导出的命令流,使用这一方法将稳定时刻网衣上各个节点的位移导出,再加上网衣初始时刻的节点坐标,即可得到网箱各个节点的位置。在水流作用下由于没有相关的网箱体积的相关试验结果,本文对比的是Moe[12]的计算结果,如图9所示。


图7 网箱试验和计算的阻力和升力结果对比图(16×600 g)Fig.7 Comparisons of drag force and lift force between model tests and calculated result in numerical analysis(16×600 g)图8 网箱试验和计算的阻力和升力结果对比图(16×400 g)Fig.8 Comparisons of drag force and lift force between model tests and calculated result in numerical analysis(16×400 g)图9 不同沉子重量下的网箱相对容积随流速变化情况Fig.9 Relative volume in net cage under different weight sinker corresponding to current velocity
在图9中,本文计算的网箱是没有网箱底部的,所以在计算时只计算了网箱网衣围住的部分,这一点与试验[5]和Moe[12]的计算模型是一致的。网箱的初始体积是根据网箱上各个点的初始坐标计算出来,使用的是32×12的网格。可以看出,随着流速的增大,网箱的体积是呈递减的趋势。当流速增大到0.5 m/s时,网箱的体积减少了约50%。此外,还可以明显地看到,网箱的容积与流速之间是非线性关系。
4 结论
本文基于ABAQUS的二次开发技术对网箱在水流作用下的受力进行了数值模拟。在计算中,本文使用子程序编译了基于网平面方法的水动力模型,并与试验结果进行了比较。研究结果显示,网衣的升力和阻力均随着流速的增大而增大,且计算与试验结果的最大相对误差为10.8%。而网箱的容积是随着流速的增大而减小的,在本文计算的模型中,当流速达到0.5 m/s时网箱的容积减小了约50%。网箱容积的计算结果与Moe[12]的基本一致。所以,通过本文的计算结果与试验结果对比可以看出,该方法可以应用于的网衣在水流作用下的数值模拟。
目前,该方法主要的研究对象是水流作用下的网箱的受力以及网箱体积的变化情况,未来该方法还可用于计算海洋柔性结构物中需自定义水动力载荷的情况。

