巧归纳 善解题

夏雪峰

平行四边形是中考必考内容之一，其考查形式丰富多样。解决这类题型时，我们需要运用平行四边形的性质——平行四边形的对边平行且相等、对角线互相平分得到底和高的关系，进而解决相关问题。

例（2018·陕西）如图1，点O是平行四边形ABCD的对称中心，AD＞AB，E、F分别是AB边上的点，且AB；G、H分别是BC边上的点，若S1、S2分别表示△EOF、△GOH的面积，则S1、S2之间的等量关系是______________。

【分析与解答】如图2，连接OA、OB、OC，可得且△EOF和△AOB同高，由

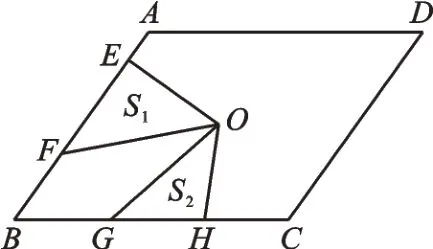
图1

图2

【归纳】平行四边形的知识点中有关面积问题常需要用到以下两个结论（基本图形）：

①平行四边形的一条对角线把平行四边形分成面积相等的两个三角形；

②平行四边形的两条对角线把平行四边形分成面积相等的四个小三角形。

跟踪练习：

1.如图3，在平行四边形ABCD中，AB和CD被五等分，AD和BC被三等分，已知阴影部分面积是1，则平行四边形ABCD的面积是___________。

2.如图4，过平行四边形ABCD对角线BD上一点M分别作两边的平行线EF与GH，则四边形AEMG的面积S1与四边形CFMH的面积S2的关系是___________。

图3

【答案】1.设每个小平行四边形面积为x，则S△DD2C4+S△BB2A4=2x，S△AD2A4+S△CB2C4=4x，S▱ABCD=15x，故而S阴影=15x-2x-4x=9x=1，则

2.由“平行四边形的一条对角线把平行四边形分成面积相等的两个三角形”得S△ABD=S△CBD、S△EBM=S△HBM、S△GDM=S△FDM，从而S△ABD-S△EBM-S△GDM=S△CBD-S△HBM-S△FDM，故而S1=S2。

通过以上几个练习我们可以发现，只要把复杂的图形转化为熟悉的基本图形，就能使复杂问题简单化。在解决与平行四边形有关的面积问题时，常会用到以上两个基本图形。我们往往通过添画辅助线，将所要求解的问题转化为基本图形来解决。